Analysis of uncertainty measure using unified hybrid censored data with applications

Abstract

Entropy is a measure of random variable uncertainty that reflects the anticipated quantity of information. In this paper, estimation of Shannon entropy for Lomax distribution, viz unified hybrid censored data are considered. The processes of maximum likelihood and Bayesian estimation procedures are regarded. The Bayesian estimator under balanced squared error, balanced linear exponential, and balanced general entropy loss functions are derived. The purpose of a Monte Carlo simulation study is designed to compare the accuracy of different estimators in the context of specific measures. Real data analysis is employed to confirm the proposed estimators. In summary, we discovered that, according to the findings of the study, the mean squared errors values decrease as the sample size increases. In the majority of cases, Bayesian estimates under balanced linear exponential loss function are more appropriate in terms of simulation out comes than other specified loss functions.

Keywords:

• Shannon entropy
• balanced linear exponential loss function
• Bayesian estimate
• Markov chain Monte Carlo method

1. Introduction

Due to a lack of funding and time constraints in the majority of life's trials, it is better to stop the test before all of the items fail. Censored samples are the observations that arise from that situation, and there are numerous censoring strategies. The most common types of censorship are type I (T-I) and type II (T-II). The test is completed at a predetermined censoring time in T-I censoring. The test is completed at a fixed number of failures in T-II censorship. The hybrid censoring scheme (HCS) is a combination of T-I and T-II censoring methods that can be characterized as below.

In a life-testing setting, assume there are n identical items with lifetimes are identically distributed and independent. Let $X_{1:n},X_{2:n},\dots ,X_{n:n}$ be the ordered failure times of these objects. When a prefixed number of items, $1\le r\le n$, out of n, fail, or when a prefixed period $T\in (0,\mathrm{\infty })$ is reached, the test is ended. Epstein [1] was the first to propose this hybrid censoring method, and there are two types: T-I HCS and T-II HCS.

The life-testing experiment in T-I HCS is completed at a random time $T_1^{\ast }=min(x_{r:n},T)$. The disadvantage of T-I HCS is that very few failures occur until the predetermined period $T_1^{\ast }$. To address this flaw, Childs et al. [2] suggested a recently HCS known as T-II HCS, which ensures fixed number of failures and has a termination time $T_2^{\ast }=max(x_{r:n},T)$. Although the T-II HCS ensures a specific amount of failures, detecting failures and completing the life test can take a lengthy time, which is a disadvantage. These techniques were modified by Chandrasekar et al. [3], who introduced generalized T-I HCS (GT-I HCS) and generalized T-II HCS (GT-II HCS).

One fixes $k,r\in (1,2,\dots ,n)$ and time $T\in (0,\mathrm{\infty })$ in GT-I HCS, where $k<r$. $T^{\ast }=min(x_{r:n},T)$, if the $k\mathrm{t}\mathrm{h}$ failure appears before the time T. $T^{\ast }=x_{k:n}$ if the $k\mathrm{t}\mathrm{h}$ failure occurs after the time T. In GT- II HCS, $r\in (1,2,\dots .,n)$ and $T_1,T_2\in (0,\mathrm{\infty })$ are chosen so that $T_1<T_2$. $T^{\ast }=T_1$ if the $r\mathrm{t}\mathrm{h}$ failure occurs before time $T_1$; $T^{\ast }=X_{r:n}$ if there is the $r\mathrm{t}\mathrm{h}$ failure between $T_1$ and $T_2$; otherwise, $T^{\ast }=T_2$. Even while these two new censored sampling systems outperform the previous ones, they nevertheless have flaws. Because there is just one the pre-assigned period T in GT-I HCS, we cannot ensure r failures. There is a chance that the GT-II HCS will not see a few failures until a pre-determined time $T_2$, and so it will have the same trouble as the T-I HCS. To overcome the shortcomings of both systems, Balakrishnan et al. [4] proposed a scheme that combines GT-I HCS and GT-II HCS and is referred to the unified hybrid censoring scheme (UHCS).

Fix the integers $r,k\in \left(1,2,\dots ,n\right)$ and the time points $T_1,T_2\in (0,\mathrm{\infty })$ in this scheme. $T^{\ast }=min(max(x_{r:n},T_1),T_2)$, if the kth failure happened prior to time $T_1$. $T^{\ast }=min(x_{r:n},T_2)$ if the kth failure happens between $T_1$ and $T_2$, and $T^{\ast }=x_{k:n}$, if the kth failure happens after $T_2$. 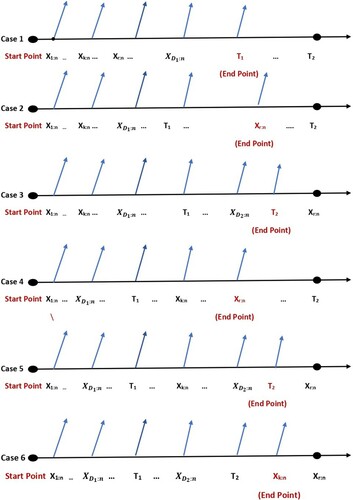Using this scheme strategy, we can confirm that the test will be finished in time $T_2$ with at least k failures, if not, exactly k failures. See [5] for more details on how well the difficulties in the previous types were resolved in this manner. As a result, we have the six cases indicated in Figure 1 under this UHCS:

Figure 1. Unified hybrid censoring scheme.

Case 1: $0<x_{k:n}<x_{r:n}<T_1<T_2$, if this is the case, we will end at $T_1$,

Case 2: $0<x_{k:n}<T_1<x_{r:n}<T_2$, if this is the case, we will end at $x_{r:n}$,

Case 3: $0<x_{k,:n}<T_1<T_2<x_{r:n}$, if this is the case, we will end at $T_2$,

Case 4: $0<T_1<x_{k:n}<x_{r:n}<T_2$, if this is the case, we will end at $x_{r:n}$,

Case 5: $0<T_1<x_{k:n}<T_2<x_{r:n}$, if this is the case, we will end at $T_2$,

Case 6: $0<T_1<T_2<x_{k:n}<x_{r:n}$, if this is the case, we will end at $x_{k:n}$.

Entropy is a key concept in statistics and information theory, and it was first recommended in physics second law of thermodynamics. Shannon [6] re-defined it and introduced the idea of entropy into information theory to quantify information uncertainty. Cover and Thomas [7] built on Shannon's notion, defining differential entropy (or continuous entropy) of a continuous random variable X with probability density function $f\left(x\right)$ as follows: (1) $H\left(f\right)=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f\left(x\right)\log f\left(x\right)\mathrm{d}x.$(1) Entropy measurement is a crucial concept in a variety of fields. More entropy indicates that there is less information in the sample.

Shannon entropy has many applications in many fields see [8,9] in physics and other fields can be found in [10–13].

Entropy in hybrid censoring data studied by Morabbi and Razmkhah [14]. In progressive censoring of T-II, Abo-Eleneen [15] looked at the entropy and the best method. Cho et al. [16] used doubly GT-II HCS to calculate the entropy of the Rayleigh distribution. Liu and Gui [17] investigated entropy estimate for the Lomax distribution using maximum likelihood (ML) and Bayesian methods under generalized progressively hybrid censoring. Under multiple censored data, Hassan and Zaky [18] found the ML estimator of Shannon entropy for the inverse Weibull distribution. The Shannon entropy of the inverse Weibull distribution under progressive first-failure censoring was investigated by Yu et al. [19]. Bantan et al. [20] investigated entropy estimation of inverse Lomax distribution viz multiple censored data.

The study of inference problems associated with entropy measures has recently gained prominence. As previously stated, the UHCS may be able to overcome the restrictions of the GT-I HCS and GT-II HCS. The Lomax distribution, on the other hand, it has sparked scholarly interest in the last decade due to its possible uses in a range of domains, including lifetime data prediction. We could not discover any study on the Shannon entropy measure estimation problem using UHCS in this regard. Consequently, the main purpose of this study is to use the UHCS to derive ML and Bayesian estimators from the Lomax distribution. Three losses are used to create a Bayesian estimator for Shannon entropy. The balanced-squared error loss (BSEL) function, balanced linear-exponential (BLINEX) loss function, and the balanced general entropy (BGE) loss function are used to create a Bayesian estimate for Shannon entropy. The Markov chain Monte Carlo (MCMC) strategy is employed to solve Bayesian entropy estimators with balanced loss functions. A numerical evaluation is used to assess the behaviour of the provided estimates via UHCS. Real data is analysed for more evidence, allowing the theoretical results to be confirmed.

This paper is planned as follows: The Shannon entropy for the Lomax distribution is calculated in Section 2. The ML Shannon entropy estimator is shown in Section 3. Section 4 covers the MCMC method for calculating Bayesian estimators and derives the Bayesian estimator of entropy under various loss functions. Simulation issue and application to real data are given in Sections 5 and 6, respectively. Section 7 brings the article to a close with some last thoughts.

2. Lomax distribution

Lomax (Lo) distribution is one of the important lifetime models. It has been useful in reliability and life testing problems (see, Hassan and Al-Ghamdi [21]). Lo distribution was first introduced by Lomax [22] and it is useful in a variety of domains, including actuarial science and economics. The Lo distribution was applied to income and wealth data see [23,24]. More details about applications of Lo distribution can found in [25,26].

A random variable $X$ is said to have Lo distribution with shape parameter α and scale parameter ϕ if its probability density function (pdf) is given by (2) $f\left(x\right)=\frac{\alpha }{\varphi }{[1+\frac{x}{\varphi }]}^{-(\alpha +1)},\alpha >0,\varphi >0,x\ge 0.$(2) The cumulative distribution function (cdf) of X is given by (3) $F\left(x\right)=1-{[1+\frac{x}{\varphi }]}^{-\alpha }.$(3) Various studies about Lo distribution can be found in the literature by several authors. Some recurrence relations between the moments of record values from the Lo distribution were studied by Balakrishnan and Ahsanullah [27]. On the basis of T-II censored data, Okasha [28] studied E-Bayesian estimate for the Lo distribution. Singh et al. [29] explored Bayesian estimation of Lo distribution under T-II HCS using Lindley's approximation. Statistical inference of Lo distribution using some information measures can be found in [30–32].

Substituting (2(2) $f\left(x\right)=\frac{\alpha }{\varphi }{[1+\frac{x}{\varphi }]}^{-(\alpha +1)},\alpha >0,\varphi >0,x\ge 0.$(2) ) into (1(1) $H\left(f\right)=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f\left(x\right)\log f\left(x\right)\mathrm{d}x.$(1) ) will give the Shannon entropy of the Lo distribution $\begin{array}{rl}H\left(x\right)& =-{\int }_0^{\mathrm{\infty }}\left(\alpha /\varphi \right){(1+\frac{x}{\varphi })}^{-(\alpha +1)}\\ & \times \log \left[\alpha \frac{1}{\varphi }{(1+\frac{x}{\varphi })}^{-(\alpha +1)}\right]\mathrm{d}x.\\ & =-{\int }_0^{\mathrm{\infty }}\left(\alpha /\varphi \right){(1+\frac{x}{\varphi })}^{-(\alpha +1)}\\ & \times [\log \left(\alpha \frac{1}{\varphi }\right)-(\alpha +1)\log (1+\frac{x}{\varphi })]\mathrm{d}x.\end{array}$Hence, (4) $H\left(x\right)=I_1+I_2.$(4) To compute H(x) in (4(4) $H\left(x\right)=I_1+I_2.$(4) ), we must calculate $I_1$ and $I_2$ $I_1=-{\int }_0^{\mathrm{\infty }}\frac{\alpha }{\varphi }{(1+\frac{x}{\varphi })}^{-(\alpha +1)}\log \left(\frac{\alpha }{\varphi }\right)\mathrm{d}x,$and $I_2={\int }_0^{\mathrm{\infty }}\alpha \frac{(\alpha +1)}{\varphi }{(1+\frac{x}{\varphi })}^{-(\alpha +1)}\log (1+\frac{x}{\varphi })\mathrm{d}x.$ Using integration rules we get (5) $\begin{array}{rl}{I}_1& =-\alpha \log \frac{\alpha }{\varphi }{\int }_0^{\mathrm{\infty }}\frac{1}{\varphi }{(1+\frac{x}{\varphi })}^{-(\alpha +1)}\mathrm{d}x\\ & =-\log \frac{\alpha }{\varphi }=\log \left(\varphi \right)-\log \left(\alpha \right).\end{array}$(5) To obtain $I_2$, let $u=1+\frac{x}{\varphi }$ then $du=\frac{dx}{\varphi }$, so $I_2$ will be $\begin{array}{rl}{I}_2& =\frac{\alpha (\alpha +1)}{\varphi }{\int }_1^{\mathrm{\infty }}(u{)}^{-(\alpha +1)}\log (u)\varphi \mathrm{d}u\\ & =\alpha (\alpha +1){\int }_1^{\mathrm{\infty }}(u{)}^{-(\alpha +1)}\log (u)\mathrm{d}u,\end{array}$then, using integration by parts we can find the value of the integral ${\int }_1^{\mathrm{\infty }}(u{)}^{-(\alpha +1)}\log (u)\mathrm{d}u=\frac{1}{{\alpha }^2},$then, (6) $I_2=\alpha (\alpha +1)\left(\frac{1}{{\alpha }^2}\right)=1+\frac{1}{\alpha }.$(6) As a result, the Shannon entropy of the Lo distribution looks like this: (7) $H\left(x\right)=\log \left(\varphi \right)-\log \left(\alpha \right)+\frac{1}{\alpha }+1.$(7) As a function of parameters α and ϕ, this is the needed formulation of Shannon entropy of the Lo distribution.

3. Maximum likelihood estimation

Under UHCS, the ML estimation of the Lo distribution is discussed in this section. Assume there are n identical items in a life-testing experiment. Let $X_{1:n},X_{2:n},\dots ,X_{n:n}$ represent the ordered failure times of these items, with fixed integer $r,k\in 1,2,\dots ,n$ where $k<r<n$ and time points $T_1,T_2\in (0,\mathrm{\infty })$ where $T_1<T_2$. Then the likelihood function of α and ϕ, for six cases of UHCS is given by (8) $L(\underset{\_}{x}|\alpha ,\varphi )=\frac{n!}{(n-D)!}\left[\prod _{i=1}^{D}f\right(x_{i:n}\left)\right][1-F(c){]}^{n-D},$(8) where D is total number of failures up to time c in the experiment, and its value in the statements given by (9) $(D,c)=\{\begin{array}{ll}(D_1,T_1)& \text{for case 1,}\\ (r,x_{r:n})& \text{for case 2 and 4,}\\ (D_2,T_2)& \text{for case 3 and 5,}\\ (k,x_{k:n})& \text{for case 6,}\end{array}$(9) where $D_1$ and $D_2$ refer to the number of failures prior to $T_1$ and $T_2$, respectively. Substituting (2(2) $f\left(x\right)=\frac{\alpha }{\varphi }{[1+\frac{x}{\varphi }]}^{-(\alpha +1)},\alpha >0,\varphi >0,x\ge 0.$(2) ) and (3(3) $F\left(x\right)=1-{[1+\frac{x}{\varphi }]}^{-\alpha }.$(3) ) in (8(8) $L(\underset{\_}{x}|\alpha ,\varphi )=\frac{n!}{(n-D)!}\left[\prod _{i=1}^{D}f\right(x_{i:n}\left)\right][1-F(c){]}^{n-D},$(8) ) we obtain $\begin{array}{rl}L(\underset{\_}{x}|\alpha ,\varphi )& =\frac{n!}{(n-D)!}\left[{\left(\frac{\alpha }{\varphi }\right)}^D\prod _{i=1}^D{(1+\frac{x_{i:n}}{\varphi })}^{-(\alpha +1)}\right]\\ & \times {[1-(1-{(1+\frac{c}{\varphi })}^{-\alpha })]}^{n-D},\end{array}$this equation can be written in the following way: (10) $\begin{array}{rl}L(\underset{\_}{x}|\alpha ,\phi )& =E{\left(\frac{\alpha }{\varphi }\right)}^D\frac{1}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\\ & \times e^{-\alpha [\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi }\left)\right]},\end{array}$(10) where $E=\frac{n!}{(n-D)!}$. Taking the logarithm of both sides we get (11) $\begin{array}{rl}l(\underset{\_}{x}|\alpha ,\varphi )& \propto D\log \left(\frac{\alpha }{\varphi }\right)-(\alpha +1)\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\varphi })\\ & -\alpha (n-D)\log (1+\frac{c}{\varphi }),\end{array}$(11) where $l(\underset{\_}{x}|\alpha ,\varphi )$ is the logarithm of the likelihood function. Taking derivatives of (11(11) $\begin{array}{rl}l(\underset{\_}{x}|\alpha ,\varphi )& \propto D\log \left(\frac{\alpha }{\varphi }\right)-(\alpha +1)\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\varphi })\\ & -\alpha (n-D)\log (1+\frac{c}{\varphi }),\end{array}$(11) ) with respect to α and ϕ, we can get (12) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\alpha }& =\frac{D}{\alpha }-\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\varphi })\\ & -(n-D)\log (1+\frac{c}{\varphi }),\end{array}$(12) and (13) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\varphi }& =-\frac{D}{\varphi }+(\alpha +1)\sum _{i=1}^D\frac{x_{i:n}}{{\varphi }^2(1+\frac{x_{i:n}}{\varphi })}\\ & +\frac{\alpha (n-D)c}{{\varphi }^2(1+\frac{c}{\varphi })}.\end{array}$(13) To find the ML estimator of α and ϕ, set Equations (12(12) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\alpha }& =\frac{D}{\alpha }-\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\varphi })\\ & -(n-D)\log (1+\frac{c}{\varphi }),\end{array}$(12) ) and (13(13) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\varphi }& =-\frac{D}{\varphi }+(\alpha +1)\sum _{i=1}^D\frac{x_{i:n}}{{\varphi }^2(1+\frac{x_{i:n}}{\varphi })}\\ & +\frac{\alpha (n-D)c}{{\varphi }^2(1+\frac{c}{\varphi })}.\end{array}$(13) ) equal to zero and solve them. Therefore, Equation (12(12) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\alpha }& =\frac{D}{\alpha }-\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\varphi })\\ & -(n-D)\log (1+\frac{c}{\varphi }),\end{array}$(12) ) can be written as (14) $\hat{\alpha }=A\left(\hat{\varphi }\right),$(14) where $A\left(\hat{\varphi }\right)=\frac{D}{\sum _{i=1}^D\log (1+\frac{x_{i:n}}{\hat{\varphi }})+(n-D)\log (1+\frac{c}{\hat{\varphi }})},$and Equation (13(13) $\begin{array}{rl}\frac{\mathrm{\partial }l(\underset{\_}{x}|\alpha ,\varphi )}{\mathrm{\partial }\varphi }& =-\frac{D}{\varphi }+(\alpha +1)\sum _{i=1}^D\frac{x_{i:n}}{{\varphi }^2(1+\frac{x_{i:n}}{\varphi })}\\ & +\frac{\alpha (n-D)c}{{\varphi }^2(1+\frac{c}{\varphi })}.\end{array}$(13) ) can be written as (15) $-\frac{D}{\hat{\varphi }}+(\hat{\alpha }+1)\sum _{i=1}^D\frac{x_{i:n}}{{\hat{\varphi }}^2(1+\frac{x_{i:n}}{\hat{\varphi }})}+\frac{\hat{\alpha }(n-D)c}{{\hat{\varphi }}^2(1+\frac{c}{\hat{\varphi }})}=0,$(15) substituting from Equation (14(14) $\hat{\alpha }=A\left(\hat{\varphi }\right),$(14) ) into (15(15) $-\frac{D}{\hat{\varphi }}+(\hat{\alpha }+1)\sum _{i=1}^D\frac{x_{i:n}}{{\hat{\varphi }}^2(1+\frac{x_{i:n}}{\hat{\varphi }})}+\frac{\hat{\alpha }(n-D)c}{{\hat{\varphi }}^2(1+\frac{c}{\hat{\varphi }})}=0,$(15) ) to calculate $\hat{\varphi }$ as shown (16) $\begin{array}{rl}& -\frac{D}{\hat{\varphi }}+\left(A\right(\hat{\varphi })+1)\sum _{i=1}^D\frac{x_{i:n}}{{\hat{\varphi }}^2(1+\frac{x_{i:n}}{\hat{\varphi }})}\\ & +\frac{A\left(\hat{\varphi }\right)(n-D)c}{{\hat{\varphi }}^2(1+\frac{c}{\hat{\varphi }})}=0.\end{array}$(16) Therefore, we can use an iterative procedure to compute the ML estimator of ϕ and then substitute into (14(14) $\hat{\alpha }=A\left(\hat{\varphi }\right),$(14) ) to find the ML estimator of α. Then we get the ML estimator of $H\left(x\right)$, indicated by $\hat{H}\left(x\right)$ as follows: (17) $\hat{H}\left(x\right)=\log \left(\hat{\varphi }\right)-\log \left(\hat{\alpha }\right)+\frac{1}{\hat{\alpha }}+1.$(17)

4. Bayesian estimation

Here, we find Bayesian estimators of the unknown parameters α, ϕ, and H(x) based on BSEL, BLINEX, and BGE loss functions. The gamma distribution is used as a conjugate prior for the class of distribution and is also a conjugate prior for Lomax distribution so we assume that α and ϕ are distributed independently as gamma ($a_1,b_1$) and gamma ($a_2,b_2$) priors, respectively. Then, the prior of α and ϕ is $\begin{array}{rl}& {\pi }_1\left(\alpha \right)\propto \left({\alpha }^{a_1-1}{e}^{-b_1\alpha }\right),\alpha >0,\\ & {\pi }_2\left(\varphi \right)\propto \left({\varphi }^{a_2-1}{e}^{-\varphi b_2}\right),\varphi >0.\end{array}$Where we assumed the hyperparameters $a_1,a_2,b_1$ and $b_2>0$ are constant and known. The joint prior density of α and ϕ is given by (18) $\pi (\alpha ,\varphi )\propto {\alpha }^{a_1-1}{\varphi }^{a_2-1}{e}^{-(b_1\alpha +b_2\varphi )}.$(18) The posterior distribution is given by (19) ${\pi }^{\ast }(\alpha ,\varphi |\underset{\_}{x})=\frac{L(\underset{\_}{x}|\alpha ,\varphi )\pi (\alpha ,\varphi )}{\int \int L(\underset{\_}{x}|\alpha ,\varphi )\pi (\alpha ,\varphi )\mathrm{d}\alpha \mathrm{d}\varphi },$(19) where $\pi (\alpha ,\varphi )$ is the joint prior distribution for the parameters α and ϕ, $L(\underset{\_}{x}|\alpha ,\varphi )$ is the likelihood function, and ${\pi }^{\ast }(\alpha ,\varphi |\underset{\_}{x})$ is the posterior distribution for the parameters.

From (10(10) $\begin{array}{rl}L(\underset{\_}{x}|\alpha ,\phi )& =E{\left(\frac{\alpha }{\varphi }\right)}^D\frac{1}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\\ & \times e^{-\alpha [\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi }\left)\right]},\end{array}$(10) ) and (18(18) $\pi (\alpha ,\varphi )\propto {\alpha }^{a_1-1}{\varphi }^{a_2-1}{e}^{-(b_1\alpha +b_2\varphi )}.$(18) ) we obtain the joint posterior density function as follows: (20) $\begin{array}{rl}{\pi }^{\ast }(\alpha ,\varphi |\underset{\_}{x})& =E_1{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }\\ & \times e^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}\\ & \times \frac{1}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })},\end{array}$(20) where $E_1$ is the normalizing constant given by (21) $E_1=\frac{1}{{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}L(\underset{\_}{x}|\alpha ,\varphi )\pi (\alpha ,\varphi )\mathrm{d}\alpha \mathrm{d}\varphi },$(21) then, (22) $\begin{array}{rl}& {\pi }^{\ast }(\alpha ,\varphi |\underset{\_}{x})\\ & \propto {\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }\\ & \times e^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}\\ & \times \frac{1}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}.\end{array}$(22) The marginal posterior distributions of α and ϕ take the following forms: (23) $\begin{array}{rl}& {\pi }_1^{\ast }\left(\alpha |\underset{\_}{x}\right)\\ & \propto {\alpha }^{D+a_1-1}{e}^{-\alpha b_1}{\int }_0^{\mathrm{\infty }}{\varphi }^{(a_2-D-1)}\\ & \times \frac{e^{-b_2\varphi +\alpha [\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi }\left)\right]}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\mathrm{d}\varphi ,\end{array}$(23) and (24) $\begin{array}{rl}{\pi }_2^{\ast }\left(\varphi |\underset{\_}{x}\right)& \propto \frac{{\varphi }^{(a_2-D-1)}{e}^{-b_2\varphi }}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}{\int }_0^{\mathrm{\infty }}{\alpha }^{D+a_1-1}\\ & \times e^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}\mathrm{d}\alpha .\end{array}$(24) It is obvious from (22(22) $\begin{array}{rl}& {\pi }^{\ast }(\alpha ,\varphi |\underset{\_}{x})\\ & \propto {\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }\\ & \times e^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}\\ & \times \frac{1}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}.\end{array}$(22) ) that the posterior density function of α given ϕ is proportional to (25) $\begin{array}{rl}& {\pi }_1^{\ast }\left(\alpha |\varphi \right)\\ & \propto {\alpha }^{D+a_1-1}{e}^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}.\end{array}$(25) As a result, the posterior density function of α given ϕ is gamma distribution with shape parameter $(D+a_1)$ and scale parameter $[b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]$. Consequently, samples of α can be easily created using any gamma generating routine.

It is possible to write the posterior density function of ϕ given α as follows: (26) $\begin{array}{rl}& {\pi }_2^{\ast }\left(\varphi |\alpha \right)\\ & \propto \frac{{\varphi }^{(a_2-D-1)}{e}^{-b_2\varphi +\alpha [\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi }\left)\right]}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}.\end{array}$(26) Because this equation cannot be reduced analytically to well-known distributions, standard sampling methods cannot be used to sample directly. Using the MCMC method to get estimator under the following balanced loss functions.

4.1. Loss functions

Loss functions are classified according to symmetry criteria into two main types: the first one is a symmetric loss functions such as the squared error loss function. The second type of loss functions is called asymmetric loss functions, one of these functions is the entropy loss function and two types called unbalanced loss function. Balanced loss functions are appealing as they combine proximity of a given estimator δ to both a target estimator ${\delta }_o$ and the unknown parameter θ which is being estimated see [33] and is defined according to Zellner's formula as follows: (27) $L_{\rho ,\omega ,\delta o}(\theta ,\rho )=\omega \rho (\delta ,\delta o)+(1-\omega )\rho (\theta ,\delta ),$(27) where $0\le \omega \le 1$ is a weighted coefficient, $\rho (\theta ,\delta )$ is an arbitrary loss function, $\delta o$ is a chosen prior estimator of θ, and $\rho (\delta ,\delta o)$ an unbalanced loss function for the likelihood function. When $\omega =0$ there are no differences between Bayesian estimators under the balanced and unbalanced loss functions.

In the BSEL loss function $\rho (\theta ,\delta )=(\delta -\theta {)}^2$, then (27(27) $L_{\rho ,\omega ,\delta o}(\theta ,\rho )=\omega \rho (\delta ,\delta o)+(1-\omega )\rho (\theta ,\delta ),$(27) ) takes the form $L_{\rho ,\omega ,\delta o}=\omega (\delta -\delta o{)}^2+(1-\omega \left)\right(\delta -\theta {)}^2,$and the Bayesian estimator of H(x) in this case is given by (28) $\begin{array}{rl}{H}_{BS}\left(\underset{\_}{x}\right)& =\omega \hat{H}\left(x\right)+(1-\omega )E\left(H\right(x\left)|\underset{\_}{x}\right).\end{array}$(28) (29) $\begin{array}{rl}{H}_{BS}\left(\underset{\_}{x}\right)& =\omega \hat{H}\left(x\right)+E_1(1-\omega ){\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}H\left(x\right)\\ & \times \frac{{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }{e}^{-\alpha Y}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\mathrm{d}\alpha \mathrm{d}\varphi ,\end{array}$(29) where $\begin{array}{rl}Y& =(b_1+[\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })\\ & +(n-D)\ln (1+\frac{c}{\varphi })\phantom{\sum _{i=1}^D}])\end{array}$and $E_1$ is the normalizing constant given in (21(21) $E_1=\frac{1}{{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}L(\underset{\_}{x}|\alpha ,\varphi )\pi (\alpha ,\varphi )\mathrm{d}\alpha \mathrm{d}\varphi },$(21) ).

If we choose $\rho (\theta ,\delta )=e^{q(\delta -\delta o)}-q(\delta -\theta )-1,$we will get the BLINEX loss function where q represents the shape parameter of the loss function and the behaviour of the BLINEX loss function and BGE loss function changes with the choice of q. Then the Bayesian estimator of $H\left(x\right)$ in this case is (30) $\begin{array}{rl}{H}_{BL}\left(\underset{\_}{x}\right)& =\frac{-1}{q}\ln [\omega e^{-q\delta o}+(1-\omega \left)E\right(e^{-q\theta }|\underset{\_}{x}\left)\right],\\ & =\frac{-1}{q}\ln [\phantom{\frac{e^{-qH\left(x\right)-b_2\varphi -\alpha Y}{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}}{\sum _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}}\omega e^{-qH\left(x\right)}+E_1(1-\omega ){\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\\ & \times \frac{e^{-qH\left(x\right)-b_2\varphi -\alpha Y}{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\mathrm{d}\alpha \mathrm{d}\varphi ].\end{array}$(30) If we choose $\rho (\delta ,\theta )={\left(\frac{\delta o}{\theta }\right)}^{-q}-1-q\ln \left(\frac{\delta o}{\theta }\right),$we will get the BGE loss function where $q\ne 0$, and the Bayesian estimator of $H\left(x\right)$ in this case is (31) $\begin{array}{rl}& H_{BG}\left(\underset{\_}{x}\right)\\ & =\left[\phantom{\frac{\left(H\right(x){)}^{-q}{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }{e}^{-\alpha Y}}{\sum _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}}\omega \right(H(x{)}^{-q}+E_1(1-\omega ){\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\left(H\right(x){)}^{-q}\\ & \times {\frac{{\alpha }^{D+a_1-1}{\varphi }^{a_2-D-1}{e}^{-b_2\varphi }{e}^{-\alpha Y}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}\mathrm{d}\alpha \mathrm{d}\varphi ]}^{\frac{-1}{q}}.\end{array}$(31)

4.2. MCMC approach

The MCMC method is used to generate samples from posterior distributions and then compute Bayesian Shannon entropy estimators under balanced loss functions. MCMC schemes come in a wide range of options. Gibbs sampling and more general Metropolis-within-Gibbs samplers are a significant subclass of MCMC methods.

To pull samples from posterior density functions and then compute Bayesian estimators, we suggest the following MCMC technique.

Algorithm

1. ${\varphi }_0=\hat{\varphi }$.

2. Set $l=1$.

3. ${\alpha }^{\left(l\right)}$ is obtained from Gamma ${\pi }_1^{\ast }\left(\alpha |\varphi \right)$.

4. To generate ${\varphi }^{\left(l\right)}$ from ${\pi }_2^{\ast }\left(\varphi |\alpha \right)$ using Metropolis–Hastings, see Metropolis et al. [34].

5. Calculate ${\alpha }^{\left(t\right)}$ and ${\varphi }^{\left(t\right)}$.

6. Steps 2–5 should be repeated N times.

7. Obtain the Bayesian estimators of α and ϕ and compute the entropy function H(x) with respect to the balanced loss functions.

5. Simulation study

In this section, we present some simulation results mainly to compare the performances of the ML estimate (MLE) and Bayesian estimate (BE) of the Shannon entropy for Lo distribution under different losses, in terms of mean squared errors (MSEs).

1. For given hyperparameters $a_1,b_1,a_2$ and $b_2$ generate random values of α and ϕ from Equations (25(25) $\begin{array}{rl}& {\pi }_1^{\ast }\left(\alpha |\varphi \right)\\ & \propto {\alpha }^{D+a_1-1}{e}^{-\alpha [b_1+(\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi })\left)\right]}.\end{array}$(25) ) and (26(26) $\begin{array}{rl}& {\pi }_2^{\ast }\left(\varphi |\alpha \right)\\ & \propto \frac{{\varphi }^{(a_2-D-1)}{e}^{-b_2\varphi +\alpha [\sum _{i=1}^D\ln (1+\frac{x_{i:n}}{\varphi })+(n-D)\ln (1+\frac{c}{\varphi }\left)\right]}}{\prod _{i=1}^D(1+\frac{x_{i:n}}{\varphi })}.\end{array}$(26) ).

2. For given values of n and D with the initial values of α and ϕ given in Step 1, we generate random samples from the inverse cdf of Lo distribution and then ordered them.

3. The MLE of $H\left(x\right)$ were calculated for certain values of r, k, $T_1$ and $T_2$ under six cases of UHCS, as explained in Section 3.

4. The BE of $H\left(x\right)$ based on BSEL, BLINEX, and BGE loss functions using the MCMC method has been given, respectively, for specific values of r, k, $T_1$ and $T_2$, as discussed in Section 4.

5. If $\hat{\theta }$ is an estimate of θ then MSE over N samples, where $i=1,2,\dots ,N$, is calculated as follows based on sample j, where j = 1, 2,…,N, then MSE over N samples is given by (32) $MSE\left(\hat{\theta }\right)=\sum _{i=1}^N\frac{(\hat{\theta }-\theta {)}^2}{N},\hat{\theta }=(\hat{\alpha },\hat{\varphi }).$(32)

6. Steps $1-5$ are repeated where, $N=1000$ times and used 11,000 MCMC sample and discard the first 1000 values as “burn-in” and generated a sample from Lo distribution with fixed hyperparameters equals $a_1=2,b_1=0.5,a_2=1.7$ and $b_2=1.5$, weighted coefficient $\omega =0.5$ and the values of $q=-0.5,0.5$. The estimate studied under two cases ($\alpha =1.2,\varphi =0.55,H_0\left(x\right)=1.053$), and ($\alpha =0.9,\varphi =3.55,H_0\left(x\right)=3.48342$) and two sample sizes where the first sample $n=60,r=50,k=(20,30,40)$, the second sample $n=100,r=80,k=(40,50,65,75)$, values of $T_1$ and $T_2$ are selected as ($T_1=1.8,T_2=2.4$), ($T_1=2.1,T_2=5$), ($T_1=3,T_2=5$) and ($T_1=3,T_2=8$). In each case the estimation of the Shannon entropy (in the first row) and MSE (in the next row) for all cases are calculated as shown in Tables 1 and 2.

Table 1. MLE and Bayesian estimate of Shannon entropy based on UHCS under balanced loss functions ($\alpha =1.2,\varphi =0.55,H_0\left(x\right)=1.053$) and $\omega =0.5$ and MSE of all estimates.

				$(T_1=1.8$ $T_2=2.4)$
n	r	k	MLE	BSLE	BLINEX		BGE
					$(-0.5)$	$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$
60	50	20	1.04716	1.16646	1.17619	1.15713	1.15745	1.14036
			0.05833	0.05533	0.05565	0.05587	0.05604	0.05811
		30	1.0387	1.15659	1.16622	1.14736	1.14781	1.13115
			0.0564	0.0526	0.05316	0.05434	0.05301	0.05454
		40	0.99326	1.14227	1.15264	1.13234	1.13231	1.11366
			0.0533	0.04838	0.04828	0.04877	0.04983	0.05339
100	80	40	1.1271	1.12154	1.13014	1.19317	1.19319	1.1171
			0.04984	0.02984	0.02941	0.03046	0.03088	0.0335
		50	1.01844	1.11918	1.12642	1.1212	1.11223	1.09881
			0.04624	0.02891	0.0288	0.02918	0.02959	0.03138
		65	1.0129	1.11683	1.12434	1.10953	1.10964	1.09578
			0.03914	0.02719	0.02708	0.02748	0.02787	0.02975
		75	0.998	1.11026	1.11754	1.10318	1.10344	1.09029
			0.03184	0.01929	0.0193	0.01943	0.01968	0.02086
					$(T_1=2.1$	$T_2=5)$
60	50	20	1.0375	1.17586	1.18616	1.16598	1.16592	1.14735
			0.0692	0.05912	0.05945	0.0596	0.06048	0.06427
		30	1.03401	1.17171	1.18155	1.16228	1.16274	1.14571
			0.0652	0.05232	0.05207	0.05286	0.05271	0.05425
		40	1.01297	1.15334	1.16331	1.14378	1.14406	1.12644
			0.0622	0.05084	0.05095	0.05101	0.05165	0.05394
100	80	40	1.1138	1.14589	1.15323	1.13873	1.13867	1.1947
			0.04531	0.03812	0.0377	0.0387	0.04914	0.05165
		50	1.01844	1.13537	1.14306	1.1279	1.12819	1.11431
			0.04131	0.03774	0.03186	0.0328	0.03812	0.03934
		65	0.97334	1.09361	1.10193	1.08551	1.08552	1.06988
			0.03521	0.02812	0.0277	0.0297	0.02914	0.02965
		75	0.92248	1.10219	1.10948	1.09509	1.09523	1.08179
			0.03121	0.02774	0.02776	0.02988	0.02812	0.02934
				$(T_1=3$  $T_2=5)$
n	r	k	MLE	BSLE	BLINEX		BGE
					$(-0.5)$	$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$
60	50	20	1.03694	1.17464	1.18438	1.1653	1.16556	1.14846
			0.0666	0.05726	0.0578	0.05802	0.05803	0.06025
		30	1.01893	1.16114	1.17114	1.15154	1.15195	1.13453
			0.0632	0.05062	0.05103	0.05252	0.05115	0.05294
		40	1.0154	1.16142	1.17146	1.15179	1.15199	1.13416
			0.0611	0.04764	0.04789	0.04973	0.04856	0.05134
100	80	40	1.10269	1.13407	1.1422	1.13605	1.13607	1.19062
			0.0374	0.031	0.03961	0.0457	0.03198	0.03393
		50	1.01969	1.12265	1.13	1.11549	1.11556	1.10187
			0.0324	0.0308	0.03063	0.03112	0.03154	0.03353
		65	1.0119	1.11764	1.12493	1.11054	1.11071	1.09733
			0.0224	0.02701	0.02692	0.02723	0.02757	0.0291
		75	1.01005	1.11771	1.12527	1.11034	1.11049	1.09656
			0.0214	0.02771	0.02657	0.02699	0.02737	0.0286
					$(T_1=3$	$T_2=8)$
60	50	20	1.16436	1.16715	1.17599	1.1587	1.15945	1.14482
			0.05917	0.05417	0.05525	0.05332	0.05387	0.05475
		30	1.08436	1.13265	1.14346	1.12229	1.12262	1.10357
			0.0531	0.0398	0.03992	0.04005	0.04059	0.04308
		40	1.03472	1.11487	1.11532	1.10485	1.11512	1.01665
			0.044	0.0317	0.03188	0.03281	0.0388	0.04311
100	80	40	1.01475	1.12811	1.13552	1.1209	1.12103	1.10739
			0.0336	0.02833	0.02824	0.02857	0.02899	0.03073
		50	1.0117	1.11406	1.12201	1.10633	1.10654	1.09206
			0.0314	0.02714	0.02703	0.02742	0.02773	0.02936
		65	1.0028	1.00268	1.00986	1.00568	1.10109	1.1011
			0.0236	0.02417	0.02451	0.02497	0.0252	0.0256
		75	0.97503	1.08964	1.0974	1.0821	1.08208	1.06749
			0.0221	0.02339	0.02298	0.02395	0.0244	0.02694

Table 2. MLE and Bayesian estimate of Shannon entropy based on UHCS under balanced loss functions ($\alpha =0.9,\varphi =3.55,H_0\left(x\right)=3.48342$) and $\omega =0.5$ and MSE of all estimates.

				$(T_1=1.8$ $T_2=2.4)$
n	r	k	MLE	BSLE	BLINEX		BGE
					$(-0.5)$	$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$
60	50	20	3.42778	3.36145	3.36696	3.35573	3.35975	3.35628
			0.11347	0.10306	0.10218	0.10398	0.10349	0.10439
		30	3.44387	3.37546	3.38088	3.36981	3.37379	3.37039
			0.10045	0.09206	0.09147	0.0927	0.09239	0.09306
		40	3.45732	3.38604	3.39152	3.38033	3.38438	3.38099
			0.10005	0.09156	0.09135	0.0918	0.0917	0.092
100	80	40	3.43191	3.33119	3.33658	3.32558	3.32953	3.32613
			0.08041	0.08393	0.08297	0.08498	0.0843	0.08507
		50	3.45027	3.34688	3.35237	3.34116	3.34519	3.34172
			0.07594	0.07743	0.07647	0.07847	0.07783	0.07866
		65	3.44844	3.34463	3.35007	3.33895	3.34296	3.33955
			0.07493	0.07529	0.07453	0.07614	0.07559	0.07621
		75	3.43518	3.33554	3.34126	3.3296	3.33372	3.33003
			0.07377	0.07039	0.06859	0.07233	0.07117	0.07278
					$(T_1=2.1$	$T_2=5)$
60	50	20	3.4438	3.37482	3.38032	3.36909	3.37313	3.3697
			0.10963	0.10033	0.12984	0.10087	0.10062	0.10122
		30	3.45326	3.3831	3.38864	3.37733	3.38141	3.37796
			0.10847	0.09807	0.09967	0.09852	0.09834	0.09888
		40	3.43661	3.36885	3.37442	3.36305	3.36711	3.36357
			0.10483	0.09572	0.09471	0.09683	0.09623	0.09729
100	80	40	3.44302	3.34062	3.34606	3.33495	3.33894	3.33551
			0.09694	0.08322	0.0823	0.08422	0.08358	0.08433
		50	3.43337	3.33447	3.33978	3.32893	3.33283	3.32948
			0.08528	0.08145	0.07986	0.08318	0.08215	0.0836
		65	3.43657	3.33684	3.34244	3.33101	3.33506	3.33146
			0.08317	0.07869	0.07764	0.07986	0.07914	0.08009
		75	3.44776	3.34591	3.35145	3.34013	3.34419	3.34068
			0.08217	0.07709	0.07612	0.07916	0.0785	0.07933
				$(T_1=3$ $T_2=5)$
n	r	k	MLE	BSLE	BLINEX		BGE
					$(-0.5)$	$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$
60	50	20	3.45935	3.37438	3.38013	3.36842	3.37257	3.36889
			0.11287	0.10342	0.10237	0.10456	0.10394	0.105
		30	3.42156	3.35783	3.36345	3.35201	3.35609	3.35253
			0.10641	0.10261	0.10228	0.10298	0.10284	0.10332
		40	3.45246	3.38306	3.3886	3.37729	3.38137	3.37793
			0.10341	0.10218	0.10092	0.10152	0.10267	0.10228
100	80	40	3.44776	3.34565	3.3511	3.33997	3.34397	3.34053
			0.07687	0.07775	0.07679	0.07882	0.07816	0.079
		50	3.42886	3.32859	3.33406	3.3229	3.32688	3.3234
			0.07585	0.07638	0.07509	0.0767	0.0769	0.0788
		65	3.45399	3.35033	3.35585	3.34457	3.34862	3.34515
			0.07442	0.07386	0.073	0.07582	0.07423	0.07598
		75	3.44895	3.34613	3.35175	3.34027	3.34437	3.3408
			0.07134	0.06963	0.07145	0.07392	0.07215	0.07324
					$(T_1=3$	$T_2=8)$
60	50	20	3.42627	3.35906	3.36471	3.35318	3.35731	3.35374
			0.12587	0.11397	0.11311	0.1149	0.11443	0.11537
		30	3.41264	3.34484	3.34039	3.33906	3.34313	3.35396
			0.10809	0.10357	0.10233	0.10488	0.1042	0.10452
		40	3.42963	3.3653	3.37093	3.35946	3.36353	3.35994
			0.1057	0.09971	0.09902	0.10048	0.10006	0.10079
100	80	40	3.44236	3.33474	3.34018	3.32907	3.32307	3.31966
			0.0718	0.0745	0.07368	0.07541	0.07482	0.07547
		50	3.41426	3.31006	3.32548	3.3144	3.3184	3.315
			0.06946	0.07243	0.07165	0.0733	0.07273	0.07335
		65	3.43116	3.32954	3.33483	3.32403	3.32791	3.32458
			0.06094	0.06691	0.06599	0.06792	0.06725	0.06796
		75	3.43077	3.32984	3.33535	3.32411	3.32813	3.32466
			0.05274	0.06307	0.06047	0.06117	0.0605	0.06141

Simulated results:

Here are some observations on the Shannon entropy estimates performance as shown in Tables 1 and 2.

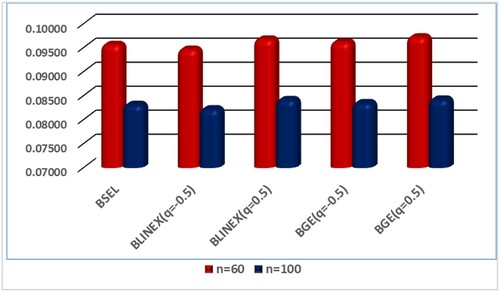
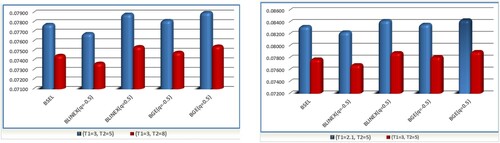
• The MSE of MLE and BE of the Shannon entropy decrease when n is increased (Figure 2).

• The Bayes estimate of $H_{BLINEX}\left(x\right)$ at $q=-0.5$ is superior than the other Bayes estimates for different values of n in terms of yielding more information as seen in Figure 3. However, when compared to other Bayes estimates, the Bayes estimate of $H_{BGE}\left(x\right)$ at $q=0.5$ is the worst, resulting in less information.

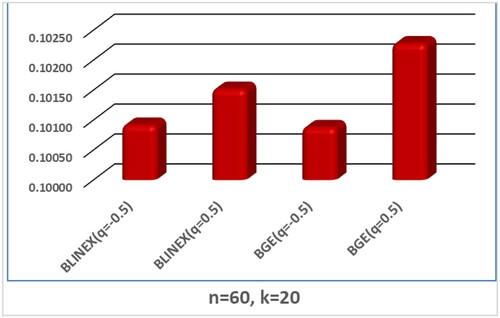
• Figure 3 illustrates that for $q=-0.5$, the Bayes estimate of $H_{BLINEX}\left(x\right)$ and $H_{BGE}\left(x\right)$ is chosen over the others, allowing for better information.

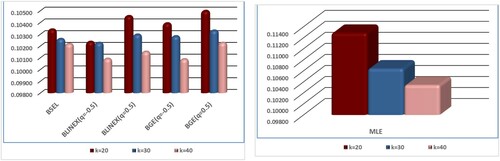
• The Bayes estimate of $H_{BLINEX}\left(x\right)$ at $q=-0.5$ for $n=60$, are favoured over the others for different values of k. The Bayes estimate of $H_{BGE}\left(x\right)$ at $q=0.5$, on the other hand, is the poorest for various values of k. The MSE of $H\left(x\right)$ in MLE decreases when the value of k increases (refer Figure 4).

• Figure 5 indicates that the Bayes estimate of $H_{BLINEX}\left(x\right)$ at $q=-0.5$ is favoured over the others, for selected values of $T_1$ and $T_2$ in terms of least MSE, resulting in reduced variability.

• The amount of data obtained in the Bayesian estimate are larger than at MLE because the uncertainty in case of BE is less than the uncertainty in MLE.

• The Shannon entropy BEs drop as $T_2$ is increased for fixed $n,r,k$ and $T_1$. In addition, for fixed $n,r,k$ and $T_2$, the BE of Shannon entropy decreases by increasing $T_1$ in the majority of cases.

• Whenever $T_1$ or $T_2$ is small, the Bayes estimator being better for selected values of $n,r$ and k in terms of least MSE.

• A greater amount of data are obtained when the sample size is large because there is a small uncertainty at it.

Figure 2. The MSE of Shannon entropy estimation for different values of sample size.

Figure 3. The MSE of Shannon entropy BEs based on BLINEX and BGE loss functions.

Figure 4. The MSE of Shannon entropy estimation under different values of k at n = 60.

Figure 5. The MSE of Shannon entropy estimates at ($T_1=2.1$ and $T_2=5$), ($T_1=3$ and $T_2=5$) and ($T_1=3$ and $T_2=8$) for $n=100,k=40$.

Figure 6. MCMC plots at $n=100,T_1=3,T_2=8,m=65,r=80$.

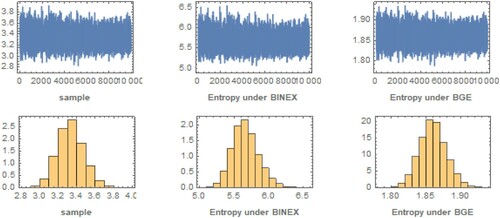
Figures 6 and 7 display a trace plot of the Shannon entropy for different loss functions with iteration numbers (1000) for $n=100,T_1=3,T_2=8,m=65,$ and $r=80$ and for $n=100,T_1=3,T_2=8,m=20,r=50$, respectively. The estimations show that all of the generated posteriors fit the theoretical posterior density functions very well, and it is clear that a large MCMC loop produces similar and more efficient outcomes. These plots resemble a horizontal band with no long upward or downward trends, which are convergence markers.

Figure 7. MCMC plots at $n=60,T_1=3,T_2=8,m=20,r=50$.

6. Real life data

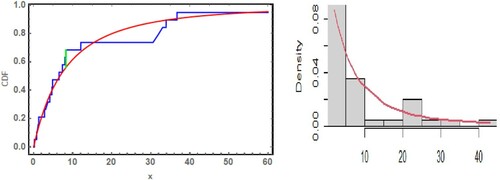
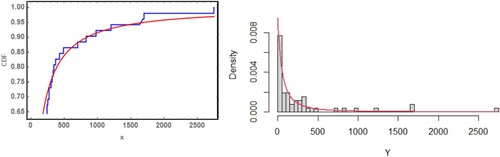
To demonstrate the proposed methodologies, we look at an application to two real data sets in this section. Nelson [35] provided these statistics, which Abd Ellah [36] discussed. The first data set was obtained at a voltage of 34 kV (minutes), and these data represent the time it takes for an insulating fluid between electrodes to break down (minutes). The 19 times to breakdown are recorded as

Table

0.96	4.15	0.19	0.78	8.01	31.75	7.35	6.50	8.27	33.91
32.52	3.16	4.85	2.78	4.67	1.31	12.06	36.71	72.89

Abd Ellah [36] used the Kolmogorov–Smirnov test to evaluate the correctness of the fitted model where the P-value = 0.749683 and statistic value is 0.147477. The estimated pdf and cdf are represented in Figure 8.

Figure 8. Estimated pdf and cdf of the Lo distribution for first data.

Now we will look at what happens if the data are censored. From the uncensored data set, we generate six artificially UHCD sets as follows:

Case 1: $T_1=20,T_2=35,k=10,r=13$ in this situation $D=14,c=T_1=20$.

Case 2: $T_1=20,T_2=35,k=13,r=15$ in this situation $D=15,c=x_{r:n}=31.75$.

Case 3: $T_1=20,T_2=35,k=14,r=18$ in this situation $D=17,c=T_2=35$.

Case 4: $T_1=20,T_2=35,k=15,r=17$ in this situation $D=17,c=x_{r:n}=33.91$.

Case 5: $T_1=20,T_2=35,k=15,r=18$ in this situation $D=17,c=T_2=35$.

Case 6: $T_1=20,T_2=35,k=18,r=19$ in this situation $D=18,c=x_{k,n}=36.71$.

In these cases, we used ML and a Bayesian estimate of Shannon entropy. We used 11,000 MCMC sample and discarded the first 1000 values as “burn-in” under balanced loss functions (BSLE, BLINEX, BGE) when $\omega =0.5$. Since we do not know anything about the priors, we use a non-informative prior to compute the Bayes estimators, thus we choose $a_1=0,b_1=0,a_2=0$ and $b_2=0$, as shown in Table 3.

Table 3. Shannon entropy estimators for first data.

Case	n	r	k	($T_1$, $T_2$)	MLE	BSLE	BLINEX		BGE
							$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$	$(-0.5)$
1		12	10		3.5991	3.03634	2.9408	3.12474	2.93568	3.00388
2		15	13		4.0366	3.56213	3.47079	3.64255	3.48013	3.53606
3	19	18	14	(20,35)	3.5928	3.03346	2.93892	3.12088	2.93377	3.00132
4		17	15		3.7010	3.16048	3.06747	3.24536	3.06623	3.13023
5		18	15		3.7107	3.16606	3.07176	3.25215	3.07069	3.13544
6		19	18		3.5991	3.01452	2.91166	3.10952	2.90488	2.97922

The second data were obtained from a meteorological study by Simpson [37]. The data represent radar-evaluated rainfall from 52 south Florida cumulus clouds. This data set was successfully fitted for the Lo distribution using the Kolmogorov–Smirnov test with a statistic value of 0.0825474 and a P-value $=0.841763$. The estimated pdf and cdf are represented in Figure 9.

Figure 9. Estimated pdf and cdf of Lo distribution for second data.

Now we will look at what happens if the data are censored. From the uncensored data set, we generate six artificially UHCD sets as follows:

Case 1: $T_1=120,T_2=200,k=25,r=27$ in this situation $D=28,c=T_1=120$.

Case 2: $T_1=120,T_2=200,k=25,r=30$ in this situation $D=30,c=x_{r:n}=147.8$.

Case 3: $T_1=120,T_2=200,k=25,r=35$ in this situation $D=34,c=T_2=200$.

Case 4: $T_1=120,T_2=200,k=29,r=31$ in this situation $D=31,c=x_{r:n}=163$.

Case 5: $T_1=120,T_2=200,k=29,r=36$ in this situation $D=36,c=T_2=200$.

Case 6: $T_1=120,T_2=200,k=35,r=37$ in this situation $D=35,c=x_{k,n}=244.3$.

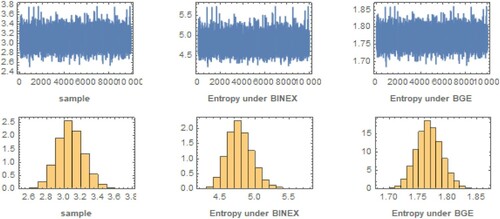
In these cases, we used ML and a Bayesian estimate of Shannon entropy. We used 11,000 MCMC sample and discarded the first 1000 values as “burn-in” under balanced loss functions (BSLE, BLINEX, BGE) when $\omega =0.5$. Since we do not know anything about the priors, we use a non-informative prior to compute the Bayes estimators, thus we choose $a_1=0,b_1=0,a_2=0$ and $b_2=0$, as shown in Table 4. Figures 10 and 11 show the trace plot and histogram of the first 1000 MCMC outputs for posterior distribution of $H\left(x\right)$ for case 1 based on UHCS for first real and second real data respectively.

Figure 10. The trace plot and histogram of posterior samples for case 1 of UHCS for the first real data.

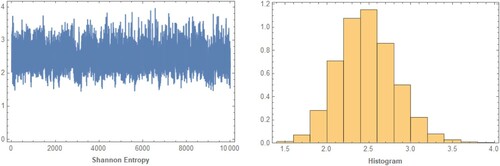
Figure 11. The trace plot and histogram of posterior samples for case 1 of UHCS for the second real data.

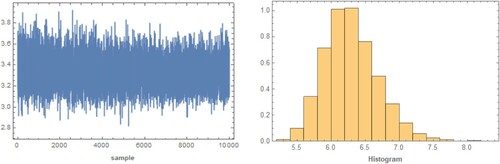
Table 4. Shannon entropy estimators for second data.

Case	n	r	k	($T_1$, $T_2$)	MLE	BSLE	BLINEX		BGE
							$\left(0.5\right)$	$(-0.5)$	$\left(0.5\right)$	$(-0.5)$
1		25	27		6.83432	6.56384	6.5238	6.59975	6.54564	6.55789
2		25	30		6.81259	6.56198	6.51939	6.54533	6.44697	6.46245
3	52	25	35	(120,200)	6.79319	6.3732	6.3137	6.42777	6.34518	6.364
4		29	31		6.92354	6.55417	6.50037	6.60263	6.52961	6.54612
5		29	36		6.86165	6.36148	6.28443	6.43302	6.32491	6.34945
6		35	37		6.94537	6.44828	6.37005	6.52036	6.4117	6.43625

We note from the study of these applications in Tables 3 and 4 the amount of data obtained in Bayesian estimation is larger than at MLE because the uncertainty in the case of Bayesian is less than the uncertainty in MLE.

The BE based on BLINEX and BGE loss functions at $q=0.5$ has a large amount of data where at $q=-0.5$ has a less amount of data because it has a large amount of uncertainty and this is the same result in simulation study.

7. Conclusion and summary

In this paper, the maximum likelihood and Bayesian estimation of Shannon entropy for Lo distribution under UHCS are considered. The Bayesian estimate of Shannon entropy for Lo distribution is obtained based on balanced loss functions (BSEL, BLINEX, BGE). The MCMC method is employed to calculate the Bayesian estimator of Shannon entropy under BSEL, BLINEX, BGE in terms of their mean squared error. Application to real data is provided.

Regarding the simulation results, we conclude that the mean squared error of ML and Bayesian estimates of the Shannon entropy decrease as the sample size increases. The entropy estimates via BLNIEX and BGE loss functions are chosen over the others at $q=-0.5$, allowing for more information. The MLE and BE of Shannon entropy are preferred above the others when $T_1=1.8$, providing more information for fixed values of $r,k,T_2$. The BE has a greater amount of information than MLE since the uncertainty in BE is lower. In future work, one might study the challenge of estimating other measures of uncertainty using the E-Bayesian approach under UHCS. In this study, we used the MCMC method to calculate the Bayesian estimator of Shannon entropy under BSEL, BLINEX, BGE. Other approaches, such as Tierney–Kadane approximation and Lindley approximation will be used along with the MCMC approach under BSEL, BLINEX, BGE or another types of loss functions.

Acknowledgements

The authors would like to express their gratitude to the editor and the anonymous referees for their insightful and constructive remarks, which have significantly improve the paper's substance.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work has no funding from any organization or any person.