Symmetry analysis and conservation laws of the modified Korteweg–de Vries equation with a quartic nonlinear term

Abstract

In this paper, a modified Korteweg–de Vries equation with a quartic nonlinear term in two-electron temperature plasmas is studied. Firstly, the symmetries are constructed using the generalized symmetry method. In addition, the potential equation is studied, it can been found that this equation does not posses potential symmetries. Meanwhile, the symmetry reduction and group-invariant solutions are derived rely on the one-dimensional optimal system of subalgebras. Finally, conservation laws are showed resort by the multipliers method, three polynomial type conserved quantities are presented, also the Hamiltonian form is obtained. In particular, reciprocal Bäcklund transformations for conservation laws are obtained for the first time.

Keywords:

• Modified Korteweg–de vries equation with a quartic nonlinear term
• symmetries
• symmetry reduction
• exact solutions
• conservation laws

PACS Codes:

• 02.20.Sv
• 02.30.Jr
• 04.20.Jb

1. Introduction

In the present paper, we focus on the following equation [1]: (1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) which is derived from the following equations: (2) $\{\begin{array}{l}{\displaystyle \frac{\mathrm{\partial }n}{\mathrm{\partial }t}}+{\displaystyle \frac{\mathrm{\partial }(nu)}{\mathrm{\partial }x}}=0,\\ {\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }t}}+u{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }x}}+{\displaystyle \frac{\mathrm{\partial }\phi }{\mathrm{\partial }x}}=0,\\ {\displaystyle \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}}+n-f\exp {\alpha }_c\phi -(1-f)\exp {\alpha }_h\phi =0.\end{array}$(2) In paper [1], the authors derived this equation, and give solutions and three conservation laws. Motivated by their works, we will study this model from view of symmetry. Because this equation is derived from the actual physical background, it is necessary for us to study it. For this equation, we have not found any author to deal with them in the symmetry method. In fact, this equation belongs to one of the Korteweg de Vries (KdV) family of equations, many authors use various methods to deal with KdV family of equations. We known that the KdV equation is a famous equation in mathematics and physics, which was initially proposed by Korteweg and de Vries [2], this equation was mainly established for surface waves on shallow water. And then, many scientists found that this equation has important applications in many fields [3–6]. In that paper [6], they derived a KdV type equation and obtained some soliton solutions. In our paper, we mainly focus on symmetry and conservation laws for Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ). Many papers have studied high-order KdV equation [7, 8] (and the references therein).

We know that nonlinear science is an important modern science and plays an important role in many fields. Nonlinear evolution equations can be used to describe many complex natural phenomena [9–12]. A natural problem naturally arises: How to solve these nonlinear evolution equation? On the one hand, these equations reflect some natural phenomena and provide a basis for many practical problems; on the other hand, many authors are trying to find some methods to solve the nonlinear evolution equations. We know that until now, there is no unified method to solve nonlinear evolution equations. However, fortunately, after the continuous efforts of many authors, some methods for solving nonlinear evolution equations have been proposed and developed. Some important methods include Lie group methods [13–26], Douboux transformation, Lax pairs, inverse scattering transformation, nonlocal symmetry and so on.

Although this model is simple, it is still necessary to study this equation from another perspective. Firstly, we investigate this equation from view of the symmetry method, and then, symmetry reductions and explicit solutions are given. Meanwhile, conservation laws also derived using the multipliers method, it should be emphasized that we obtain the reciprocal Bäcklund transformations for conservation laws of this equation for the first time.

2. Symmetries analysis for Equation (1)

2.1. Generalized symmetries for Equation (1)

From the generalized symmetry method [14] (pp. 248–250) and [15], for a given nonlinear evolution equation (3) $F(t,x,y,u,u_t,u_x,u_y\dots )=0,$(3) that is to say, for a function σ, it is a symmetry of Equation (3(3) $F(t,x,y,u,u_t,u_x,u_y\dots )=0,$(3) ), when it satisfies (4) $F^{\prime }(u)\sigma =0,$(4) for all solutions u, where (5) $\begin{array}{rl}{F}^{\prime }(u)\sigma & =\frac{\mathrm{\partial }F}{\mathrm{\partial }u}\sigma +\frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_t}{\sigma }_t+\frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_x}{\sigma }_x\\ & +\frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_y}{\sigma }_y+\frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_{tx}}{\sigma }_{tx}+\frac{\mathrm{\partial }F}{\mathrm{\partial }{u}_{xx}}{\sigma }_{xx}+\cdots .\end{array}$(5) Hence, we get (6) ${\sigma }_t+3u^2{u}_x\sigma +3u^3{\sigma }_x+{\sigma }_{xxx}=0.$(6) Now, setting σ, (7) $\sigma =a{u}_x+b{u}_t+eu+g,$(7) where a, b, e, g are functions of t, x to be determined. Replacing (7(7) $\sigma =a{u}_x+b{u}_t+eu+g,$(7) ) into (6(6) ${\sigma }_t+3u^2{u}_x\sigma +3u^3{\sigma }_x+{\sigma }_{xxx}=0.$(6) ) and employing (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), replacing $u_t$ by $-u^3{u}_x-u_{xxx}$, In this way, one should get some partial differential equations, solve them by hand, and obtain (8) $a=3c_{1}x+c_3,b=9c_{1}t+c_2,e=-2c_1,g=0,$(8) here $c_i(i=1,2,3)$ are arbitrary constants. Putting (8(8) $a=3c_{1}x+c_3,b=9c_{1}t+c_2,e=-2c_1,g=0,$(8) ) into (7(7) $\sigma =a{u}_x+b{u}_t+eu+g,$(7) ), we have (9) $\sigma =(3c_{1}x+c_3)u_x+(9c_{1}t+c_2)u_t-2c_{1}u.$(9) It is equivalent to (10) $\sigma =c_1(3x{u}_x+9t{u}_t-2u)+c_2{u}_t+c_3{u}_x.$(10) In this way, one can get the vector field (11) $V=(3c_{1}x+c_3)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(9c_{1}t+c_2)\frac{\mathrm{\partial }}{\mathrm{\partial }t}-2c_{1}u\frac{\mathrm{\partial }}{\mathrm{\partial }u},$(11) or (12) $V_1=\frac{\mathrm{\partial }}{\mathrm{\partial }x},V_2=\frac{\mathrm{\partial }}{\mathrm{\partial }t},V_3=3x\frac{\mathrm{\partial }}{\mathrm{\partial }x}+9t\frac{\mathrm{\partial }}{\mathrm{\partial }t}-2u\frac{\mathrm{\partial }}{\mathrm{\partial }u}.$(12)

2.2. Potential symmetry analysis

For the conservation laws forms, (13) $D_{t}T(x,t,u)+D_{x}X(x,t,u)=0,$(13) where T is the conserved density and X is the conserved flow, we rewrite Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), the following should be obtained (14) $\begin{array}{rl}& v_x=u,\\ & v_t=-(\frac{1}{4}{u}^4+u_{xx}).\end{array}$(14) From the Lie symmetry analysis method [13] (Chapter 2) [16] (Chapter 1), one can obtain the coefficient functions $\tau (x,t,u,v)$, $\xi (x,t,u,v)$,$\eta (x,t,u,v)$ and $\psi (x,t,u,v)$ as (15) $\begin{array}{rl}\tau & =c_{1}t+c_2,\xi =\frac{1}{3}{c}_{1}x+c_3,\\ \eta & =-\frac{2}{9}{c}_{1}u,\psi =\frac{1}{9}{c}_{1}v+c_4,\end{array}$(15) where $c_i(i=1,2,3,4$) are arbitrary constants.

It is shown that this equation does not posses potential symmetries. Consequently, we also derive the potential equation (16) $v_t+\frac{1}{4}{v}_x^4+v_{xxx}=0.$(16) Like the previous steps, we can get the following results for the potential equation: (17) $\tau =9c_{1}t+c_2,\xi =3c_{1}x+c_4,\eta =c_{1}v+c_3.$(17) Therefore, we can get the vector fields for potential equation (16(16) $v_t+\frac{1}{4}{v}_x^4+v_{xxx}=0.$(16) ) (18) $\begin{array}{rl}{V}_1& =\frac{\mathrm{\partial }}{\mathrm{\partial }x},V_2=\frac{\mathrm{\partial }}{\mathrm{\partial }t},V_3=\frac{\mathrm{\partial }}{\mathrm{\partial }v},\\ V_4& =3x\frac{\mathrm{\partial }}{\mathrm{\partial }x}+9t\frac{\mathrm{\partial }}{\mathrm{\partial }t}+v\frac{\mathrm{\partial }}{\mathrm{\partial }v}.\end{array}$(18)

3. Similarity reduction and exact solutions of Equation (1)

3.1. One-dimensional optimal system

Using the adjoint transformations formula [13] (19) $Ad(\exp (ϵV_i))V_j=V_j-ϵ[V_i,V_j]+\frac{1}{2}{ϵ}^2[V_i,[V_i,V_j]]-\cdots$(19) where ϵ is a nonzero constant. $[V_i,V_j]$ is the commutator for the Lie algebra (20) $[V_i,V_j]=V_i{V}_j-V_j{V}_i.$(20) One can derive an optimal system as (21) $V_1,V_2+\lambda V_1,V_3.$(21)

3.2. Symmetry reductions

In this subsection, we employ the optimal system of one-dimensional subalgebras to deal with (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ).

1. $V_1.$

   For this case $V_1$, trivial solution $u(x,t)=C$ is obtained, and C is a constant.

2. $V_2+\lambda V_1$.

Consider the generator $V_2+\lambda V_1$, one can derive the group-invariant solution (22) $u=f(\xi ),$(22) where $\xi =x-\lambda t$. Inserting (22(22) $u=f(\xi ),$(22) ) into (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), following ODE is given (23) $-\lambda f^{\prime }+f^3{f}^{\prime }+f^{(3)}=0.$(23) Integrating, we have (24) $-\lambda f+\frac{1}{4}{f}^4+f^{″}+k=0,$(24) where k is an integration constant. If we assume k = 0, and multiplied by $f^{\prime }$, and integral once, one can get (25) $-\lambda f^2+\frac{1}{10}{f}^5+(f^{\prime }{)}^2=K.$(25)

(3)

$V_3.$

For the vector $V_3$, one can get (26) $u=t^{-\frac{2}{9}}f(\xi ),\xi =x{t}^{-\frac{1}{9}}.$(26) Substitution of (26(26) $u=t^{-\frac{2}{9}}f(\xi ),\xi =x{t}^{-\frac{1}{9}}.$(26) ) into (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), we get (27) $f+\xi f^{\prime }+f^3{f}^{\prime }+f^{(3)}=0.$(27)

4. Explicit solutions of Equation (1) via Equation (27)

Supposing that (27(27) $f+\xi f^{\prime }+f^3{f}^{\prime }+f^{(3)}=0.$(27) ) has the following solution: (28) $f(\xi )=c_0+c_1\xi +c_2{\xi }^2+\cdots =\sum _{n=0}^{\mathrm{\infty }}{c}_n{\xi }^n.$(28) Putting (28(28) $f(\xi )=c_0+c_1\xi +c_2{\xi }^2+\cdots =\sum _{n=0}^{\mathrm{\infty }}{c}_n{\xi }^n.$(28) ) into (27(27) $f+\xi f^{\prime }+f^3{f}^{\prime }+f^{(3)}=0.$(27) ), which leads to (29) $\begin{array}{rl}& 6c_3+\sum _{n=1}^{\mathrm{\infty }}(n+1)(n+2)(n+3)c_{n+3}{\xi }^n\\ & +c_0^3{c}_1+\sum _{n=1}^{\mathrm{\infty }}\sum _{k=0}^n(n+1-k)c_{n+1-k}\\ & \times \sum _{l_1+l_2+l_3=k}{c}_{l_1}{c}_{l_2}{c}_{l_3}{\xi }^n\\ & +\sum _{n=1}^{\mathrm{\infty }}n{c}_n{\xi }^n+(c_0+\sum _{n=1}^{\mathrm{\infty }}{c}_n{\xi }^n)=0.\end{array}$(29) Let n = 0 in (29(29) $\begin{array}{rl}& 6c_3+\sum _{n=1}^{\mathrm{\infty }}(n+1)(n+2)(n+3)c_{n+3}{\xi }^n\\ & +c_0^3{c}_1+\sum _{n=1}^{\mathrm{\infty }}\sum _{k=0}^n(n+1-k)c_{n+1-k}\\ & \times \sum _{l_1+l_2+l_3=k}{c}_{l_1}{c}_{l_2}{c}_{l_3}{\xi }^n\\ & +\sum _{n=1}^{\mathrm{\infty }}n{c}_n{\xi }^n+(c_0+\sum _{n=1}^{\mathrm{\infty }}{c}_n{\xi }^n)=0.\end{array}$(29) ), one has (30) $c_3=\frac{-c_0-c_0^3{c}_1}{6}.$(30) For the more general case of $n\ge 1$, it generates (31) $\begin{array}{rl}{c}_{n+3}& =-\frac{1}{(n+1)(n+2)(n+3)}\\ & \times (\sum _{k=0}^n(n+1-k)c_{n+1-k}\sum _{l_1+l_2+l_3=k}{c}_{l_1}{c}_{l_2}{c}_{l_3}\\ & +n{c}_n+c_n\phantom{\sum _{k=0}^n}).\end{array}$(31) Thus, the power series solution is given by (32) $\begin{array}{rl}f(\xi )& =c_0+c_1\xi +c_2{\xi }^2+c_3{\xi }^3+\sum _{n=1}^{\mathrm{\infty }}{c}_{n+3}{\xi }^{n+3}\\ & =c_0+c_1\xi +c_2{\xi }^2+\frac{-c_0-c_0^3{c}_1}{6}{\xi }^3\\ & \times \sum _{n=1}^{\mathrm{\infty }}-\frac{1}{(n+1)(n+2)(n+3)}\\ & \times (\sum _{k=0}^n(n+1-k)c_{n+1-k}\sum _{l_1+l_2+l_3=k}{c}_{l_1}{c}_{l_2}{c}_{l_3}\\ & +n{c}_n+c_n\phantom{\sum _{k=0}^n}){\xi }^{n+3}.\end{array}$(32) In other words, at last we get a solution of (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ) (33) $\begin{array}{rl}u(x,t)& =[c_0+c_1\left(x{t}^{-\frac{1}{9}}\right)+c_2{\left(x{t}^{-\frac{1}{9}}\right)}^2+c_3{\left(x{t}^{-\frac{1}{9}}\right)}^3\\ & +{\displaystyle \sum _{n=1}^{\mathrm{\infty }}{c}_{n+3}{\left(x{t}^{-\frac{1}{9}}\right)}^{n+3}}]\left(t^{-\frac{2}{9}}\right)\\ & =[c_0+c_1\left(x{t}^{-\frac{1}{9}}\right)+c_2{\left(x{t}^{-\frac{1}{9}}\right)}^2\\ & +\frac{-c_0-c_0^3{c}_1}{6}{\left(x{t}^{-\frac{1}{9}}\right)}^3\\ & -\sum _{n=1}^{\mathrm{\infty }}\frac{1}{(n+1)(n+2)(n+3)}\\ & \times (\sum _{k=0}^n(n+1-k)c_{n+1-k}\sum _{l_1+l_2+l_3=k}{c}_{l_1}{c}_{l_2}{c}_{l_3}\\ & +n{c}_n+c_n\phantom{\sum _{k=0}^n}){\left(x{t}^{-\frac{1}{9}}\right)}^{n+3}]\left(t^{-\frac{2}{9}}\right),\end{array}$(33) here $c_i(i=0,1,2)$ are arbitrary constants. Generally speaking, the series solution is convergent. If we consider n = 3, we get approximate solution as the following form: (34) $\begin{array}{rl}u(x,t)& =[c_0+c_1\left(x{t}^{-\frac{1}{9}}\right)+c_2{\left(x{t}^{-\frac{1}{9}}\right)}^2\\ & +c_3{\left(x{t}^{-\frac{1}{9}}\right)}^3]\left(t^{-\frac{2}{9}}\right)\\ & =[c_0+c_1\left(x{t}^{-\frac{1}{9}}\right)+c_2{\left(x{t}^{-\frac{1}{9}}\right)}^2\\ & +\frac{-c_0-c_0^3{c}_1}{6}{\left(x{t}^{-\frac{1}{9}}\right)}^3]\left(t^{-\frac{2}{9}}\right),\end{array}$(34) here $c_i(i=0,1,2)$ are arbitrary constants.

5. Exact travelling wave solution of Equation (1)

Now we study Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ) has the following hypothetical solution [6, 27, 28]: (35) $u(x,t)=M{\mathrm{sech}}^p(\tau ),$(35) where $\tau =B(x-vt)$, $M,v$ are constants need to be fixed. On the basis of Equation (35(35) $u(x,t)=M{\mathrm{sech}}^p(\tau ),$(35) ), it generates (36) $\begin{array}{rl}& u_t=pvMB{\mathrm{sech}}^p(\tau )\tanh (\tau ),\\ & u_x=-pMB{\mathrm{sech}}^p(\tau )\tanh (\tau ),\\ & u^3{u}_x=-M^{4}pB{\mathrm{sech}}^{4p}(\tau )\tanh (\tau ),\\ & u_{xxx}=-p^{3}M{B}^3{\mathrm{sech}}^p(\tau )\tanh (\tau )\\ & +p(p+1)(p+2)M{B}^3{\mathrm{sech}}^{p+2}(\tau )\tanh (\tau ).\end{array}$(36) Putting Equation (36(36) $\begin{array}{rl}& u_t=pvMB{\mathrm{sech}}^p(\tau )\tanh (\tau ),\\ & u_x=-pMB{\mathrm{sech}}^p(\tau )\tanh (\tau ),\\ & u^3{u}_x=-M^{4}pB{\mathrm{sech}}^{4p}(\tau )\tanh (\tau ),\\ & u_{xxx}=-p^{3}M{B}^3{\mathrm{sech}}^p(\tau )\tanh (\tau )\\ & +p(p+1)(p+2)M{B}^3{\mathrm{sech}}^{p+2}(\tau )\tanh (\tau ).\end{array}$(36) ) into Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), one has (37) $\begin{array}{rl}& pvMB{\mathrm{sech}}^p(\tau )\tanh (\tau )-M^{4}pB{\mathrm{sech}}^{4p}(\tau )\tanh (\tau ),\\ & -p^{3}M{B}^3{\mathrm{sech}}^p(\tau )\tanh (\tau )\\ & +p(p+1)(p+2)M{B}^3{\mathrm{sech}}^{p+2}(\tau )\tanh (\tau ).\end{array}$(37) Considering the exponents $4p$ and p + 2 should be equal, one finds (38) $p=\frac{2}{3},$(38) also, one gets (39) $M^{4}pB=p(p+1)(p+2)M{B}^3,$(39) therefore, one can get (40) $M=\sqrt[3]{\frac{40}{9}{B}^2}.$(40) For the coefficient of term ${\mathrm{sech}}^p(\tau )\tanh (\tau )$, one can yield (41) $v=\frac{4}{9}{B}^2.$(41) Finally, we get the soliton solution as (42) $u(x,t)=\sqrt[3]{\frac{40}{9}{B}^2}{\mathrm{sech}}^{\frac{2}{3}}\left(B(x-\frac{4}{9}{B}^{2}t)\right).$(42) In fact, this solution is equivalent to the solution in reference [1], which we derive from a different perspective.

Also considering Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ) has the following hypothetical solution: (43) $u(x,t)=M{\mathrm{csch}}^p(\tau ),$(43) where $\tau =B(x-vt)$, $M,v$ are constants need to be calculated. On the basis of Equation (43(43) $u(x,t)=M{\mathrm{csch}}^p(\tau ),$(43) ), it generates (44) $\begin{array}{rl}& u_t=pvMB{\mathrm{csch}}^p(\tau )\coth (\tau ),\\ & u_x=-pMB{\mathrm{csch}}^p(\tau )\coth (\tau ),\\ & u^3{u}_x=-M^{4}pB{\mathrm{csch}}^{4p}(\tau )\coth (\tau ),\\ & u_{xxx}=-p^{3}M{B}^3{\mathrm{csch}}^p(\tau )\coth (\tau )\\ & -p(p+1)(p+2)M{B}^3{\mathrm{csch}}^{p+2}(\tau )\coth (\tau ).\end{array}$(44) Putting Equation (44(44) $\begin{array}{rl}& u_t=pvMB{\mathrm{csch}}^p(\tau )\coth (\tau ),\\ & u_x=-pMB{\mathrm{csch}}^p(\tau )\coth (\tau ),\\ & u^3{u}_x=-M^{4}pB{\mathrm{csch}}^{4p}(\tau )\coth (\tau ),\\ & u_{xxx}=-p^{3}M{B}^3{\mathrm{csch}}^p(\tau )\coth (\tau )\\ & -p(p+1)(p+2)M{B}^3{\mathrm{csch}}^{p+2}(\tau )\coth (\tau ).\end{array}$(44) ) into Equation (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ), one gets (45) $\begin{array}{rl}& pvMB{\mathrm{csch}}^p(\tau )\coth (\tau )-M^{4}pB{\mathrm{csch}}^{4p}(\tau )\coth (\tau ),\\ & -p^{3}M{B}^3{\mathrm{csch}}^p(\tau )\coth (\tau )\\ & -p(p+1)(p+2)M{B}^3{\mathrm{csch}}^{p+2}(\tau )\coth (\tau ).\end{array}$(45) Using the same method, one can obtain (46) $\begin{array}{rl}p& =\frac{2}{3},\\ M& =\sqrt[3]{-\frac{40}{9}{B}^2},\\ v& =\frac{4}{9}{B}^2.\end{array}$(46) At last, a soliton solution is given by (47) $u(x,t)=\sqrt[3]{-\frac{40}{9}{B}^2}{\mathrm{csch}}^{\frac{2}{3}}\left(B(x-\frac{4}{9}{B}^{2}t)\right).$(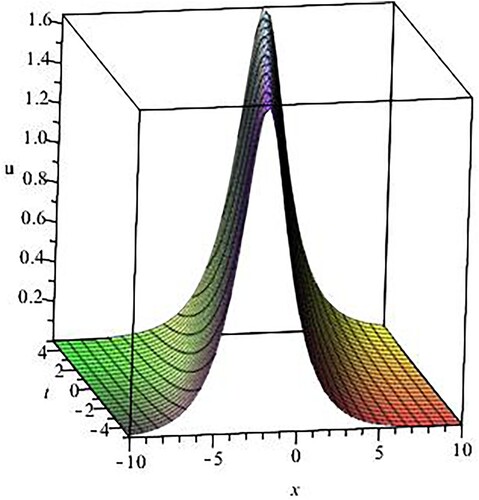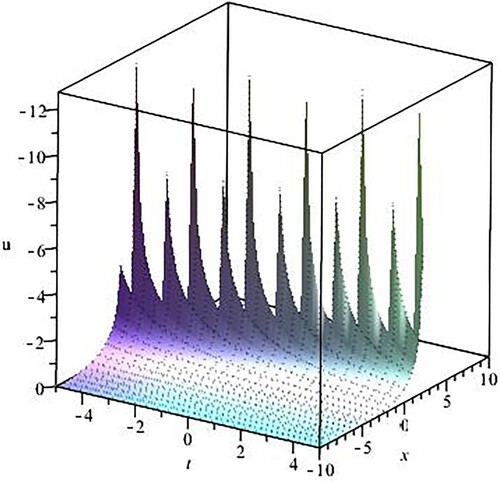47) Some special cases of the solution (B = 1) are shown in Figures 1 and 2.

Figure 1. $u(x,t)=\sqrt[3]{\frac{40}{9}}{\mathrm{sech}}^{\frac{2}{3}}((x-\frac{4}{9}t))$

Figure 2. $u(x,t)=\sqrt[3]{-\frac{40}{9}}{\mathrm{csch}}^{\frac{2}{3}}((x-\frac{4}{9}t))$

6. Conservation laws

In this section, by employing the multipliers method [16], one can get the multipliers, (48) $\begin{array}{rl}& \mathrm{\Lambda }1(t,x,u,{\mathit{u}}_{\mathit{x}}\mathit{,}{\mathit{u}}_{\mathit{x}\mathit{x}}\mathit{,}{\mathit{u}}_{\mathit{x}\mathit{x}\mathit{x}}\mathit{,}{\mathit{u}}_{\mathit{x}\mathit{x}\mathit{x}\mathit{x}\mathit{x}}\mathit{,}{\mathit{u}}_{\mathit{x}\mathit{x}\mathit{x}\mathit{x}\mathit{x}\mathit{x}\mathit{x}})\\ & =\frac{1}{4}{C}_1(u^4+4u_{xx})+C_{2}u+C_3.\end{array}$(48) For the case multiplier $\frac{1}{4}(u^4+4u_{xx})$, we have, (49) $\{\begin{array}{l}{T}^t=\frac{1}{20}{u}^5+\frac{1}{2}u{u}_{xx},T^x=\frac{1}{32}{u}^8+\frac{1}{4}{u}^4{u}_{xx}+\frac{1}{2}{u}_{xx}^2-\frac{1}{2}u{u}_{tx}+\frac{1}{2}{u}_x{u}_t.\end{array}$(49) One can assume that this conservation law means conservation of energy.

For the multiplier u, we get (50) $\{\begin{array}{l}{T}^t=\frac{1}{2}{u}^2,T^x=\frac{1}{5}{u}^5+u{u}_{xx}-\frac{1}{2}{u}_x^2.\end{array}$(50) This conservation laws can been seen as conservation of momentum.

Consider the multiplier 1, one has (51) $\{\begin{array}{l}{T}^t=u,T^x=\frac{1}{4}{u}^4+u_{xx}.\end{array}$(51) This conservation laws presents the conservation of mass.

In this way, one can get the three polynomial type conserved quantities (52) $\{\begin{array}{l}{I}_1={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{H}_1\mathrm{d}x={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}u\mathrm{d}x,I_2={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{H}_2\mathrm{d}x={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{2}{u}^2\mathrm{d}x,I_3={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{H}_3\mathrm{d}x={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(\frac{1}{20}{u}^5+\frac{1}{2}u{u}_{xx})\mathrm{d}x.}}}}}}\end{array}$(52) Therefore, we can rewrite (1(1) $u_t+u^3{u}_x+u_{xxx}=0,$(1) ) in the following Hamiltonian form: (53) $u_t=-\frac{\mathrm{\partial }}{{\mathrm{\partial }}_x}\frac{\delta H_3}{{\delta }_u}.$(53)

6.1. Conservation laws of potential equation (16)

For the potential equation, one obtains the fourth-order multipliers, (54) $\begin{array}{rl}& \mathrm{\Lambda }1(t,x,v,{\mathit{v}}_{\mathit{x}}\mathit{,}{\mathit{v}}_{\mathit{x}\mathit{x}}\mathit{,}{\mathit{v}}_{\mathit{x}\mathit{x}\mathit{x}}\mathit{,}{\mathit{v}}_{\mathit{x}\mathit{x}\mathit{x}\mathit{x}})\\ & =C_1(v_{xxxx}+v_{xx}{v}_x^3)+C_2{v}_{xx}.\end{array}$(54) For the multiplier $v_{xxxx}+v_{xx}{v}_x^3$, one can get (55) $\{\begin{array}{l}{T}^t=\frac{1}{5}v{v}_{xx}{v}_x^3+\frac{1}{2}v{v}_{xxxx},T^x=\frac{1}{32}{v}_x^8-\frac{1}{5}v{v}_{tx}{v}_x^3+\frac{1}{5}{v}_x^4{v}_t-\frac{1}{2}v{v}_{txxx}+\frac{1}{2}{v}_x{v}_{txx}\\ -\frac{1}{2}{v}_{xx}{v}_{tx}+\frac{1}{2}{v}_t{v}_{xxx}+\frac{1}{2}{v}_{xxx}^2.\end{array}$(55) Consider the multiplier $v_{xx}$, one should derive (56) $\{\begin{array}{l}{T}^t=\frac{1}{2}v{v}_{xx},T^x=\frac{1}{20}{v}_x^5+\frac{1}{2}{v}_{xx}^2-\frac{1}{2}v{v}_{tx}+\frac{1}{2}{v}_x{v}_t.\end{array}$(56)

7. Reciprocal Bäcklund transformations of conservation laws

In paper [29], the authors derived the reciprocal Bäcklund transformations of conservation laws. On the basis of that paper, one has

Theorem 7.1

[29]

The conservation law (57) $\frac{\mathrm{\partial }}{{\mathrm{\partial }}_t}\left\{T(\mathrm{\partial }/{\mathrm{\partial }}_x;\mathrm{\partial }/{\mathrm{\partial }}_t;u)\right\}+\frac{\mathrm{\partial }}{{\mathrm{\partial }}_x}\left\{F(\mathrm{\partial }/{\mathrm{\partial }}_x;\mathrm{\partial }/{\mathrm{\partial }}_t;u)\right\}=0$(57) is connected reciprocally to associated conservation law (58) $\frac{\mathrm{\partial }}{{\mathrm{\partial }}_{t^{\prime }}}\left\{T^{\prime }(\mathrm{\partial }/{\mathrm{\partial }}_{x^{\prime }};\mathrm{\partial }/{\mathrm{\partial }}_{t^{\prime }};u)\right\}+\frac{\mathrm{\partial }}{{\mathrm{\partial }}_{x^{\prime }}}\left\{F^{\prime }(\mathrm{\partial }/{\mathrm{\partial }}_{x^{\prime }};\mathrm{\partial }/{\mathrm{\partial }}_{t^{\prime }};u)\right\}=0,$(58) using the reciprocal transformation (59) $\mathrm{d}{x}^{\prime }=T\mathrm{d}x-F\mathrm{d}t,t^{\prime }=t,$(59) where (60) $T^{\prime }T=1,F^{\prime }T=-F.$(60)

Therefore, as to multiplier $\frac{1}{4}{u}^4+u_{xx}$, we get reciprocal Bäcklund transformations of conservation laws for (49(49) $\{\begin{array}{l}{T}^t=\frac{1}{20}{u}^5+\frac{1}{2}u{u}_{xx},T^x=\frac{1}{32}{u}^8+\frac{1}{4}{u}^4{u}_{xx}+\frac{1}{2}{u}_{xx}^2-\frac{1}{2}u{u}_{tx}+\frac{1}{2}{u}_x{u}_t.\end{array}$(49) ), (61) $\{\begin{array}{l}(T^t{)}^{\prime }={\displaystyle \frac{1}{T}}={\displaystyle \frac{1}{\frac{1}{20}{u}^5+\frac{1}{2}u{u}_{xx}}},(T^x{)}^{\prime }=-{\displaystyle \frac{F}{T}}=-{\displaystyle \frac{\begin{array}{c}\frac{1}{32}{u}^8+\frac{1}{4}{u}^4{u}_{xx}\\ +\frac{1}{2}{u}_{xx}^2-\frac{1}{2}u{u}_{tx}+\frac{1}{2}{u}_x{u}_t\end{array}}{\frac{1}{20}{u}^5+\frac{1}{2}u{u}_{xx}}}.\end{array}$(61) If the multiplier is u, we get (62) $\{\begin{array}{l}(T^t{)}^{\prime }={\displaystyle \frac{1}{T}}={\displaystyle \frac{2}{u^2}},\\ (T^x{)}^{\prime }=-{\displaystyle \frac{F}{T}}=-{\displaystyle \frac{\frac{1}{5}{u}^5+u{u}_{xx}-\frac{1}{2}{u}_x^2}{\frac{1}{2}{u}^2}}.\end{array}$(62) If the case multiplier is 1, we have (63) $\{\begin{array}{l}(T^t{)}^{\prime }={\displaystyle \frac{1}{T}}={\displaystyle \frac{1}{u}},(T^x{)}^{\prime }=-{\displaystyle \frac{F}{T}}=-{\displaystyle \frac{\frac{1}{4}{u}^4+u_{xx}}{u}},\end{array}$(63) or equivalently (64) $(T^t{)}_{t^{\prime }}^{\prime }+(T^x{)}_{x^{\prime }}^{\prime }=0.$(64) Using the same steps, we can derive reciprocal Bäcklund transformations for conservation laws of the potential equation.

For the multiplier $v_{xxxx}+v_{xx}{v}_x^3$, one can get reciprocal Bäcklund transformations (65) $\{\begin{array}{l}(T^t{)}^{\prime }={\displaystyle \frac{1}{T}}={\displaystyle \frac{1}{\frac{1}{5}v{v}_{xx}{v}_x^3+\frac{1}{2}v{v}_{xxxx}}},(T^x{)}^{\prime }=-{\displaystyle \frac{F}{T}}=-{\displaystyle \frac{\begin{array}{c}\frac{1}{32}{v}_x^8-\frac{1}{5}v{v}_{tx}{v}_x^3+\frac{1}{5}{v}_x^4{v}_t\\ -\frac{1}{2}v{v}_{txxx}+\frac{1}{2}{v}_x{v}_{txx}-\frac{1}{2}{v}_{xx}{v}_{tx}\\ +\frac{1}{2}{v}_t{v}_{xxx}+\frac{1}{2}{v}_{xxx}^2\end{array}}{\frac{1}{5}v{v}_{xx}{v}_x^3+\frac{1}{2}v{v}_{xxxx}}}.\end{array}$(65) When the multiplier is $u_{xx}$, one can arrive at (66) $\{\begin{array}{l}(T^t{)}^{\prime }={\displaystyle \frac{1}{T}}={\displaystyle \frac{1}{\frac{1}{2}v{v}_{xx}}},(T^x{)}^{\prime }=-{\displaystyle \frac{F}{T}}={\displaystyle \frac{\frac{1}{20}{v}_x^5+\frac{1}{2}{v}_{xx}^2-\frac{1}{2}v{v}_{tx}+\frac{1}{2}{v}_x{v}_t}{\frac{1}{2}v{v}_{xx}}}.\end{array}$(66)

8. Conclusions

In the present paper, we investigated the symmetries, symmetry reductions and conservation laws of a modified Korteweg–de Vries equation with a quartic nonlinear term. First, we employed a generalized symmetry analysis method to derive symmetries for this equation, and get its infinitesimal generators. Also, some explicit solutions and conservation laws are presented. Meanwhile, reciprocal Bäcklund transformations for conservation laws are showed for the first time.

In this paper, we studied this equation based on the symmetry method, and we presented the potential symmetry of this equation, and we found that this equation, for our hypothesis, does not have potential symmetry. Using Lie algebra, we derived an optimal system for this equation, and using the optimal system, we have simplified this equation. Then the series method is used to obtain the explicit solution of the original equation. Then the reciprocal Bäcklund transformations for conservation laws of the equation are obtained. The conservation law of the potential equation and the reciprocal Bäcklund transformations for conservation laws of the potential equation are also studied. We found that the symmetry group method is a very effective method to deal with differential equations.

These results are of great help to explain the complicated nonlinear physical phenomena. In this paper, we studied a simple cubic nonlinear equation model, where there are still many issues to be considered, such as discrete case, fractional order case, variable coefficient case and so on. These topics will be reported in future works.

Disclosure statement

No potential conflict of interest was reported by the author(s).