Overtaking interactions of nonlinear ultra-low frequency multi-shock structures in non-relativistic and ultra-relativistic degenerate plasmas

Abstract

A Burgers’ equation (BE) is obtained to examine the overtaking interactions of nonlinear ultra-low frequency (ULF) shock waves, in two cases, in non-relativistic and ultra-relativistic degenerate plasmas consisting of inertial mobile heavy-ion fluid and inertialess light ions and electrons. The Cole–Hopf transformation and the exponential function have been employed to obtain nonlinear ULF multi-shock structures. From the careful analysis, it is found that the overtaking collisions of ULF multi-shock waves and their electric fields are significantly modified with the influence of heavy-ion kinematic viscosity. It is shown that the amplitude and the steepness of ULF multi-shock waves increase with the decrease in the light-to-heavy ion density ratio. Numerical simulations of overtaking collisions are used to shed light on the dynamics of ULF multi-shock waves in astrophysical plasmas such as white dwarf stars.

KEYWORDS:

• Nonlinear ultra-low frequency multi-shock waves
• overtaking collisions
• ultra-relativistic degenerate plasmas

1. Introduction

Over the past decades, the nonlinear propagation of waves in multiple media has been gaining interest due to its potential applications [1–10], in compact astrophysical objects [11–13], such as white dwarf stars, and in laboratories, such as solid explosives [14], ultra-small electronic devices [15], and in high-intensity laser-produced plasmas [16]. In fact, nonlinear waves such as shock wave structures have a powerful influence on many astrophysical states. For instance, the stars’ luminosity is amplified as the total energy emitted from the galaxy is increased due to the explosions that can be detected in the stars. Of course, various ways are applied to interpret the light emitted from the explosion [17]. Accordingly, the generation of nonlinear shock waves is one of the most probable mechanisms because they propagate outward. Besides the strong field generation in the bowshock region, the nonlinear dynamics are recorded in the solar wind [18,19]. In addition, the formation of shock waves is useful for various theoretical simulations. For example, it is known that the nonlinear propagation of shock waves in degenerate relativistic plasmas plays a critical role in understanding the formation and collapse of compact objects. Van Riper [17] considered that the reflection shock begins as the rebounding inner core intercepts the infalling mass above it and imparts the velocity of the core, V_rebound, to that mass. In the first rebound, the kinetic energy of the inner core is comparable to the gravitational potential energy, ΔPE, released in the collapse, (V_rebound)² = 2ΔPE/M_core. Due to this velocity, the intercepted mass has outward-directed kinetic energy of (ΔPE/M_core)4πR_core2ρ ΔR, where ΔR is the change in radius of the homologously bouncing inner core, between maximum compression and subsequent zenith, ρ is the density just outside the inner core, and M_core ≈ M_{chandrasekhar} ≈ 1.4 M_ʘ, where M_ʘ is the solar mass. Of course, for larger bounces, the reflection shock gains more energy, and then more energy reaches finally the surface of the white dwarf star. Based on all these observations and facts, let us focus on studying the nonlinear dynamics of shock structures in astrophysical compact objects, such as white dwarfs. Furthermore, the experimental observations and theoretical simulations of white dwarf stars indicate that interiors of white dwarfs composed on a dense solid surrounded by degenerate electrons, light and heavy nuclei [20,21]. Chandrasekhar [22] first considered that the cores of white dwarf stars contain pure helium nuclei. Moreover, Koester [20] noted that the cores of white dwarf stars consist of carbon/oxygen nuclei, rather than helium nuclei, nuclei of heavy elements such as rubidium, as well as electrons that are relativistic degenerate only within the inner cores of the white dwarfs, but they are non-relativistic degenerate in their outer mantle of the white dwarfs [23]. Recently, Garcia et al. [24] referred that the main constituents of white dwarfs are nuclei of heavy and light elements as well as degenerate electrons. The degenerate pressure of electrons and light nuclei (i.e. degenerate particles) can be given by ${\text{P}}_{\text{j}}={\mathrm{\Gamma }}_{\text{j}}{\text{n}}^{{\gamma }_{\text{j}}}$ with ${\gamma }_{\text{j}}=4/3$; ${\mathrm{\Gamma }}_{\text{j}}=3\hslash \text{c}(\pi /3{)}^{2/3}/4$ for the ultra-relativistic limit [25–28] and ${\gamma }_{\text{j}}=5/3$; ${\mathrm{\Gamma }}_{\text{j}}={\hslash }^2(\pi {)}^{2/3}/5{\text{m}}_{\text{j}}$ for the non-relativistic limit [25–28], where ${\text{m}}_{\text{j}}$ is the mass of the degenerate particles $\hslash \left(=\text{h}/2\pi \right)$ is the reduced Planck’s constant, c denotes the speed of light and the subscript j refers to e and $\ell$ for the electron and for the light ion, respectively.

The nonlinear excitations of shock waves are newly valuable for several theoretical speculations. In particular, many authors have recently carried out a number of theoretical works on the nonlinear propagation of shock waves in degenerate relativistic plasmas [29–34]. For example, Mamun and Zobaer [30] examined the characteristics of shock waves and double layers in a degenerate dense plasma, which contains inertial viscous ion fluid, non-relativistic and ultra-relativistic degenerate electron fluid as well as the negatively charged stationary heavy element. Islam et al. [33] investigated nonlinear ultra-low frequency (ULF) shock waves in a degenerate relativistic three-component plasma model through Burgers’ nonlinear equation. Hafez et al. [34] studied the ion-acoustic shock waves in weakly and highly relativistic plasmas consisting of relativistic ion fluids, nonextensive electrons and positrons by deriving Burgers’ equation (BE). Recently, El-Shamy et al. [35] examined the effects of the chemical potentials, ultra-relativistic and degenerate of electrons and positrons on the physical nature of three-dimensional isothermal ion-acoustic shock waves. It is interesting to state here that all the earlier studies [29–35] are only limited to propagating shock waves in degenerate relativistic plasmas. However, in order for these investigations to be more true, the shock waves collisions must be examined. So, the study of overtaking collisions is of particular importance in astrophysical compact objects. Despite a few authors have studied overtaking collisions of multi-shock wave structures [36,37]. Hafez et al. [37] examined for instance the impacts of the population of nonthermal electrons, α, and strength of non-extensive electrons, q, on overtaking collisions of ion-acoustic multi-shocks in an unmagnetized plasma with positive and negative ions, and (α, q)-distributed electrons. They [37] stated that the amplitudes and thicknesses of ion-acoustic shock waves increase and decrease, respectively, with the increase in q and α. While the overtaking interactions of ULF multi-shock structures in two cases, in degenerate relativistic and non-relativistic plasmas, have not yet been discussed. So the motivation for the present work is to discuss the nonlinear dynamics of ULF multi-shock waves due to the overtaking collisions in white dwarf stars in the above two cases.

There are a lot of observations of pulsating white dwarf stars that are in the range from 2 to 35 min and can be referred to as nonradial gravity oscillation modes. These observations and theories of pulsating white dwarfs are applied to examine the rotation period, mass and the equation of state of pulsating white dwarf stars [38,39]. Besides the gravity waves, the theoretical simulations also predict the propagation of acoustic modes where the degenerate electrons provide the restoring force and nondegenerate ions provide the inertia. Actually, the acoustic modes take a few seconds to propagate through the stars, which is shorter than gravity mode oscillations. For this reason, despite the excitation of acoustic modes, but we have not yet been able to observe them. Of course, the lack of monitoring does not necessarily indicate the loss of acoustic modes but may be related to the activity below the observational threshold [40]. In advance, it should be noted here that acoustic modes were predicted and the possibility of small amplitude acoustic waves propagating is also suggested in the situation of extreme events such as supernova explosions and pulsating white dwarf stars [40,41]. Therefore, our aim here is to enhance a simulation of nonlinear shock waves in a dense plasma with non-relativistic and ultra-relativistic degenerate electrons such as pulsating white dwarf stars.

In the present study, the governing equations are provided and then the Burgers’ equation (BE) is obtained, as in Section 2. Using the Cole–Hopf transformation and the exponential function, overtaking collisions of ULF multi-shock waves are discussed in Section 3. Numerical simulation and discussion are presented in Section 4.

2. Governing equations

We consider the nonlinear propagation of ULF shock waves in a three-component degenerate plasma consisting of nondegenerate inertial heavy-ion fluid, inertialess degenerate light ion and electron fluids. The governing equations of the present plasma model are given by [29,30,33]: (1) $\begin{array}{rl}& \frac{\mathrm{\partial }{\text{n}}_{\text{h}}}{\mathrm{\partial }\text{t}}+\frac{\mathrm{\partial }\left({\text{n}}_{\text{h}}{\text{u}}_{\text{h}}\right)}{\mathrm{\partial }\text{x}}=0,\end{array}$(1) (2) $\begin{array}{rl}& \left(\frac{\mathrm{\partial }{\text{u}}_{\text{h}}}{\mathrm{\partial }\text{t}}+{\text{u}}_{\text{h}}\frac{\mathrm{\partial }{\text{u}}_{\text{h}}}{\mathrm{\partial }x}\right)=-\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }x}+\eta \frac{{\mathrm{\partial }}^2{\text{u}}_{\text{h}}}{\mathrm{\partial }{x}^2},\end{array}$(2) (3) $\begin{array}{rl}& {\mu }_{\text{j}}\frac{\mathrm{\partial }{\text{n}}_{\text{j}}^{{\gamma }_{\text{j}}}}{\mathrm{\partial }\text{x}}+\delta {\text{n}}_{\text{j}}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\text{x}}=0,\end{array}$(3) (4) $\begin{array}{rl}& \frac{{\mathrm{\partial }}^2\varphi }{\mathrm{\partial }{\text{x}}^2}=\left(\text{β}{\text{n}}_{\text{e}}-\alpha {\text{n}}_{\ell }-{\text{n}}_{\text{h}}\right),\end{array}$(4) where $\delta$ refers to 1 (−1) for the light ions (the electrons), ${\mu }_j={\mathrm{\Gamma }}_j{n}_j^{\left(0\right){\gamma }_j-1}/Z_j{m}_e{c}^2$, $\text{β}=n_e^{\left(0\right)}/Z_h{n}_h^{\left(0\right)}$ and $\alpha =Z_{\ell }{n}_{\ell }^{\left(0\right)}/Z_h{n}_h^{\left(0\right)}$. Here, $Z_h$ and $Z_{\ell }$ are the charge states of heavy and light ions, respectively,$Z_e=1$, $n_j^{\left(0\right)}$ and ${\gamma }_j$ are, respectively, the unperturbed number density and the relativistic parameter of the plasma species j, $n_h^{\left(0\right)}$ is the unperturbed number density of the heavy ions, where the subscript h refers to the heavy ions. The quasi-neutrality condition at equilibrium reads: $\text{β}=1+\alpha$. Here the densities $n_h,n_{\ell }\text{and}{n}_e$ are the number density of the heavy ions, the number density of light ions and the number density of electrons, respectively. In the above equations, $u_h$ is the heavy ion fluid velocity and $\varphi$ is the electrostatic potential. We consider the following normalization: $n_h\to n_h/n_h^{\left(0\right)},n_{\ell }\to n_{\ell }/n_{\ell }^{\left(0\right)},n_e\to n_e/n_e^{\left(0\right)},u_h\to u_h/C_{IAS},\varphi \to e\varphi /m_e{c}^2,$ $x\to x/{\lambda }_{DL},\text{and}t\to t/{\omega }_{ph}^{-1}$, $n_{\ell }^{\left(0\right)}$ is the unperturbed number density of light ions, $n_e^{\left(0\right)}$ is the unperturbed number density of electrons, $C_{IAS}\left(=\sqrt{Z_h{m}_e{c}^2/m_h}\right)$, ${\lambda }_{DL}\left(=\sqrt{m_e{c}^2/4\pi Z_h{e}^2{n}_h^{\left(0\right)}}\right)$ and ${\omega }_{ph}^{-1}\left(=\sqrt{m_h/4\pi e^2{Z}_h^2{n}_h^{\left(0\right)}}\right)$ are the heavy ion acoustic speed, the Debye length and the inverse of the heavy ion plasma frequency, orderly. The heavy-ion kinematic viscosity is given by $\eta \left(={\eta }_h{C}_{IAS}/m_h{n}_h^{\left(0\right)}{\lambda }_{DL}^2\right)$, where ${\eta }_h$ is the heavy-ion dynamic viscosity. Interestingly, it should be mentioned here that we can utilize the expression ULF shock waves instead of ion-acoustic shock waves because the inertia is supported by the heavier ions, while the restoring force is given by the degenerate pressure of the degenerate particles (i.e. the lighter ions and electrons). Therefore, ULF shock waves can propagate rather than ion-acoustic shock waves in normal plasmas (i.e. electron-ion plasmas).

In general, most theoretical investigations about the nonlinear propagation of waves in plasma models depend on the reductive perturbation method [42] to obtain the nonlinear evolution equation. The main principles of reductive perturbation method [42] are based on multiple scale expansion. Therefore, we need to know the appropriate coordinate frame that is used to properly describe the plasma model equations. Now, let us expand all the dependent variables in terms of a small $\left(\ll 1\right)$ and real parameter $ϵ$. Obviously, the dispersion or dissipation characteristics of propagating electrostatic mode ($\omega$, k) is derived by linearizing the governing equations, such as (1)–(4), whose all of the perturbed physical quantities are directly proportional to $e^{i\mathrm{\Theta }}$, where $\mathrm{\Theta }\left(x,t\right)\left(=k_{i}x-\omega \left(k_i\right)t\right)$, $\omega$ is the wave frequency and $k_i$ is the wave number and the function $\omega \left(k_i\right)$ achieved the dispersion or dissipation relations in terms of the wave number. In addition, we can assume $k_i={ϵ}^r{K}_i$, where $K_i$ is the new wave number and r is the real number. Substituting the last expression for $k_i$ in the above formulated mathematical expression for $\mathrm{\Theta }\left(x,t\right),$ we have (5) $\mathrm{\Theta }\left(x,t\right)={ϵ}^r{K}_{i}x-\omega \left({ϵ}^r{K}_i\right)t.$(5) It should be mentioned here that purely dissipative media cannot have a mixture of both odd and even terms in $k_i$ in the Taylor expansion of $\omega \left(k_i\right)$. Therefore, in the case of purely dissipative media, the even terms in $k_i$ for the Taylor expansion of $\omega \left(k_i\right)$ can be expressed by (6) $\omega \left(k_i\right)=\stackrel{\mathrm{\prime }}{\omega }\left(0\right){ϵ}^r{K}_i+\stackrel{\mathrm{\prime }}{\stackrel{\mathrm{\prime }}{\omega }}\left(0\right){ϵ}^{2r}{K}_i^2+\cdots$(6) As a result, $\mathrm{\Theta }\left(x,t\right)$ can be given by (7) $\mathrm{\Theta }\left(x,t\right)={ϵ}^r{K}_i\left(x-\stackrel{\mathrm{\prime }}{\omega }\left(0\right)t\right)-{ϵ}^{2r}{K}_i^2\stackrel{\mathrm{\prime }}{\stackrel{\mathrm{\prime }}{\omega }}\left(0\right)t,$(7) where $\stackrel{\mathrm{\prime }}{\omega }\left(0\right)$ and $\stackrel{\mathrm{\prime }}{\stackrel{\mathrm{\prime }}{\omega }}\left(0\right)$ are constants. Thus the space, x, and time, t, can be written as (8) $\zeta ={ϵ}^r\left(x-\lambda t\right)\text{and}\tau ={ϵ}^{2r}t.$(8) In the model at hand, the reductive perturbation method [38] is utilized to construct a nonlinear evolution equation (i.e. Burgers’ equation (BE)) for examining the excitation of ULF shock waves, which leads to the scaling of the independent variables through the stretched coordinates by taking r = 1 into account as (9) $\zeta =ϵ\left(x-\lambda t\right),\text{and}\tau ={ϵ}^{2}t,$(9) where $\lambda$ is the unknown propagation speed of shock waves normalized by the ion acoustic speed. In addition, we have expanded the dependent quantities as (10a) $\psi ={\psi }^{\left(0\right)}+\sum _{n=1}^{\mathrm{\infty }}{ϵ}^n{\psi }^{\left(n\right)},$(10a) where (10b) $\psi =\left[n_h,u_h,\varphi \right]\text{and}{\psi }^{\left(0\right)}=\left[1,0,0\right].$(10b) Putting stretching and perturbation expansions given in Equations (9) and (10) in the governing equations (i.e. Equations (1)–(4)) and equating the coefficients of the different power of $ϵ$, we get a set of equations. (11a) $\begin{array}{rl}{n}_h^{\left(1\right)}& =\frac{1}{{\lambda }^2}{\varphi }^{\left(1\right)},\end{array}$(11a) (11b) $\begin{array}{rl}{u}_h^{\left(1\right)}& =\frac{1}{\lambda }{\varphi }^{\left(1\right)},\end{array}$(11b) (11c) $\begin{array}{rl}{n}_{\ell }^{\left(1\right)}& =-\frac{1}{{\mu }_{\ell }{\gamma }_{\ell }}{\varphi }^{\left(1\right)},\end{array}$(11c) (11d) $\begin{array}{rl}{n}_e^{\left(1\right)}& =\frac{1}{{\mu }_e{\gamma }_e}{\varphi }^{\left(1\right)},\end{array}$(11d) (12) $\begin{array}{rl}\lambda & =\sqrt{\frac{1}{\frac{\text{β}}{{\mu }_e{\gamma }_e}+\frac{\alpha }{{\mu }_{\ell }{\gamma }_{\ell }}}}.\end{array}$(12)

Again, following the same method, the next-higher order comparison in $ϵ$ yields the BE [29,33] (13) $\frac{\mathrm{\partial }{\varphi }^{\left(1\right)}}{\mathrm{\partial }\tau }+A{\varphi }^{\left(1\right)}\frac{\mathrm{\partial }{\varphi }^{\left(1\right)}}{\mathrm{\partial }\zeta }=B\frac{{\mathrm{\partial }}^2{\varphi }^{\left(1\right)}}{\mathrm{\partial }{\zeta }^2},$(13) where A and B are, respectively, the coefficient of nonlinear term and the dissipative coefficient, A and B are given by (14a) $\begin{array}{rl}A& =\frac{3}{2\lambda }-\frac{{\lambda }^3}{2}\left(\text{β}\frac{\left(2-{\gamma }_e\right)}{{\left({\mu }_e{\gamma }_e\right)}^2}-\alpha \frac{\left(2-{\gamma }_{\ell }\right)}{{\left({\mu }_{\ell }{\gamma }_{\ell }\right)}^2}\right),\end{array}$(14a) (14b) $\begin{array}{rl}B& =\frac{\eta }{2}.\end{array}$(14b) For the ULF shock wave solution of Equation (13), we make the following change of variable: $\xi =\zeta -v_0\tau$, where $v_0$ is the speed of the shock wave in the moving reference frame. Therefore, the effective velocity of the shock wave is given by $\lambda +v_0,$ where $\lambda$ is the velocity of the moving frame. Using the boundary conditions: ${\varphi }^{\left(1\right)}\to 0,d{\varphi }^{\left(1\right)}/d\xi \to 0,d^2{\varphi }^{\left(1\right)}/d{\xi }^2\to 0\text{at}\xi \to \pm \mathrm{\infty }.$ Accordingly, we can write the ULF shock wave solution of Equation (13) as [29,33]. (15) ${\varphi }^{\left(1\right)}={\varphi }_0\left\{1-\text{tanh}\left(\xi /\text{W}\right)\right\},$(15) where the amplitude, ${\varphi }_0$, and the width, $\text{W}$, of a single ULF shock wave are given by ${\text{v}}_0/\text{A}$ and $2\text{B}/{\text{v}}_0$, respectively. In addition, one can obtain the electric field, E, by the following equation [29,33]: (16) $E=-d{\varphi }^{\left(1\right)}/d\xi =\left(v_0^2/2AB\right)\sec h^2\left(\xi /W\right).$(16)

3. Overtaking collisions of ULF multi-shock waves

Now to analyse the characteristics of the overtaking collision of ULF shock waves, the Cole–Hopf transformation and the exponential function are utilized to obtain ULF multi-shock wave solutions [37]. Taking the help of the transformations $\tau \to T,\zeta \to -\sqrt{B}X$ and ${\varphi }^{\left(1\right)}\to -\sqrt{B}\mathrm{\Phi }/A$, we can transform Equation (13) to the standard BE equation (17) $\frac{\mathrm{\partial }\mathrm{\Phi }}{\mathrm{\partial }\text{T}}+\mathrm{\Phi }\frac{\mathrm{\partial }\mathrm{\Phi }}{\mathrm{\partial }\text{X}}=\frac{{\mathrm{\partial }}^2\mathrm{\Phi }}{\mathrm{\partial }{\text{X}}^2}.$(17) Then, the standard BE equation (i.e. Equation (17)) is reduced to a linear heat equation by using the Cole–Hopf transformation [37], namely (18) $\mathrm{\Phi }=-2(\log \mathrm{\Psi }{)}_X.$(18) Then, we can obtain the following equation: (19) ${\mathrm{\Psi }}_T-{\mathrm{\Psi }}_{XX}=0.$(19) In what follows, we consider the derivatives to be denoted by lower-case subscript $X$ and $T$. It is well known that a simple solution to the heat equation (i.e. Equation (19)) can be expressed as (20) ${\mathrm{\Psi }}_i={\alpha }_i{e}^{\left(k_{i}X-{\omega }_{i}T\right)}.$(20) Here, the subscript i is a positive integer (i.e. i  = 1,2,3, … ,N), $k_i$ is the wavenumber and ${\omega }_i$ is the frequency. Then, the general solution to the heat equation can be expressed by the following linear superposition: (21) $\mathrm{\Psi }={\alpha }_0+\sum _{i=1}^N{\alpha }_i{e}^{\left(k_{i}X-{\omega }_{i}T\right)},$(21) where ${\alpha }_0\text{and}{\alpha }_i$ are the arbitrary constants. Directly, we can employ the rational exponential function to obtain both the single and multi-shock wave solutions of Equation (13) [36]. First of all, let us examine the single ULF shock wave solution of Equation (17) is given by [36] (22) $\mathrm{\Phi }=\frac{{\alpha }_1{k}_1{e}^{\left(k_{1}X-{\omega }_{1}T\right)}}{{\alpha }_0+{\alpha }_1{e}^{\left(k_{1}X-{\omega }_{1}T\right)}}.$(22) After a few algebraic steps, the linear dispersion relation of Equation (17) $\left(\text{i}.\text{e}.{\omega }_1=-k_1^2\right)$ can be obtained. Then the analytical single ULF shock wave solution of Equation (13) is expressed as [36] (23) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\frac{{\alpha }_1{k}_1{e}^{\left(\frac{-k_1}{\sqrt{B}}\zeta +k_1^2\tau \right)}}{{\alpha }_0+{\alpha }_1{e}^{\left(\frac{-k_1}{\sqrt{B}}\zeta +k_1^2\tau \right)}}.$(23) In addition, to get the two-overtaking ULF shock wave structures, the following rational exponential function is considered [36]: (24) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\begin{array}{c}\sum _{i=1}^2\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)\\ +{\alpha }_{12}\left(k_1+k_2\right){\alpha }_1{\alpha }_2\\ e^{\left(\sum _{i=1}^2\left(\frac{-k_i}{\sqrt{B}}\zeta \right)-\sum _{i=1}^2\left({\omega }_i\tau \right)\right)}\end{array}}{\begin{array}{c}{\alpha }_0+\sum _{i=1}^2\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)\\ +{\alpha }_{12}{\alpha }_1{\alpha }_2{e}^{\left(\sum _{i=1}^2\left(\frac{-k_i}{\sqrt{B}}\zeta \right)-\sum _{i=1}^2\left({\omega }_i\tau \right)\right)}\end{array}}\right].$(24) Using Equation (24) into Equation (13) and equating the coefficients of different power of exponential functions equal to zero, we get the three following cases: Case I: ${\omega }_1=-k_1^2;{\omega }_2=-k_2^2;{\alpha }_{12}=0$, the analytical solution of two-overtaking ULF shock wave of BE is given by [36] (25) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\sum _{i=1}^2\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}{{\alpha }_0+\sum _{i=1}^2\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}\right].$(25) Case II: ${\alpha }_0=0;{\omega }_2={\omega }_1+k_1^2-k_2^2;{\alpha }_{12}=0$. Then analytical solution of the two-overtaking ULF shock wave is written by [36] (26) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\sum _{i=1}^2\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)}{\sum _{i=1}^2\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)}\right].$(26) Case III: ${\alpha }_0=0;{\omega }_1=-k_1^2-2k_1{k}_2;{\omega }_2=-k_2^2-2k_1{k}_2$ and the two-overtaking ULF shock wave reads [36] (27) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\begin{array}{c}\sum _{i=1}^2\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)\\ +{\alpha }_{12}\left(k_1+k_2\right){\alpha }_1{\alpha }_2\\ e^{\left(\sum _{i=1}^2\left(\frac{-k_i}{\sqrt{B}}\zeta \right)-\sum _{i=1}^2\left({\omega }_i\tau \right)\right)}\end{array}}{\begin{array}{c}\sum _{i=1}^2\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta -{\omega }_i\tau \right)}\right)\\ +{\alpha }_{12}{\alpha }_1{\alpha }_2{e}^{\left(\sum _{i=1}^2\left(\frac{-k_i}{\sqrt{B}}\zeta \right)-\sum _{i=1}^2\left({\omega }_i\tau \right)\right)}\end{array}}\right].$(27) In the model at hand, due to the obtained linear dispersion relation $\left(\text{i}.\text{e}.,{\omega }_1=-k_1^2\right)$, we will focus on the analytical solution of BE of the two-overtaking ULF shock wave in the first case (i.e. case I) and ignore, for simplicity, the cases II and III. Following the same way, the analytical solution of the three-overtaking ULF shock wave of BE is written by [36] (28) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\sum _{i=1}^3\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}{{\alpha }_0+\sum _{i=1}^3\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}\right].$(28) In general, we then rewrite the analytical solution of overtaking collisions between ULF multi-shock waves in the following mathematical expression [36]: (29) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left[\frac{\sum _{i=1}^N\left({\alpha }_i{k}_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}{{\alpha }_0+\sum _{i=1}^N\left({\alpha }_i{e}^{\left(\frac{-k_i}{\sqrt{B}}\zeta +k_i^2\tau \right)}\right)}\right].$(29) In the model under consideration, based on the above discussion, ULF multi-shock waves are just a superposition of each other for all times, and it follows that there may not be a phase shift, because all ULF multi-shock waves are thus unaffected by the collision. Of course, we can put ${\alpha }_0={\alpha }_i=1.$ Therefore, let us now rewrite the analytical solution of the two-overtaking ULF shock wave of BE in the following mathematical form: (30) ${\varphi }^{\left(1\right)}=\frac{2\sqrt{B}}{A}\left\{\frac{{\alpha }_1{k}_1{e}^{{\theta }_1}+{\alpha }_2{k}_2{e}^{{\theta }_2}}{\left({\alpha }_0+\left({\alpha }_1{e}^{{\theta }_1}+{\alpha }_2{e}^{{\theta }_2}\right)\right)}\right\},$(30) where ${\theta }_{1,2}\left(=\frac{-k_{1,2}}{\sqrt{B}}\zeta +k_{1,2}^2\tau \right)$ is the notation that contains the linear dispersion law, ${\omega }_{1,2}=-k_{1,2}^2$, describing the BE. Asymptotically, for the condition $\tau >>1,$ the two-overtaking ULF shock wave solution (i.e. Equation (30)) can be expressed as a superposition of two single-ULF shock wave solution (31) ${\varphi }^{\left(1\right)}\approx \frac{2\sqrt{B}}{A}\left(\frac{k_1}{\left(1+e^{-{\theta }_1}\right)}+\frac{k_2}{\left(1+e^{-{\theta }_2}\right)}\right).$(31) We can apply the following identity: (32) $1/\left(1+e^{-x}\right)=\frac{1}{2}\left(1+\tanh \left(\frac{x}{2}\right)\right),$(32) after a bit of manipulations, the asymptotic solution of Equation (13) can be given by (33) ${\varphi }^{\left(1\right)}\approx \sum _{i=1}^2\left\{{\varphi }_i^{\left(0\right)}\left[1-\tanh \left(\frac{k_i}{2B}\left(\zeta -B{k}_i\tau \right)\right)\right]\right\}.$(33) Here, the amplitudes of two single-ULF shock waves due to overtaking collisions are given by the following form: ${\varphi }_i^{\left(0\right)}\left(=k_i\sqrt{B}/A\right)$. From Equation (33), we are clearly dealing with the superposition of two single-ULF shock waves moving in the same direction. In addition, the electric field, E, can be expressed by “sech squared” solitons (34) $E=\sum _{i=1}^2\left\{\left(k_i^2/2A\sqrt{B}\right)\sec h^2\left(\frac{k_i}{2B}\left(\zeta -B{k}_i\tau \right)\right)\right\}.$(34) Thus we can apply the same technique to investigate the overtaking interactions between ULF multi-shock waves. We then rewrite, respectively, the general structures of ULF multi-shock waves and E in the following form: (36) $\begin{array}{rl}{\varphi }^{\left(1\right)}& \approx \sum _{i=1}^N\left\{{\varphi }_i^{\left(0\right)}\left[1-\tanh \left(\frac{k_i}{2B}\left(\zeta -B{k}_i\tau \right)\right)\right]\right\},\end{array}$(36) (37) $\begin{array}{rl}E& =\sum _{i=1}^N\left\{\left(3k_i^2/4A\sqrt{B}\right)\sec h^2\left(\frac{k_i}{2B}\left(\zeta -B{k}_i\tau \right)\right)\right\}.\end{array}$(37)

Figure 1. The overtaking collision profiles between (a) two single-E and (b) two single-ULF shock waves for ultra-relativistic case ${\gamma }_e={\gamma }_{\ell }=4/3$, (c) two single-E and (d) two single-ULF shock waves for non-relativistic case ${\gamma }_e={\gamma }_{\ell }=5/3$ for $\alpha =0.66,$ $\eta$ = 0.01, $k_1=0.8$, and$k_2=1.$

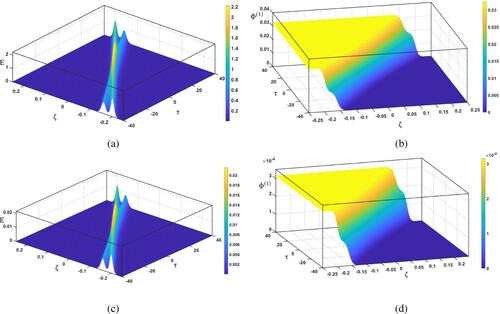
Figure 2. The overtaking collision profiles between (a) three single-E and (b) three single-ULF shock waves for ultra-relativistic case ${\gamma }_e={\gamma }_{\ell }=4/3$, (c) three single-E and (d) three single-ULF shock waves for non-relativistic case ${\gamma }_e={\gamma }_{\ell }=5/3$ for $\alpha =0.66,$ $\eta$ = 0.01, $k_1=0.8$, $k_2=1$ and $k_3=\mathrm{1.2.}$

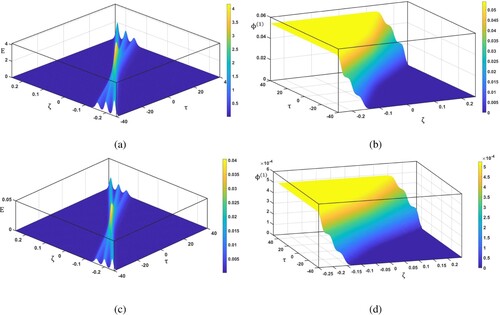
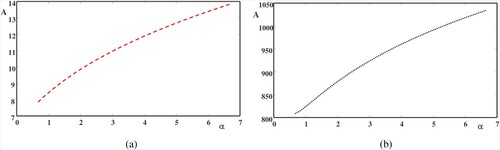
Figure 3. The nonlinear coefficient A (a) for ultra-relativistic case ${\gamma }_e={\gamma }_{\ell }=4/3$ and (b) for non-relativistic case ${\gamma }_e={\gamma }_{\ell }=5/3$.

Figure 4. The overtaking collision profile between (a) two single-ULF shock waves for ultra-relativistic case ${\gamma }_e={\gamma }_{\ell }=4/3$ and (b) two single-ULF shock waves for non-relativistic case ${\gamma }_e={\gamma }_{\ell }=5/3$ for different values of $\alpha$ at $\eta$ = 0.01, $k_1=0.8$ and $k_2=1$.

Figure 5. The overtaking collision profile between (a) three single-ULF shock waves for ultra-relativistic case ${\gamma }_e={\gamma }_{\ell }=4/3$ and (b) three single-ULF shock waves for non-relativistic case ${\gamma }_e={\gamma }_{\ell }=5/3$ for different values of $\eta$ at $\alpha =0.66$, $k_1=0.8$, $k_2=1$ and $k_3=\mathrm{1.2.}$

4. Numerical simulation and discussion

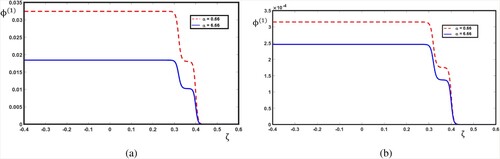
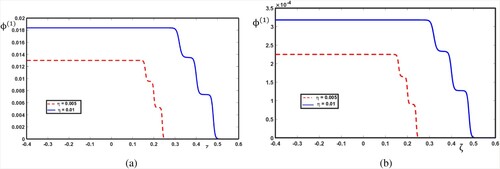
In this section, we numerically examine the physical nature of ULF multi-shock waves and the electric field, E, due to the overtaking collision at different times. In addition, we will study the effects of the light-to-heavy ion density ratio, α, and the heavy-ion kinematic viscosity, η, on the amplitude and the steepness of ULF multi-shock waves during the overtaking phenomenon. Interestingly, we will focus on the study of the overtaking interaction between two/three single-ULF shock waves/E propagating in the same direction and having different amplitudes. Using the numerical data of white dwarf stars is instructive [29,30,33]. The densities of electrons and light nuclei are $n_s^{\left(0\right)}\cong {10}^{29}-{10}^{31}\text{c}{\text{m}}^{-3}$, which must satisfy the quasi-neutrality condition. Figures 1 and 2 show, respectively, the variations of two and three single-E/ULF shock waves profiles against the space coordinate $\zeta$ and the time variable $\tau$ in two cases (i.e. ultra-relativistic and non-relativistic degenerate plasmas cases). First, for the ultra-relativistic case, Figure 1(a) illustrates that two electric fields (solitons), E, move in the same direction, approach each other, collide and asymptotically separate away. When two solitons overtake, a new nonlinear wave is produced during their overtaking collision, which moves ahead of the colliding solitons; both its amplitude and width are larger than those of colliding solitons. Figure 1(b) demonstrates the variation of two single-ULF shock waves with the space coordinate $\zeta$ and time $\tau$. Moreover, we note, in Figure 1(b), the evolution in the profile of the progressive two single-ULF shock waves before (time < 0), during (time = 0) and after (time > 0) the overtaking phenomenon. Second, it is highly interesting to examine the features of non-relativistic degenerate plasmas, similar behaviour is observed as seen for ultra-relativistic degenerate plasmas, for two solitons and two single-ULF shock waves as shown in Figure 1(c and d), respectively. In a similar manner, for three solitons and three single-ULF shock waves, Figure 2(a and b) (for ultra-relativistic case) and Figure 2(c and d) (for non-relativistic case) illustrate the same behaviour as in the case of Figure 1(a–d), respectively. It is noteworthy that the amplitudes of solitons and ULF shock waves are large for ultra-relativistic degenerate plasmas. Figure 3(a and b) show a comparison among the nonlinear coefficient, A, for the ultra-relativistic case and non-relativistic case, respectively. The nonlinear coefficient increases with the increase in the light-to-heavy ion density ratio, α. In addition, the nonlinear coefficient, A, is large for the non-relativistic case. Here, we address the question of how the light-to-heavy ion density ratio, α, and the heavy-ion kinematic viscosity, η, affect the dynamic behaviour of two/three single-ULF shock waves. In all cases, it is clear from Figure 4 that the amplitude and the steepness of two single-ULF shock waves increase with decreasing the values of the light-to-heavy ion density ratio. Physically this means that increasing α leads to a decrease of the propagation speed, which in turn leads to an increase of the nonlinear coefficient A as shown in Figure 3. This increase in the nonlinear coefficient causes decreases in the strength of two single-ULF shock waves. Figure 5(a and b) show how the physical behaviour of the three single-ULF shock waves varies with the variation of the heavy-ion kinematic viscosity, η. From Figure 4, with increasing the heavy-ion kinematic viscosity, the amplitude and the steepness of three single-ULF shock waves increase for both cases (ultra-relativistic case and non-relativistic case). From a physical point of view, this is essentially because the Burgers term in the BE is caused by the heavy-ion kinematic viscosity. Therefore, the presence of kinematic viscosity among the plasma constituents actually increases the Burgers term, which in turn leads to the enhancement of strength and steepness of the three single-ULF shock waves. It is interesting to compare our results with previous studies. The present finding, without inertialess degenerate light ion fluid, exactly agrees with the earlier study by Zobaer et al. [29]. In addition, the results of Islam et al. [33] are in agreement with the present results for the single-ULF shock wave, except that the shock wave amplitude in Ref. [33] is independent of η.

In this work, we have studied the propagation and overtaking interactions of ULF multi-shock waves in non-relativistic and ultra-relativistic degenerate plasmas. From the governing equations, the BE has been derived to describe the propagation of ULF shock waves. In addition, we derived ULF multi-shock wave solutions using Cole–Hopf transformation and the exponential function. Finally, we have discussed ULF multi-shock waves dynamics, such as the two/three single-ULF shock waves, together with the physical parameters of the physical model at hand (i.e. the light-to-heavy ion density ratio and the heavy-ion kinematic viscosity). It was observed that the physical nature of two/three single-ULF shock waves is modified by the heavy-ion kinematic viscosity, which is the key requirement for the existence of ULF shock waves. It is also seen that the light-to-heavy ion density ratio has modified the amplitudes of ULF multi-shock waves, which is one of the important results of this work. Lastly, we believe that the present study may be helpful in understanding the propagation of ULF shock waves in white dwarfs where inertial mobile heavy-ion fluid, inertialess light ions and electrons are present.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a research groups program under grant number KKU R.G.P.1/239/41. The authors also thank the editor and his staff for their kind cooperation.

Disclosure statement

No potential conflict of interest was reported by the author(s).