Instability of opposite polarity charged dusty plasma with vortex-like distributed electrons

Abstract

Electrons in space plasma may follow vortex-like distribution, that is why we have derived the three-dimentional (3D) nonlinear modified Zakharov–Kuznetsov (mZK), describing the propagation of dust acoustic solitary to the plasma system composed of four components, magnetized charged dust plasma with electrons modelled by vortex-like distribution. By using the reductive perturbation method, it has been found that both solitary wave amplitude and width are affected by the plasma parameters: graim charge ratio ρ, population parameter β, and temperature ratio σ. The small-k perturbation technique has also been applied to study the instability criterion and growth rate of this instability. Cyclotron frequency Ω, temperature ratio ${\sigma }_d$, direction cosine (${\iota }_{\eta }$ and ${\iota }_{\zeta }$), and grain charge ratio ρ are found to modify the instability growth rate Γ.

Keywords:

• DA waves
• mZK equation
• wave instability
• vortex-like electrons

1. Introduction

The existence of dust charged particles has been noticed widely not only in space plasma (cometary tails, interstellar media, Earth ionosphere, planetary atmospheres, etc.) but also in laboratory [1–5]. Recently, dust has also been observed in Hall thrusters [6, 7]. The dynamics of nonlinear waves are found to have an increasingly important role in grasping the behaviour of multicomponents dusty plasma [8–10]. The nonlinear and linear properties of one dimensional dust acoustic (DA) waves in coupled unmagnetized dusty plasmas have been investigated by many researchers [11, 12]. Malik et al. [13] have studied small amplitude DA solitary solution in two ion temperature magnetized plasma. ElWakil et al. [14] have used the reductive perturbation technique to get the Zakharov Kuznetsov (ZK) equation representing the propagation of nonlinear small but finite amplitude DA waves in magnetized collisionless dusty plasma. El-Tantawy et al. [15] have studied the nonlinear ion acoustic waves in a magneto plasma consisting of nonextensive distributed positrons, non-Maxellian electrons and cold ion fluid. Zaghbeer et al. [16] have theoretically studied the effect of nonextensive electron and ion on DA rogue waves in dusty plasma of opposite polarity. Dusty plasma mainly supports two categories of acoustic waves: low frequency DA waves containing mobile dust particles and high frequency dust–ion acoustic (DIA) waves containing static dust particles and mobile ions [17]. Both of these wave modes have been investigated experimentally [18] and theoretically [19–21]. The existence of DA waves was first theoretically predicted by Rao et al. [22], with the inertia introduced by the dust particles and the restoring force introduced by the pressure of inertialess electrons and ions. Particles in thermodynamic equilibrium systems are described by Maxwellian distribution. However, laboratory, astrophysical and space plasma systems are found to be in a quasi steady state so particles such as electron and ions will deviate from Maxwellian distribution [23]. The trapping of electrons is noticed in some laboratory plasma experiments as well as in space plasmas [24, 25]. Hot electrons in most space plasmas follow the vortex-like distribution as a result of hot electrons trapping in the wave potential caused by phase space holes [26]. On the other hand, laboratory experiments, diffraction limited laser–plasma interaction experiment where the low velocity wave corresponding to stimulated scattering from electron acoustic (EA) waves causes strong electron trapping, are noticed [27]. The wave propagation in the plasma system containing trapped/vortex-like electron distribution has been discussed by many authors. Mamun and Shukla [28] have derived the modified Korteweg–de Vries (mKdV) equation in collisionless plasma consisting of stationary ions, hot electrons modelled by vortex-like distribution and cold electron fluid. It has been shown that the EA solitary wave amplitude increases as the temperature of the trapped electron increases, but their width decreases. They also compared their results with the most noticeable features of the broad band electrostatic noise in the dayside auroral zone. Later on, Elwakil et al. [29] have considered the solitary EA wave propagation in an unmagnetized collisionless plasma consisting of hot electrons modelled by vortex-like distribution, cold electron fluid and stationary ions, They have mathematically obtained higher-order solutions and have confirmed that these solutions in consistency with the original equation numerical solution. Recently, the study of wave solution of ZK equation and the coexistence of wave instability have been approached [30–37]. Shalaby et al. [38] have analysed the 3D instability of DIA solitary waves using the small-k expansion method. Their results showed that the propagation angle, nonisothermal electrons temperature, and external magnetic field strongly affect the criterion of the instability as well as the growth rate of this instability. Zaghbeer et al. [39] have theoretically studied wave instability features in a collisionless magnetized dusty plasma system containing positively and negatively charged dusty particles, and they have found in that nonextensive parameter, the grain charge mass ratio and cyclotron frequency strongly modify the wave properties of the DA waves as well as the instability growth rate.

In this paper, DA solitary wave propagation have been investigated in a magnetized dusty plasma consisting of opposite polarity charged dust grains, trapped electrons modelled by vortex-like distribution and Maxwellian ion distribution. Using the reductive perturbation method [40], we have derived mZK equation which is also known as mKdV equation in three dimension and its solution. We have also studied instability criterion and the growth rate. The outline of this paper is as follows. In Section 2, the basic equations representing the system are presented. In Section 3, mZK equation representing DA solitary wave propagation is derived. The instability analysis and the growth rate are computed in Section 4. Finally, conclusion is given in Section 5.

2. Governing system

In this system, we consider a collisionless magnetized dusty plasma consisting of four components, namely: negative cold dust grains, positive charged warm adiabatic dust grains, vortex-like electron distribution, and Maxwellian ion distribution [41, 42]. The properties of  DA solitary waves in a magnetized plasma with external magnetic field $B_0=\overrightarrow{e_z}{B}_0$ (where $\overrightarrow{e_z}$ is a unit vector in the z direction) can be depicted by the following normalized 3D fluid equations. For positive dust grains, (1) $\begin{array}{rl}& \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\mathit{▽}\mathbf{\cdot }(n\mathbf{u})=0,\end{array}$(1) (2) $\begin{array}{rl}& \rho (\frac{\mathrm{\partial }\mathbf{u}}{\mathrm{\partial }t}+(\mathbf{u}\mathbf{.}\mathit{▽}\mathbf{)}u)+\mathit{▽}\mathit{\varphi }+\frac{{\sigma }_d}{n}\mathit{▽}\mathit{p}-(\mathit{u}\mathbf{\times }\mathrm{\Omega }\overrightarrow{e_z})=0,\end{array}$(2) (3) $\begin{array}{rl}& \frac{\mathrm{\partial }\mathit{p}}{\mathrm{\partial }t}+(\mathit{u}\mathbf{.}\mathit{▽})\mathit{p}+\gamma \mathit{p}(\mathit{▽}\mathbf{.}\mathit{u})=0.\end{array}$(3) For negative dust grains, (4) $\begin{array}{rl}& \frac{\mathrm{\partial }N}{\mathrm{\partial }t}+\mathit{▽}\mathbf{\cdot }(N\mathbf{v})=0,\end{array}$(4) (5) $\begin{array}{rl}& \frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }t}+(\mathbf{v}\mathbf{.}\mathit{▽})\mathbf{v}-\mathit{▽}\mathit{\varphi }+(\mathbf{v}\mathbf{\times }\mathrm{\Omega }\overrightarrow{e_z})=0.\end{array}$(5) Here, the quantities n, N (u, v) denote the perturbed densities (velocities) of positive and negative dusty grains and their corresponding equilibrium values are $n_0,N_0$. We have defined the quantities: $\rho =Z_n{m}_1/Z_p{m}_2$, $Z_p(Z_n)$ is the charges of the positive (negative) dust particles, $m_1(m_2)$ is the mass of the positive (negative) dust particles, $k_B$ is the Boltzmann constant, $T_p(T_i)$ is the the positive dust (ion) temperature, ${\sigma }_d=(T_p/T_i{Z}_p),\sigma =(T_e/T_i),\mu =(\frac{n_0{Z}_p}{N_0{Z}_n})$, and ${\mu }_e=(\frac{n_{e0}}{N_0{Z}_n})$, ${\mu }_i=(\frac{n_{i0}}{N_0{Z}_n})$. $\mathit{\varphi }$ represents the electrostatic potential, $\mathit{p}$ is the thermal positive grains fluid pressure, and Ω is the dust cyclotron frequency.

Poisson equation reads (6) ${▽}^2\mathit{\varphi }=N-\mu n+{\mu }_e{n}_e-{\mu }_i{n}_i,$(6) where $n_e(n_i)$ is the electron (ion) density. Electrons are modelled by vortex-like distribution so we can write electron density $n_e$ as [43] (7) $n_e=I(\varphi )+\frac{2}{\sqrt{-\pi \beta }}{W}_D(\sqrt{-\beta \varphi }),$(7) where $I(\varphi )$ and $W_D$ can be defined as $\begin{array}{rl}I(\varphi )& =[1-erf(\sqrt{\varphi })]\exp (\varphi ),\\ W_D(\varphi )& =\exp (-{\varphi }^2){\int }_0^{\varphi }\exp y^2\mathrm{d}y,\end{array}$where $erf(\varphi )$ is the error function. In case $\varphi <<1$, Equation (7(7) $n_e=I(\varphi )+\frac{2}{\sqrt{-\pi \beta }}{W}_D(\sqrt{-\beta \varphi }),$(7) ) gives (8) $\begin{array}{rl}{n}_e& =1+\sigma \varphi -\frac{4(1-\beta )}{3\sqrt{\pi }}{\sigma }^{3/2}{\varphi }^{3/2}+\frac{1}{2}{\sigma }^2{\varphi }^2\\ & -\frac{8}{15\sqrt{\pi }}(1-{\beta }^2){\sigma }^{5/2}{\varphi }^{5/2}+\frac{{\sigma }^3{\varphi }^3}{6}+\cdots \cdots \cdots ,\end{array}$(8) where $n_e(n_i)$ is the electron (ion) density. The electron density is expressed in Equation (8(8) $\begin{array}{rl}{n}_e& =1+\sigma \varphi -\frac{4(1-\beta )}{3\sqrt{\pi }}{\sigma }^{3/2}{\varphi }^{3/2}+\frac{1}{2}{\sigma }^2{\varphi }^2\\ & -\frac{8}{15\sqrt{\pi }}(1-{\beta }^2){\sigma }^{5/2}{\varphi }^{5/2}+\frac{{\sigma }^3{\varphi }^3}{6}+\cdots \cdots \cdots ,\end{array}$(8) ) by vortex-like distribution representing the trapping of hot electrons caused by the existence of phase space holes, where $|\beta |=\frac{T_h}{T_{ht}}$ is the ratio of the free hot electron temperature $T_h$ to the hot trapped electron temperature $T_{ht}$. It is obvious from Equation (8(8) $\begin{array}{rl}{n}_e& =1+\sigma \varphi -\frac{4(1-\beta )}{3\sqrt{\pi }}{\sigma }^{3/2}{\varphi }^{3/2}+\frac{1}{2}{\sigma }^2{\varphi }^2\\ & -\frac{8}{15\sqrt{\pi }}(1-{\beta }^2){\sigma }^{5/2}{\varphi }^{5/2}+\frac{{\sigma }^3{\varphi }^3}{6}+\cdots \cdots \cdots ,\end{array}$(8) ) that when ever $\beta =1$ the electron density distribution is reduced to the well known Maxwellian distribution, In case of values of β $<0$, a vortex-like excavated trapped electron distribution corresponding to an under population of trapped electrons, which is the case of our interest here.The ion density $n_i$ is described by (9) $n_i=\exp (-\varphi ).$(9) The velocities u and v are normalized by the the characteristic speed $Cs=\surd \rho V_T$, where $V_T=(Z_p{k}_B{T}_i/m_1{)}^{\frac{1}{2}}$. The quantity ϕ is normalized by $k_B{T}_i/e$. Space x and time t have been normalized by (negative dust plasma Debye length) ${\lambda }_D=(k_B{T}_i/4\pi N_0{Z}_n{e}^2{)}^{\frac{1}{2}}$ and (negative dust plasma frequency) ${\omega }_p^{-1}=(m_2/4\pi N_0{Z}_n^2{e}^2{)}^{\frac{1}{2}},p$ is normalized by $n_0{k}_B{T}_p$.

To discuss mZK (modified Zakharov–Kuznetsov) equation in 3D, we use the stretched coordinates, (10) $\tau ={ϵ}^{\frac{3}{2}}t,X={ϵ}^{\frac{1}{4}}x,Y={ϵ}^{\frac{1}{4}}y,Z={ϵ}^{\frac{1}{4}}(z-\lambda t),$(10) where ϵ measures the size of the perturbation amplitude and λ is the soliton phase speed. Expanding the parameters in Equations (1(1) $\begin{array}{rl}& \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\mathit{▽}\mathbf{\cdot }(n\mathbf{u})=0,\end{array}$(1) )–( 9(9) $n_i=\exp (-\varphi ).$(9) ) about equilibrium values as (11) $\begin{array}{rl}\left(\begin{array}{c}n\\ N\\ P\\ \varphi \end{array}\right)& =\left(\begin{array}{c}1\\ 1\\ 1\\ 0\end{array}\right)+\sum _{l=1}^{\mathrm{\infty }}\left(\begin{array}{c}{ϵ}^l{n}_l\\ {ϵ}^{l}Nl\\ {ϵ}^l{P}_l\\ {ϵ}^l{\varphi }_l\end{array}\right),\end{array}$(11) (12) $\begin{array}{rl}\left(\begin{array}{c}{u}_{x,y}\\ v_{x,y}\\ u_z,v_z\end{array}\right)& =\sum _{l=1}^{\mathrm{\infty }}\left(\begin{array}{c}{ϵ}^{1+l/2}{u}_{xl,yl}\\ {ϵ}^{1+l/2}{v}_{xl,yl}\\ {ϵ}^l{u}_{zl},v_{zl}\end{array}\right).\end{array}$(12) Charge neutrality condition reads (13) $1-{\mu }_i-\mu +{\mu }_e=0.$(13) The boundary conditions are given by $\left|\xi \right|\to \mathrm{\infty },n=N=1,p=1,u=v=0,\varphi =0.$Substituting Equations (10(10) $\tau ={ϵ}^{\frac{3}{2}}t,X={ϵ}^{\frac{1}{4}}x,Y={ϵ}^{\frac{1}{4}}y,Z={ϵ}^{\frac{1}{4}}(z-\lambda t),$(10) )–( 12(12) $\begin{array}{rl}\left(\begin{array}{c}{u}_{x,y}\\ v_{x,y}\\ u_z,v_z\end{array}\right)& =\sum _{l=1}^{\mathrm{\infty }}\left(\begin{array}{c}{ϵ}^{1+l/2}{u}_{xl,yl}\\ {ϵ}^{1+l/2}{v}_{xl,yl}\\ {ϵ}^l{u}_{zl},v_{zl}\end{array}\right).\end{array}$(12) ) in Equations (1(1) $\begin{array}{rl}& \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\mathit{▽}\mathbf{\cdot }(n\mathbf{u})=0,\end{array}$(1) )–( 9(9) $n_i=\exp (-\varphi ).$(9) ), collecting the coefficient of like powers in ϵ, we get the first-order equations as (14) $\begin{array}{rl}& n_1=\frac{{\varphi }_1}{\chi },u_{x_1}=-\frac{{\lambda }^2\rho }{\chi \mathrm{\Omega }}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }Y},\\ & u_{y_1}=\frac{{\lambda }^2\rho }{\chi \mathrm{\Omega }}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }X},\\ & u_{z_1}=\frac{\lambda }{\chi }{\varphi }_1,\\ & p_1=\frac{\gamma }{\chi }{\varphi }_1,\\ & N_1=\frac{-{\varphi }_1}{{\lambda }^2},v_{x_1}=-\frac{1}{\mathrm{\Omega }}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }Y},\\ & v_{y_1}=\frac{1}{\mathrm{\Omega }}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }X},v_{z_1}=-\frac{{\varphi }_1}{\lambda },\\ & (\frac{\mu }{\chi }+\frac{1}{{\lambda }^2}-\sigma {\mu }_e-{\mu }_i)=0,\end{array}$(14) where $\chi =({\lambda }^2\rho -\gamma {\sigma }_d)$.

Next order in ϵ for positive dust gives (15) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{n}_2}{\mathrm{\partial }Z}+\frac{\mathrm{\partial }{u}_{x_2}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{y_2}}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{u}_{z_2}}{\mathrm{\partial }Z}=0,\\ & -\lambda \rho \frac{\mathrm{\partial }{u}_{z_2}}{\mathrm{\partial }Z}+\rho \frac{\mathrm{\partial }{u}_{z_1}}{\mathrm{\partial }\tau }+{\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Z}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }Z}=0,\\ & {\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }Y}-\lambda \rho \frac{\mathrm{\partial }{u}_{y2}}{\mathrm{\partial }Z}=0,\\ & {\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }X}-\lambda \rho \frac{\mathrm{\partial }{u}_{x2}}{\mathrm{\partial }Z}=0,\\ & \frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Z}+\gamma (\frac{\mathrm{\partial }{u}_{x2}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{y2}}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{u}_{z2}}{\mathrm{\partial }Z})=0,\\ & u_{y2}=\frac{{\lambda }^3{\rho }^2}{\chi {\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }Y\mathrm{\partial }Z},\\ & u_{x2}=\frac{{\lambda }^3{\rho }^2}{\chi {\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }X\mathrm{\partial }Z}.\end{array}$(15) Next order in ϵ for negative dust gives (16) $\begin{array}{rl}& \frac{\mathrm{\partial }{N}_1}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{N}_2}{\mathrm{\partial }Z}+\frac{\mathrm{\partial }{v}_{x_2}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{v}_{y_2}}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{v}_{z_2}}{\mathrm{\partial }Z}=0,\\ & \frac{\mathrm{\partial }{v}_{z1}}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{v}_{z_2}}{\mathrm{\partial }Z}-\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }Z}=0,\\ & v_{x_2}=-\frac{\lambda }{{\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }X\mathrm{\partial }Z},\\ & v_{y_2}=-\frac{\lambda }{{\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }Y\mathrm{\partial }Z}.\end{array}$(16) Poisson equation gives (17) $\begin{array}{rl}& \mu n_2-N_2+\frac{4\sigma {\mu }_e}{3\sqrt{\pi }}(1-\beta ){\varphi }_1^{3/2}-(\sigma {\mu }_e-{\mu }_i){\varphi }_2\\ & +\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Z}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Y}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{X}^2}=0.\end{array}$(17) Eliminating quantities $n_2,u_2,N_2,{\nu }_2$, and ${\varphi }_2$ in Equations (15(15) $\begin{array}{rl}& \frac{\mathrm{\partial }{n}_1}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{n}_2}{\mathrm{\partial }Z}+\frac{\mathrm{\partial }{u}_{x_2}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{y_2}}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{u}_{z_2}}{\mathrm{\partial }Z}=0,\\ & -\lambda \rho \frac{\mathrm{\partial }{u}_{z_2}}{\mathrm{\partial }Z}+\rho \frac{\mathrm{\partial }{u}_{z_1}}{\mathrm{\partial }\tau }+{\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Z}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }Z}=0,\\ & {\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }Y}-\lambda \rho \frac{\mathrm{\partial }{u}_{y2}}{\mathrm{\partial }Z}=0,\\ & {\sigma }_d\frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{\varphi }_2}{\mathrm{\partial }X}-\lambda \rho \frac{\mathrm{\partial }{u}_{x2}}{\mathrm{\partial }Z}=0,\\ & \frac{\mathrm{\partial }{P}_1}{\mathrm{\partial }\tau }-\lambda \frac{\mathrm{\partial }{P}_2}{\mathrm{\partial }Z}+\gamma (\frac{\mathrm{\partial }{u}_{x2}}{\mathrm{\partial }X}+\frac{\mathrm{\partial }{u}_{y2}}{\mathrm{\partial }Y}+\frac{\mathrm{\partial }{u}_{z2}}{\mathrm{\partial }Z})=0,\\ & u_{y2}=\frac{{\lambda }^3{\rho }^2}{\chi {\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }Y\mathrm{\partial }Z},\\ & u_{x2}=\frac{{\lambda }^3{\rho }^2}{\chi {\mathrm{\Omega }}^2}\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }X\mathrm{\partial }Z}.\end{array}$(15) )–( 17(17) $\begin{array}{rl}& \mu n_2-N_2+\frac{4\sigma {\mu }_e}{3\sqrt{\pi }}(1-\beta ){\varphi }_1^{3/2}-(\sigma {\mu }_e-{\mu }_i){\varphi }_2\\ & +\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Z}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Y}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{X}^2}=0.\end{array}$(17) ), the mZK equation can be obtained in the form (18) $\begin{array}{rl}& \frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\tau }+AB\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }Z}+\frac{1}{2}A\frac{\mathrm{\partial }}{\mathrm{\partial }Z}\\ & [\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Z}^2}+D(\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{X}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Y}^2})]=0,\end{array}$(18) where (19) $\begin{array}{rl}A& =\frac{2}{\frac{2\lambda \mu \rho }{\chi {}^2}+\frac{2}{{\lambda }^3}},\\ B& =-\frac{(\beta -1)\sigma {\mu }_e}{2\sqrt{\pi }},\\ D& =\frac{({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4\mu {\rho }^3}{2{\mathrm{\Omega }}^2\chi {}^2}.\end{array}$(19)

3. Solitary wave analysis for the mZK equation

To study the propagation of the solitary waves (SWs) in a magnetic field located in the $(Z-X)$ plane, we first rotate the axes $(X-Z)$ by an angle ϑ (angle between propagating wave and Z axis), keeping Y axis fixed. We obtain the new variables, (20) $\begin{array}{rl}& \zeta =X\cos \vartheta -Z\sin \vartheta ,\eta =y,\\ & \xi =X\sin \vartheta +Z\cos \vartheta ,\tau ={\tau }^{\setminus }.\end{array}$(20) Equation (18(18) $\begin{array}{rl}& \frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\tau }+AB\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }Z}+\frac{1}{2}A\frac{\mathrm{\partial }}{\mathrm{\partial }Z}\\ & [\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Z}^2}+D(\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{X}^2}+\frac{{\mathrm{\partial }}^2{\varphi }_1}{\mathrm{\partial }{Y}^2})]=0,\end{array}$(18) ) could be rewritten as (21) $\begin{array}{rl}& \frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }{\tau }^{\setminus }}+R_1\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi }+R_2\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^3}\\ & +R_3\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\zeta }+R_4\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\zeta }^3}\\ & +R_5\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^2\mathrm{\partial }\zeta }+R_6\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\zeta }^2}+R_7\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\eta }^2}\\ & +R_8\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\zeta \mathrm{\partial }{\eta }^2}=0,\end{array}$(21) where (22) $\begin{array}{rl}{R}_1& =AB\cos \vartheta ,\\ R_2& =\frac{1}{2}A({\cos }^2\vartheta +D{\sin }^2\vartheta \cos \vartheta ),\\ R_3& =-AB\sin \vartheta ,\\ R_4& =-\frac{1}{2}A({\sin }^2\vartheta -D{\cos }^2\vartheta \sin \vartheta ),\\ R_5& =A[D(\sin \vartheta {\cos }^2\vartheta -\frac{1}{2}{\sin }^3\vartheta )\\ & -\frac{3}{2}{\cos }^2\vartheta \sin \vartheta ],\\ R_6& =-A[D({\sin }^2\vartheta \cos \vartheta -\frac{1}{2}{\cos }^3\vartheta )\\ & -\frac{3}{2}\cos \vartheta {\sin }^2\vartheta ],\\ R_7& =\frac{1}{2}AD\cos \vartheta ,\\ R_8& =-\frac{1}{2}AD\sin \vartheta .\end{array}$(22) Substitute ${\varphi }_1$ in the form, (23) $\begin{array}{rl}{\varphi }_1& ={\varphi }_o(\mathcal{Z}),\end{array}$(23) (24) $\begin{array}{rl}\mathcal{Z}& =\xi -u_o{\tau }^{\setminus },\end{array}$(24) the steady state form of mZK under transformation (24(24) $\begin{array}{rl}\mathcal{Z}& =\xi -u_o{\tau }^{\setminus },\end{array}$(24) ) becomes (25) $-u_o\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_1\sqrt{{\varphi }_o}\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_2\frac{{\mathrm{\partial }}^3{\varphi }_o}{\mathrm{\partial }{\mathcal{Z}}^3}=0.$(25) Applying boundary conditions: ${\varphi }_1\to 0,(\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}\mathcal{Z}})\to 0,(\frac{d^2{\varphi }^{(1)}}{\mathrm{d}{\mathcal{Z}}^2})\to 0$ at $\mathcal{Z}=\pm \mathrm{\infty }$, the soliton solution is obtained as (26) $\begin{array}{rl}{\varphi }_o(\mathcal{Z})& ={\varphi }_{om}{\mathrm{sech}}^4\kappa \mathcal{Z},\\ {\varphi }_{om}& =\left(\frac{15u_o}{8R_1}\right),\kappa =\frac{1}{4}\sqrt{\frac{u_o}{R_2},}\end{array}$(26) where ${\varphi }_{om}$ is the soliton amplitude and ${\kappa }^{-1}$ is width Δ. The effect of vortex-like electron distribution causes the soliton solution. Equation (26(26) $\begin{array}{rl}{\varphi }_o(\mathcal{Z})& ={\varphi }_{om}{\mathrm{sech}}^4\kappa \mathcal{Z},\\ {\varphi }_{om}& =\left(\frac{15u_o}{8R_1}\right),\kappa =\frac{1}{4}\sqrt{\frac{u_o}{R_2},}\end{array}$(26) ) to be proportional to ${\mathrm{sech}}^4\kappa Z$ instead of ${\mathrm{sech}}^2\kappa Z$ which is the solution for the same system with Maxwellian electron distribution. It is clear from Equation (19(19) $\begin{array}{rl}A& =\frac{2}{\frac{2\lambda \mu \rho }{\chi {}^2}+\frac{2}{{\lambda }^3}},\\ B& =-\frac{(\beta -1)\sigma {\mu }_e}{2\sqrt{\pi }},\\ D& =\frac{({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4\mu {\rho }^3}{2{\mathrm{\Omega }}^2\chi {}^2}.\end{array}$(19) ) that A and B are always positive for all the numerical values allowed for the system parameters. It means that this system supports only the propagation of solitary SWs associated with positive potential. 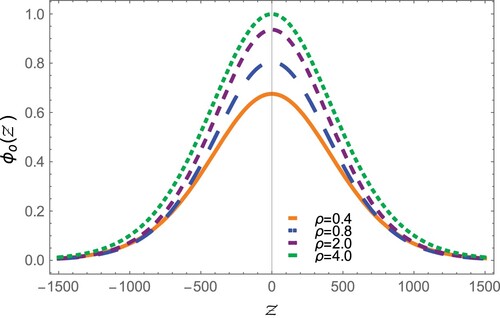This differ from the results found for the same system with nonextensive electron and ion distribution [36] in which compressive (${\varphi }_{om}<0$) and rarefactive (${\varphi }_{om}>0$) soliton could exist depending on the value of grain charge ratio ρ Figure 1 shows that the SWs amplitude ${\varphi }_{om}$ goes higher with increasing the values of ρ which indicates that the net charge of the charged dust grains affects the SWs amplitude but cannot make it negative. The SWs width is found to increase (decrease) with $\rho \gtrsim 1.2$ ($\rho \lesssim 1.2$) as shown in Figure 2. It is obvious from Equations (26(26) $\begin{array}{rl}{\varphi }_o(\mathcal{Z})& ={\varphi }_{om}{\mathrm{sech}}^4\kappa \mathcal{Z},\\ {\varphi }_{om}& =\left(\frac{15u_o}{8R_1}\right),\kappa =\frac{1}{4}\sqrt{\frac{u_o}{R_2},}\end{array}$(26) ), (22(22) $\begin{array}{rl}{R}_1& =AB\cos \vartheta ,\\ R_2& =\frac{1}{2}A({\cos }^2\vartheta +D{\sin }^2\vartheta \cos \vartheta ),\\ R_3& =-AB\sin \vartheta ,\\ R_4& =-\frac{1}{2}A({\sin }^2\vartheta -D{\cos }^2\vartheta \sin \vartheta ),\\ R_5& =A[D(\sin \vartheta {\cos }^2\vartheta -\frac{1}{2}{\sin }^3\vartheta )\\ & -\frac{3}{2}{\cos }^2\vartheta \sin \vartheta ],\\ R_6& =-A[D({\sin }^2\vartheta \cos \vartheta -\frac{1}{2}{\cos }^3\vartheta )\\ & -\frac{3}{2}\cos \vartheta {\sin }^2\vartheta ],\\ R_7& =\frac{1}{2}AD\cos \vartheta ,\\ R_8& =-\frac{1}{2}AD\sin \vartheta .\end{array}$(22) ), and (19(19) $\begin{array}{rl}A& =\frac{2}{\frac{2\lambda \mu \rho }{\chi {}^2}+\frac{2}{{\lambda }^3}},\\ B& =-\frac{(\beta -1)\sigma {\mu }_e}{2\sqrt{\pi }},\\ D& =\frac{({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4\mu {\rho }^3}{2{\mathrm{\Omega }}^2\chi {}^2}.\end{array}$(19) ) that the temperature ratio β ($\frac{T_h}{T_{ht}}$) does not change the width of the solitary waves. However, from Figure 3, the amplitude of the SWs is found to decrease with $|\beta |$. 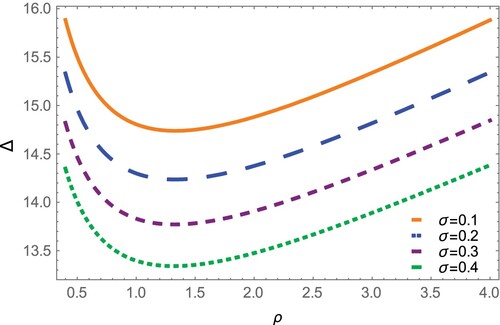It is also clear from Figures 2 and 3 that the width (amplitude) of the SWs decreases (increases) with electrons to ion charge ratio σ. 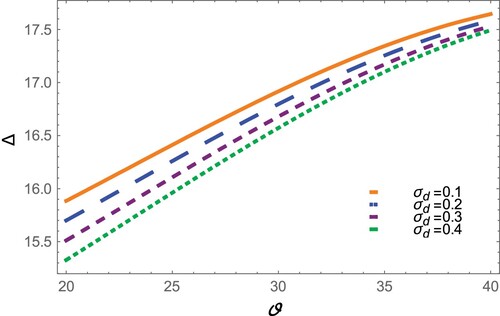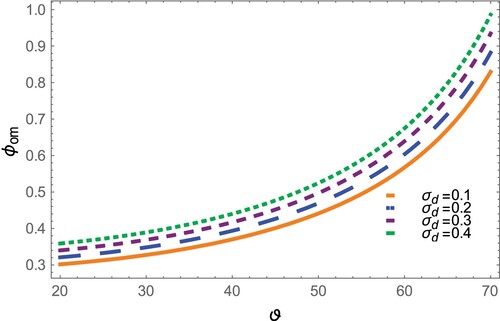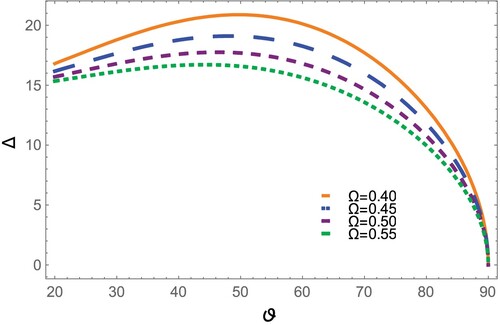It seems from Figures 4 and 5 that as the charge ratio ${\sigma }_d$ $(T_p/T_i{Z}_p)$ increases the SWs width decreases but the amplitude increases. As the dust cyclotron frequency Ω increases, the dispersion effect increases which leads to a decrease in the SWs width, i.e. a stronger magnetic field causes narrower width. The effects of obliqueness angel ϑ on the SWs amplitude and width were illustrated in Figures 5 and 6. It was shown that SWs amplitude increases with ϑ. However, the width is found to increase with ϑ at lower range $({20}^{\circ }--{45}^{\circ })$ but decreases at higher range $({45}^{\circ }--{85}^{\circ })$.

Figure 1. Variation of soliton wave solution ${\varphi }_o(\mathcal{Z})$ with $\mathcal{Z}$ for different values of ρ at $\mathrm{\Omega }=0.5$, $u_o=0.12$, ${\sigma }_d=0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\sigma =0.3$.

Figure 2. Variation of soliton's wave width Δ with ρ for different values of σ at $\mathrm{\Omega }=0.5$, $u_o=0.12$, ${\sigma }_d=0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta ={20}^{\circ }$.

Figure 3. Variation of soliton's wave amplitude ${\varphi }_{om}$ with σ for different values of β at $\mathrm{\Omega }=0.5$, $u_o=0.12$, ${\sigma }_d=0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta ={20}^{\circ }$.

Figure 4. Variation of soliton's wave width Δ with ϑ for different values of ${\sigma }_d$ at $\mathrm{\Omega }=0.5$, $u_o=0.12$, $\sigma =0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\rho =0.4$.

Figure 5. Variation of soliton's wave amplitude ${\varphi }_{om}$ with ϑ for different values of σ at $\mathrm{\Omega }=0.5$, $u_o=0.12$, $\sigma =0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\rho =0.4,\beta =-0.5$.

Figure 6. Variation of soliton's wave width Δ with ϑ for different values of Ω at ${\sigma }_d=0.1$, $u_o=0.12$, $\sigma =0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\rho =0.4$.

4. Analysis of instability

To study the instability of obliquely propagating SWs, we use small-k perturbation expansion method [32, 44] and assume that (27) ${\varphi }_1={\varphi }_o(\mathcal{Z})+\varphi (\mathcal{Z},\zeta ,\eta ,{\tau }^{\setminus }),$(27) where ${\varphi }_o(\mathcal{Z})$ is the soliton solution in Equation (26(26) $\begin{array}{rl}{\varphi }_o(\mathcal{Z})& ={\varphi }_{om}{\mathrm{sech}}^4\kappa \mathcal{Z},\\ {\varphi }_{om}& =\left(\frac{15u_o}{8R_1}\right),\kappa =\frac{1}{4}\sqrt{\frac{u_o}{R_2},}\end{array}$(26) ), and ϕ is given by long wave length plane wave as (28) $\varphi =\phi (\mathcal{Z})e^{i[k({\iota }_{\zeta }\zeta +{\iota }_{\eta }+{\iota }_{\xi }\mathcal{Z})-\omega {\tau }^{\setminus }]},$(28) where $({\iota }_{\zeta },{\iota }_{\eta },{\iota }_{\xi })$ are the direction cosine in which ${\iota }_{\zeta }^2+{\iota }_{\eta }^2+{\iota }_{\xi }^2=1$ . For small, k $\phi (\mathcal{Z})$ and ω could be expanded as (29) $\begin{array}{rl}\phi (\mathcal{Z})& ={\phi }_o(\mathcal{Z})+k{\phi }_1(\mathcal{Z})+k_2^2{\phi }_2(\mathcal{Z}){+}^{\cdots .}\end{array}$(29) (30) $\begin{array}{rl}\omega & =k{\omega }_1+k^2{\omega }_2+\cdots \cdots .\end{array}$(30) By substituting Equation (27(27) ${\varphi }_1={\varphi }_o(\mathcal{Z})+\varphi (\mathcal{Z},\zeta ,\eta ,{\tau }^{\setminus }),$(27) ) in Equation (21(21) $\begin{array}{rl}& \frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }{\tau }^{\setminus }}+R_1\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi }+R_2\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^3}\\ & +R_3\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\zeta }+R_4\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\zeta }^3}\\ & +R_5\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^2\mathrm{\partial }\zeta }+R_6\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\zeta }^2}+R_7\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\eta }^2}\\ & +R_8\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\zeta \mathrm{\partial }{\eta }^2}=0,\end{array}$(21) ), we get the linearized form of Equation (21(21) $\begin{array}{rl}& \frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }{\tau }^{\setminus }}+R_1\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\xi }+R_2\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^3}\\ & +R_3\sqrt{{\varphi }_1}\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }\zeta }+R_4\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\zeta }^3}\\ & +R_5\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }{\xi }^2\mathrm{\partial }\zeta }+R_6\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\zeta }^2}+R_7\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\xi \mathrm{\partial }{\eta }^2}\\ & +R_8\frac{{\mathrm{\partial }}^3{\varphi }_1}{\mathrm{\partial }\zeta \mathrm{\partial }{\eta }^2}=0,\end{array}$(21) ) as (31) $\begin{array}{rl}& \frac{\mathrm{\partial }\varphi }{\mathrm{\partial }{\tau }^{\setminus }}-u_0\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\mathcal{Z}}+R_1\sqrt{{\varphi }_0}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\mathcal{Z}}+\frac{1}{2}{R}_1\frac{\varphi }{\sqrt{{\varphi }_0}}\frac{\mathrm{\partial }{\varphi }_0}{\mathrm{\partial }\mathcal{Z}}\\ & +R_2\frac{{\mathrm{\partial }}^3{\varphi }^{(1)}}{\mathrm{\partial }{\mathcal{Z}}^3}+R_3\sqrt{{\varphi }_0}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\zeta }\\ & +R_4\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }{\zeta }^3}+R_5\frac{{\mathrm{\partial }}^3{\varphi }^{(1)}}{\mathrm{\partial }{\mathcal{Z}}^2\mathrm{\partial }\zeta }+R_6\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\mathcal{Z}\mathrm{\partial }{\zeta }^2}\\ & +R_7\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\mathcal{Z}\mathrm{\partial }{\eta }^2}+R_8\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\zeta \mathrm{\partial }{\eta }^2}=0.\end{array}$(31) Our essential interest is to find ${\omega }_1.$ The zeroth order equation obtained from Equations (28(28) $\varphi =\phi (\mathcal{Z})e^{i[k({\iota }_{\zeta }\zeta +{\iota }_{\eta }+{\iota }_{\xi }\mathcal{Z})-\omega {\tau }^{\setminus }]},$(28) )–(31(31) $\begin{array}{rl}& \frac{\mathrm{\partial }\varphi }{\mathrm{\partial }{\tau }^{\setminus }}-u_0\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\mathcal{Z}}+R_1\sqrt{{\varphi }_0}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\mathcal{Z}}+\frac{1}{2}{R}_1\frac{\varphi }{\sqrt{{\varphi }_0}}\frac{\mathrm{\partial }{\varphi }_0}{\mathrm{\partial }\mathcal{Z}}\\ & +R_2\frac{{\mathrm{\partial }}^3{\varphi }^{(1)}}{\mathrm{\partial }{\mathcal{Z}}^3}+R_3\sqrt{{\varphi }_0}\frac{\mathrm{\partial }\varphi }{\mathrm{\partial }\zeta }\\ & +R_4\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }{\zeta }^3}+R_5\frac{{\mathrm{\partial }}^3{\varphi }^{(1)}}{\mathrm{\partial }{\mathcal{Z}}^2\mathrm{\partial }\zeta }+R_6\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\mathcal{Z}\mathrm{\partial }{\zeta }^2}\\ & +R_7\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\mathcal{Z}\mathrm{\partial }{\eta }^2}+R_8\frac{{\mathrm{\partial }}^3\varphi }{\mathrm{\partial }\zeta \mathrm{\partial }{\eta }^2}=0.\end{array}$(31) ) after integration could be written as (32) $(-u_0+R_1{\varphi }_0){\phi }_o+R_2\frac{d^2{\phi }_o}{\mathrm{d}{\mathcal{Z}}^2}=h,$(32) where h is the constant. Equation (32(32) $(-u_0+R_1{\varphi }_0){\phi }_o+R_2\frac{d^2{\phi }_o}{\mathrm{d}{\mathcal{Z}}^2}=h,$(32) ) is a coupled differential equation in terms of ${\phi }_o$ and ${\varphi }_o$. This equation has the same structure as that of Equation (25(25) $-u_o\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_1\sqrt{{\varphi }_o}\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_2\frac{{\mathrm{\partial }}^3{\varphi }_o}{\mathrm{\partial }{\mathcal{Z}}^3}=0.$(25) ) under the following two solutions: [45] (33) $\begin{array}{rl}f& =\frac{\mathrm{d}{\varphi }_0}{\mathrm{d}\mathcal{Z}},\end{array}$(33) (34) $\begin{array}{rl}g& =f{\int }^{\mathcal{Z}}\frac{\mathrm{d}\mathcal{Z}}{f^2}.\end{array}$(34) The zeroth order solution could be given by (35) ${\phi }_o=h_{1}f+h_{2}g-h{f}_o{\int }^{\mathcal{Z}}\frac{g}{R_2}\mathrm{d}\mathcal{Z}+hg{\int }^z\frac{f_o}{R_2}\mathrm{d}\mathcal{Z},$(35) where $h_1$ and $h_2$ are constants. Integrating Equation (35(35) ${\phi }_o=h_{1}f+h_{2}g-h{f}_o{\int }^{\mathcal{Z}}\frac{g}{R_2}\mathrm{d}\mathcal{Z}+hg{\int }^z\frac{f_o}{R_2}\mathrm{d}\mathcal{Z},$(35) ) under the condition ${\phi }_o$ not tending to $\pm \mathrm{\infty }$ as $\mathcal{Z}$ tends to $\pm \mathrm{\infty }$, ${\phi }_o$ simplified to (36) ${\phi }_o=h_{1}f.$(36) The first-order equation with linear terms in k obtained from Equations (26(26) $\begin{array}{rl}{\varphi }_o(\mathcal{Z})& ={\varphi }_{om}{\mathrm{sech}}^4\kappa \mathcal{Z},\\ {\varphi }_{om}& =\left(\frac{15u_o}{8R_1}\right),\kappa =\frac{1}{4}\sqrt{\frac{u_o}{R_2},}\end{array}$(26) )–(29(29) $\begin{array}{rl}\phi (\mathcal{Z})& ={\phi }_o(\mathcal{Z})+k{\phi }_1(\mathcal{Z})+k_2^2{\phi }_2(\mathcal{Z}){+}^{\cdots .}\end{array}$(29) ) and Equation (34(34) $\begin{array}{rl}g& =f{\int }^{\mathcal{Z}}\frac{\mathrm{d}\mathcal{Z}}{f^2}.\end{array}$(34) ) after integration expressed as (37) $\begin{array}{rl}& (-u_0+R_1\sqrt{{\varphi }_o}){\phi }_1+R_2\frac{d^2{\phi }_1}{\mathrm{d}{\mathcal{Z}}^2}\\ & =i{h}_1({\alpha }_1+\beta {\tanh }^2\kappa \mathcal{Z}){\varphi }_0+C,\end{array}$(37) where C is the integration constant and ${\alpha }_1$ and ${\beta }_1$ are given by (38) $\begin{array}{rl}{\alpha }_1& =({\omega }_1+{\iota }_{\xi }{u}_0-\frac{1}{2}{\varphi }_{0m}{\mu }_1-2{\kappa }^2{\mu }_2),\\ {\beta }_1& =\frac{1}{2}\sqrt{{\varphi }_{om}}{\mu }_1-20{\kappa }^2{\mu }_2,\\ {\mu }_1& =R_1{\iota }_{\xi }+R_2{\iota }_{\zeta },\\ {\mu }_2& =3R_2{\iota }_{\xi }+R_5{\iota }_{\zeta }.\end{array}$(38) Using same steps in calculating ${\phi }_o$ to get the general solution of the first-order equation ${\phi }_1$ as (39) ${\phi }_1=C_{1}f+\frac{i{h}_1}{32R_2^2{\kappa }^2}[({\alpha }_1+{\beta }_1)\mathcal{Z}f+\frac{4}{5}(5{\alpha }_1+{\beta }_1){\phi }_o].$(39) Also, equation for ${\phi }_2$ must be written as (40) $\begin{array}{rl}& (-u_0\frac{\mathrm{d}}{\mathrm{d}\mathcal{Z}}+R_1\frac{\mathrm{d}}{\mathrm{d}\mathcal{Z}}\sqrt{{\varphi }_0}+R_2\frac{{\mathrm{d}}^3}{\mathrm{d}{\mathcal{Z}}^3})\\ & {\phi }_2=i{\omega }_2{\phi }_o+i({\omega }_1+{\iota }_{\xi }{u}_0){\phi }_1,\\ & -i{\mu }_1\sqrt{{\varphi }_0}{\phi }_1+{\mu }_3\frac{\mathrm{d}{\phi }_0}{\mathrm{d}\mathcal{Z}}-i{\mu }_2\frac{{\mathrm{d}}^2}{\mathrm{d}{\mathcal{Z}}^2}{\phi }_1,\end{array}$(40) where (41) ${\mu }_3=3R_2^2{\iota }_{\xi }^2+2R_5{\iota }_{\zeta }{\iota }_{\xi }+R_6{\iota }_{\zeta }^2+R_7{\iota }_{\eta }^2.$(41) Solution of Equation (35(35) ${\phi }_o=h_{1}f+h_{2}g-h{f}_o{\int }^{\mathcal{Z}}\frac{g}{R_2}\mathrm{d}\mathcal{Z}+hg{\int }^z\frac{f_o}{R_2}\mathrm{d}\mathcal{Z},$(35) ) exists when the right hand side in (35(35) ${\phi }_o=h_{1}f+h_{2}g-h{f}_o{\int }^{\mathcal{Z}}\frac{g}{R_2}\mathrm{d}\mathcal{Z}+hg{\int }^z\frac{f_o}{R_2}\mathrm{d}\mathcal{Z},$(35) ) is orthogonal to kernel of operator that adjoint to operator, [45–47] $-u_0\frac{\mathrm{d}}{\mathrm{d}\mathcal{Z}}+R_1\frac{\mathrm{d}}{\mathrm{d}\mathcal{Z}}{\varphi }_0+R_2\frac{{\mathrm{d}}^3}{\mathrm{d}{\mathcal{Z}}^3}.$This kernel tend to zero as $\mathcal{Z}⟶\pm \mathrm{\infty }$. So, one can determining ${\omega }_1$ from (42) $\begin{array}{rl}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\varphi }_0[i{\omega }_2{\phi }_o+i({\omega }_1+{\iota }_{\xi }{u}_0){\phi }_1-i{\mu }_1\sqrt{{\varphi }_0}{\phi }_1\\ & +{\mu }_3\frac{\mathrm{d}{\phi }_0}{\mathrm{d}\mathcal{Z}}+i{\mu }_2\frac{d_1^2{\phi }_1}{\mathrm{d}{\mathcal{Z}}^2}]\mathrm{d}\mathcal{Z}=0.\end{array}$(42) Now using ${\phi }_o$ and ${\phi }_1$ from (36(36) ${\phi }_o=h_{1}f.$(36) ) and (39(39) ${\phi }_1=C_{1}f+\frac{i{h}_1}{32R_2^2{\kappa }^2}[({\alpha }_1+{\beta }_1)\mathcal{Z}f+\frac{4}{5}(5{\alpha }_1+{\beta }_1){\phi }_o].$(39) ), the dispersion relation can obtained as (43) ${\omega }_1={\mathrm{\Omega }}_1-{\iota }_{\xi }{u}_0+({\mathrm{\Omega }}_1^2-\mathrm{{\rm Y}}{)}^{\frac{1}{2}},$(43) where (44) $\begin{array}{rl}{\mathrm{\Omega }}_1& =\frac{16}{21}(\sqrt{{\varphi }_m}{\mu }_1-2{\mu }_2{\kappa }^2),\end{array}$(44) (45) $\begin{array}{rl}\mathrm{{\rm Y}}& =\frac{512}{945}({\varphi }_m{\mu }_1^2-5\sqrt{{\varphi }_m}{\mu }_1{\mu }_2{\kappa }^2-\frac{15}{12}{\mu }_2^2{\kappa }^4\\ & +30R_2{\mu }_3{\kappa }^4\phantom{{\varphi }_m{\mu }_1^2-5\sqrt{{\varphi }_m}{\mu }_1{\mu }_2{\kappa }^2-\frac{15}{12}{\mu }_2^2{\kappa }^4}).\end{array}$(45) It is obvious from dispersion relation (43(43) ${\omega }_1={\mathrm{\Omega }}_1-{\iota }_{\xi }{u}_0+({\mathrm{\Omega }}_1^2-\mathrm{{\rm Y}}{)}^{\frac{1}{2}},$(43) ) that there always instability if $(\mathrm{{\rm Y}}-{\mathrm{\Omega }}^2)$ $>0$. By using Equations (19(19) $\begin{array}{rl}A& =\frac{2}{\frac{2\lambda \mu \rho }{\chi {}^2}+\frac{2}{{\lambda }^3}},\\ B& =-\frac{(\beta -1)\sigma {\mu }_e}{2\sqrt{\pi }},\\ D& =\frac{({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4\mu {\rho }^3}{2{\mathrm{\Omega }}^2\chi {}^2}.\end{array}$(19) ), (22(22) $\begin{array}{rl}{R}_1& =AB\cos \vartheta ,\\ R_2& =\frac{1}{2}A({\cos }^2\vartheta +D{\sin }^2\vartheta \cos \vartheta ),\\ R_3& =-AB\sin \vartheta ,\\ R_4& =-\frac{1}{2}A({\sin }^2\vartheta -D{\cos }^2\vartheta \sin \vartheta ),\\ R_5& =A[D(\sin \vartheta {\cos }^2\vartheta -\frac{1}{2}{\sin }^3\vartheta )\\ & -\frac{3}{2}{\cos }^2\vartheta \sin \vartheta ],\\ R_6& =-A[D({\sin }^2\vartheta \cos \vartheta -\frac{1}{2}{\cos }^3\vartheta )\\ & -\frac{3}{2}\cos \vartheta {\sin }^2\vartheta ],\\ R_7& =\frac{1}{2}AD\cos \vartheta ,\\ R_8& =-\frac{1}{2}AD\sin \vartheta .\end{array}$(22) ), (38(38) $\begin{array}{rl}{\alpha }_1& =({\omega }_1+{\iota }_{\xi }{u}_0-\frac{1}{2}{\varphi }_{0m}{\mu }_1-2{\kappa }^2{\mu }_2),\\ {\beta }_1& =\frac{1}{2}\sqrt{{\varphi }_{om}}{\mu }_1-20{\kappa }^2{\mu }_2,\\ {\mu }_1& =R_1{\iota }_{\xi }+R_2{\iota }_{\zeta },\\ {\mu }_2& =3R_2{\iota }_{\xi }+R_5{\iota }_{\zeta }.\end{array}$(38) ), (43(43) ${\omega }_1={\mathrm{\Omega }}_1-{\iota }_{\xi }{u}_0+({\mathrm{\Omega }}_1^2-\mathrm{{\rm Y}}{)}^{\frac{1}{2}},$(43) ), (44(44) $\begin{array}{rl}{\mathrm{\Omega }}_1& =\frac{16}{21}(\sqrt{{\varphi }_m}{\mu }_1-2{\mu }_2{\kappa }^2),\end{array}$(44) ), and (45(45) $\begin{array}{rl}\mathrm{{\rm Y}}& =\frac{512}{945}({\varphi }_m{\mu }_1^2-5\sqrt{{\varphi }_m}{\mu }_1{\mu }_2{\kappa }^2-\frac{15}{12}{\mu }_2^2{\kappa }^4\\ & +30R_2{\mu }_3{\kappa }^4\phantom{{\varphi }_m{\mu }_1^2-5\sqrt{{\varphi }_m}{\mu }_1{\mu }_2{\kappa }^2-\frac{15}{12}{\mu }_2^2{\kappa }^4}).\end{array}$(45) ), the criteria of instability must be (46) $S_i>0,$(46) where (47) $\begin{array}{rl}{S}_i& ={\iota }_{\eta }^2[-2{\mathrm{\Omega }}^2{\chi }^2-({\lambda }^4\mu {\rho }^3+(1-{\mathrm{\Omega }}^2){\chi }^2){\sin }^2(\vartheta )]\\ & +{\iota }_{\zeta }^2[2{\mathrm{\Omega }}^2{\chi }^2-\frac{9}{7}({\lambda }^4\mu {\rho }^3+({\mathrm{\Omega }}^2-1){\chi }^2){\tan }^2(\vartheta )].\end{array}$(47) Figures 7 and 8 represent $S_i=0$ 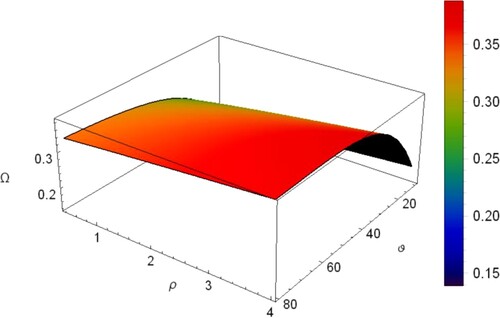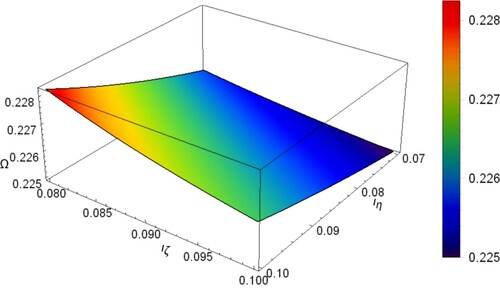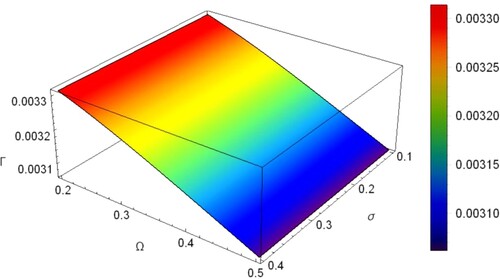surface plot in which the numerical values for the plasma parameters below the surface gives stable wave regime. Where numerical values above the surface plane represent unstable SWs. Figure 7 gives the relation between the dust cyclotron frequency Ω, obliqueness angle ϑ and grain charge ratio ρ. It seems that as ϑ increases the value of Ω associated with the unstable SWs increases. It is also clear from this figure that as ρ increases the value of Ω associated with unstable SWs increases. Figure 8 also represents $S_i=0$ surface plot indicating the variation of Ω with the direction cosine ${\iota }_{\eta }$ and ${\iota }_{\zeta }$. This plot shows that as ${\iota }_{\eta }$ increases the value of Ω associated with unstable SWs increases. On other hand as ${\iota }_{\zeta }$ increases, the value of Ω for which the solitary waves become unstable and decreases. The instability growth rate reads as (48) $\mathrm{\Gamma }=\frac{2u_o\sqrt{((({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4{\mu }_1{\rho }^3)S_i)}}{\begin{array}{c}\sqrt{63}[2{\mathrm{\Omega }}^2\chi {}^2+((-{\mathrm{\Omega }}^2\chi {}^2+\chi {}^2)\\ +{\lambda }^4\mu {\rho }^3{\mathrm{\Omega }}^2){\sin }^2(\vartheta )]\end{array}}.$(48) From Equation (48(48) $\mathrm{\Gamma }=\frac{2u_o\sqrt{((({\mathrm{\Omega }}^2+1)\chi {}^2+{\lambda }^4{\mu }_1{\rho }^3)S_i)}}{\begin{array}{c}\sqrt{63}[2{\mathrm{\Omega }}^2\chi {}^2+((-{\mathrm{\Omega }}^2\chi {}^2+\chi {}^2)\\ +{\lambda }^4\mu {\rho }^3{\mathrm{\Omega }}^2){\sin }^2(\vartheta )]\end{array}}.$(48) ), the growth rate Γ is linear in $u_o$ and nonlinear in Ω, ${\iota }_{\zeta }$, ${\iota }_{\eta }$, 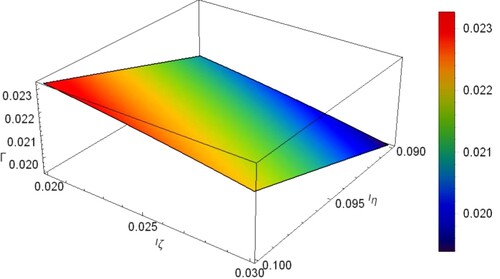ϑ. The instability growth rate Γ variation with ${\iota }_{\eta }$, ${\iota }_{\zeta }$, σ and Ω is shown in Figures 9 and 10. Figure 9 indicates the dependence of Γ on both ${\iota }_{\zeta }$ and ${\iota }_{\eta }$, the unstable perturbation growth rate Γ decreases (increases) with ${\iota }_{\zeta }$ (${\iota }_{\eta }$). 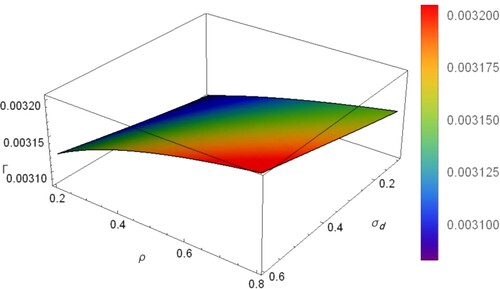From Figure 10, the growth rate decreases slightly with Ω, but σ seems to have no effect on Γ. The grain charge ratio ρ and ${\sigma }_d$ are found to enhance the growth rate as shown in Figure 11.

Figure 7. For $S_i=0$. The variation of Ω with ϑ and ρ for $\sigma =0.1,{\sigma }_d=0.1,\mu =0.1,{\mu }_e=0.3,{\mu }_i=0.5,\delta =20,{\iota }_{\eta }=0.5,{\iota }_{\zeta }=0.4$.

Figure 8. For $S_i=0$. The variation of Ω with ${\iota }_{\zeta }$ and ${\iota }_{\eta }$ for $\sigma =0.1,{\sigma }_d=0.1,\mu =0.1,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta =20,\rho =0.4$.

Figure 9. Variation of Γ with ${\iota }_{\zeta }$ and ${\iota }_{\eta }$ for $u_o=0.12,\mathrm{\Omega }=0.5,\sigma =0.3,{\sigma }_d=0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta =40,\rho =0.4$.

Figure 10. Variation of Γ with Ω and σ for $u_o=0.12,{\sigma }_d=0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta =40,\rho =\mathrm{0.4.}{\iota }_{\eta }=0.09,{\iota }_{\zeta }=0.02$.

Figure 11. Variation of Γ with ρ and ${\sigma }_d$ for $u_o=0.12,\sigma =0.1,\mu =0.7,{\mu }_e=0.3,{\mu }_i=0.5,\vartheta =20,{\iota }_{\eta }=0.09,{\iota }_{\zeta }=0.02$.

5. Conclusion

Four components magnetized dusty plasma formed of mobile positively and negatively dusty particles, electron modelled by vortex-like distribution and Maxwellian ions have been represented. Using the reductive perturbation method, the mZK equation has been deduced. The 3D stability and instability for SWs governed by this mZK equation are examined using the small-k expansion technique. The results could be outlined as

1. As a result of trapped electron distribution, mZK equation has been obtained instead of the standard ZK equation in the case of Maxwellian electron distribution.

2. The soliton solution $\frac{{\varphi }_o}{{\varphi }_{om}}=sec{h}^4(\kappa Z)$ for mZK equation (25(25) $-u_o\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_1\sqrt{{\varphi }_o}\frac{\mathrm{\partial }{\varphi }_o}{\mathrm{\partial }\mathcal{Z}}+R_2\frac{{\mathrm{\partial }}^3{\varphi }_o}{\mathrm{\partial }{\mathcal{Z}}^3}=0.$(25) ) causes DA solitary waves to have smaller width, larger amplitude and higher propagation velocity compared with the solution $\frac{{\varphi }_o}{{\varphi }_{om}}=sec{h}^2(\kappa Z)$ which is considered as a solution for well known ZK equation in the case of assuming Maxwellian electron distribution.

3. This system supports only the propagation of positive potential solitary waves.

4. The temperature ratio $\beta =\frac{T_h}{T_{ht}}$ is found to change the SWs amplitude only. As $|\beta |$ decreases, the amplitude increases. On the other hand, $|\beta |$ has no effect on the width of the SWs.

5. The increase in the grain charge ratio is found to make the amplitude of the SWs higher but cannot change its polarity. On other hand, the solitary wave width increases with $\rho \gtrsim 1.2$ but decreases with $\rho \lesssim 1.2$.

6. The cyclotron frequency Ω seems to have no effect on the SWs amplitude. However, it directly affects the width. It was noted that as Ω increases, the width decreases, i.e. cyclotron frequency Ω makes SWs more spiky.

7. Cyclotron frequency Ω, the temperature ratio ${\sigma }_d$, direction cosine (${\iota }_{\eta }$ and ${\iota }_{\zeta }$) and grain charge ratio ρ are found to modify the instability growth rate Γ of the SWs.Lastly, the current study can provide an explanation for the behaviour of the solitary structure which exists in the four component dusty plasma system with dust opposite polarity, ion Maxwellian distribution and vortex-like electron distribution, which allows us to detect the DA solitary wave and to identify their stability and instability features as it was theoretically predicted in this investigation.

Disclosure statement

No potential conflict of interest was reported by the author(s).