From conventional to inverse magnetocaloric effect in GdMn_1-xCr_xO₃

Abstract

In this work, a phenomenological model (PM) is used to simulate the magnetocaloric effect (MCE) of GdMn_1-xCr_xO₃ (0 ≤x ≤0.4) (GMCO) samples through the modelling of experimental isofield thermo-magnetization curves. The results showed that the MCE of GMCO samples depends strongly on Cr content, achieving a conventional MCE for low Cr content (level of doping x ≤ 0.3). However, the MCE of a higher Cr content sample has an inverse MCE. The behaviour of MCE in GMCO samples indicated that GMCO compounds are interesting magnetocaloric materials and can fruitfully be functioned as cryogenic magnetic refrigerants below 40 K especially in radiation detectors for outer space research.

KEYWORDS:

• Phenomenological model
• magnetocaloric effect
• GdMn_1-xCr_xO₃

1. Introduction

With accelerated steps, the magnetic refrigerator (MR) has become a strong alternative to the gas refrigerator because of its more efficient cooling performance, less weight, more mechanical stability, less damage to the environment, and more energy savings [1–6]. MR is an essential requirement in aerospace applications, medical devices, space applications, and food cooling [7–14]. MR relies on the idea of applying the magnetocaloric effect (MCE) to magnetocaloric (MC) materials in the range of temperatures close to the temperature of the magnetic phase transition $(T_{MPT})$ [15–20]. The MCE is a phenomenon in which magnetic entropy change (ΔS_M) of MC materials occurs when they are subjected to a change in an external magnetic field (H_exe) [21–28]. In order for the development and improvement of MR to happen, the researchers studied different types of magnetic materials such as magnetic alloys, manganites and others [29–36]. In a traditional MCE, the cooling action in MC material happens as a reaction of adiabatic demagnetization process that is performed by a sudden eliminating of H_exe [37]. Quite the reverse, MC materials can be cooled via adiabatic magnetization, which is done by increasing H_exe on diamagnetic materials. This effect is termed an “ inverse MCE” [38]. This inverse MCE appears clearly in antiferromagnetic (AFM) materials over the temperature range of the AFM transition.

There is a strong interest in studying rare earth manganites owing to unusual magnetic ordering such as AFM and spin reorientation as results of unusual spin arrangements [39–41]. Manganites of the RMnO₃ type usually contain undersized trivalent R ions, such as GdMnO₃, and exhibit ferroelectricity caused by magnetic interaction competition, evoking an AFM spin ordering that results in lattice modulations [42]. Tiwari et al. investigated GdMn_1-xCr_xO₃ (GMCO) with 0 ≤x ≤0.4 prepared via sol–gel technique showing well to do sequence of magnetic transitions and recommending that GMCO compounds can be functioned in the fields of magnetic switching, MR and spintronic applications [42]. From this practical point, the MCE of GMCO compounds is studied in this work. In this research, a phenomenological model (PM) is used to study the thermomagnetic properties through the work of simulated magnetization temperature curves for GMCO, concluding magnetic entropy change (ΔS_M), heat capacity change ($\mathrm{\Delta }{C}_{P,H}$), and relative cooling power (RCP).

2. Theoretical considerations

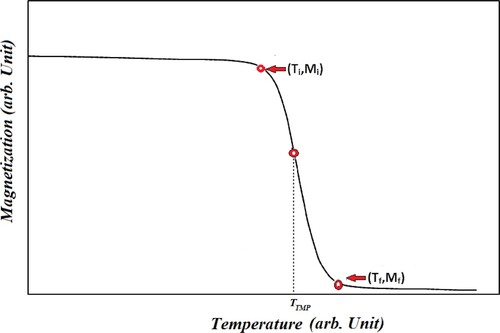
According to PM, described in [43, 44], the dependence of magnetization (M) on temperature (T) is given by: (1) $\begin{array}{rl}M(T)& =\left(\frac{M_i-M_f}{2}\right)\left[\tanh (\alpha (T_{MFT}-T))\right]\\ & +\beta (T-T_{MFT})+\left(\frac{M_i+M_f}{2}\right),\end{array}$(1) where $M_i$ is an initial value of magnetization at a ferromagnetic (FM) or AFM-paramagnetic transition and $M_f$ is a final value of this transition as shown in Figure 1, where $\alpha =\frac{2(\beta -\gamma )}{M_i-M_f}$, $\beta ={\left(\frac{dM}{dT}\right)}_{average}$ for FM or AFM phase, and$\gamma ={\left(\frac{dM}{dT}\right)}_{T=T_{MFT}}$.

Figure 1. The dependence of isofield magnetization vs. temperature.

3. Results and discussion

To simulate the MCE of GMCO, PM parameters for GMCO were determined directly from experimental data (magnetization vs. temperature) as in Ref. [42]. Figure 2 shows the magnetization vs. temperature for GMCO where the experimental data from Ref. [42] are symbolized by symbols, while the simulated data are symbolized by dashed lines. The PM parameters are tabulated in Table 1. We can realize from Figure 2 that there is a satisfied agreement between the experimental and the theoretical ones of M(T) for GMCO samples under 0.05 T, approving PM is a good model for fitting magnetization vs. temperature. The M(T) curves of GMCO samples reveal that GMCO samples are showing a clear second order magnetic transition. $T_{MPT}$ of GMCO samples increases slightly with Cr content. Interestingly, when x is 0.4, a magnetization reversal is observed in GMCO, which expects the existence of an inverse MCE, as we will show later.

Figure 2. Magnetization vs. temperature for GMCO samples in H_exe of 0.05 T. The dashed curves are modelled results and symbols represent experimental data from Ref. 42.

Table 1. The PM parameters for GMCO at H_exe= 0.05 T.

Level of doping (x)	Type of MCE	Mi (emu/g)	Mf (emu/g)	TMPT (K)	$\beta$ (emu/g.K)	$\alpha$ (emu/g.K)
0.1	conventional	20	0.7	11	−0.004	−1.33
0.2	conventional	15.9	0.6	11	−0.006	−0.9
0.3	conventional	2.8	0.6	9.5	−0.012	−0.24
0.4	inverse	−5.8	0.9	16	0.02	0.33
0.4	conventional	1.1	0.3	59.2	0.02	−0.023

$\mathrm{\Delta }{S}_M$ of GMCO samples under adiabatic magnetic field shift (ΔH) of 0.05 T is formulated by. (2) $\begin{array}{rl}\mathrm{\Delta }{S}_M(T,\mathrm{\Delta }H)& =\text{0}\text{.05 }(-\left(\frac{M_i-M_f}{2}\right)\alpha \text{sec}{\text{h}}^{\text{2}}\\ & \times (\alpha (T_{MPT}-T))+\beta \phantom{\left(\frac{M_i-M_f}{2}\right)}).\end{array}$(2)

A maximum of $\mathrm{\Delta }{S}_M$ (ΔS_Max) can be determined when T = T_MPT as follows: (3) $\Delta S_{Max}=0.05\left(-\left(\frac{M_i-M_f}{2}\right)\alpha +\beta \right)$(3)

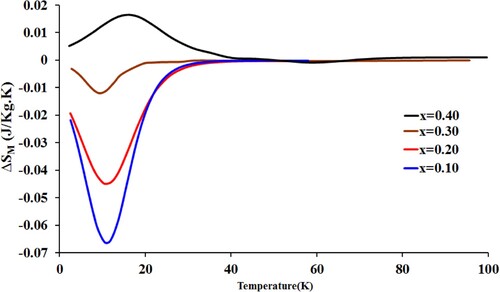
Figure 3 shows the simulated temperature dependence of ΔS_M for GMCO samples under ΔH of 0.05 T, calculated by using Equation (2). Interestingly, $\Delta S_M$ of GMCO depends strongly on Cr content, concluding that the thermomagnetic property of GMCO is characterized as a conventional MCE for low Cr content (level of doping x ≤ 0.3). However, the thermomagnetic property of GMCO is characterized as an inverse MCE when the level of doping x is 0.4 as a result of magnetization reversal below the compensation temperature (T_comp), at which the opposing magnetic moments are equal. But, above T_comp, the thermomagnetic of GMCO characterizes as a conventional MCE with a very small value of $\mathrm{\Delta }{S}_M$ as a result of a FM transition. This magnetization reversal, which causes an inverse MCE below T_comp when the level of doping x is 0.4, is due to negative exchange interaction between Gd and Cr ions. At below T_comp, when H_exe is applied, the spins of Cr³⁺ are directed along the H_exe direction while the spins of Gd³⁺ are directed opposite to that of the H_exe direction. At the same time, the magnetic moment of Gd³⁺ is more than magnetic moment of Cr³⁺ ion. Therefore, the net magnetization of the highly Cr content sample is negative value. However, at above T_comp, when H_exe is applied, magnetic moment of Cr³⁺ is greater than the magnetic moment of Gd³⁺ resulting in a net positive magnetization, causing a conventional MCE.

Figure 3. ΔS_M vs. temperature for GMCO samples in ΔH of 0.05 T.

The effectiveness of GMCO samples as MC material can be evaluated by RCP. This parameter is accounted for by the absolute value of ΔS_Max and full-width at half-maximum ($\delta T_{FWHM}$) of the ΔS_M curve by following the formula: (4) $RCP={|\Delta S(T,H_{max}){|}_M}_{ax}\times \delta T_{FWHM},$(4) where $\delta T_{FWHM}$ can be obtained as follows: (5) $\delta T_{FWHM}=\frac{2}{\alpha }\text{cos}{\text{h}}^{\text{ - 1}}\left(\sqrt{\frac{2\alpha (M_i-M_f)}{\alpha (M_i-M_f)+2\beta }}\right)$(5)

Table 2 indicates that $\delta {\text{T}}_{\text{FWHM}}$ has moderate values and is ranged between 11.3 and 25.5 K for GMCO samples under ΔH of 0.05 T. Furthermore, MC properties decrease dramatically with Cr content.

Table 2. The predicted values of MC properties for GMCO under ΔH of 0.05 T.

Level of doping (x)	TMPT (K)	|ΔSMax| (J/Kg.K)	δTFWHM (K)	RCP (J/Kg)	ΔCP,H(Max) (J/Kg.K)	RC (J/Kg)
0.1	11	0.067	16.7	1.11	0.11	0.79
0.2	11	0.045	19.7	0.89	0.07	0.63
0.3	9.5	0.012	11.3	0.14	0.02	0.10
0.4	16, 59.2	0.017	25.5	0.42	0.01	0.30

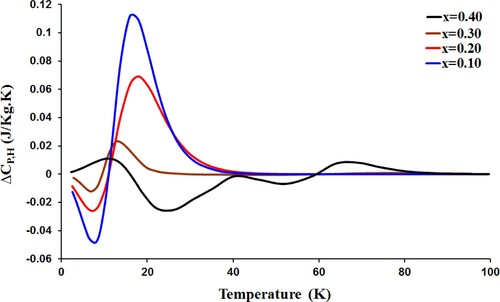
According to the PM model [43], the characterization of $\mathrm{\Delta }{C}_{P,H}$ curves of the GMCO samples can be predicted as follows. (6) $\begin{array}{rl}\mathrm{\Delta }{C}_{P,H}& =-\text{0}\text{.05}{\alpha }^{2}T(M_i-M_f)\tanh (\alpha (T_{MPT}-T))\\ & \times \text{sec}{\text{h}}^{\text{2}}(\alpha (T_{MPT}-T)).\end{array}$(6) Figure 4 shows the temperature dependence of simulated ΔC_P,H for GMCO samples under ΔH of 0.05 T. For low Cr content (level of doping x ≤ 0.3), the simulated $\mathrm{\Delta }{C}_{P,H}$ varies from a negative value to a positive one around$T_{MPT}$, adding a change in the total specific heat. However, the inversed characterization is observed when level of doping x is 0.4 as the result of magnetization reversal below T_comp. But, above T_comp, the simulated $\mathrm{\Delta }{C}_{P,H}$ has the same characterization of lower Cr content samples (level of doping x ≤ 0.3) as a result of the FM transition. The oscillating temperature dependence of $\mathrm{\Delta }{C}_{P,H}$ at temperatures is a reflection of ΔS_M behaviour due to different exchange interactions between Gd and Cr ions below and above 40 K as explained before [42].

Figure 4. ΔC_P,H vs. temperature for GMCO samples in ΔH of 0.05 T.

To investigate further details about MCE in GMCO samples, the refrigerant capacity (RC) is well-thought-out to judge the efficiency of GMCO samples as effective MC materials in MR. RC was calculated as follows [44]: (8) $RC=\underset{T_C-\frac{\delta T_{FWHM}}{2}}{\overset{T_C+\frac{\delta T_{FWHM}}{2}}{\int }}\Delta S_{M}dT.$(8)

Form Table 2, RC decreases with Cr content for a level of doping x ≤ 0.3. However, for further Cr content, RC improves with Cr content. Table 3 gives a comparative image of MCE parameters of GMCO samples with the corresponding ones of several MC materials in same value of ΔH and higher ones in published works. Importantly, the MCE parameters of GMCO samples are higher or as good as the corresponding MCE parameters of these published works with the same value of ΔH or larger. Interestingly, although the of ΔH in the published Gd single crystal is twenty times of the best investigated GMCO sample, |ΔS_Max| of Gd single crystal is larger about 5.5 times. Moreover, GMCO samples are effective MC materials below 40 K due to the sequence of magnetic transitions below this temperature.

Table 3. The values of MC properties for GMCO and other MC materials.

Composition	ΔH (T)	TMPT (K)	|ΔSMax| (J/Kg.K)	δTFWHM (K)	RCP (J/Kg)	ΔCP,H(Max) (J/Kg.K)	Ref.
GMCO	0.05	11-59.2	0.017-0.067	11.3-25.5	0.14-1.11	0.01-0.11	This work
La1-xCdxMnO3	0.05	198–240	0.011	29.65—44.03	0.326— 0.484	0.087—0.105	[46]
Zn0.6Ni0.4Fe2O4	1.7	435.8-559	0.025	–	–	–	[47]
Ni2 + xMn1−xGe	0.05	150–239	0.019—0.02	33	0.63—0.68	0.12—0.21	[48]
(001)-oriented MnAs films	0.03	222–263	0.01-0.02	55.47—75.50	0.07—1.22	0.07-0.083	[49]
Gd1−xCaxBaCo2O5.5	0.1	273–295	1.65E-6—2.2 E-6	9.77—13.85	1.61 E-5 – 3.04 E-5	6.14 E-5  – 6.34E-5	[50]
La1.25Sr0.75MnCoO6	0.5	200–205	0.0175	26—124	0.45, 2.18	0.04-0.19	[51]
BiFe1−xZnxO3	1	628–631	0.005- 0.006	4.9-6.9	0.27-0.40	0.022-0.038	[52]
NdMnO3	1	8–12	3.7 E-3	6.8	0.025	–	[53]
Ge0.95Mn0.05 Films	0.1	85–120	4E-7—3.6 E-6	12.69—17.75	6.3 E-6 – 0.451 E-5	7.7 E-6—1.1 E-4	[54]
BiFe1−xZnxO3	1	629–631	5E-3- 6 E-3	5–7	0.27-0.40	2.2 E-2—3.8 E-2	[55]
Ni58Fe26Ga28	0.2—0.5	263–283	0.005—0.013	42—73	0.19—0.94	0.04—0.07	[56]
Gd single crystal	1	293	0.37	–	–	–	[57]

Finally, GMCO samples are interesting MC materials in cryogenic MR below 40 K especially for devices that function in very low temperatures. For instance, in very low temperature radiation detectors for outer space investigation, where the gravitational effect is non-effective, it is very hard to use ⁴He−³He dilution refrigerators [45]. Therefore, these GMCO compounds are practical MC materials in this situation to overcome the difficulty of working ⁴He−³He dilution refrigerators.

4. Conclusion

The simulation of MCE GMCO compounds containing different Cr content has been done via PM. The results of simulation show that this PM is a constructive model for the calculation of thermomagnetic properties for GMCO compounds. The MCE of GMCO samples depends strongly on Cr content, achieving a conventional MCE for low Cr content (level of doping x ≤ 0.3). However, the MCE of GMCO has a type of inverse MCE when the level of doping x is 0.4 below T_comp. The opportunity to control from conventional MCE to inverse MCE via the level of Cr doping in GMCO increases the prospects for the design of MR. The behaviour of MCE in GMCO samples indicates that they are promising candidates in the cryogenic MR below 40 K.

Disclosure statement

No potential conflict of interest was reported by the author(s).