Slippery boundary and radiative transport in unsteady features of Maxwell fluid over stretched cylinder

Abstract

This article employs the Cattaneo-Christov double diffusion concept to examine thermal and solute energy transfer processes in Maxwell liquid movement. The irregular two-dimensional movement of a Maxwell liquid with changing heat conductivity across an extended cylinder is investigated, together with thermal radioactivity and velocity slip. We develop partial differential equations for heat and mass transmission in Maxwell liquid using the Cattaneo-Christov pattern instead of Fourier's and Fick's law. Numerical shooting solves ordinary differential equations obtained from controlling partial differential equations via similarity transformations. We noticed that unstable factor should be no more than one for optimal outcomes. Greater Maxwell values minimize the movement field and increase liquid energy transfer. Heat and concentration diffusions in Maxwell liquids decline as thermal and concentration relaxation times approach maximum. In addition, a low thermal conductivity characteristic improves the temperature field.

KEYWORDS:

• Thermal radiation
• Cattaneo-Christov pattern
• Maxwell liquid
• variable thermal conductivity
• slip effect

1. Introduction

Heat transmission is vital to the industrial and scientific communities. Microelectronics, fuel cells, heat exchangers, etc. are included. The features of heat transport are studied using Fourier's law [1] (when the temperature gradient is negative, heat movement increases). Various disciplines (advanced surgery and medical treatments) require greater momentum liquidities as well as decreasing time ranges, therefore the system's thermal equilibrium is unattainable because of the short time. Cattaneo [2] thus proposed an improved Fourier's law with a non-vanishing reduction period in the dissipative method. Christov [3] later expanded Cattaneo's pattern. Hayat et al. [4] investigated the Jeffrey liquid movement using the Cattaneo-Christov heat flux pattern. The opposing effect on liquid velocity results from the relaxation to retardation time ratio, according to their findings. Mustafa [5] has also analysed the Maxwell liquid rotational movement by the Cattaneo-Christov heat flux model. Hafeez et al. [6] explored the movement and heat transport of an Oldroyd-B liquid with upper convection over a spinning disc. Nayak et al. [7] analyzed the effect of entropy minimization and nonlinear radioactivity on the electromagnetic movement of nanoliquid via a thin needle's surface.

In the last several decades, nonlinear dynamics of non-Newtonian liquids have been the topic of significant study owing to their intriguing importance in numerous natural phenomena, food processing, medicinal uses, and manufacturing processes. Unlike viscous liquids, the behaviour of non-Newtonian materials seemed to be highly varied and difficult to analyse. Non-Newtonian liquids exhibited fascinating characteristics, such as shear thickening and thinning, liquid memory, die swelling, and yield stress effects. In addition to being classified as nonlinear liquid models, pseudoplastic liquids are also categorized as non-Newtonian liquid models. Williamson liquids are also found in the pseudoplastic type group, which describes the movement behaviour in several human physiological systems. This model's most intriguing characteristic is the steady shift in apparent viscosity between _0 at zero shear rate and as shear rate approaches infinity. There is a range of publications using the Maxwell liquid model in Refs. [8–15].

In the majority of research, the no-slip periphery form (hypothesis that liquids adhere to solids) and $\mathrm{Kn}=0$ (Knudson Number) are established; blends, suspensions, foams, and polymer solutions, on the other hand, don't work well with the no-slip condition [16]. The traditional Navier-Stokes and energy equations may be employed over the scale $0.01<\mathrm{Kn}<0.1$ (slip movement) when velocity slip and temperature leap are accounted for. In recent years, researchers have focused on microscale studies in micro-electro-mechanical systems (MEMS) connected with velocity slip and temperature leap. Sparrow et al. [17] analysed the liquid movement resulting from the revolution of a porous disc using rectilinear slip movement constraints. Torque was significantly reduced due to surface slide. Turkyilmazoglu alog with Senel [18] studied Surface roughness characteristics on heat and mass transmission for a spinning disc with wall suction. Sahoo [19] investigated the influence of partial slip, viscid dissipation, and Joule heating on the movement and temperature transmission of an electrically conducting non-Newtonian liquid caused by a revolving disc. Okechi et al. [20] investigated slip movement in a rough, curved microchannel. Bhatti et al. [21] scrutinized the slip properties on an dense second-order liquid movement in a cylindrical tube with a small diameter.

Thermal radioactivity is used in incineration, nuclear reactors, solar ponds, boiler projects, photovoltaic panels, photo – chemical reactors, turbines, and other technological fields including propelling equipment, satellites, projectiles, spacecraft, etc. Numerous writers have theoretically, experimentally, and statistically investigated the challenges of micropolar liquids that include heat radiation. Mandal and Mukhopadhyay [22] investigated that as the mixed convection constraint grows, heat and angular speed drop, then liquid speed intensifies across an exponentially extended sheet containing an exponentially moving free stream in heat radioactivity. Rashidi et al. [23] employed homotopy assessment to provide approximative analytic results to the nonlinear equations regulating micropolar liquid movement with thermal radioactivity and temperature transfer in a absorbent media. Mahabaleshwar et al. [24] examined the inclined magnetic field as well as the temperature and bulk transport of a hydromagnetic liquid on a distending or contracting sheet with radiation. Rafiq and Abbas [25] investigated the effects of viscous dissipation and heat radioactivity on the peristaltic transfer of a Rabinowitsch liquid pattern via a non-uniformly slanting tube. More investigations are in Refs. [26–45].

In light of the above-mentioned works, this note investigates the temperature and group transmission in Maxwell liquid movement across the distended cylinder with thermal radiation and slip effect in an unstable condition. The Cattaneo–Christov double diffusion model is tried for developing the formulas relating to energy and concentration. Using bvp4c, physical challenges are solved numerically. Visualizations and physical analyses of movement, temperature, and concentrate domains are provided.

2. Mathematical formulation

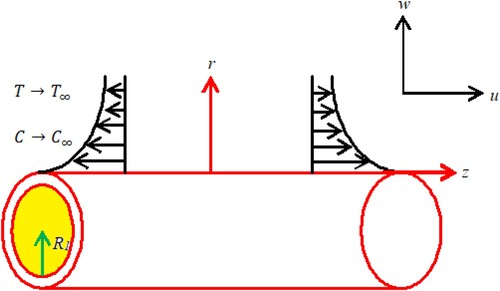
Take into consideration the unstable laminar 2D movement of an incompressible Maxwell liquid across inconstant thermal conductivity in an extended cylinder of radius $R_0$ and slip effect. From illustration 1, assume that u and w are velocity constituents and the $z_0$-axis (the cylinder’s axis) and $r_0$-axis (typical to the $z_0$-axis). The cylinder's time-reliant extending rate is considered as $u_w(t_0,z_0)=\frac{a{z}_0}{1-{\gamma }_1{t}_0}$ where $a,{\gamma }_1>0$. Cattaneo–Christov double diffusion theory transports thermal and solute energy. The Maxwell liquid representation is [8] (1) $\left(1+{\lambda }_1\frac{D}{D{t}_0}\right)S=\mu A_1,$(1) Where ${\lambda }_1$ is the relaxation time, $\frac{D}{D{t}_0}$ indicates the Oldroyd derivative, $S$ the additional stress tensor, $A_1=\mathrm{\nabla }V+(\mathrm{\nabla V}{)}^T$ the first Rivlin–Erickson tensor and $\mu$ the liquid viscosity. If ${\lambda }_1=0$ in Equation (1), the Newtonian liquid pattern is retrieve. In lieu of conventional Fourier's and Fick's laws, the Cattaneo–Christov representation for heat and mass conduction is used. If q and J are heat and mass flows, the ensuing numerical expressions are: [5,7] (2) $\begin{array}{rl}& q+{\lambda }_t\left(\frac{\mathrm{\partial }q}{\mathrm{\partial }{t}_0}+V\cdot \mathrm{\nabla q}+(\mathrm{\nabla V})q-q\cdot \mathrm{\nabla V}\right)=-K(T)\mathrm{\nabla T},\end{array}$(2) (3) $\begin{array}{rl}& J+{\lambda }_c\left(\frac{\mathrm{\partial }J}{\mathrm{\partial }{t}_0}+V\cdot \mathrm{\nabla J}+(\mathrm{\nabla V})J-J\cdot \mathrm{\nabla V}\right)=-D_B\mathrm{\nabla C},\end{array}$(3) where ${\lambda }_t$ denotes the thermal time relaxation; ${\lambda }_c$ the mass time relaxation; $K(T)=k_{\mathrm{\infty }}(1+\mathrm{ϵ\theta })$ the variable thermal conductivity ($k_{\mathrm{\infty }}$ free stream conductivity, $ϵ$ small conductivity factor and $\theta$ the dimensionless temperature); D_B the Brownian difusion coefcient.

If ${\lambda }_t={\lambda }_c=0$ then the two Equations (2) and (3) diminish to conventional Fourier’s and Ficks’s laws, and an incompressible liquid, Equations (2) and (3) turn into (4) $\begin{array}{rl}& q+{\lambda }_t\left(\frac{\mathrm{\partial }q}{\mathrm{\partial }{t}_0}+V\cdot \mathrm{\nabla q}-q\cdot \mathrm{\nabla V}\right)=-K(T)\mathrm{\nabla T},\end{array}$(4) (5) $\begin{array}{rl}& J+{\lambda }_c\left(\frac{\mathrm{\partial }J}{\mathrm{\partial }{t}_0}+V\cdot \mathrm{\nabla J}-J\cdot \mathrm{\nabla V}\right)=-D_B\mathrm{\nabla C},\end{array}$(5)

The fundamental transfer equations for movement, temperature and mass moving of conservation principle (6) $\begin{array}{rl}& \rho \frac{\mathrm{dV}}{d{t}_0}=-\mathrm{\nabla p}+\mathrm{\nabla }\cdot S,\end{array}$(6) (7) $\begin{array}{rl}& (\rho c_p)\frac{\mathrm{dT}}{d{t}_0}=-\mathrm{\nabla }\cdot q,\end{array}$(7) (8) $\begin{array}{rl}& \frac{\mathrm{dC}}{d{t}_0}=-\mathrm{\nabla }\cdot J.\end{array}$(8)

The governing partial differential equations (Figure 1) were constructed by applying mass, momentum, and energy conservation to the complete movement system and deleting S in Equations (1) and (6), q in Equations (2) and (7), and J in Equations (3) and (8): (9) $\begin{array}{rl}& \frac{\mathrm{\partial }(r_{0}u)}{\mathrm{\partial }{z}_0}+\frac{\mathrm{\partial }(r_{0}w)}{\mathrm{\partial }{r}_0}=0,\end{array}$(9) (10) $\begin{array}{rl}& \frac{\mathrm{\partial }u}{\mathrm{\partial }{t}_0}+u\frac{\mathrm{\partial }u}{\mathrm{\partial }{z}_0}+w\frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0}=\upsilon \left[\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{r_0}^2}+\frac{1}{r_0}\frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0}\right]\\ & -{\lambda }_1[\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t_0}^2}+2u\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}_0\mathrm{\partial }{z}_0}+2w\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{r}_0\mathrm{\partial }{t}_0}\\ & +2\mathrm{uw}\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{r}_0\mathrm{\partial }{z}_0}+w^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{r_0}^2}+u^2\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{z_0}^2}],\end{array}$(10) (11) $\begin{array}{rl}& \frac{\mathrm{\partial }T}{\mathrm{\partial }{t}_0}+u\frac{\mathrm{\partial }T}{\mathrm{\partial }{z}_0}+w\frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}\\ & +{\lambda }_t\left[\begin{array}{l}{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{t_0}^2}}+{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{t}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{z}_0}}+2u{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{t}_0\mathrm{\partial }{z}_0}}+{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{t}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}}+2w{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{t}_0\mathrm{\partial }{r}_0}}+2\mathrm{uw}{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{r}_0\mathrm{\partial }{z}_0}}+w^2{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{r_0}^2}}+u^2{\displaystyle \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{z_0}^2}}+u{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{z}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{z}_0}}+w{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{z}_0}}+u{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{z}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}}+w{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{r}_0}}{\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}}\end{array}\right]\\ & =\frac{1}{{(\rho c_p)}_f}\frac{1}{r_0}\frac{\mathrm{\partial }}{\mathrm{\partial }{r}_0}\left[K(T)\left(r_0\frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}\right)\right]+\frac{16\sigma \ast T_{\mathrm{\infty }}^3}{3k\ast {(\rho c_p)}_f}\frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{r_0}^2},\end{array}$(11) (12) $\begin{array}{rl}& \frac{\mathrm{\partial }C}{\mathrm{\partial }{t}_0}+u\frac{\mathrm{\partial }C}{\mathrm{\partial }{z}_0}+w\frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}\\ & +{\lambda }_c\left[\begin{array}{l}{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{t_0}^2}}+{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{t}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{z}_0}}+2u{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{t}_0\mathrm{\partial }{z}_0}}+{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{t}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}}+2w{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{t}_0\mathrm{\partial }{r}_0}}+2\mathrm{uw}{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{r}_0\mathrm{\partial }{z}_0}}+w^2{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{r_0}^2}}+u^2{\displaystyle \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{z_0}^2}}+u{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{z}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{z}_0}}+w{\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{z}_0}}+u{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{z}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}}+w{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }{r}_0}}{\displaystyle \frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}}\end{array}\right]\\ & =D_B\frac{1}{r_0}\frac{\mathrm{\partial }}{\mathrm{\partial }{r}_0}\left[\left(r_0\frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}\right)\right],\end{array}$(12)

Figure 1. Movement structure and organizing scheme.

The periphery conditions that relate to a set of specified issues are as follows [5,7]: (13) $\begin{array}{rl}& u(t_0,z_0,r_0)=u_w(t_0,z_0)+{\gamma }_0\frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0}\\ & =\frac{a{z}_0}{1-{\gamma }_1{t}_0}+{\gamma }_0\frac{\mathrm{\partial }u}{\mathrm{\partial }{r}_0},\text{at}\\ & w(t_0,z_0,r_0)=0,T=T_w,C=C_w\end{array}$(13) (14) $\begin{array}{rl}& u\to 0,T\to T_{\mathrm{\infty }},C\to C_{\mathrm{\infty }}\mathrm{as}{r}_0\to \mathrm{\infty }.\end{array}$(14) where $\upsilon$ denotes the kinematic thickness, $T_w$ and $C_w$ represent heat and absorption near the border, $T_{\mathrm{\infty }}$ and $C_{\mathrm{\infty }}$ the unrestricted movement heat and absorption, $\rho$ the liquid concentration, ${\gamma }_0$ is the slip dimension as a relative coefficient of the slip rate and $c_p$ the definite heat capacity at constant pressure.

Using the subsequent transformation constraints (15) $\begin{array}{rl}& u=-\frac{R_0}{r_0}\sqrt{\frac{\mathrm{a\upsilon }}{1-{\gamma }_1{t}_0}}g(\xi ),w=\frac{a{z}_0}{1-{\gamma }_1{t}_0}{g}^{\mathrm{\prime }}(\xi ),\\ & \theta (\xi )=\frac{T-T_{\mathrm{\infty }}}{T_w-T_{\mathrm{\infty }}},\\ & h(\xi )=\frac{C-C_{\mathrm{\infty }}}{C_w-C_{\mathrm{\infty }}},\xi =\sqrt{\frac{a}{\upsilon (1-{\gamma }_1{t}_0)}}\left(\frac{{r_0}^2-R_0^2}{2R_0}\right).\end{array}$(15)

Equation (9) is fulfilled, and Equations (10)-(14) produce (16) $\begin{array}{rl}& (1+2\mathrm{\alpha \xi })g^{\mathrm{\prime \prime \prime }}+2\mathrm{\alpha g}{g}^{\mathrm{\prime \prime }}-\frac{A}{2}\xi g^{\mathrm{\prime \prime }}-A{g}^{\mathrm{\prime }}-g^{\mathrm{\prime }2}\\ & +g{g}^{\mathrm{\prime \prime }}-\frac{7}{4}{\beta }_1{A}^2\xi g^{\mathrm{\prime \prime }}-\frac{{\beta }_1}{4}{\xi }^2{A}^2{g}^{\mathrm{\prime \prime \prime }}-2{\beta }_1{A}^2{g}^{\mathrm{\prime }}\\ & -2A{\beta }_1{g}^{\mathrm{\prime }2}-{\beta }_1\mathrm{\xi A}{g}^{\mathrm{\prime }}{g}^{\mathrm{\prime \prime }}+A{\beta }_1\mathrm{\xi g}{g}^{\mathrm{\prime \prime \prime }}+3A{\beta }_{1}g{g}^{\mathrm{\prime \prime }}\\ & +2{\beta }_{1}g{g}^{\mathrm{\prime }}{g}^{\mathrm{\prime \prime }}-\frac{\alpha {\beta }_1}{1+2\mathrm{\alpha \xi }}{g}^2{g}^{\mathrm{\prime \prime }}-{\beta }_1{g}^2{g}^{\mathrm{\prime \prime \prime }}=0,\end{array}$(16) (17) $\begin{array}{rl}& (1+2\mathrm{\alpha \xi }){\theta }^{\mathrm{\prime \prime }}\left(1+\frac{4}{3}\mathrm{Rd}\right)+Pr\left(g{\theta }^{\mathrm{\prime }}-\frac{A}{2}\xi {\theta }^{\mathrm{\prime }}\right)\\ & +(1+2\mathrm{\alpha \xi })(\theta {\theta }^{\mathrm{\prime \prime }}+{\theta }^{\mathrm{\prime }2})\epsilon \\ & +2\alpha {\theta }^{\mathrm{\prime }}+2\mathrm{\alpha \epsilon \theta }{\theta }^{\mathrm{\prime }}\\ & -Pr{\beta }_t\left(\begin{array}{l}{\displaystyle \frac{3}{4}}{A}^2\xi {\theta }^{\mathrm{\prime }}-{\displaystyle \frac{3A}{2}}{\theta }^{\mathrm{\prime }}g-{\displaystyle \frac{A}{2}}\xi {\theta }^{\mathrm{\prime }}{g}^{\mathrm{\prime }}{\displaystyle \frac{1}{4}}{A}^2{\xi }^2{\theta }^{\mathrm{\prime \prime }}-\mathrm{A\xi g}{\theta }^{\mathrm{\prime \prime }}+{\theta }^{\mathrm{\prime \prime }}{g}^2+{\theta }^{\mathrm{\prime }}g{g}^{\mathrm{\prime }}\end{array}\right)=0,\end{array}$(17) (18) $\begin{array}{rl}& (1+2\mathrm{\alpha \xi })h^{\mathrm{\prime \prime }}+\mathrm{Le}Pr\left(g{h}^{\mathrm{\prime }}-\frac{A}{2}\xi h^{\mathrm{\prime }}\right)+2\alpha h^{\mathrm{\prime }}\\ & -\mathrm{PrLe}{\beta }_c\left(\begin{array}{l}{\displaystyle \frac{3}{4}}{A}^2\xi h^{\mathrm{\prime }}-{\displaystyle \frac{3A}{2}}{h}^{\mathrm{\prime }}g-{\displaystyle \frac{A}{2}}\xi h^{\mathrm{\prime }}{g}^{\mathrm{\prime }}{\displaystyle \frac{1}{4}}{A}^2{\xi }^2{h}^{\mathrm{\prime \prime }}-\mathrm{A\xi g}{h}^{\mathrm{\prime \prime }}+h^{\mathrm{\prime \prime }}{g}^2+h^{\mathrm{\prime }}g{g}^{\mathrm{\prime }}\end{array}\right)=0,\end{array}$(18) (19) $\begin{array}{rl}& g(0)=0,g^{\mathrm{\prime }}(0)=1+\gamma g^{\mathrm{\prime \prime }}(0),\theta (0)=1,h(0)=1,\end{array}$(19) (20) $\begin{array}{rl}& g^{\mathrm{\prime }}(\mathrm{\infty })=0,\theta (\mathrm{\infty })=0,h(\mathrm{\infty })=0.\end{array}$(20)

In the equations shown above $A\left(=\frac{{\gamma }_1}{a}\right)$ is the instable constraint, $\alpha \left(=\frac{1}{R_0}\sqrt{\frac{\upsilon z_0}{u_w}}\right)$ the curvature constraint, ${\beta }_1\left(=\frac{{\lambda }_1{u}_w}{z_0}\right)$ the Maxwell constraint,$\gamma (={\gamma }_0{(a/\upsilon )}^{1/2})$ the velocity slip constraint, $\mathrm{Pr}\left(=\frac{\upsilon }{{\alpha }_1}\right)$ the Prandtl number, $\mathrm{Rd}\left(=\frac{4{\sigma }^{\ast }{T}_{\mathrm{\infty }}^3}{k^{\ast }k}\right)$ the radioactivity constraint, ${\beta }_t\left(=\frac{{\lambda }_t{z}_0}{u_w}\right)$ the thermal reduction time constraint, ${\beta }_c\left(=\frac{{\lambda }_c{z}_0}{u_w}\right)$ the mass reduction time constraint and $\mathrm{Le}\left(=\frac{{\alpha }_1}{D_B}\right)$ the Lewis number.

Here are the appropriate formulae for the local Nusselt number and the local Sherwood number: (21) $\begin{array}{rl}N{u}_z& =\frac{z_0{q}_w}{k_f(T_w-T_{\mathrm{\infty }})},S{h}_z=\frac{z_0{j}_w}{D_B(C_w-C_{\mathrm{\infty }})},\end{array}$(21) (22) $\begin{array}{rl}{q}_w& =-k_f{\left(\frac{\mathrm{\partial }T}{\mathrm{\partial }{r}_0}+q_r\right)}_{r_0=R_0},j_w=-D_B{\left(\frac{\mathrm{\partial }C}{\mathrm{\partial }{r}_0}\right)}_{r_0=R_0},\end{array}$(22)

Operating dimensionless variables defined in Equation (15) in the above expressions, we get: (23) $\begin{array}{rl}N{u}_{z}R{e}_z^{-1/2}& =-\left(1+\frac{4}{3}\mathrm{Rd}\right){\theta }^{\mathrm{\prime }}(0),\\ S{h}_{z}R{e}_z^{-1/2}& =-h^{\mathrm{\prime }}(0),\end{array}$(23)

Where $R{e}_z=\frac{a{z_0}^2}{\upsilon }$ is the local Reynolds number.

3. Numerical solution

Apparently, the formulated challenge (16-18) with periphery assumptions (19)-(20) cannot be addressed theoretically owing to its considerable nonlinearity. The shooting technique aims to simulate the mathematical solution where the initial periphery value issue is changed into an initial value problem:

The solution to the extremely nonlinear transmuted periphery value issue (16)-(18) is the following system: (24) $\begin{array}{rl}& g=q_1,g^{\mathrm{\prime }}=q_2,g^{\mathrm{\prime \prime }}=q_3,g^{\mathrm{\prime \prime \prime }}={q^{\mathrm{\prime }}}_3,\theta =q_4,\\ & {\theta }^{\mathrm{\prime }}=q_5,{\theta }^{\mathrm{\prime \prime }}={q^{\mathrm{\prime }}}_5,h=q_6,h^{\mathrm{\prime }}=q_7,h^{\mathrm{\prime \prime }}={q^{\mathrm{\prime }}}_7,\end{array}$(24) (25) $\begin{array}{rl}& q_3^{\mathrm{\prime }}=\frac{\begin{array}{l}{q}_2^2-q_1{q}_3+A{q}_2+\frac{A}{2}\xi q_3-2\alpha q_1{q}_3\\ +\frac{7}{3}{\beta }_1{A}^2\xi q_3+2{\beta }_1{A}^2{q}_2+2{\beta }_{1}A{q}_1^2\\ +{\beta }_1\mathrm{\xi A}{q}_1{q}_3-3{\beta }_{1}A{q}_1{q}_3-2{\beta }_1{q}_1{q}_2{q}_3\\ +\frac{\alpha {\beta }_1}{1+2\mathrm{\alpha \xi }}{q}_1^2{q}_3\end{array}}{1+2\mathrm{\alpha \xi }-\frac{{\beta }_1}{4}{\xi }^2{A}^2+A{\beta }_1\xi q_1-{\beta }_1{q}_1^2},\end{array}$(25) (26) $\begin{array}{rl}& q_5^{\mathrm{\prime }}=\frac{\begin{array}{l}Pr{\beta }_t\left(q_1{q}_1{q}_1-\frac{3}{2}A{q}_5{q}_1-\frac{A}{2}\xi q_2{q}_5+\frac{3}{4}{A}^2\xi q_5\right)\\ +Pr\left(\frac{A}{2}\xi q_5-q_1{q}_5\right)-2\alpha q_5\end{array}}{\begin{array}{l}(1+2\mathrm{\alpha \xi })\left(1+\frac{4}{3}\mathrm{Rd}\right)-\frac{Pr}{4}{\beta }_t{A}^2{\xi }^2+{\beta }_{t}APr\xi q_1\\ +(1+2\mathrm{\alpha \xi })\epsilon q_4-Pr{\beta }_t{q}_1^2\end{array}},\end{array}$(26) (27) $\begin{array}{rl}& q_7^{\mathrm{\prime }}=\frac{\begin{array}{l}\mathrm{Le}Pr{\beta }_c(q_1{q}_2{q}_7-\frac{3}{2}A{q}_7{q}_1\\ -\frac{A}{2}\xi q_2{q}_7+\frac{3}{4}{A}^2\xi q_7)\\ +\mathrm{Le}Pr\left(\frac{A}{2}\xi q_7-q_1{q}_7\right)-2\alpha q_7\end{array}}{\begin{array}{l}(1+2\mathrm{\alpha \xi })-\frac{\mathrm{Le}Pr}{4}{\beta }_c{A}^2{\xi }^2+{\beta }_c\mathrm{ALe}Pr\xi q_1\\ -\mathrm{Le}Pr{\beta }_c{q}_1^2\end{array}},\end{array}$(27)

The following are the periphery settings for the first-order differential method described above: (28) $\begin{array}{rl}& q_1(0)=0,q_2(0)=1+\gamma q_3(0),q_4(0)=1,q_6(0)=1,\end{array}$(28) (29) $\begin{array}{rl}& q_2(\mathrm{\infty })=0,q_4(\mathrm{\infty })=0,q_6(\mathrm{\infty })=0.\end{array}$(29)

4. Discussion of results

As opposed to Fourier's and Fick's law, the Cattaneo-Christov temperature and mass flux pattern is used in this study to estimate heat and mass transmission characteristics in the instable movement of Maxwell liquid approaching a extended cylinder. It is notable to mention that ${\beta }_1=0.2,\alpha =0.1,A=0.1,\mathrm{Pr}=6.2,\mathrm{Rd}=0.1,ϵ=0.2,{\beta }_t=0.5,\gamma =0.1,\mathrm{Le}=1.0,{\beta }_c=0.4$ are chosen during the computations. Numerous relevant constraints, including the velocity slip constraint γ, Maxwell liquid constraint ${\beta }_1$, Prandtl number Pr, radiation constraint Rd, thermal conductivity constraint ε and Lewis number Le, are examined for their impacts. $A=0$ corresponds to steady–state movement problem, $A>0$ relates to augmented movement; here, an attracted movement result is attained, whereas $A<0$ indicates decelerated movement. The Cattaneo-Christov heat and mass fluctuation pattern is curtailed to conventional Fourier and Fick law by setting ${\beta }_t=0={\beta }_c$. The range of the prarameters are taken to be $0.0\le A\le 0.8,0.1\le \gamma \le 1.0,0.1\le \alpha \le 0.7,0.1\le {\beta }_1\le 0.5,3.0\le \mathrm{Pr}\le 5.0,0.0\le ϵ\le 0.4,0.0\le {\beta }_t\le 0.4,0.0\le \mathrm{Rd}\le 1.0,0.5\le \mathrm{Le}\le 1.5,0.0\le {\beta }_c\le 0.4$.

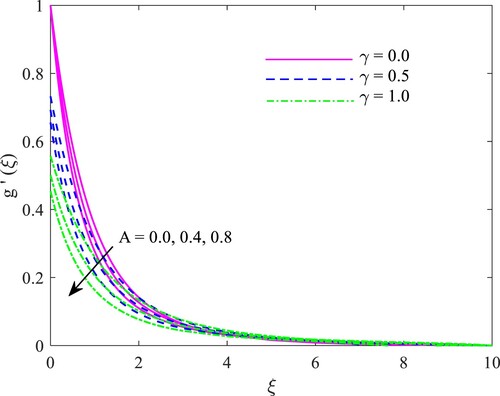
To elucidate the effect of unsteady constraint $A$ and slip constraint $\gamma$ on velocity distribution $g^{\mathrm{\prime }}$, Illustration 2 is sketched. The sketched traces demonstrate that for intensifying values of both constraints, the velocity profile is regarded gradually because the unsteadiness factor results in lower stretching rate, which ultimately drops the velocity profile. Improved velocity displacement reduces the immovable surface's ability to penetrate the periphery sheet. It decreases the viscosity of the momentum periphery sheet as the movement decelerates with increasing slip, and $\gamma =0$ denotes the conventional no-slip condition.

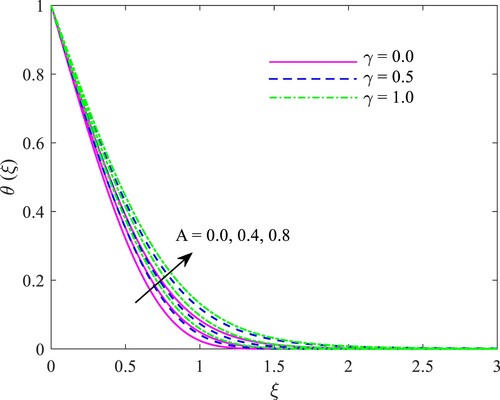
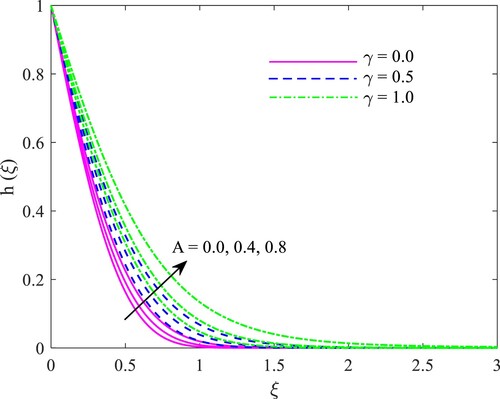
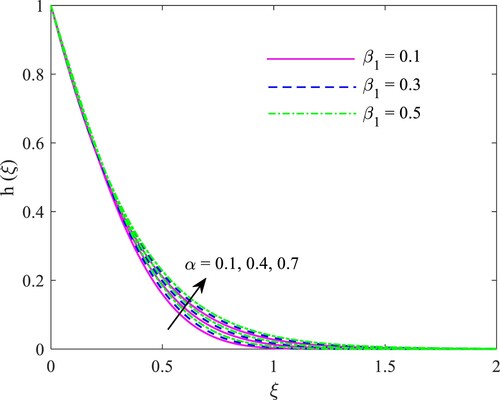
A discussion of the effects of $A$ and $\gamma$ on the heat dispersal is presented in Figure 2. The liquid temperature profile is enhanced with increasing velocity slip values and unsteady constraints. The variation in concentration profile toward unstable and slip constraints can be examined in Illustration 4. It has been noticed that there is a rise in the concentration distribution along with the increasing values of $A$ and $\gamma$.

Figure 2. Variation in $\theta (\xi )$ against the variation in $A$ and $\gamma$.

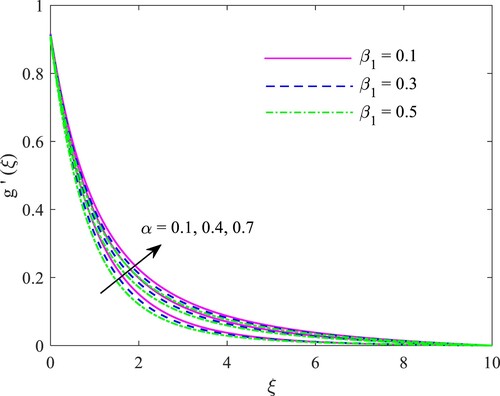
Illustration Figures 5–8 illustrates the influence of curvature and Maxwell constraints on speed, heat, and absorption. For greater values of the curvature constratint $\alpha$, we observed an upward inclination in the domains of speed, heat, and absorption. Substantially, a greater value of $\alpha$ lowers the cylinder’s range; hence, the effect of the periphery on liquid movement is less. The result is liquid rate rises, and the liquid’s heat and mass movement also increase. We noticed- cylinders carry mometum more efficiently than sheets. For rising levels of the Maxwell constraint ${\beta }_1$, the temperature and concentration fields exhibit an upward trend. The Maxwell constraint ${\beta }_1$ characterizes the rheology of materials with viscoelastic properties. The dimensionless relaxation time is the dimensionless Maxwell constraint ${\beta }_1$. Given the material flexibility, relaxation time represents stress relaxation (retained in the a material distortion when stress is applied abruptly). Therefore, substances with a greater value of ${\beta }_1$ behave as solids. It indicates that the material need longer time to keep its deformation. The result is that the liquid velocity drops owing to the increased value of ${\beta }_1$. In contrast, the energy transport phenomenon accelerates the same trend of ${\beta }_1$ owing to a rise in the heat conduction rate.

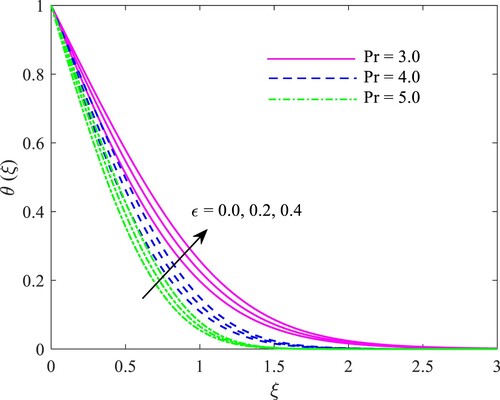
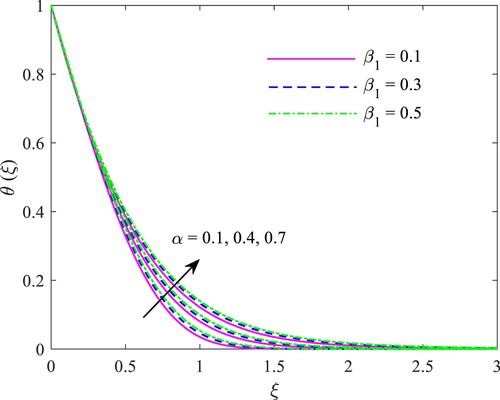
Figure 3 depicts thermal conductivity constraint $ϵ$ and Prandtl number’s $\mathrm{Pr}$ effect on heat circulation. The heat conductivity constraint $ϵ$ increases the liquid's heat transport proportion and the heat field. As a significant liquid’s thermophysical feature, the Prandtl number quantifies the proportion of momentum diffusivity to thermal diffusivity in the domain. For $\mathrm{Pr}<1$, heat diffusivity is greater than momentum diffusivity. In other words, liquids with low viscosity and high conductivity, such as air and other gases, correlate to lesser Prandtl numbers. For $\mathrm{Pr}=1$, the viscous and energy diffusion rates, as well as the thermal and velocity (momentum) periphery level viscosities, will be identical. If $\mathrm{Pr}>1$,, momentum diffusivity is more than heat diffusivity. Furthermore, water and motor oils possess poor heat conductivity; so, their Prandtl numbers are high. Hence, the thermal periphery level viscosity drops with the upsurge in the Prandtl number.

Figure 3. Variation in $\theta (\xi )$ against the variation in $ϵ$ and $\mathrm{Pr}$.

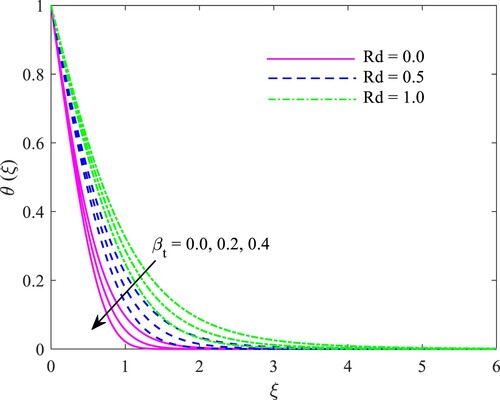
The effects of heat and mass reduction time constraints ${\beta }_t$ and ${\beta }_c$ on the heat and mass transfer rate are shown in Illustrations Figure 9 and Figure 10. As the thermal reduction time and solute reduction time constraints increase, the heat and absorption areas decrease. Larger values of the Cattaneo-Christov reduction time limitation govern the instantaneous propagation of heat waves in a mode. As a consequence of this, a liquid whose relaxation time constraints had rising values required more time to convey heat and mass. The outcome is a decrease in both the heat and absorption areas.

Figure 4 illustrates the radiation constraint Rd’s influence on the temperature field. The radioactivity intensifies the heat as well as the liquid’s thermal periphery level. The heated plate emits heat energy, which will increase the heat and thermal periphery level. Conclusion: the radioactivity is expedient as the prevailing temperature is required. The radiation restriction has no noticeable consequences farther from the boundary.

Figure 4. Variation in $\theta (\xi )$ against the variation in $\mathrm{Rd}$ and ${\beta }_t$.

Illustration Figure 10 depicts the Lewis number $\mathrm{Le}$ outcome on the absorption area. The declined profile of concentration due to $\mathrm{Le}$ is because $\mathrm{Le}$ is directly related to the mass diffusivity, which declined the concentration distribution.

Table 1 provides a comparison of decreased $-f^{\mathrm{\prime \prime }}(0)$ with varied values of ${\beta }_1$, so validating our conclusions. Table 2 shows surface temperature and solute grades for a variety of constraint settings. The Nusselt number attained maximum values for ${\beta }_t,\mathrm{Rd},\alpha$, and minimum values for $A,{\beta }_1,ϵ$. The table depicts that the local Sherwood number attains maximum values for $\alpha ,\mathrm{Le},{\beta }_c$, which converse trend is noted for $A$ and ${\beta }_1$.

Table 1. Numerical values of $-f^{\mathrm{\prime \prime }}(0)$ for different values of ${\beta }_1$ when $\alpha =S=0$.

$-f^{\mathrm{\prime \prime }}(0)$
${\beta }_1$	Abel et al. [9]	Waqas et al. [35]	Present results
0.0	1.000000	1.000000	1.000000
0.2	1.051948	1.051889	1.051812
0.4	1.101850	1.101903	1.101943
0.6	1.150163	1.150137	1.150154
0.8	1.196692	1.196711	1.196723

Table 2. Numerical values of $-\left(1+\frac{3}{4}\mathrm{Rd}\right){\theta }^{\mathrm{\prime }}(0)$ and $-{\varphi }^{\mathrm{\prime }}(0)$ for $\alpha =1$.

$A$	${\beta }_1$	${\beta }_t$	$\epsilon$	$\mathrm{Rd}$	$\alpha$	$\mathrm{Le}$	${\beta }_c$	$N{u}_z$	$S{h}_z$
0.0	0.1	0.1	0.2	0.1	0.1	1.0	0.1	1.646411	1.897996
0.1								1.570411	1.813439
0.2								1.485552	1.721368
0.1	0.2							1.559478	1.803123
	0.3							1.548795	1.793049
	0.4							1.538352	1.783207
	0.1	0.2						1.604997	–
		0.3						1.640100	–
		0.4						1.675656	–
		0.1	0.0					1.760975	–
			0.1					1.658701	–
			0.2					1.570411	–
			0.1	0.0				1.482068	–
				0.2				1.649862	–
				0.4				1.787364	–
				0.1	0.0			1.538882	1.767805
					0.2			1.600003	1.856949
					0.4			1.655419	1.939758
					0.1	2.0		–	2.651212
						3.0		–	3.293016
						4.0		–	3.833736
						1.0	0.2	–	1.967601
							0.3	–	2.112438
							0.4	–	2.249424

5. Final remarks

The analysis, the two-dimensional unstable movement of Maxwell liquid over the extended cylinder, included the use of heat radiation and velocity slip. When seeking to comprehend the mechanistic underpinnings of heat and mass transmission, the Cattaneo-Christov hypothesis is a useful tool. It is a widely held belief that different liquids have different levels of thermal conductivity (temperature reliant). The results are as follows:

1. The slip factors are an effective means of regulating the overall liquid particle velocity throughout the system.

2. The fluctuation in the slip factors results in the surge of the temperature and the concentration of the liquid.

3. The movement field is reduced when the Maxwell constraint ${\beta }_1$ is used, but the heat and absorption allocations increased.

4. Higher values of the heat and mass reduction factors result in a reduction in the amount of heat and mass that may be transported.

5. Both the thermal radiation and heat source constraints increase, elevating the liquid's temperature.

6. The transmitted heat rises as the radiation and curvature constraints that are involved increase (Figures 5–10).

Figure 5. Variation in $g^{\mathrm{\prime }}(\xi )$ against the variation in $A$ and $\gamma$.

Figure 6. Variation in $h(\xi )$ against the variation in $A$ and $\gamma$.

Figure 7. Variation in $g^{\mathrm{\prime }}(\xi )$ against the variation in $\alpha$ and ${\beta }_1$.

Figure 8. Variation in $\theta (\xi )$ against the variation in $\alpha$ and ${\beta }_1$.

Figure 9. Variation in $h(\xi )$ against the variation in $\alpha$ and ${\beta }_1$.

Figure 10. Variation in $h(\xi )$ against the variation in $\mathrm{Le}$ and ${\beta }_c$.

Acknowledgements

The authors are highly obliged and thankful to unanimous reviewers and Editor for their valuable comments on the paper.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.