Characteristics of pressure gradient force errors in a terrain-following coordinate

Abstract

A terrain-following coordinate (σ-coordinate) in which the computational form of pressure gradient force (PGF) is two-term (the so-called classic method) has significant PGF errors near steep terrain. Using the covariant equations of the σ-coordinate to create a one-term PGF (the covariant method) can reduce the PGF errors. This study investigates the factors inducing the PGF errors of these two methods, through geometric analysis and idealized experiments. The geometric analysis first demonstrates that the terrain slope and the vertical pressure gradient can induce the PGF errors of the classic method, and then generalize the effect of the terrain slope to the effect of the slope of each vertical layer (φ). More importantly, a new factor, the direction of PGF (α), is proposed by the geometric analysis, and the effects of φ and α are quantified by tan φ·tan α. When tan φ·tan α is greater than 1/9 or smaller than −10/9, the two terms of PGF of the classic method are of the same order but opposite in sign, and then the PGF errors of the classic method are large. Finally, the effects of three factors on inducing the PGF errors of the classic method are validated by a series of idealized experiments using various terrain types and pressure fields. The experimental results also demonstrate that the PGF errors of the covariant method are affected little by the three factors.

摘要

“地形追随坐标系中气压梯度力误差的特征分析”一文通过几何分析和理想实验，对比了地形追随坐标系两种方案（经典方案和协变方案）中气压梯度力（PGF）误差的特征。结果表明：（1）经典方案的PGF误差受“垂直气压梯度”，“气压梯度的方向（α）”，“垂直层的坡度（φ）”三者影响，垂直气压梯度越大，气压梯度与水平方向的夹角越大，垂直层坡度越大，误差越大；（2）协变方案的PGF误差不受上述三因子影响。此外，通过定义参数TT（TT = tanφ·tanα）能定量分析经典方案的PGF误差。

Keywords:

• Terrain-following coordinate
• pressure gradient force errors
• direction of pressure gradient
• slope of each vertical layer
• nonlinear vertical pressure gradient
• pressure gradient along vertical layer

关键词:

• 地形追随坐标系
• 气压梯度力误差
• 垂直气压梯度
• 气压梯度方向
• 垂直层坡度

1. Introduction

Since a terrain-following coordinate (σ-coordinate) (Phillips 1957) can transform the complex surface of Earth into a regular coordinate surface, the σ-coordinate becomes a common choice for atmospheric and oceanic models. However, the computational form of pressure gradient force (PGF) in a σ-coordinate is two-term (the so-called classic method). These two terms are opposite in sign and of the same order near steep terrain, which induces significant numerical errors; namely, the PGF errors of the σ-coordinate (Haney 1991; Li, Wang, and Wang 2012; Lin 1997; Ly and Jiang 1999; Shchepetkin and McWilliams 2003; Smagorinsky et al. 1967).

Many methods have been proposed to reduce the PGF errors, which can be categorized into three types. The first type is to reduce the PGF errors based on the two-term PGF, and includes high-order schemes (Blumberg and Mellor 1987; Corby, Gilchrist, and Newson 1972; Mahrer 1984; Qian and Zhou 1994), standard stratification deduction (Zeng 1979), and so on. The second type is to overcome the PGF errors through various coordinate transformations based on the non-orthogonal σ-coordinate (Li, Wang, and Wang 2012; Qian and Zhong 1986; Smagorinsky et al. 1967; Yan and Qian 1981; Yoshio 1968). And the third type is to design an orthogonal terrain-following coordinate to bypass the PGF errors (Li et al. 2014). Both methods proposed by Li, Wang, and Wang (2012) and Li et al. (2014) create a one-term computational form of PGF, while Li, Wang, and Wang (2012) proposed to use the covariant scalar equations of the σ-coordinate (the covariant method). Note that studies on the factors inducing the PGF errors are less common than efforts made to reduce the PGF errors.

For the classic method, there are two factors inducing the PGF errors; namely, the terrain slope and the nonlinear vertical pressure gradient (Yan and Qian 1981; Zeng and Ren 1995). Recently, Klemp (2011) proposed that the PGF errors could be minimized when the vertical pressure gradient is nearly linear. The idealized experiments implemented by Li, Li, and Wang (2015) demonstrated that the PGF errors increased according to the increasing terrain slope. However, for the covariant method, few analyses of the factors inducing the PGF errors have been carried out.

In this study, we further explore the factors inducing the PGF errors of the classic and covariant method. In Section 2 we use geometric analysis to identify all the possible factors inducing the PGF errors of the classic method. In Section 3 we implement a series of idealized experiments of various terrain types and pressure fields to investigate the effects of all the factors identified in Section 2 that induce the PGF errors of the classic and covariant method.

2. Geometric analysis of the PGF errors of the classic method

The two-term expression of PGF of the classic method is given by(1)

We abbreviate the first and second term on the RHS of Equation (1(1) ) as PGF1 and PGF2, respectively. According to Equation (1(1) ), the PGF of the classic method is relevant to three factors:

(1)	The pressure gradient along each vertical layer ;
(2)	The vertical pressure gradient ;
(3)	The slope of each vertical layer .

Since the terrain slope equals the slope of the bottom vertical layer in a model, the effect of terrain slope can be included in the effect of each vertical layer on inducing the PGF errors. The effect of the vertical pressure gradient on inducing the PGF errors has been analyzed by many researchers (e.g. Zeng and Ren 1995). Therefore, we only investigate the effects of the pressure gradient along each vertical layer and slope of each vertical layer.

Geometric schematics representing the PGF and its components of different coordinates are illustrated in Figures 1(b)–(d). The AC represents ∇p, AD is the , and CD is the vertical pressure gradient:(2)

Figure 1. Schematic diagrams of PGF vectors and their components of different coordinates.

Notes: Green curves represent a certain vertical layer; blue lines are its tangent and normal directions. S₁, S₂, and S₃ in (a) indicate the areas of different directions of PGF. Panels (b–d) are schematic diagrams of PGF in S₁, S₂, and S₃, respectively. Red lines with solid arrows (AC) represents ∇p. Black- and red-arrowed lines are the components of the PGF of the σ- and z-coordinate, respectively.

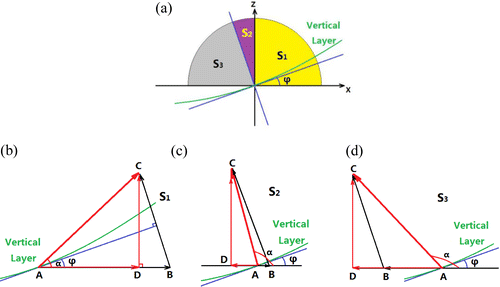
The pressure gradient along each vertical layer is AB:(3)

the direction of PGF (α) is , and the slope of each vertical layer (φ) is given by(4)

In addition, according to the geometric relationship in Figures 1(b)–(d), we obtain(5)

and(6)

Equation (6(6) ) manifests that the pressure gradient along each vertical layer (AB) can be represented by the vertical pressure gradient (CD), the direction of PGF (α) and the slope of each vertical layer (φ). Therefore, the possible factors inducing the PGF errors of the classic method are as follows: (1) the direction of PGF (α); (2) the slope of each vertical layer (φ); (3) the vertical pressure gradient (CD).

According to the different directions, , of PGF (α) in Figure 1(a), we define three situations: (1) S₁: , the yellow area; (2) S₂: , the purple area; (3) S₃: , the grey area. The corresponding schematics of PGF and its components of different coordinates in S₁, S₂, and S₃ are shown in Figures 1(b)–(d), respectively.

The direction of PGF (α) in S₁ is given by(7)

while both of them in S₂ and S₃ are given as follows:(8)

Substituting Equations (2(2) ), (3(3) ), (5(5) ), and (7(7) )/(8) into Equation (1(1) ), we obtain the expression of PGF in S₁, S₂, and S₃, respectively:(9) (10) (11)

According to Equation (11(11) ), the expression of PGF in S₃ is a summation of AB and BD; namely, the PGF errors are consistently small regardless of the terrain slope. Therefore, we only investigate the PGF errors in S₁ and S₂ in the following calculation.

First, using Equations (5(5) ) and (6(6) ), we calculate the proportion between the PGF2 and PGF1 in S₁ (BD and AB in Equation (9(9) )) as follows:(12)

Equation (12(12) ) manifests that . Furthermore, if , the BD and AB are of the same order: namely, the PGF errors are large; otherwise, they are small. Moreover, we abbreviate tan φ·tan α in Equation (12(12) ) as TT, and define a critical value of TT (TT_c) for inducing the PGF errors as follows: if TT > TT_c (0 < TT < TT_c), the PGF1 and PGF2 in Equation (1(1) ) are (are not) of the same order. Substituting Equation (12(12) ) into , we obtain(13)

The 1/9 on the RHS of Equation (13(13) ) is the TT_c in S₁.

Second, using Equations (5(5) ) and (6(6) ), we calculate the proportion between PGF2 and PGF1 in S₂ (AB and BD in Equation (10(10) )) as follows:(14)

Substituting Equation (14(14) ) into , we obtain(15)

The −10/9 on the RHS of Equation (15(15) ) is the TT_c in S₂. The expressions of PGF in S₁, S₂, and S₃, and TT_c in both S₁ and S₂, are all summarized in Table 1.

Table 1. Expressions of PGF, TT, and PGF errors of the classic method in three situations of different directions of PGF.

Situation	Expression of PGF	Critical Condition of TT	PGF1 and PGF2		PGF errors
			Sign	Order
1	AB − BD		Opposite	Same	Large
			Opposite	Different	Small
2	BD − AB		Opposite	Same	Large
			Opposite	Different	Small
3	AB + BD	–	Same	–	Small
		–	Same	–	Small

In addition, when the slope of the vertical layer (φ) or direction of PGF (α) is close to the vertical direction , the absolute value of TT increases. According to Equations (12(12) ) and (14(14) ), the ratio of tends to be a constant one with increasing (decreasing) TT; namely BD is close to AB. Consequently, the difference between the order of AB (BD) and that of AB − BD in S₁ or BD − AB in S₂ is large, and then the PGF errors are large too. Note that, in reality, typhoons, squall lines, and topographic blocking near steep terrain, in which the direction of PGF may be close to the vertical direction, may create large TT, therefore also inducing large PGF errors.

In conclusion, there are three factors inducing the PGF errors of the classic method: (1) the direction of PGF (α); (2) the slope of each vertical layer (φ); (3) the vertical pressure gradient. The effects of α and φ can be quantified by tan φ·tan α (Table 1). Specifically, when or , the PGF errors of the classic method are large; and the closer α or φ is to the vertical direction, the larger the PGF errors of the classic method are.

3. Idealized experiments

In order to investigate the effects of the three factors obtained in Section 2 on inducing the PGF errors of the classic and covariant method, idealized experiments using various terrain types and pressure fields are performed. For consistency, we use the same parameters as Li, Wang, and Wang (2012), except for the terrain and pressure fields. The basic parameters of all the experiments are introduced in Section 3.1. The experiments investigating the effects of the slope of each vertical layer and the direction of PGF are illustrated in Section 3.2. The experiments analyzing the effect of the vertical pressure gradient are demonstrated in Section 3.3.

3.1. Basic parameters

We use the central spatial discretization in the horizontal direction, and the forward scheme in the vertical direction, for the PGF of both methods. The expressions are given as follows:(16) (17)

A 2D bell-shaped terrain type,(18)

is used (Figure 2), where H is the maximum height, a = 5 km is the half width, and h₀ = 50 km is the middle point of the terrain. We use two types of idealized pressure fields, defined as follows (Figure 2): (i) a pressure field with a linear vertical pressure gradient (LP),(19)

Figure 2. Pressure fields given by Equations (19(19) ) and (20(20) ).

Notes: The pressure scale (color bar at the bottom) is in hPa. The black curve in each panel indicates the terrain.

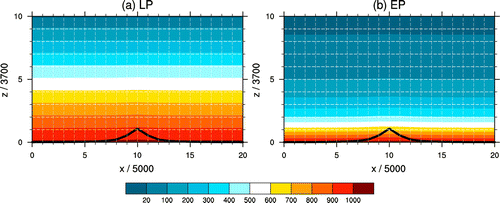
and (ii) a pressure field with an exponential vertical pressure gradient (EP),(20)

where h(x) is the terrain, H is the maximum height of the terrain, p₀ = 1015.0 hPa is the surface pressure, p_t = 10.0 hPa is the top pressure, λ = 8 km is the typical height of the atmosphere, H_t is the top of the domain, and H_p is a parameter to adjust the direction of PGF. The definition of the σ-coordinate, , proposed by Gal-Chen and Somerville (1975), is used. The domain of all the experiments is 0–100 km in the horizontal direction and 0–37 km in the vertical direction. The horizontal and vertical resolutions are 0.5 and 3.7 km, respectively.

3.2. Effects of the direction of the PGF and slope of each vertical layer

We set H in Equation (18(18) ) from 10 to 20 km at 1-km intervals to create steep terrain, and also increase the slope of each vertical layer; and set H_p in Equation (20(20) ) from 0.5H to 1.5H km at 0.1-km intervals to obtain pressure fields with different directions of PGF.

First, we calculate the average TT of every grid in each experiment, and then obtain the TT_c in each experiment. The maximum and minimum TT_c in all the experiments are −0.995 and −1.340, respectively, which are both around its analytical value, , obtained in Section 2, and the average value is −1.116. Moreover, whatever the terrain slope, the minimum and maximum relative errors (REs) of the PGF of the classic method are approximately 0.187 and 0.437, respectively. These results validate that not only the terrain slope (included by the slope of each vertical layer), but also the direction of PGF, needs to be considered in terms of inducing the PGF errors of the classic method, and both effects can be quantified by TT.

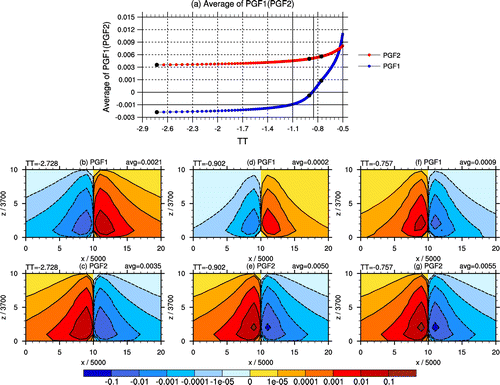
Second, we use the experiments of H = 14 km (TT_c = −1.121, closest to −10/9) as an example to further illustrate the effect of TT_c. Figure 3(a) shows the variation of the average values of PGF1 and PGF2 in different TT. Specifically, when TT < TT_c, the PGF1 and PGF2 are consistently of the same order and opposite in sign (blue and red dotted lines in Figure 3(a), and their patterns at TT = −2.728 are shown in Figures 3(b) and (c) as an example of TT < TT_c. When TT_c < TT < −0.857, the PGF1 and PGF2 are still opposite in sign but no longer of the same order (e.g. the PGF1 and PGF2 at TT = −0.902 shown in Figures 3(d) and (e)). When TT > −0.857 (H_p> H, α is in S₃ of Figure 1(a)), the PGF1 and PGF2 become the same in sign (e.g. the PGF1 and PGF 2 at TT = −0.757 shown in Figures 3(f) and (g)). These results verify the effects of TT_c in S₂ and S₃ of Table 1.

Figure 3. Average of PGF1 and PGF2 at different TT: (a) The variation of PGF1 and PGF2 according to different TT; (b–g) The PGF1 and PGF2 at TT = −2.728, −0.902, and −0.757, respectively.

Note: Black dots in (a) represent the TT of the experiments shown in (b–g).

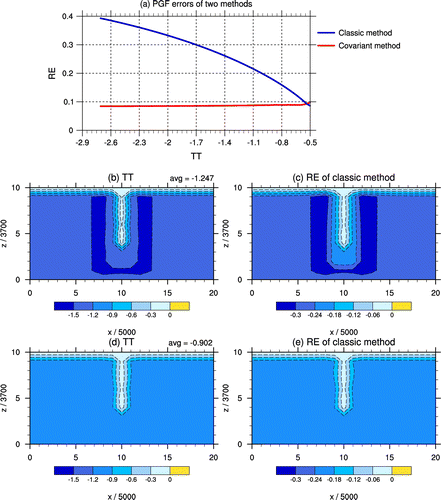
Finally, we also use the results obtained by the experiments of H = 14 km as an example to analyze the variation of the PGF errors of the classic and covariant method according to the increasing TT (Figure 4). The pattern of TT is consistent with that of the REs of the classic method (Figures 4(b) and (c) with TT = −1.247, and Figures 4(d) and (e) with TT = −0.902). Further, the REs of the classic method increase according to the increasing (blue line in Figure 4(a)); however, the REs of the covariant method remain almost the same (red line in Figure 4(a)). These results validate that the PGF errors of the classic method increase according to the increasing TT; whereas, the PGF errors of the covariant method are affected little by it.

Figure 4. REs of the PGF of the classic and covariant method: (a) The variation of REs of the two methods according to different TT; (b, c) The patterns of TT and RE of the classic method when the average TT is −1.247, respectively; (d, e) The patterns of TT and RE of the classic method when the average TT is −0.902, respectively.

3.3. Effects of vertical pressure gradient

We implement two sets of experiments to calculate the PGF of the classic and covariant method using LP and EP. Also, we set H = 4 km in Equation (18(18) ) and H_p = 0.3 km in Equations (19(19) ) and (20(20) ) to consistently compare with the results of the experiments implemented by Li, Wang, and Wang (2012).

The REs of the PGF of both methods are summarized in Table 2. The REs of the classic method in EP are more than twice those in LP; however, the REs of the covariant method are approximately the same in EP and LP. This reveals that the exponential vertical pressure gradient is a factor inducing the PGF errors of the classic method, but not for the covariant method.

Table 2. PGF errors of the classic and covariant methods in LP and EP.

Method	PGF errors
	LP	EP^a
Classic method	1.484	3.336
Covariant method	0.117	0.113

^a Differences between the PGF errors in EP listed here and those in Li, Wang, and Wang (2012) are due to the revised boundary condition.

In conclusion, the three factors inducing the PGF errors of the classic method obtained by the geometric analysis in Section 2 are all validated by the idealized experiments; whereas, none of them has the effect of inducing the PGF errors of the covariant method.

4. Conclusion and discussion

This study investigates the factors inducing the PGF errors of the classic and covariant method through geometric analysis and idealized experiments. Three factors are found that induce the PGF errors of the classic method, including the direction of PGF (α), the slope of each vertical layer (φ), and the vertical pressure gradient; however, none of them induces the PGF errors of the covariant method. Moreover, the effects of α and φ can be quantified by tan φ·tan α (Table 1).

The geometric analysis first demonstrates that the terrain slope and the vertical pressure gradient can induce the PGF errors of the classic method. Then, the effect of terrain slope is generalized into the effect of the slope of each vertical layer (φ). More importantly, a new factor, the direction of PGF (α), is proposed. When or , the two terms of PGF of the classic method are of the same order and opposite in sign. Subsequently, the PGF errors of the classic method are large (Table 1), and the closer the α or φ is to the vertical direction, the larger the PGF errors of the classic method are.

The effects of all of the three factors on inducing the PGF errors of the classic method are validated by a series of idealized experiments. Results first verify the analytical value of TT_c , proposed by the geometric analysis, as well as its effect on inducing the PGF errors of the classic method (Figure 3). It is then found that the PGF errors of the classic method increase according to increasing , and their patterns are also consistent (Figure 4). Finally, results using LP and EP validate that EP can significantly increase the PGF errors of the classic method (Table 2). Moreover, all the idealized experiments demonstrate that the PGF errors of the covariant method are affected little by the three factors. Note that the comparison of the factors inducing the PGF errors of the classic and covariant methods in this study only considers the PGF term; the true benefit of the covariant method needs to be investigated using the equations of the classic and covariant methods in their entirety.

In addition, the difference between the analytical TT_c and the TT_c obtained in the idealized experiments may be due to using the average TT of all the grids. Further analyses need to be carried out to use the average TT of selected grids, in which PGF1 and PGF2 are of the same order. Besides, the three factors tested by the idealized pressure fields in this study are simultaneously changed due to the analytical expression of pressure, Equation (20(20) ). And, only the effects of TT_c in S₂ and S₃ can be tested by this kind of pressure field. Sensitivity experiments using a discrete pressure field, in which each factor can be independently changed, are needed to further investigate the effects of these three factors. Furthermore, experiments using the real pressure field are needed to verify the effect of TT_c.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes on contributor

LI Jin-Xi is a PhD candidate at LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences. His main research interests focus on dynamical core of atmospheric models. Recent publications include papers in Geoscientific Model Development, Atmospheric Science Letters, and Chinese Science Bulletin.

Funding

This work was jointly supported by the National Basic Research Program of China [973 Program, grant number 2015CB954102]; National Natural Science Foundation of China [grant numbers 41305095 and 41175064].