Inverse problem in a porous medium: estimation of effective thermal properties

Abstract

A numerical inverse analysis is presented to simultaneously estimate the effective thermal conductivity, the effective volumetric heat capacity as well as the heat transfer coefficient between a porous medium and a hot wire. The direct problem simulates numerically the hot wire technique considering a porous medium sample. The measured temperature data are generated by adding random errors to the simulated temperatures. An iterative procedure, based on minimizing a sum of squares function with the Levenberg–Marquardt method, is used to solve the inverse problem.

Keywords:

• Effective thermal conductivity
• Inverse analysis
• Hot wire technique
• Porous medium

1. Introduction

The knowledge of the thermal properties of porous media is important for thermal design and numerical simulation. In the past decade, many methods have been presented to determine these properties. Some published works are related to the experimental as well as the theoretical determination of the thermophysical properties, such as the thermal conductivity [1–4] and the heat capacity [5].

The development of the inverse heat transfer problem (IHTP) has progressed more rapidly with the help of a combination of the advent of high technologies, new mathematical achievements and modern computational facilities. Unlike the conventional techniques, the resolution of the IHTP permits the determination of more than one thermophysical property and the apprehension of complex materials. Different techniques (Conjugate Gradient Method [6,7] and Levenberg–Marquardt Method [1,6,8–10]) were performed in the literature and have been used to estimate the thermophysical properties [4–5].

Sawaf et al. [5] presents an inverse analysis to estimate a linearly temperature-dependent thermal conductivity and heat capacity of an orthotropic solid by using simulated transient temperature taken at three locations on the solid's surface. The Levenberg–Marquardt iterative procedure was used to solve the inverse problem.

Huang and Yeh [11] have used the Conjugate Gradient Method to solve the inverse problem in estimating the temperature-dependent thermal conductivity of the homogeneous and non-homogeneous solid material. They used 12 temperatures measured at different positions.

Yang [4] proposed estimating the temperature-dependent thermal conductivity and heat capacity simultaneously from two temperature responses measured at the boundaries of the system.

To our knowledge, the property of the above studies considers solid materials and uses more than two temperatures. On the other hand, there are few studies that estimate the thermophysical properties of unconsolidated materials.

In this article, we propose to determine the thermal parameters of a porous medium using the hot wire method. This method, which is generally used to measure the effective thermal conductivity of unconsolidated media [2,3,12,13], consists of applying a constant heat flux, with a known duration, by using a wire placed in the granular medium. Classically, the measurement of the wire temperature evolution versus time permits us to deduce only the medium effective thermal conductivity using an identification method based on the Blackwell analytic solution [12]. In our study, the IHTP, with only one temperature measurement, is solved to determine three parameters. We first simulate numerically the working of the hot wire method (direct problem). The established model was used, in the experiment design, to determine the optimal position of the temperature sensor, which permits the simultaneous estimation of the effective thermal conductivity, the effective volumetric heat capacity of the porous medium and the heat transfer coefficient between the wire and the medium. The estimation is based on minimizing the least squares function using the Levenberg–Marquardt iterative procedure (inverse problem).

2. Direct problem

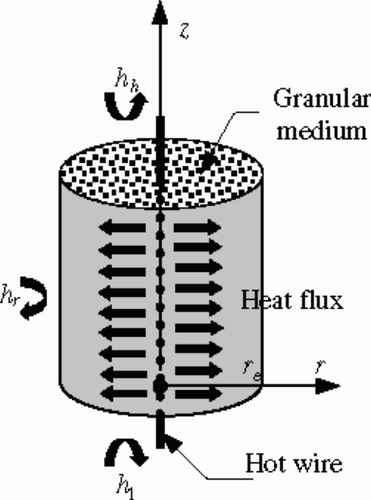
The physical device, considered in this article, is cylindrical. It exchanges heat through lateral and bases areas. The cylinder is filled with an air-saturated porous medium and heated along its axis with a uniform heat flux, given by the wire (figure 1).

Figure 1. The hot wire technique.

The heat transfer in the cylinder is assumed to be two-dimensional. The porous medium is considered homogeneous, isotropic and in local thermal equilibrium.

To bring a certain generality to the results, the analysis is made in terms of dimensionless parameters. So, the dimensionless governing equations are carried out considering the following definitions: (---581--1) where ri and ro are the radius of the hot wire and the cylinder, respectively, (ρCp)f is the fluid volumetric heat capacity, Q is the reference heat flux density, and λe is the effective thermal conductivity.

The dimensionless variables are: (---581--2) where T0 is the ambient and initial temperature.

2.1. Energy equation

When the heat transfer is two-dimensional and depending on the r- and z-axis, the resulting energy equations in terms of the dimensionless variables are as follows: (---581--3) where Ka is the medium volumetric specific heat ratio, Ka = (ρCp)e/(ρCp)f ((ρCp)e = ε(ρCp)f + (1 − ε)(ρCp)s is the medium effective volumetric heat capacity) and γ is the dimensionless wire radius, γ = ri/D.

2.2. Initial and boundary thermal conditions

Initially, we suppose that the temperature in both the cylinder and the wire is constant: (---581--4) where θi is the dimensionless temperature of the wire, assumed to be independent of r.

The heat flux continuity through the lateral surface and bases’ surfaces (R = 1, Z = 0 and Z = A) allows us to write the following equations: (---581--5-) (---581--5-) (---581--5-) where A = H/D is the cylinder aspect ratio and Bix is the Biot number, corresponding to x area (x = r, 1, h respectively for lateral area, base area at Z = 0 and base area at Z = A), defined as: (---581--6) hx is the heat transfer coefficient between the porous medium and the environment around the cylinder through the x area.

The wire is heated by a constant heat flux. Thus, the thermal boundary condition is given by the following expressions: (---581--7) (---581--8) where χ = (1/2)Ksγ, Ks is the volumetric specific heat capacity ratio, Ks = (ρC)i/(ρCp)f, Bii = hiD/λe, the Biot number characterising the heat exchange between the wire and the porous medium and hi is the heat transfer coefficient between the wire and the medium.

The system of the presented equations is solved numerically by the finite volume method as described by Patankar [14]. The advantage of this method is to ensure the flux conservation and thus to avoid the generation of parasitic sources. A regular mesh within the integrated domain was used. The total number of the grid was 81 × 41.

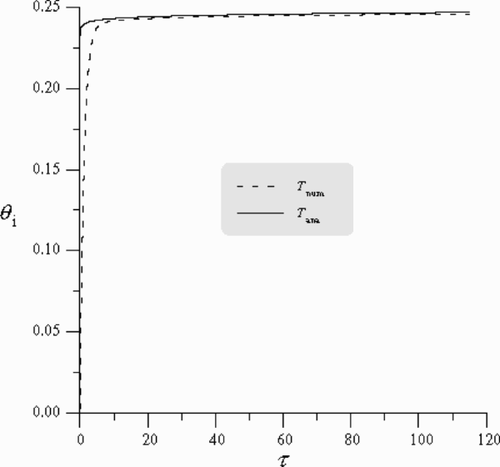
To examine the validity of our numerical results, a comparison was made with the analytical solution developed by Blackwell when the natural convection, radiation heat transfer and two-dimensional effects are negligible.

The Blackwell solution can be expressed, in dimensionless form, as: (---581--9)

For large time, (τ → ∞), this solution becomes: (---581--10) where (---581---1)

Figure 2 shows the wire temperature evolution of the numerical “Tnum” and the Blackwell analytical “Tana” dimensionless solutions given by equation (10)(---581--10) . At high values of time, where equation (10)(---581--10) is valid, we conclude that there is no difference between the two solutions.

Figure 2. Dimensionless numerical and analytical wire evolutions (Bii = 10, A = 1.5, Z = A/2, γ = 5 × 10⁻³).

3. Inverse problem

For the inverse problem considered in this study, the effective thermal conductivity (λe), the effective volumetric heat capacity ((ρCp)e), and the heat transfer coefficient between the wire and the medium (hi) are regarded as unknown, while the other quantities appearing in the formulation of the direct problem described above are assumed to be known.

In order to estimate the above unknown parameters, we consider one temperature measurement. The estimation is based on minimizing the least squares norm: (---581--11) where (---581--12) Yi and Ti (P) are the measured and estimated temperatures, respectively, for time ti, i = 1, … , n. The estimated temperature is obtained from the solution of the direct problem, by using the current available estimate for the vector of unknown parameters P^T = [λe, (ρCp)e, hi].

4. The inverse problem solution

4.1. Estimation method

Many techniques have been presented, in the literature [10], to minimize the least squares norm (equation (11)(---581--11) ). Among these, the Levenberg–Marquardt [1,6,8–10] and the conjugate gradient methods [1,7] are particularly efficient for non-linear estimation problems. The so-called Levenberg–Marquardt Method was first derived by Levenberg [8] by modifying the ordinary least squares norm. Later Marquardt [9] derived basically the same technique by using a different approach. Marquardt's intention was to obtain a method that would tend to the Gauss method in the neighbourhood of the minimum of the least squares norm, and would tend to the steepest descent method in the neighbourhood of the initial guess used for the iterative procedure.

The iterative procedure to estimate the unknown parameters is given by: (---581--13) where ΔP^k is the increment of the vector of unknown parameters at iteration k.

The increment ΔP^k for the Levenberg–Marquardt Method can be written as: (---581--14) where μ^k is a positive scalar named damping parameter, and Ω^k is a diagonal matrix [1,10]. In our case we have considered Ω^k equal to the diagonal terms of [(X^k)^TX^k]. X is the sensitivity matrix defined as: (---581--15)

The purpose of the matrix term μ^kΩ^k, in equation (14)(---581--14) , is to damp oscillations and instabilities due to the ill-conditioned character of the problem, by making its components large as compared to those of X^TX, if necessary. The damping parameter is made large at the beginning of the iterations, since the problem is generally ill-conditioned in the region around the initial guess used for the iterative procedure, which can be quite far from the exact parameters. With such an approach, the matrix X^TX is not required to be non-singular in the beginning of iterations and the Levenberg–Marquardt Method tends to the Steepest Descent Method, that is, a very small step is taken in the negative gradient direction. The parameter μ^k is then gradually reduced as the iteration procedure advances to the solution of the parameter estimation problem, and then the Levenberg–Marquardt Method tends to the Gauss Method [6,10].

4.2. Sensitivity analysis

The sensitivity analysis is classically used for the optimal experimental design. It consists of analyzing the evolution of the different reduced sensitivity coefficients (---581----1) i,k = P^k(∂Ti/∂P^k) versus time.

These reduced sensitivity coefficients are calculated using a forward finite difference approximation for Ti : (---581--16) where δP^k is taken equal to 0.001·P^k for the parameters (λe, (ρCp)e, hi). This common value of 0.001 was sufficient to approximate all the derivatives.

4.3. Optimal experiment design

The most common criteria for the optimal experiment design are based on the information matrix X^TX, which summarizes the information content of an experiment [15,16]. It is necessary to have a great determinant of X^TX as a warranty for great sensitivity coefficients and no correlated parameters. This criterion, also named D-optimality, is used to minimize the hyper volume of the confidence region of the estimated parameters [17]. This confidence region is given by [10]: (---581--17) where V is the covariance matrix of the estimated parameters defined as [10]: (---581--18) (---581----2) is the vector with the estimated values for the parameters and (---581----3) is the chi-squared distribution for a given probability of the p estimated parameters. For a given value of (---581----4) , this equation describes a hyper ellipsoid, which has a hyper volume given by: (---581--19) where Γ(·) is the gamma function and det(V) = λ1λ2 ··· λp, with λi the ith eigenvalue of V.

Thus to minimize the hyper volume of the confidence region, the determinant of V should be minimized. This is equivalent to maximizing the determinant of V⁻¹ and leads to the D-optimality criterion, which maximizes the determinant of the information matrix X^TX.

However, the hyper ellipsoid can be skinny and long if one parameter has a very large variance compared to the others. So minimizing its volume may mislead the optimal design [17].

Another approach is to minimize the condition number of X^TX that can be taken as the ratio of its largest eigenvalue to its smallest one. The more this value is near one; the more the problem is well posed. The physical motivation of this approach also named modified E-optimality is that it optimizes the shape of the hyper ellipsoid (confidence region) by equalizing all its axes [18].

Therefore, a compromise between these two approaches can be made with the E-optimality that consists in maximizing the lowest eigenvalue of X^TX [19]. The physical motivation of this optimality is that it minimizes the largest parameter variance, and thus minimizes the major axis of the hyper ellipsoid [20].

5. Results and discussions

The determinant and the condition number will be analyzed in order to choose an optimal sensor position, which permits us to estimate the unknown parameter vector P^T = [λe, (ρCp)e, hi].

In this study, we have considered a cylinder filled with a soil (λe = 0.37048 Wm⁻¹K⁻¹, (ρCp)e = 1.004903 × 10⁶ Jm⁻³K⁻¹), the diameter and the height of the cylinder are, respectively, 32 and 24 cm. The used heat transfer coefficient between the hot wire and the soil is hi = 10 Wm⁻² K⁻¹.

The initial temperature of the medium is T0 = 290 K and the applied linear heat flux density is q = 6 kW m⁻¹.

5.1. Choice of an optimal position

The influence of the sensor position (R) on the determinant, the condition number and the lowest eigenvalue is plotted in figure 3.

Figure 3. Influence of the temperature sensor position (R) on the determinant, the condition number and the lowest eigenvalue.

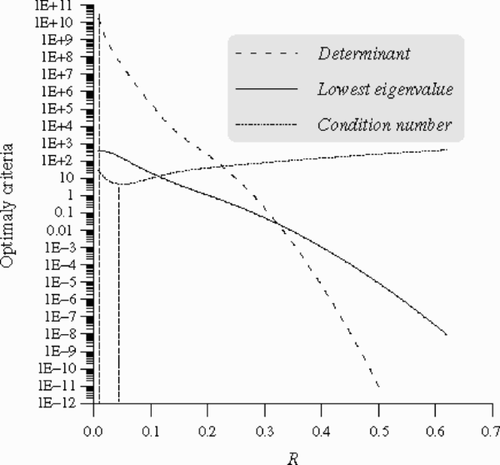
We see that the determinant has its maximum when R tends to zero. On the other hand, the condition number is minimal for R ≈ 0.045. A compromise between great determinant (information experiment) and low condition number (well conditioned information matrix) should be made. Thus, we have represented the E-optimality that maximizes the smallest eigenvalue of the information matrix X^TX. This criterion has a maximum for R = 0.0075 (figure 3). In this position the parameter estimation might be the best one and will be less sensitive to the measurement errors.

5.2. Parameter estimation on an optimal position

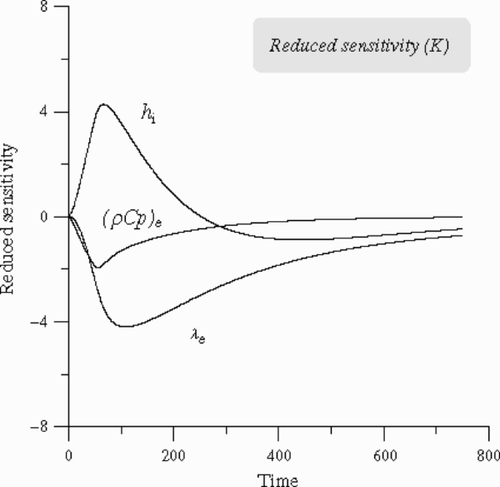
Considering the chosen optimal position of the temperature sensor (R = 0.0075), we perform a sensitivity analysis of the temperature to all parameters. We see (figure 4) that the reduced sensitivities, to the unknown parameters, vary in different manner and do not reach their maximums at the same time. So the considered parameters are not correlated.

Figure 4. Reduced sensitivities versus time.

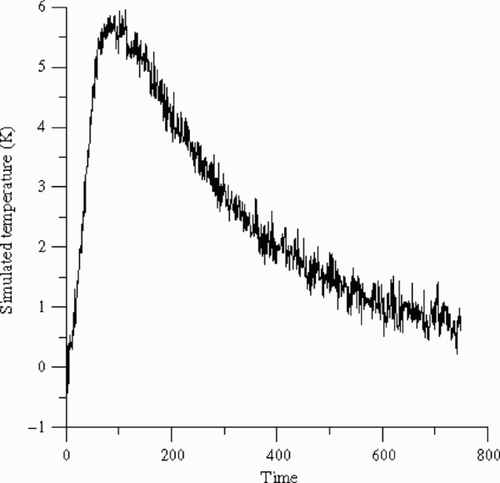
To demonstrate the validity and the accuracy of the inverse method the measured temperature is simulated. This temperature Ymeasured (figure 5) is obtained by adding a noise term ωσ to the computed exact temperature Texact (direct problem) as: (---581--20)

Figure 5. Measured temperature versus time (σ = 0.01 K).

The noise is Gaussian distributed and σ is the standard deviation of the measurement errors. Assuming 99% confidence for the measured data, ω lies in the range −2.576 ≤ ω ≤ 2.576 and it is calculated by a random generator [5,21].

The identification was performed for different standard deviations and initial values.

In table 1 we report the identification results for initial values varying between +10% and +90% of the expected value and for different values of noise standard deviation (σ = 0, 0.001, 0.1, 0.2 K).

Table 1. Identification results.

	λe(Wm^−1 K^−1)	(ρCp)e × 10^−6(Jm^−3 K^−1)	hi(Wm^−2 K^−1)
Expected values	0.37048	1.004903	10	Relative error (%)(---581----5)	Itera. Nb	Least squares J
Initial values (+10%)	0.407528	1.105393	11
σ = 0 K	0.370479	1.004904	10	1.28 × 10^−6	7	4.39 × 10^−11
σ = 0.01 K (0.2% Tmax)	0.370577	1.004451	10	2.37 × 10^−4	10	7.09 × 10^−2
σ = 0.1 K (2% Tmax)	0.371461	1.000370	10	2.39 × 10^−3	21	7.097
σ = 0.2 K (4% Tmax)	0.372441	0.995756	10	4.80 × 10^−3	6	28.39
Initial values (+30%)	0.481624	1.306374	13
σ = 0 K	0.37048	1.004903	10	0	9	5.05 × 10^−13
σ = 0.01 K (0.2% Tmax)	0.370577	1.004719	10	1.48 × 10^−4	17	7.09 × 10^−2
σ = 0.1 K (2% Tmax)	0.371462	1.000357	10	2.39 × 10^−3	17	7.097
σ = 0.2 K (4% Tmax)	0.345918	1.048558	10	3.78 × 10^−2	7	28.38
Initial values (+50%)	0.55572	1.507355	15
σ = 0 K	0.37048	1.004903	10	1.70 × 10^−8	6	2.39 × 10^−11
σ = 0.01 K (0.2% Tmax)	0.370577	1.004451	10	2.37 × 10^−4	10	7.09 × 10^−2
σ = 0.1 K (2% Tmax)	0.371454	1.000395	10	2.37 × 10^−3	10	7.097
σ = 0.2 K (4% Tmax)	0.314602	0.900846	10	4.74 × 10^−3	8	28.38
Initial values (+70%)	0.629816	1.708335	17
σ = 0 K	0.370479	1.004904	10	1.37 × 10^−6	22	4.50 × 10^−11
σ = 0.01 K (0.2% Tmax)	0.370579	1.004409	10	2.53 × 10^−4	35	7.09 × 10^−2
σ = 0.1 K (2% Tmax)	0.371454	1.000398	10	2.37 × 10^−3	17	7.097
σ = 0.2 K (4% Tmax)	0.372433	0.995912	10	4.74 × 10^−3	9	28.38
Initial values (+90%)	0.703912	1.909316	19
σ = 0 K	0.370479	1.004904	10	1.37 × 10^−6	66	4.68 × 10^−11
σ = 0.01 K (0.2% Tmax)	0.370578	1.004445	10	2.40 × 10^−4	78	7.09 × 10^−2
σ = 0.1 K (2% Tmax)	0.371454	1.000395	10	2.37 × 10^−3	28	7.097
σ = 0.2 K (4% Tmax)	0.372432	0.995914	10	4.74 × 10^−3	15	28.38

We notice that, without measurement noise, the relative error is less than 1.37 × 10⁻⁶%. This error increases with the measurement noise, but remains weak (4.8 × 10⁻³%) even with a standard deviation σ up to 4% of the maximal temperature (σ = 0.2 K).

On the other hand, the least squares norm J is very low (4.68 × 10⁻¹¹) for standard deviation equal to zero (σ = 0 K). Though, when σ ≠ 0 K, the least squares norm J increases linearly with σ². In fact: J ≈ nσ², in our case the number of the measurement n is equal to 750.

6. Conclusions

This numerical study has been performed using the hot wire method to estimate, simultaneously, the effective thermal conductivity, the effective volumetric heat capacity and the heat transfer coefficient between the wire and the medium from one temperature evolution versus time.

A sensitivity analysis has shown that a temperature sensor placed in the medium at a position near the hot wire permits us to estimate all the parameters simultaneously.

All the parameters quoted above have been estimated simultaneously. The results are accurate even with high measurement noise.

Nomenclature

Table

A	The cylinder aspect ratio, A = H/D
Bi	Biot number, (Bi = hD/λ)
Ci	The wire specific heat capacity (J kg^−1 K^−1)
Cpf	The fluid specific heat capacity (J kg^−1 K^−1)
Cps	The solid specific heat capacity (J kg^−1 K^−1)
Cp	Effective specific heat capacity (J kg^−1 K^−1)
D	The cylinder gap width, D = ro − ri (m)
g	Gravity acceleration (m s^−2)
H	Cylinder height (m)
h	Heat transfer coefficient (W m^−2 K^−1)
Ka	The medium volumetric heat capacity ratio
Ks	The hot wire volumetric heat capacity ratio
Mi	Linear wire mass (kg m^−1)
n	Number of measurements
q	Linear heat flux density (W m^−1)
Q	Reference heat flux density (W m^−2)
r, z	Space coordinates (m)
R, Z	Dimensionless space coordinates
t	Time (s)
T	Temperature (K)
p	Number of parameters

Greeks

Table

ε	Average porosity
θ	Dimensionless temperature, θ = (T−T0)/Tref
γ	Dimensionless wire radius, γ = ri/D
κ	Radius ratio, κ = ro/ri
ρ	Fluid density (kg m^−3)
λe	Effective thermal conductivity (Wm^−1 K^−1)
τ	Dimensionless time

Subscripts

Table

f	Fluid phase
h	High cylinder base
i	Inner wall (wire)
l	Lower cylinder base
o	Outer wall (ambient and initial)
ref	Reference
s	Solid phase
e	Effective