Multiparameter reconstruction for a stratified coating on a reflecting support

Abstract

We study the problem of reconstruction of multiparameters of an inhomogeneous slab on a perfectly reflecting support. Reformulating the reconstruction problem as a frequency domain inverse scattering problem on the half-line we prove the uniqueness of the reconstruction of two material parameters by two reflection coefficients corresponding to two different angles of incidence of the exciting plane electromagnetic wave. We develop reconstruction algorithms and demonstrate that simple approximate formulas give satisfactory reconstruction results.

Keywords:

• Inverse problem
• Inhomogeneous coating
• Electromagnetic reflection coefficients
• AMS Classifications: 34A55
• 78A46
• 35R30

1. Introduction

Consider an inhomogeneous coating of thickness h placed on a perfectly reflecting surface z = 0,  − ∞<x,y<∞. It is assumed that the dielectric permittivity ε and the conductivity σ of the coating depend on the space variable z only: ϵ =ϵ (z),σ =σ (z), 0≤ z≤ h. The external medium is assumed to be non-conducting and have a constant permittivity ε₀ and magnetic permeability μ₀ (the magnetic permeability of the coating is also assumed to be μ₀).

We consider the problem of the determination of ε and σ from exterior measurements of appropriately excited electromagnetic field. In the framework of frequency domain approaches, the data for the problem are functions of the field frequency. Potential applications of the present study concern the design of surface coatings with prescribed reflection properties in certain frequency ranges (for example, the design of non-reflecting coatings).

It is assumed that a plane linearly polarized harmonic wave (the TE-wave with the non-zero components E_x, H_y, H_z and the time dependence expiω t) impinges obliquely on the coating from the half-space z > h such that the wave vector of the exciting wave lies in the plane yz and forms an angle α with the negative z direction.

Maxwell's equations where (e_x, e_y, and e_z are the Cartesian basis vectors) yield the following differential equation for the component E_x of the total field in the half-space z≥ 0: (------117071--1) where (------117071--2) Since the plane z = 0 is perfectly reflecting, E_x must satisfy the boundary condition: (------117071--3) In the half-space z > h, E_x can be written (up to a factor independent of z) as (------117071--4) where R(ω ,α ) is the reflection coefficient; it is determined by the ratio of amplitudes of the reflected and incident waves.

The inverse problem is formulated as follows: given R(ω ,α ) as a function of ω, 0<ω <∞, for one or several values of the incidence angle α, determine ε(z) and σ(z) for 0<z<h.

Alternatively, introducing the impedance (------117071--5) (the last equality follows from the fact that the material parameters depend only on z) one may assume that the given characteristics of the field is the impedance measured on the surface z = h, i.e. Z_h(ω ):=Z(h,ω ). Then (4) and (5) yield (------117071--6) Thereafter, we will often omit the dependence on α for brevity. In what follows we will assume that σ (z)∈ L²[0,h],ϵ (z)∈ H¹[0,h] (i.e., dϵ/d z∈ L²[0,h]), and ϵ (z)>ϵ₀ for z∈ [0,h].

Exact methods for one-dimensional multiparameter inverse problems, both in the time and frequency domains, have been developed intensively since the 1970s; see, e.g., 1,2 for the time domain, and 3,4 for the spectral (frequency) domain. The review of results and references can be found in 5. Notice that in the spectral domain, inverse problems are usually formulated as inverse scattering problems on the whole axis: the data are, basically, the scattering (reflection and transmission) coefficients relating the so-called Jost solutions; these solutions are determined by the asymptotics as the space variable approaches +∞ and −∞.

In this article, we apply the method developed for the whole axis problems (see 5 and the references therein) to the analogous problems in a “half-axis” setting, where solutions of the governing equations have to satisfy prescribed boundary conditions at z = 0 (in 5, the solutions of the respective differential equations satisfy certain propagation conditions as z→±∞). The distinctive feature of these problems is that the analytical properties of the related scattering coefficients differ from those for the case of the whole line; particularly, the large frequency behavior is substantially different. Nevertheless, as we will show in the present article, the approach, after appropriate modifications, works for the inverse problem on the half-axis as well.

THEOREM 1

Two reflection coefficients R(ω ,α₁) and R(ω ,α₂) given as functions of ω, 0<ω <∞ determine uniquely the medium parameters ε(z) and σ(z), z∈ [0,h]. If one of the parameters is assumed to be known a priori, then the other parameter is determined uniquely by one reflection coefficient R(ω) corresponding to the single angle measurements.

2. Basic equations

First, we transform the governing equation (1) to the form of a differential equation with polynomial dependence on a spectral parameter, in which the leading term is independent of the space variable. Introducing the new variables (------117071--7) transforms (1) and (3) into the differential equation (------117071--8) with the jump conditions (------117071--9) and the boundary condition (------117071--10) Here (------117071--11) (------117071--12) Therefore, the discontinuity of ε(z) at z = h generates the jump conditions for u(x, λ ) in (8) and (9).

Introduce the reflection coefficient for systems (8–10) via the solution u(x, λ ) specified by its values for large for x>H. Since z=x+h − H for z > h (x > H), it follows that (------117071--13) We define the impedance for (8–10) by Note that if ϵ (h−0)≠ϵ₀, then has a jump discontinuity at x = H. Similar to (6), and are related as follows: (------117071--14) We want to reformulate the inverse problem as a problem of finding ϕ(x) and ψ(x). Note that neither H nor J are known, so the reflection coefficient for (8–10) is initially known only up to the factor exp 2iλ H.

The first step in our approach is the calculation of the reflection coefficient for an auxiliary problem given by the differential equation (8) on the whole half-line x > 0: the coefficients ϕ(x) and ψ(x) are the same as in the original problem, but there are no jump conditions (9). Then, we solve the inverse problem in the reconstruction of ϕ(x) and ψ(x) on the half-line x > 0 from the relevant reflection coefficient.

3. Auxiliary problem on the half-line

Consider the auxiliary problem (on the whole half-axis): (------117071--15) (------117071--16) (notice that ϕ (x)=ψ (x)=0 for x > H).

Let and be the relevant reflection coefficient and impedance, respectively. Since is a continuous function for all x > 0, we have, in particular, whereas (9) implies Since we have By (14) and the similar relation between and , we obtain, after simple algebra, (------117071--17) Finally, (13) and (17) give the relation between and the input data for the inverse problem, R(ω): (------117071--18)

PROPOSITION 1

The reflection coefficient R(ω) given for all ω > 0 determines uniquely H, J, and for .

Proof

Since ϕ(x) and ψ(x) are real-valued functions, for . Below we will show that approaches some real constant as λ → ∞. Then analyzing (18) as λ → ∞ gives H, J, , and, finally, for all λ.

Let u^±(x,λ) be the solutions of (15) specified by the asymptotics

PROPOSITION 2

(5,6) The solutions u^±(x,λ) have the following integral representations: (------117071--19) where the real-valued functions A^±(x,y)∈ H¹ are the (generalized) solutions of the Goursat problems (------117071--20) Let w(x,λ) be the solution of (15) satisfying the initial conditions Express w as a linear combination of u⁺ and u⁻: (------117071--21) where a(λ) and b(λ) can be written via the Wronskian, u,v:=uv′−u′v, of the solutions of (15): (------117071--22) Since the Wronskian of any two solutions, u and v, of (15) depends on x as we have Evaluating (22) at x = 0 and taking into account (19) gives (------117071--23) The immediate consequence of (23) is the following:

PROPOSITION 3

a(λ) and b(λ) are entire functions of exponential type satisfying and having the asymptotics (------117071--24) Moreover, (------117071--25) Now we note that (for all λ such that a(λ)≠ 0). Hence, (------117071--26) and (------117071--27) Equality (27) completes the proof of Proposition 1.

PROPOSITION 4

a(λ)≠ 0 for all λ such that Im,λ≤ 0.

Proof

Consider first . Let v(x,λ) be the solution of (15) such that v(0,λ) = 0 and for x ≥ H (equality (21) implies that v(x,λ) exists for all λ such that a(λ)≠ 0). Write (15) in the form (------117071--28) where , multiply this by and integrate with respect to x from 0 to H. Then, the integration by parts gives for the imaginary part of the resulting equation. Therefore, (------117071--29) Since g(x)>0 and ψ (x)≥ 0, the right-hand side of (29) is positive for all λ≠ 0 unless ψ (x)≡ 0. Therefore, (------117071--30) Since a(λ) and b(λ) cannot vanish simultaneously, (30) implies that a(λ)≠ 0 for .

Now, assuming that there exists λ₀=p+iq with Im,q<0 such that a(λ₀)=0, we have u⁻(0,λ₀)=0. On the other hand, u⁻(x,λ₀) vanishes exponentially as x → ∞. Manipulating with u⁻(x,λ₀) in the same way as it has been done above with w(x,λ), but integrating from 0 to ∞ and separating the real and imaginary parts of the resulting equation, we obtain two equalities: and Now it is easily seen that these equalities are in contradiction with g(x)>0, ψ (x)≥ 0, and the assumption that q<0.

4. Basic equation of the inverse problem

PROPOSITION 5

The solution w(x,λ) of (8) satisfying the initial conditions admits the following integral representation: (------117071--31)

Proof

Consider the solutions v^± (x,λ) of (15) fixed by the initial conditions Similar to (19), these solutions can be written as 5 Now and the representation (31) follows, with and .

The representation (31) implies, in particular, that λ w(x,λ)e^−iλ x is bounded in the half-plane λ :Im,λ≤ 0 for all x > 0. By (19) we can rewrite (21) as follows: (------117071--32) Multiply (32) by e⁻iλζ/(2πiλ) for ζ >x and integrate this with respect to λ from minus;∞ to +∞. Since 1/a(λ) has no singularities in the half plane λ:Imλ≤ 0, the Jordan lemma together with the residue theorem implies that the left-hand side vanishes for ζ >x>0. On the other hand, since A^± (x,y)=0 for y<x, the right-hand side can be written as where (------117071--33) (------117071--34) and one takes into account that A^± (x,y)=0 for y<x. By (23) we have that F(x)=Ω (x) = 0 for x>2H.

Therefore, we arrive at the equation relating the reflection coefficient and the integral kernels A⁺(x,y) and A⁻(x,y) (x∈ [0,H)): (------117071--35)

5. Reconstruction algorithms

In what follows, equation (35) will be used as a basis for the reconstruction algorithms.

5.1. Non-conducting medium

Consider first the particular case of the problem corresponding to a non-conducting medium: σ (z)≡ 0. Then the only function to be reconstructed is ε(z). Since, in this case, ψ (x)≡ 0, it follows that A⁺(x,y)≡ A⁻(x,y)=: A(x,y), and (35) becomes an integral equation for A(x,·), for every fixed x∈ [0,H): (------117071--36)

PROPOSITION 6

For every x∈ [0,H), equation (36) has a unique solution A(x,·)∈ H¹(x,2H−x).

Proof

Since, in this case, for , one can refer directly to the proof of the solvability of the related integral equation for the inverse scattering problem on the half-axis for the Sturm–Liouville equation 7.

Remark 1

Remark 1 In the case ψ≡ 0, equation (8) can be transformed to the Sturm–Liouville equation by using the transformation . The resulting potential in the Sturm–Liouville equation will involve the derivative dϕ/d x. But in the framework of our inverse problem, ϕ(x) is not necessarily differentiable; therefore, it is preferable to deal directly with equation (8).

The function to be reconstructed, , is related to A(x, x) as follows. The definition of ϕ(x) (12) together with (7) yields (------117071--37) where On the other hand, (------117071--38) Formulas (37) and (38) suggest the following reconstruction algorithm.

1.	Given R(ω ,α ) for one value of α, construct by (18).
2.	Calculate Ω(x) and F(x) by (33) and (34).
3.	For every x∈ [0,H), solve (36) and obtain A(x, x).
4.	Calculate x(z), 0<z<h as the solution of the differential equation
5.	Calculate by (------117071--39)

5.2. Conducting medium

In the general case of conducting medium, A⁺(x,y)≢ A⁻(x,y); therefore, a single equation (35) cannot determine separately A⁺ and A⁻. In this case, we use (35) to make a step in an iterative reconstruction procedure: A⁻ is determined by some approximation of the medium parameters, σ⁽ⁿ⁾(z) and ϵ⁽ⁿ⁾(z), via the solution of the direct problem, whereas A⁺ calculated from (35) gives the successive approximations, σ⁽ⁿ⁺¹⁾(z) and ϵ⁽ⁿ⁺¹⁾(z). Since A⁺(x,x) for a single α gives only ϕ−ψ (see (20)), which, in terms of the medium parameters, is a single relation for two parameters, in order to determine them separately we will use A⁺(x,x) corresponding to two different angles, α₁ and α₂. This requires the data, R(ω,α), to be given for two angles α=α₁ and α=α₂ .

The iterative reconstruction procedure consists of the following:

1.	Given R(ω;αk), k = 1, 2, calculate Ωk(x)=Ω(x,αk) and Fk(x)=F(x,αk) by (18), (33), and (34).
2.	Given the approximations σ(n)(z) and ϵ(n)(z), calculate ϕ(n)(x;αk) and ψ(n)(x;αk) by using (7) and (12) for α=α1 and α=α2 .
3.	Solve two problems (20) for A−(n)(x,y;αk), k = 1, 2.
4.	Use (35) to calculate A+(n+1)(x,x;αk) and :
5.	Set
6.	Set (------117071--40)
7.	Go to Step 2 with n↦n+1.

Remark 2

The iterative process may not converge on the whole interval [0,h); nevertheless, one can show that it converges on an interval z∈[h−l₁,h) for sufficiently small l₁ 8. The latter is based on the fact that the mapping , z∈[h−l₁,h) is a contraction in the functional space , with some C > 0.

Having ε(z) and σ(z) reconstructed on [h−l₁,h], one can “strip off ” the layer [h−l₁,h] by re-calculating the reflection coefficients in such a way that the new reflection coefficients correspond to a medium occupying the slab z∈[0,h−l₁] with the same material functions ε(z) and σ(z). To do this, calculate first the impedance Z(z,ω) at z=h−l₁ as the solution of the differential equation on the interval [h−l₁,h] with the given boundary condition Z(h,ω) = Z_h(ω) at z = h; then the new reflection coefficient is given by (6) where h is to be replaced by h−l₁.

Applying again the reconstruction procedure with the new reflection coefficients gives ε(z) and σ(z) for z∈[h−l₂,h−l₁] with some l₂ < l₁; repeating this, we reconstruct ε(z) and σ(z) on the whole interval [0,h] in a finite number of steps, because the length of subsequent intervals of reconstruction, l_j−l_j+1, can be chosen to be uniformly bounded from below by a positive constant (determined by an appropriate norm of R(ω) and C).

Remark 3

If one of the medium parameters, ε(z) or σ(z), is assumed to be known a priori, then the medium parameter to be determined is uniquely related to ϕvarphi;−ψ; thus, the knowledge of the reflection coefficient for a single angle of incidence is sufficient for the iteration procedure.

Remark 4

In the case of slowly varying, low conducting media (dϵdz≪1 and σ≪1), appropriate approximations for A⁺(x,x) provide simple approximate formulas for ε and σ. For example, if ϵ(z)≡ϵ₀ , the “zero order approximation” A⁺(x,x)≈−F(2x), see (35), gives for σ(z) (in the case of the normal incidence, α = 0) the following formula (------117071--41) (assuming that the data are available in the frequency range 0<ω <M).

Similarly, in the case σ (z)≡ 0, an approximate formula for ε(z) follows from (39) for small A: (------117071--42)

6. Numerical examples

The following examples illustrate the numerical performance of the proposed approach. Figure 1 shows the reconstruction of a single medium parameter provided that another parameter is known. To avoid the “inverse crime”, we choose the true profiles of the parameters (to be reconstructed by applying the proposed approach), so that the corresponding coefficients in (8) and (15), ϕ(x) and ψ(x), are piece-wise constant functions. This allows calculating the associated reflection data analytically, in the closed form. Then we treat these data by the inverse algorithms described above (more precisely, by simple “truncated” algorithms suggested by the theory developed above), and compare the reconstructed profiles with the true ones.

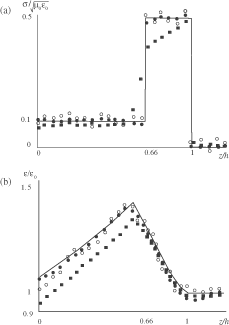
Figure 1. One-parameter reconstruction: (a) reconstruction of σ(z) (ϵ≡ϵ₀) and (b) reconstruction of ε(z) (σ≡ 0). The solid lines are for the true profiles, ▪ is for the reconstruction by using the approximate formulas (41) and (42), ○ is for the reconstruction by using the “first order approximation”, and ◯ is for the reconstruction by using the “first order approximation” in the presence of a 5% noise in the reflection coefficients.

Figure 1(a) illustrates the reconstruction of σ(z) in the case ϵ(z)≡ϵ₀ . The reflection coefficient corresponding to the two-layer conductivity, is given by (------117071--43) where , j = 1, 2, Figure 1(a) presents the reconstruction of σ by the approximate formula (41) as well as by the “first order approximation”: by (20) we set ; in turn, by (35), we set and where A⁻(x,y) is the approximate solution (involving two terms of the Neumann series) of the system of integral Volterra equations equivalent to the Goursat problem (20) (see, e.g., 9) with ϕ≡0 and being the initial guess for σ.

Figure 1(b) illustrates the reconstruction of ϵ(z) in the case of non-conducting medium: σ (z)≡ 0. The profile corresponds to ϕ in (15), which is piece-wise constant: with The corresponding reflection coefficient is given by where , j = 1, 2, Figure 1(b) presents the reconstruction of ϵ by the approximate formula (42) as well as by the “first order approximation” for A(x, x) in (39).

In Figure 2, the simultaneous reconstruction of both the medium parameters is presented, in the case of a two-layer covering with the parameters and The corresponding reflection coefficients are given by (43) with Figure 2 illustrates the reconstruction by the zero order approximate formulas that follows from (40): , so that (------117071--44)

Figure 2. Simultaneous reconstruction of ε(z) and σ(z) by the approximate formulas (44). The solid lines are for the true parameters, ▪ is for the reconstruction.

7. Concluding remarks

We propose an approach to the electromagnetic coating design problems based on the inverse scattering problem on the half-line. We prove uniqueness of the reconstruction of multiparameters of a stratified coating by the reflection coefficients, as functions of the frequency, corresponding to an appropriate excitation of the medium. The reconstruction algorithms are based on the analysis of the integral equation (35) relating the reflection data and the medium parameters.

The numerical examples show that the reconstruction is satisfactory even in the case of using simple approximate formulas suggested by the approach. Notice that these approximations are satisfactory even for non-smooth and rather contrast profiles of the parameters. Therefore, they can be used as good first approximations when using other reconstruction procedures (e.g., the ones based on the optimization approach 10).