The energy-free equations of the 3D inverse problem of dynamics

Abstract

Given a two-parametric family of curves f(x,y,z) = c1, g(x,y,z) = c2, we look for potentials V under whose action a particle of unit mass can describe the curves of the family. Using a procedure inspired by Kasner, who studied the geometrical properties of the trajectories, we obtain two partial differential equations satisfied by V. These equations do not contain the total energy, which appeared in Szebehely-type ones, and relate merely the potential and the given family. Therefore they can be used when no information on the energy is given in advance, as well as for the direct problem of dynamics. The case of the general autonomous force fields is also discussed.

Keywords:

• Spatial inverse problem of dynamics
• Energy-free equations
• Conservative systems

1. Introduction

The version of the inverse problem of dynamics considered here is: given a two-parametric family of curves in (---545----1) , find the force field (conservative or not) under whose action a material point of unit mass describes, with suitable initial conditions, the curves of the family.

Both the planar (2D) and the spatial (3D) inverse problems of dynamics for general force fields have been considered by Dainelli [1] in the same article, from which Whittaker ([2], p. 93) included in his book only the 2D version. The 2D problem, this time for conservative systems, has renewed the interest in the inverse problem of dynamics by means of Szebehely's [3] partial differential equation relating the potential to a monoparametric family of curves and to the total energy. Similar results for the spatial problem were to appear almost a decade later. Another basic result for the 2D inverse problem was the energy-free partial differential equation obtained by Bozis [4] from Szebehely's equation, and later derived directly by Anisiu [5]. A similar derivation of the basic equations will be given here for the case of spatial families of curves.

Beside the 2D problem, Dainelli [1] studied the existence of a general force field (not necessarily conservative), which can produce as orbits two-parametric 3D curves of the form (---545----2) or, more generally, (---545--1) Actually he referred to a single curve (c1 = c2 = 0), but working with the differentials of ϕ and ψ, respectively of f and g, his results are valid in fact for two-parametric families of curves.

For conservative systems, the 3D problem was tackled by Érdi [6] for a monoparametric family of orbits, and then for two-parametric families by Váradi and Érdi [7]. They obtained partial differential equations satisfied by the potential V, supposing that the total energy of the particle was known; therefore the energy appears in the equations, as in the case of Szebehely's equation for monoparametric 2D families. Puel [8] used the least action principle of Maupertuis to obtain the equations of the 3D inverse problem of dynamics. Because in this case the potential appeared as a solution of two partial differential equations, the existence of such a potential and its relation with the energy was the subject of further studies, like those of Gonzáles-Gascón et al. [9], Bozis and Nakhla [10] and Shorokhov [11]. Puel obtained in [12] the intrinsic equations of the 3D inverse problem, using the Frenet reference frame and revealing interesting geometrical properties. Partial differential equations satisfied by the force components for general force fields were given in [13]. A review of the basic results in the inverse problem of dynamics, including the 3D ones, was presented in [14] by Bozis.

In what follows we derive in a systematic way, considering all the cases that might occur, the energy-free equations for the conservative 3D fields, as we have done for the 2D problem in [5]. We present the spatial region where real motion is allowed, as well as the equations that relate the total energy E, the potential and the given family. Equations (12)(---545--12) and (14)(---545--14) were written as such and used recently to find homogeneous potentials compatible with homogeneous families of orbits by Bozis and Kotoulas [15]. The inverse problem for 3D families of straight lines (equations (10)(---545--10) and (11)(---545--11) ) was considered by Bozis and Kotoulas [16]. The 3D inverse problem for a general force field was solved in 1880 by Dainelli [1]. Bozis [13] obtained equation (46)(---545--46) , which relates several derivatives of the components X,Y,Z of the force field. Maybe the recent results in the 2D inverse problem, based on the corresponding energy-free equation, as well as the interest in various 3D potentials, have stimulated the research on similar tools for the 3D inverse problem.

The energy-free equations derived in section 2 are applied to find the potentials, the energy and the regions where the motion is possible for two specific families of curves. In section 3 an application involving families of curves created by the 3D Hénon–Heiles type potential is given.

2. The equations of the 3D inverse problem for conservative fields

We consider the 3D family of curves (1)(---545--1) with f, g of C³-class (continuous with continuous derivatives up to the third order on a domain in (---545----3) ) and such that at least one 2 × 2 minor of the Jacobian matrix (∂(F,G)/∂(x,y,z)) does not vanish. In what follows we shall suppose that locally (---545--2) where the subscripts denote the corresponding partial derivatives. Of course, if any other determinant (containing derivatives with respect to x and y, or to x and z) is different from zero, one can proceed similarly.

The inverse problem under consideration is: find the potential V(x,y,z) of C²-class under whose action, for appropriate initial conditions, a material point of unit mass, whose motion is described by (---545--3) will trace the curves of the family (1)(---545--1) (the dots denote derivatives with respect to the time t). The potential will be defined on a 3D domain whose points belong to one and only one curve from the family (1)(---545--1) .

In order to obtain the equations satisfied by V, we shall eliminate the time derivatives of x, y, and z following the procedure used by Kasner [17]. To this aim we differentiate equations (1)(---545--1) with respect to t, and from (---545---1) we get (---545--4) where (---545--5)

The notation (5)(---545--5) was introduced in [16], where it was emphasized that the family (1)(---545--1) leads to a unique pair α, β and, conversely, the pair α, β determines uniquely the family (1)(---545--1) .

Differentiating both relations in (4)(---545--4) we get (---545--6) This is denoted by (---545--7) and reminding (4)(---545--4) into account, we obtain from relations (6)(---545--6) (---545--8) Making use of (4)(---545--4) again and the equations of motion (3)(---545--3) , we get (---545--9)

Our aim being to obtain differential equations satisfied by V, we have to analyse some special cases.

Case 1 A = B = 0. It is obvious that, in view of relation (8)(---545--8) , it also follows that (---545----4) , hence the curvature (---545----5) of each member of the family (1)(---545--1) vanishes. We denote (---545----6) by (---545----7) , where (---545----8) are unit vectors along the axes Ox, Oy, Oz.

It follows that we have A = B = 0 if and only if the family (1)(---545--1) consists of straight lines. This case was analysed in detail by Bozis and Kotoulas [16]. Relations (9)(---545--9) give rise to two linear partial differential equations to be necessarily satisfied by V, namely (---545--10) These equations will admit a solution only if α and β satisfy, besides the two equations obtained from (7)(---545--7) for A = B = 0, a supplementary equation (---545--11) So, generally, the inverse problem is not expected to have a solution for arbitrary families of straight lines.

Case 2 A ≠ 0 and B ≠ 0. By eliminating (---545----9) between the two relations in (9)(---545--9) we obtain first a necessary condition to be satisfied by V, (---545--12) where α,β from (5)(---545--5) and A, B from (7)(---545--7) depend on the derivatives of f and g up to the second order. Because of (---545----10) , it follows that the motion is possible only in the region determined by (---545--13)

Differentiating both members of the equality (---545----11) with respect to t and replacing (---545----12) from the first equation in (3)(---545--3) , respectively (---545----13) and (---545----14) from (4)(---545--4) , we obtain a second differential relation to be satisfied by V (---545--14) where (---545--15)

Summarizing the above reasoning, we assert that a potential that produces as orbits the curves of the family (1)(---545--1) satisfies by necessity the two differential relations (12)(---545--12) and (14)(---545--14) , the motion of the particle being possible in the region determined by inequality (13)(---545--13) . We remark that equation (14)(---545--14) is of second order in V and does not involve the energy (constant on each curve of the family), hence it is the corresponding equation for the 3D case of Bozis' equation [4] satisfied by planar potentials. The planar equation was derived directly by an elimination process of the derivatives of x(t) and y(t) between some differential relations based on the equations of motion and on the given planar family by Anisiu [5].

In the following we shall derive the equation from which the total energy can be expressed. Denoting by (---545--16) one can check by direct calculation that (14)(---545--14) is equivalent to (---545--17) The characteristic system for (17)(---545--17) is (---545---2) and one easily obtains (---545----15) and (---545----16) . It follows that f(x,y,z) = c1 and g(x,y,z) = c2 are integrals, hence the general solution of (17)(---545--17) is W = E(f,g) with E an arbitrary function.

In view of relations (4)(---545--4) and (9)(---545--9) , we get from (16)(---545--16) that (---545--18) i.e. W = E(f, g) is the total energy, constant on each curve of the family (1)(---545--1) . It follows that the equation (---545--19) which was derived by Váradi and Érdi [7] using the energy integral (and which corresponds to Szebehely's planar equation), can be obtained as a consequence of the second order partial differential equation (14)(---545--14) .

The two equations (12)(---545--12) and (14)(---545--14) for a single unknown function V will not always have a solution; the compatibility conditions are to be checked. The advantage of this formulation consists in the fact that it is free of energy, and one can search for potentials in several classes, which are of astronomical or physical interest, as for example homogeneous (Bozis and Kotoulas [15]) or quasihomogeneous ones.

Remark The fact that equations (12)(---545--12) and (14)(---545--14) do not contain the energy makes them suitable for the direct problem of dynamics: given a 3D potential, find families of orbits of the form (1)(---545--1) generated by it. We can rearrange the mentioned equations and obtain a linear partial differential equation of first order in α and β (---545--20) and a nonlinear one of second order (---545--21) Case 3 B = 0 and A ≠ 0. From the first relation in (9)(---545--9) we obtain again inequality (13)(---545--13) ; instead of (12)(---545--12) , the relation (---545--22) holds, beside the second order partial differential equation (14)(---545--14) , which can be derived as in Case 2. The energy is given by (19)(---545--19) .

Case 4 A = 0 and B ≠ 0. The inequality to be satisfied is (---545--23) and (12)(---545--12) is replaced by (---545--24) Starting with (---545----17) , we follow the steps from the case when both A and B were different from zero and obtain instead of (14)(---545--14) (---545--25) where (---545--26) The energy is given in this case by (---545---3) Synthesis Given a two-parametric family of curves (1)(---545--1) , we compute α and β from (5)(---545--5) , and A and B from (7)(---545--7) . We obtain the partial differential equations satisfied by the potential V, which are:

Case 1 (A = B = 0): (10)(---545--10) ;

Case 2 (A≠B ≠ 0): (12)(---545--12) and (14)(---545--14) ;

Case 3 (A ≠ 0, B = 0): (22)(---545--22) and (14)(---545--14) ;

Case 4 (A = 0, B ≠ 0): (24)(---545--24) and (25)(---545--25) .

Example 2.1 We consider the two-parametric family of curves (1)(---545--1) with (---545--27) For this family we have (---545---4) The first-order equation (12)(---545--12) in Case 2 reads (---545---5) and has the general solution (---545--28) The second-order equation (14)(---545--14) is (---545--29) Substituting V from (28)(---545--28) in (29)(---545--29) , and denoting by (---545---6) we obtain (---545--30) It follows that we must have (---545---7) which gives v(u,w) = F1(u + 2w) + uF2(u + 2w), with F1,F2 arbitrary functions. Introducing this value of v(u, w) in the right-hand side of (30)(---545--30) and equating it with zero leads to (---545----18) where C is an arbitrary constant. We finally get (---545---8) From (19)(---545--19) we obtain the energy E = 4C; the inequality (13)(---545--13) becomes (---545----19) .

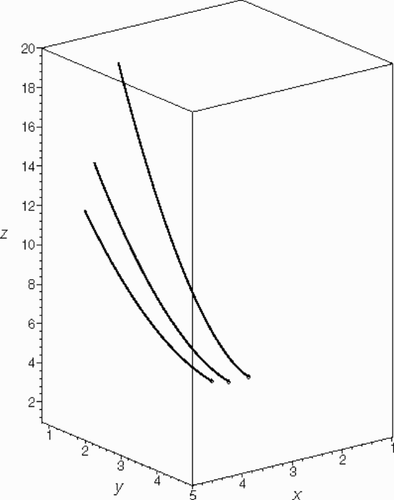
We remark that for (---545----20) and C = 0 we have (---545--31) and E = 0; condition (13)(---545--13) gives no restriction for the domain where the particle moves. In figure 1 three curves of the family (27)(---545--27) are plotted traced under the action of the potential (31)(---545--31) . The curves pass respectively through the points (1,1,1), (1.4,1,1) and (1.6,0.8,1), and the initial velocities for the system (3)(---545--3) are obtained from (9)(---545--9) and (4)(---545--4) .

Figure 1. Curves of the family (27)(---545--27) produced by the potential (31)(---545--31) .

Example 2.2 For the two-parametric family of elliptic orbits given by (---545--32) with a priori energy given (---545----21) , Váradi and Érdi [7] and Bozis and Nakhla [10], have found the central potential (---545----22) , which gives rise to the curves of the family (32)(---545--32) . For this family we have (---545---9) hence it enters Case 3. Relation (22)(---545--22) becomes (---545---10) with the general solution (---545--33) We substitute V from (33)(---545--33) in (14)(---545--14) and get (---545--34) where w = x² + z², (---545----23) .

It follows that d11 = 0; its general solution is (---545----24) . By substituting this in (34)(---545--34) we obtain (---545--35) This equality is possible if and only if each member is equal to a constant k0. It follows that (---545---11) or (---545--36) From (19)(---545--19) we obtain the energy (---545---12) Real motion is possible only in the region (13)(---545--13) , which is described in this case by (---545---13) For the particular case k0 = 4, C1 = C2 = 1/2, the potential (---545--37) will give rise to the curves of the family (32)(---545--32) . In figure 2 the curves of that family passing through the points (1.1,1,1), (1.05,1.05,1) and (1,1,1.1) are shown. They are traced by a unit mass particle with initial velocities calculated from (9)(---545--9) and (4)(---545--4) .

Figure 2. Curves of the family (32)(---545--32) produced by the potential (37)(---545--37) .

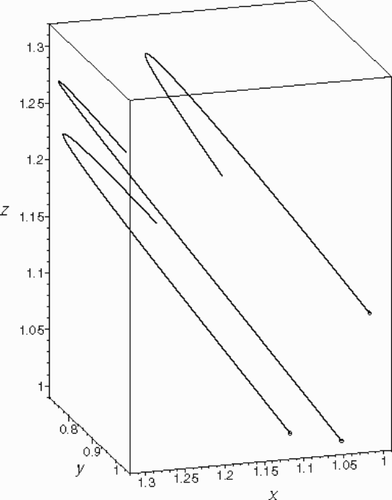
It can be checked that the potential and the prescribed energy given by Váradi and Érdi [7] follow from our result for k0 = 4, C1 = C2 = 0. Using the energy-free equations we have obtained a larger class of potentials, which can give rise to the elliptic orbits (32)(---545--32) .

3. Application to cubic potentials

The family of Hénon–Heiles 3D potentials (---545--38) with at least one of a, b, c different from zero, consists of cubic perturbations of harmonic oscillators. These potentials have been intensively studied lately, due to their applicability in various fields of physics; e.g., they describe the motion of the nuclei in small molecules [18], as well as the motion in the central region of a galaxy [19].

Considering the 2D case, Anisiu and Pal [20] showed that, out of the families of curves (---545----25) , only two are compatible with potentials of Hénon–Heiles type, namely:

1.	the family (---545----26) with (---545----27) ;
2.	the family (---545----28) with (---545----29) .

We shall apply the results in section 2 to study the following problem: are there two-parametric families of curves (1)(---545--1) with (---545--39) compatible with a cubic potential of the form (38)(---545--38) ?

For the family (39)(---545--39) we have (---545---14)

First we consider the case r = s ≠ 1, for which A = 0 and B ≠ 0. The first-order equation satisfied by V is in this case (24)(---545--24) ; it holds if and only if (---545----30) and b = c. The second order equation (25)(---545--25) is satisfied for:

1.	(---545----31) ; this means that the family (---545----32) is compatible with the potential (---545--40)
2.	(---545----33) ; in this case the family (---545----34) is compatible with (---545--41)

If r ≠ s,r ≠ 1 we have A ≠ 0,B ≠ 0, and from equation (12)(---545--12) it follows a = b = c = 0, hence no cubic potential is compatible with a family of the form (39)(---545--39) . The same situation arises when equation (10)(---545--10) are used for the family of straight lines obtained for r = s = 1, as well as for 1 = r ≠ s (when B = 0 and A ≠ 0, and we use equation (22)(---545--22) from Case 3 in section 2).

We remark that both cubic potentials (40)(---545--40) and (41)(---545--41) that are compatible with families of the form (39)(---545--39) consist of an anisotropic harmonic oscillator, the first one having an axially symmetric perturbation and the second one a 1D cubic perturbation.

4. The case of a general force field

Let us consider a system of the form (---545--42) the force components X , Y and Z being of C¹-class on a domain in (---545----35) . The differential equations of the trajectories of (42)(---545--42) , and the geometrical properties of these trajectories, were obtained by Kasner [17].

The reasoning in section 2 can be applied for the system (42)(---545--42) too; we remind the notations α, β in (5)(---545--5) , and A, B in (7)(---545--7) , which are related to the given family of curves (1)(---545--1) .

If the family (1)(---545--1) consists of straight lines, i.e. A = B = 0, instead of (10)(---545--10) we have (---545--43) These are the relations satisfied in this special case by the components X, Y, Z of the force. It follows that X can be an arbitrary function, and then Y = αX, Z = βX.

Let us consider now A ≠ 0, B ≠ 0. A first relation is obtained from (---545----36) , namely (---545--44) The positivity of (---545----37) implies that the region where the motion is allowed is (---545--45) By differentiating (---545----38) with respect to t and by using (42)(---545--42) and (4)(---545--4) we get (---545--46) where p, q, l, m are given by (15)(---545--15) . This partial differential equation, as well as the algebraic relation (44)(---545--44) , has been obtained, with different notation in [13]. We remark that, if we denote by (---545--47) equation (46)(---545--46) can be written as (---545---15) or (---545--48) From relation (47)(---545--47) we then get (---545--49) and from (44)(---545--44) (---545--50) Therefore in the general case the inverse problem always has solutions; for an arbitrary positive function ξ, we obtain the components of the force, given by (48)(---545--48) –(50)(---545--50) , which can produce as orbits the curves of the two-parametric family (1)(---545--1) .

The situation when only one of A and B is identically null can be treated similar to that in section 2 for conservative fields.

To end this journey through the 3D inverse problem we remind the formulae for the force components as given in [1], namely (---545--51) where (---545----39) is an arbitrary function of the three variables x, y, z, and (---545----40) . We put a tilde on Dainelli's notation in order to avoid confusion with ours. The expressions in (51)(---545--51) can be obtained from (48)(---545--48) to (50)(---545--50) by replacing (---545----41) with δ from (2)(---545--2) ; it will follow that (---545----42) and (---545----43) , with (---545----44) from (5)(---545--5) .

5. Conclusions

Generally, the 3D inverse problem of dynamics gives rise to two energy-free partial differential equations (of first and second order) satisfied by the potential, and to an inequality, which determines the region in space where real motion is possible. These are deduced in a natural way following the ideas of Kasner [17]. The relation between conservative and nonconservative case is also clarified.

The examples in section 2 use the energy-free equations to obtain all the potentials, which give rise to a given two-parametric 3D family of curves. In section 3 we provide two families of curves compatible with 3D cubic potentials (perturbations of anisotropic oscillators).

Families of more complicated orbits can be described in parametric form; this fact justifies further studies in order to extend the 2D results of Bozis and Borghero [21] for conservative systems, respectively of Anisiu and Pal [22] for general force fields.

Acknowledgement

The author thanks the referees for their valuable suggestions.

Additional information

Notes on contributors

Mira-Cristiana Anisiu *

Email: [email protected]

Notes

Email: [email protected]