Linear regularization algorithms for computer tomography

Abstract

The problem of image reconstruction of the multicomponent structure based on indirect boundary observations is considered. The image of the distribution of desired characteristics is described inside the plane domain by a two-dimensional function. A new transformation (related with the classic Radon transformation) for a mathematical modeling of the traditional measurement scheme in computer tomography is proposed. Some linear integral–differential equation of the first kind is derived as a basic equation. This equation leads to the linear method for the desired image reconstruction. Regularization spline algorithm for numerical realization of the proposed method is constructed and demonstrated with the numerical experiments on the simulated examples, related to the electric tomography.

Keywords:

• Image reconstruction
• Electrical tomography
• Spline
• Regularization

1. Introduction

Computer tomography consists in reconstruction of the image of the interior of a body using the measurements, on its surface, of characteristics of some external field. Frequently, this problem of the reconstruction can be mathematically stated as a coefficient inverse problem for a differential equation describing the distribution of the field in the considered region. Coefficients are functions of the space variables and characterize properties of a medium. Well known tomographies are: X-rays, ultrasonic, radioisotope, infrared and the electrical impedance tomographies. For example, X-ray tomography leads to the linear mathematical model and corresponding linear algorithms can be used for its solution but the known methods for the electrical impedance tomography (EIT) imaging are nonlinear [1,2].

We propose here another approach for the mathematical modeling of the measurement of the external data. We explain it here for a plane case. The proposed model of the measurement scheme in the radial symmetric case leads to the classic Radon transformation [3,4]. In the general case, we introduce a new G-transformation, related with the Radon transformation. We obtain the basic integral–differential equation and a basic mathematical model. The algorithm for regularization of the proposed model is constructed. This approach and stability of the algorithm are demonstrated with the numerical experiment on the simulated model problem.

2. General ray principle and the basic integral–differential equation

Let us consider the problem of image reconstruction of a structure, consisting of components with different characteristics, under the influence of known external physical field or rays. The image of the distribution of these characteristics are described inside the plane domain Ω with a boundary Γ by a function g(x,y), that must be reconstructed based on indirect boundary observations. To construct a method for the desired imaging, we propose here the general ray (GR) principle that formalizes a mathematical model of the traditional measurement scheme – parallel scanning beam. GR-principle consists of the following assumptions:

1.	the considered influence of the external physical field or rays can be simulated mathematically by the plane vector field (--1) parallel to the direction along the straight line l;
2.	the field (--2) is characterized with some function u(x,y);
3.	we can measure the values of the difference ν (P1,P0)=u(x1,y1)−u(x0,y0) in any of the boundary points P1=(x1,y1) and P0=(x0,y0) of the domain.

The aforementioned tomographies such as electrical, ultrasonic, infrared and radioisotope imaging [1] can be considered under this GR-principle due to the choice of the measurement scheme.

Let the line l have the parametric presentation p=x cosϕ +y sinϕ, where |p| is the length of the perpendicular, passing from the origin of coordinates to the line l, and ϕ is the angle between the axis x and this perpendicular. Hence, using this parametrization, we present the function ν =ν (pϕ). Then using the Radon transformation [3] for the derivative (--3) of the function u along the line l: (1) (2) (3) we have as the mathematical model of the GR-principle G-transformation, defined by the formula (4) where (--4) and (--5) are derivatives of the function u on variables x and y. If the function ν (p,ϕ) is given for all p,ϕ we can obtain the linear basic integral–differential equation (5) of the first kind with respect to the function u(x,y).

It is clear that the basic equation does not include directly the desired reconstruction function g(x,y), hence, it is not sufficient for the solution of the considered problem. It might be used together with the mathematical model of the distribution of the field (rays) (--6) , i.e. together with an equation including g(x,y). We shall demonstrate this scheme for electrical tomography.

3. Application to electrical tomography

Electrical tomography consists in reconstructing the image of the interior structure of the body on the measurements of electrical characteristics made on its surface [1,2]. The well known and the most developed approach is the electrical impedance tomography (EIT), which includes the resistance and capacitance tomographies. In a plane case, EIT can be mathematically described as a coefficient inverse problem for the Laplace equation written in the divergent form (6) where x,y∈Ω. Some open region on a plane u(x, y) is the potential and the function T=T(x,y) characterizes the conductivity or admittivity of a media. The goal of EIT is to reconstruct the distribution of functions that characterize the internal structure of the object, on the measurements on the surface. The known approaches for the solution of EIT lead to nonlinear ill-posed problems.

We consider here the mathematical model of another variant of the electrical tomography, when the external homogeneous electromagnetic field (--7) initiates some distribution of the electric potential inside the domain Ω. The idea is to use the basic equation together with the model (6)(6) and some boundary conditions in order to obtain the linear method for the reconstruction of the desired function.

For simplicity, we define the domain Ω as an unit circle. Using the parametrization (2)(2) and (3)(3) for the line l, we shall define the potential, initiated by (--8) as u(x,y,ϕ). To be more concrete, we will consider the model corresponding to the capacitance tomography, when the function g(x, y) is the permittivity function: g(x,y)=T(x,y)= ϵ(x,y). For every fixed ϕ, we have an equation (7) We suppose also that for every fixed ϕ, we know the functions Jn(x,y,ϕ), u⁰(x,y,ϕ) on the curve Γ and the next boundary conditions are satisfied: (8) (9) where (--9) is the normal derivative in the points of the boundary curve Γ In problems (7)(7) –(9)(9) , both functions u(x,y,ϕ) and ϵ (x,y) are unknown, and the solution of the problem in a general case is not unique. The investigation of classes of the solution of similar problems is presented, for example, in [5]. As we shall demonstrate, equations (7)(7) –(9)(9) together with the basic equation (5)(5) can be resolved uniquely with respect to the pair of functions u, ϵ. We shall call the system of equations (5)(5) , (7)(7) –(9)(9) the basic mathematical model.

It is clear that from equation (9)(9) we can obtain, in accordance with a parallel beam measurement scheme, the data ν (p,ϕ) corresponding to (5)(5) , where p∈[−1,1], ϕ∈[−π/2,π/2], when x,y∈Γ. Hence, we can use GR-principle and basic equation (5)(5) . Let us substitute variables with formula: (-1) and reduce the problem (7)(7) –(8)(8) to the Neumann problem (10) (11) for every fixed ϕ with respect to the one unknown function v(x,y,ϕ). Solution of this problem to within an arbitrary constant c is presented for (x,y)∈Ω by formulae (12) (13) which gives possibility to calculate derivatives (--10) and (--11) uniquely. Then we use formulae (-2) and substitute (--12) into the basic equation (5)(5) . Denoting γ (x,y)≡ 1/ϵ (x,y) we obtain a linear integral equation with respect to the function γ (x,y): (14) The solution of equation (14)(14) is possible when the inverse operator (--13) for the operator (--14) exists (we will present such an example below). In this case we shall say that the operator (--15) defines G-method.

4. Penetrating tomography – tomography without scanning

Now we shall present one variant of the basic mathematical model that is based on the one time influence of the external field without scanning. For such a situation, the potentials u and v in formulae and explications above do not depend on the scanning angle ϕ except the function ν (p,ϕ), but it has a new interpretation. We will define this function as a difference ν (P1,P0)= u⁰(x¹,y¹)−u⁰(x⁰,y⁰) of known values of the boundary function u⁰(x,y) from the condition (9)(9) , in boundary points P1=(x¹,y¹) and P0=(x⁰,y⁰) that belong to the straight line with the parametrization (2)(2) –(3)(3) for all values of the parameters p∈[−1,1],ϕ∈[−π/2,π/2]. So, we have the function ν (p,ϕ) that is just another recalculated form of the Dirichlet boundary condition. But now, we have the analog of the equation (14)(14) , where (--16) and (--17) do not depend on the parameter ϕ So, we can use G-method, that gives the possibility of reconstruction of the function γ (x,y). It is very important that one act of the external field influence, one penetration of the field into the body with corresponding boundary measurements, give us the possibility of solving the inverse problem being considered. That is why we call such procedure penetrating tomography.

We can now write the auxilar Neumann problem (10)(10) –(11)(11) in the form that does not depend on ϕ (15) (16) with respect to the unknown function v(x, y).

We propose here a new method for constructing the solution v(x, y) of the auxilar Neumann problem (15)(15) –(16)(16) , different from the Green formula (12)(12) . To explain this method, let us describe the distribution of the desired function v(x, y) along some straight line l with the parameterization (2)(2) –(3)(3) . Using this parameterization, we shall define the function v(x, y) for x,y∈ l as functions v(t) of variable t. We consider the domain Ω as a unit circle and define parameters t0,t1 that correspond to the points of the intersection of line l and boundary Γ.

The Local Ray Property (LRP) of the potential for any stationary electric field obtained by the author in [6] considers the family of ordinary differential equations (17) depending on ϕ,p, as the local analogs of the Laplace equation (15)(15) . The boundary condition (16)(16) leads to the following local boundary conditions (18) where Jn(xi,yi) corresponds to the values of the boundary function in (16)(16) , calculated in the boundary points (--18) i=0,1.

If we define (--19) as the solution of the local problem (17)(17) –(18)(18) , then we can formulate the LRP as the adequate local description of the potential v(x, y) on any straight line (ray) by the function (--20) , so that the final formula is true (19) where R⁻¹ is the inverse Radon transform operator.

For the solution of the Neumann boundary problem (15)(15) –(16)(16) we have obtained the next formula from LRP: (20) In [6] a similar formula based on the LRP was obtained for the solution of the Dirichlet boundary problem.

Formula (20)(20) presents the new explicit method for the solution of boundary value problems for the Laplace equation. The proposed formulae do not require solving any equations, because the Radon transform can be inversed by explicit formulae. Thus, the algorithm constructed by author and the corresponding computer software, which realizes proposed method, are sufficiently fast. This has been demonstrated in [6] for the Dirichlet problem by some numerical experiments, particularly in comparing with the PDE toolbox of the MATLAB system. We present here one model example in figure 1, which demonstrates the correctness of formula (20)(20) .

Figure 1. Solution of the Neumann boundary problem for v(x,y) = x+y, the number of discrete points n = 21, 41, 81.

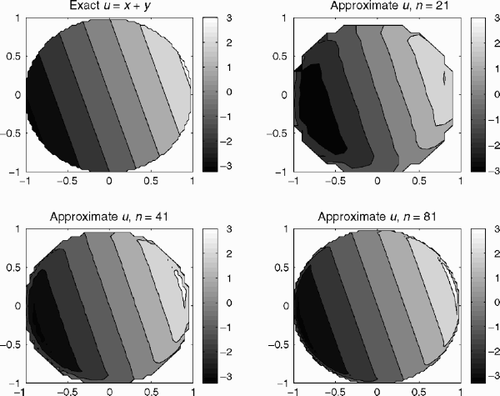
The LRP (19)(19) seems to be very important for physics, because it is the basis of the new explicit methods and fast algorithms for solution of physical problems described by the boundary problems for the elliptic equations. Some algorithms were constructed and justified numerically by the author in [7,8] for the solution of the Dirichlet boundary problem for the Laplace equation with an arbitrary simple connected star (not convex) domain Ω and continued boundary Γ

5. Regularization algorithm

It is simpler to justify, using properties of the Radon transform, that if the operator (--21) exists, it is the unbounded operator from L2 into L2, bounded from the Sobolev space (--22) into L2. This defines the character of the instability at solving the equation (14)(14) , which is equivalent to the instability of the problem of differentiation. In [9,10] a linear fast regularization algorithm was proposed, theoretically and numerically justified for the class of the unstable problems of this type. In our case this algorithm includes the recursive smoothing (RS) for stable calculation of the operator (--23) (derivatives (--24) ), and it also includes the application of RS for the input data, if they are noised. It then guarantees the stable (numerical) inversion of the operator (--25) on the smoothed right-hand side of the considered equation. Recursive smoothing is based on the explicit formulae for two-dimensional splines, constructed on the regular uniform net. We suppose for simplicity of explication that only the function u⁰(x,y,ϕ) in Dirichlet boundary conditions is not sufficiently smooth because it is noised. Hence, we have the same property for the function ν (p,ϕ) in the equation (14)(14) . Let this function be given in the nodes pi,ϕj of the uniform rectangular net on Ω0=p∈[−1,1],ϕ∈[−π/2,π/2], pi=−1+h1(i−1), h1=2/(n−1);ϕj=−π/2,+ h2(j−1), h2=π/(n−1); i,j= 1,…, n. Let si(u) be a local basic cubic spline, constructed on the units ui−2,…, ui+2; i=0,…, n+1; where u is p, or u is ϕ auxiliaries nodes for i⟨ 1,i⟩ n are uniforms. We use the formulae of the recursive smoothing spline algorithm [10,11], for the case of function of two variables: (21) (22) The number of smooths (--26) is the regularization parameter that can be chosen in accordance with the residual principle [12]. Recursive smoothing spline algorithm together with G-method give us the linear regularization algorithm for computer tomography.

6. Numerical experiments

Although the theoretical foundation of the existence of operator (--27) is under investigation, we shall present a model example to demonstrate the authenticity of penetrating tomography and the possibility of application of regularized G-method. Let the domain Ω be a circle of radius r=0.5, permittivity ϵ (x,y)= 1/cos (x+y). The external electromagnetic stationary field produces in Ω potential u(x,y)=sin (x+y), so that (--28) The exact function ν (p,ϕ)= sin (x¹+y¹)−sin (x⁰+y⁰), xⁱ= pcosϕ −tisinϕ, yⁱ=psinϕ +tⁱcosϕ, ti=(−1)ⁱt, (--29) is finally calculated using the formula (-3) Since (--30) , the operator (--31) has the explicit inverse and the function γ (x,y)=1/ϵ (x,y) is defined by the formula (23) where R⁻¹ is the inverse Radon transform. We calculate recuperation (--32) using the formula (23)(23) with the approximate inverse Radon transform realized as a computer program iradon in MATLAB system. We use the discreet values of the exact function ν and noised function (--33) where δ (p,ϕ) is the randomized function with estimation |δ|C,[Ω]<δ0. We apply the above described recursive smoothing to the noised function (--34) which guarantees the regularization property of the algorithm in a hole.

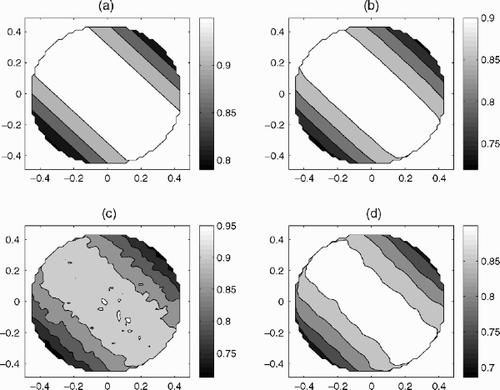
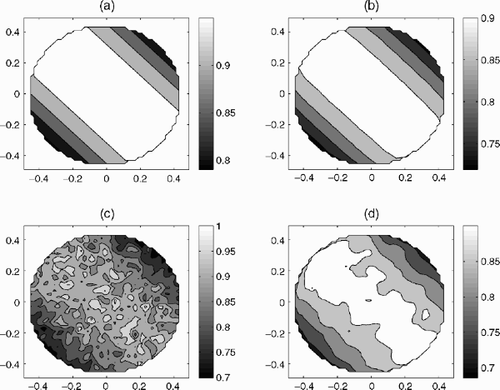
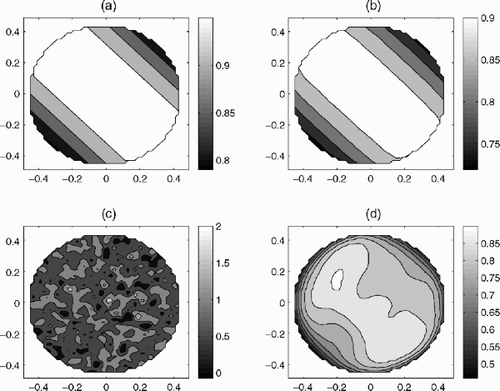
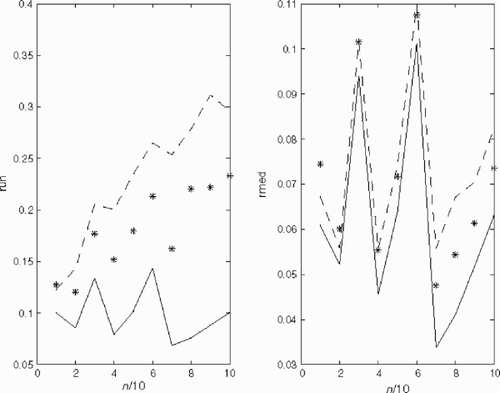
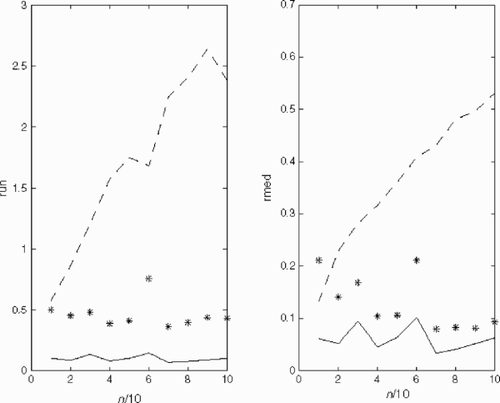
The results of numerical experiments on reconstruction γ (x,y) by (23)(23) for discretization parameter (number of nodes of the uniform red) n=51, estimations δ0=0.01, δ0=0.03,δ0=0.3 are presented in figures 2–4 correspondingly: graph (a) – exact γ (x,y)=cos (x+y); graph (b) – reconstruction with exact ν; graph (c) – reconstruction with noised (--35) without regularization; graph (d) – reconstruction with noised (--36) by proposed regularization algorithm.

Figure 2. Reconstruction of the electrical penetrating tomography image for δ0=0.01.

Figure 3. Reconstruction of the electrical penetrating tomography image for δ0=0.03.

Figure 4. Reconstruction of the electrical penetrating tomography image for δ0=0.3.

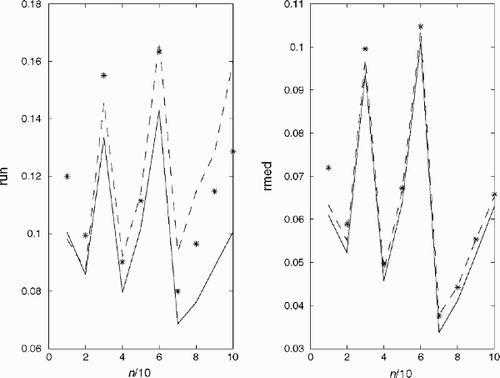
To characterize the quality of the algorithm in more detail, we use the discreet estimations of the accuracy of reconstruction of the function γ (x,y) in the nodes of uniform red xi,yj that lies inside the circle Ω. The estimation in uniform norm is calculated by the formula (-4) and the averaged estimation is defined by the relation (-5)

In figures 5–7 the functions run(n) (a) and rmed(n) (b) are represented correspondingly: the solid line – for exact ν (p,ϕ); the dashed line – for noised (--37) without smoothing; stars – estimation of reconstruction with noised (--38) by proposed regularization algorithm. Figures 5–7 correspond to δ0=0.03, δ0=0.1,δ0=0.3 accordingly.

Figure 5. Estimation of the accuracy of reconstruction for δ0=0.03.

Figure 6. Estimation of the accuracy of reconstruction for δ0=0.1.

Figure 7. Estimation of the accuracy of reconstruction for δ0=0.3.

7. Conclusions

The results and other numerical experiments presented, realized by the author, confirm the consistency of the proposed approach and the good property of the constructed algorithms. Some previous results on regularization algorithms for scanning computer tomography are described in [4,13].

Additional information

Notes on contributors

Alexandre Grebennikov *

Email: [email protected]

Notes

Email: [email protected]