Abstract
We consider the plane statement of Inverse Electroencephalography Problem (IEP), which consists in reconstruction of the electric potential distribution in the head and current distribution on the brain boundary using the electroencephalographic measurements on the scalp. The model of the human head is represented here by two homogeneous electric conducting parts with distinct conductivities, one inside the other. The inner part corresponds to the brain which is bounded by the curve S1. The second part corresponds to the rest of the head that goes from S1 to the scalp boundary S2. The investigation of the stability of IEP considered here consists in comparing solutions of the IEP as a boundary problem for the Laplace equation for two different geometric models of the brain curve S1 with the same model of the scalp curve S2. Two models are considered: (1) basic model, when (--1) and S2 are concentric circles; (2) perturbed model, when S2 is the same circle, but the curve
(--2) of brain boundary differs from
(--3) on oscillating function, bounded in the uniform norm with the known small parameter ϵ (that corresponds more to the real brain boundary, than circle). On the base of the potential theory and the Fourier series technique the existence and uniqueness of the solutions for both the models are justified. The stability result for the potential and the uniform norm estimation are obtained. These theoretical model results are used to the real values of the geometric characteristics of the human head, which appears in the classic investigations of Nuñez. Obtained results are important for the traditional Electroencephalography (EEG), which realize analysis in the frame of the basic model with two concentric circles, and also are perspective for the mathematical and engineering modelling in EEG.
1. Form of the model and statement of the problem
The model taken here is suggested in Citation[1–Citation5] and used also in Citation[6–Citation8]. Electric potential u1 inside the brain (region Ω1), which boundary will be represented by the curve S1, and electric potential u2 in the region Ω2 between brain and scalp, of which the external boundary is the curve S2, are solutions of the Laplace equation
(1)
These solutions must satisfy the following boundary conditions:
(2)
(3)
(4)
where [ui]Sj means the values of the function ui on the boundary Sj, function Vmed represents values of the measured potential u2 on the boundary S2. We determine the potentials u1 and u2 in the regions Ω1 and Ω2 as superposition of the potentials created by the electric charges with unknown densities μ1(y) and μ2(y), parametrized with the variable y, distributed on S1 and S2 correspondingly. We shall employ the simple layer potential theory Citation[9,Citation10] and present ui,i=1,2 in the following way:
(5)
We shall investigate the stability of the exact solutions
(--4) , i = 1, 2, constructed for concentric circles, considering the approximate solution
(--5) , obtained for a perturbed model, in the sense of the following:
Definition The solutions (--6) of the boundary problem is said to be stable if
(6)
where ϵ is a small parameter associated with the perturbation.
2. Basic geometric model: concentric circles
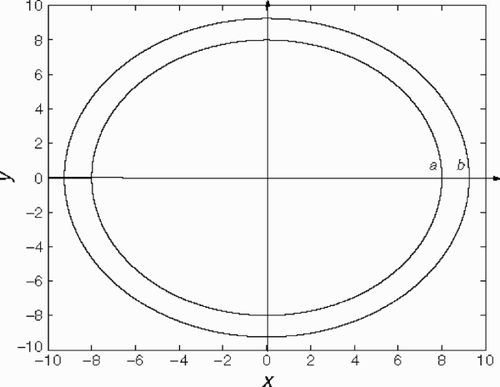
In this case, the regions Ω1 and Ω2 are defined by means of two concentric circumferences of radii a and b where a < b (). These circumferences will be represented in the following way: | y| =a and |y|=b. Region Ω1 is the interior of the circle of which the boundary is the circumference | y| =a. Region Ω2 is the interior of the set of points located between both circumferences.
The boundary conditions
(-1)
can be reexpressed using Equation(5)
(5) in the next form
(7)
(8)
where y1 represents any point of the circumference | y| =a, y2 and x are any points of the circumference | y|=b. We use polar coordinates (r,ϕ), for x and (r,θ) for the points y1 and y2 in these coordinates the points will be indicated by relations
(9)
(10)
We consider below the simplified normalized model form for the measured potential as the following:
(11)
where m is a positive integer. In terms of complex exponentials
(12)
THEOREM 1 The boundary problem Equation(7)(7) –Equation(8)
(8) for Vmed=sin mϕ, m a positive integer, has a unique solution given by
(13)
(14)
Proof Using Equation(9)(9) and Equation(10)
(10) in Equationequations (7)
(7) and Equation(8)
(8) and representing μ1(θ), μ2(θ) and Vmed(ϕ) by series of Fourier Citation[11]:
(15)
we arrive at equations:
(16)
(17)
where
(-2)
Substituing the integrals given in Equation(16)
(16) and Equation(17)
(17) for its values and using formula Equation(12)
(12) we obtain
(18)
(19)
Remembering that the system of exponentials:
(-3)
is orthonormal and complete we can deduce from Equation(18)
(18) and Equation(19)
(19) the following sets of equations:
(20)
(21)
(22)
(23)
Solving these systems we find constants distinct from zero:
(24)
Substituting the constants in Equation(24)
(24) into formulas given by Equation(15)
(15) we obtain
(25)
(26)
Substituting Equation(25)
(25) and Equation(26)
(26) in Equation(5)
(5) and integrating, we have the final formulas Equation(13)
(13) and Equation(14)
(14) that finishes our proof.▪
3. Perturbed model: curve  and circumference S2
and circumference S2
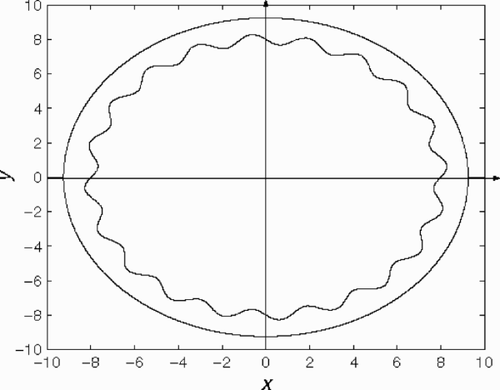
We now suppose that the inside curve (--8) is the set of points y1 defined by equation:
(27)
and that the external curve S2 is the circumference | y|=b. Both curves are concentric (see ). They are used below for a = 8, b = 9.25, n = 20 and ϵ = 0.3.
We utilize again formula Equation(5)(5) changing in them | y| =a by the curve
(--9) . In this case we shall use a first-order approximation on ϵ in the integrands where it appears. After this we follow the same steps as in the above case. We suppose once more that
(-4)
The following result takes place.
THEOREM 2 The boundary problem Equation(1)(1) –Equation(4)
(4) for a perturbed model has a unique solution and its first-order approximation on ϵ is given for Vmed(ϕ)=sin mϕ, by formulas:
(28)
(29)
Proof For this case, existence and uniqueness of the exact solution of the problem Equation(1)(1) –Equation(4)
(4) follows from known results for the Cauchy problem for the Laplace equation Citation[10]. We present the proof for the case n>m, for the cases m = n and n < m the proof is similar. Approximate solutions of the system of the 12 equations, which appears from boundary conditions in the first-order approximation on ϵ, are the following:
(-5)
(-6)
Using these constants we obtain approximately the charge densities:
(-7)
After substituting these densities into Equation(5)
(5) we obtain the desired formulas Equation(28)
(28) and Equation(29)
(29) , that obviously satisfies the Laplace equation and the three approximate boundary conditions.▪
THEOREM 3 The exact solutions for the basic model are stable according to Definition Equation(6)(6) for pertubations Equation(27)
(27) and the approximate solution given by Equation(28)
(28) and Equation(29)
(29) .
Proof In accordance to formula Equation(28)(28) we obviously have the relation
(-8)
From Equation(14)
(14) and Equation(29)
(29) it follows that
(--10) . So, we conclude the stability of the solutions.▪
Now we compare the potentials on the brain for both geometrical models:
(-9)
If we take
(--11) as the approximate value and
(--12) as the exact value, then the relative error for
(--13) is given by formula:
(30)
The relative error is small if values of m are not too great. For instance, from Citation[3] we have the following data for a lot of models of real brains: n = 50, ϵ = 0.365 cm, a = 8 cm and b=9.25 cm. The relative error is less than 0.1 for 1<m<4.
4. Conclusions
On the base of the potential theory and the Fourier series technique the existence and uniqueness of the solutions of IEP for two considered models are justified. The stability result for the potential in the uniform norm estimation is obtained and confirmed by calculations with the real values of the geometric characteristics of the human head. Obtained results are important and perspective for the mathematical and engineering modelling in EEG.
Acknowledgments
The research was supported in parts by the VIEP BUAP No II 105-04/EXC/G project.
- Plonsey, R, 1969. Bioelectrical Phenomena. New York. 1969.
- Koptelov, Yu.M, and Zakharov, EV, 1992. Ill-posed Problems in Natural Sciences. Moscow. 1992. p. pp. 543–552, In: A. Tikhonov (Ed.).
- Nuñez, PL, 1981. Electric Fields of the Brain. New York. 1981. p. pp. 1–11.
- Amir, A, 1994. Uniqueness of the generators of brain evoked potential maps, IEEE Transactions on Biomedical Engineering 41 (1994), pp. 11–23.
- Sarvas, J, 1987. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem, Physics in Medicine and Biology 32 (1) (1987), pp. 11–22.
- Solís, SSergio, 2000. "Problema inverso electroencefalográfico para el caso de dos esferas no concéntricas". In: Tesis de Maestría en la BUAP, México. 2000.
- Fraguela, CAndrés, Grebénnikov, AI, and Solís, SS, 2000. "Analysis of one electroencephalography inverse problem for the human head model as two nonconcentric spheres using spherical harmonics". 2000, Paper presented at the international conference: Inverse and Ill-posed Problems, Moscow.
- Fraguela, A, Grebénnikov, AI, and Solís, SS, 2001. "An inverse problem of electroencephalography for a model of human brain activity. In: V.A. Sadovnichii and E. Doger Guerrero (Eds)". In: Mathematical Modeling of Complex Information Processing Systems. Moscow. 2001. p. pp. 144–146.
- Tijonov, AN, and Samarsky, AA, 1980. Ecuaciones de la Física Matemática. Moscow. 1980.
- Vladimirov, VS, 1971. Equations of Mathematical Physics. New York. 1971.
- Arfken, G, 1970. Mathematical Methods for Physicists. Moscow. 1970.