Numerical solution of 3D unsteady nonlinear inverse problem of estimating surface heat flux for cylindrical geometry

Abstract

A numerical algorithm is proposed for solving a three-dimensional unsteady nonlinear inverse heat conduction problem of estimating the boundary conditions at the heated surface of a solid. In this study, the geometrical form of the solid is a finite hollow half-cylinder. As additional information, needed to solve the inverse problem under study, we use both temperature measurements at the internal surface (case of the use of thermo-couples or an infrared camera) inside the half-cylinder (case of the use of thermo-couples) and those at the heated surface (case of the use of an infrared camera). The iterative regularization method is used to build the numerical algorithm. The method is based on the residual functional minimization by using the unconstrained conjugate gradient method with the regularizing discrepancy principle as a stopping criterion of the iterative processes. The unknown function of three variables is sought for as a grid function.

Keywords:

• 3D unsteady nonlinear inverse problem
• Cylindrical geometry
• Iterative regularization method

1. Introduction

Linear and nonlinear inverse heat conduction problems have been analyzed very intensively during the last 35 years or so. There are excellent books on this subject [1–4]. For two-dimensional linear and nonlinear inverse problems a great progress has been achieved in the last decade [5–10]. It should be noted that two-dimensional (2D) heat conduction problems have been much more extensively investigated than 3D inverse problems. Indeed, the solution of 3D nonlinear inverse problems is very time-consuming and requires a large random access memory. This is one of the main reasons why just a few works are published in this promising direction of inverse problems up to date. The last developed studies were performed by Alifanov and Nenarokomov [11], Huang and Wang [12], Huang and Chen [13], Nortershauser and Millan [14], and Dowding and Beck [9].

The main goal of this work is to develop a numerical method and computational tools for solving a 3D unsteady nonlinear inverse heat conduction problem of estimating the boundary conditions at the heated surface of a hollow half-cylinder. The inverse heat conduction problems are ill-posed, which leads to a large sensitivity of the obtained numerical solution to measurement errors. That is why a regularization is needed to stabilize numerical solutions. We use the iterative regularization method to build the numerical algorithm and to stabilize the inverse problem solution.

The geometrical form of the analyzed solid is a finite hollow half-cylinder. The inverse problem is to estimate a heat flux density evolution at the external surface. Three computational situations are analyzed which are connected with a possible scheme of temperature measurements. In the first case, measurements are simulated numerically at the internal surface of the half-cylinder (case of the use of thermo-couples). In the second case, temperature measurements can be realized inside of the solid (with thermo-couples). The last situation deals with the temperature simulation at the external heated surface (case of the use of an infrared camera).

The performance and the error analysis of the inverse heat conduction problem solutions obtained by the proposed algorithm are analyzed by considering several heat flux test cases in function of space and time. Indeed, a nonlinear 3D analysis was conducted to analyze the performance of the iterative regularization method and its capability for experimental data processing.

2. Inverse problem

The geometry of a solid considered in this article consists of finite hollow half-cylinder with inside radius r0, outside radius r1, and length z1, as illustrated in figure 1. The lateral surface of the half-cylinder is submitted to an unknown heat flux while all other boundaries are kept insulated. The nonlinear heat conduction process in cylindrical coordinate system, i.e. T(r,ϕ,z,t), is described by the following set of equations: (1) (2) (3) (4) (5) (6) When the applied heat flux density q(ϕ,z,t) is known, the presented model (direct problem) is used to predict temperature field. When the applied heat flux density q(ϕ,z,t) is unknown, but an additional information in the form of temperature measurements is available, the previous problem can be solved to estimate both temperature distribution and applied heat flux density by solving the inverse heat conduction problem.

Figure 1. Geometry model and boundary conditions.

In this work, we suppose that temperature measurements are carried out at a cylindrical surface with radius d which represents a parameter determining the position of measurement surfaces, with respect to the external and internal radii, r0≤ d≤ r1. In this case, the measurement results can be presented as follows: (7) Besides that, the number of discrete measurement points at a measurement surface is big enough so that the function f(ϕ,z,t) can be presented as a piece-wise linear continuous function. The inverse problem under analysis is to estimate the heat flux density q(ϕ,z,t) by using the direct problem (1)(1) to (6)(6) and the temperature measurements (7)(7) .

3. Algorithm

The iterative regularization method is used to build a numerical algorithm of the above inverse problem. The method is based on a variational formulation of an inverse problem. First, that leads to the introduction of the residual functional which determines the ‘distance’ between the response of the system computed by solving the direct problem according to the measurement scheme and the measured response. In the majority of practical applications the residual functional (the distance between two responses) is defined in the Hilbert space L2 of square integrable functions. For the inverse problem analyzed in this article we use the continuous form of the residual functional. It is defined as (8) where δ (ϕ,z,t) represents the distance T(d,ϕ,z,t;q) −f (ϕ,z,t), T(d,ϕ,z,t) designates the temperature evolution computed at the measurement surface S(d,ϕ,z) and f(ϕ,z,t) represents the measured temperature evolution at the same surface respectively.

Second, it is necessary to define what kind of function is sought for. That is, a space to which the unknown function belongs should be specified. In our inverse problem the desired function is sought for as grid function and is considered as an element of the Hilbert space L2.

Third, it has been shown for linear general inverse problems (in operator form) [1,15] that one of the very effective approach to obtain a stable solution of inverse problems is to use unconstrained, on the desired function, gradient-type numerical methods of the first kind for the problem of the residual functional minimization given by (9) under constraints on the temperature given by all equations of the direct problem (1)(1) to (6)(6) , because the temperature in the specimen cannot be fixed arbitrarily. It is computed from the direct problem.

The most efficient gradient-type numerical method is the conjugate gradient method [16]. The successive improvements of the desired function are built as follows (10) where s is the iteration number, γ^s is the descent parameter, and D^s(ϕ,z,t) is the descent direction, and q⁰(ϕ,z,t) is an initial approximation of the unknown function given a priori. The descent direction is given by: (11) where the parameter β^s is given by formula (12)(12) when using Polak–Ribire version i.e. (12) where (--1) , or expression (13)(13) when using Fletcher–Reeves version of the conjugate gradient method [16]: (13) In the absence of measurement noise (this is a typical case for optimal control problems), numerical experiments show that the above iterative process can be repeated until the function q(ϕ,z,t) satisfies the following stopping criterion: (14) where ϵ is a small number (10⁻⁴ to 10⁻⁵). This property of the conjugate method is very useful. It is widely used to verify numerical algorithms and programs for solving test inverse problems without noise.

As it is well known, inverse problems of experimental data processing cannot be solved as easily as direct problems because of their inherent ill-posed character. Indeed, their solutions do not depend continuously on the data. Small changes in the input data can produce large deviations in the solution [1,2,17]. The iterative regularization method [1,11] is used to stabilize the solution of the studied inverse problem. The idea of the method is based on the use the discrepancy principle as a stopping criterion for the iterative process: (15) where δ² is the generalized measurement error computed at the same space as the residual functional (16) σ (ϕ,z,t) is the standard deviation of measured temperatures obtained using smoothing techniques for example. In other words, this approach is the regularization method and gives regularizing algorithms. It is possible to give a simplified explanation of the general idea of the iterative regularization method. To do that, consider an inverse problem as the equation (17) where Tc(q), for a given q, is the solution of the direct problem which corresponds to the measurement scheme. Suppose that Tcomp(q) is calculated more or less exactly as what is determined by a numerical approximation of the direct problem, and the measured response f is known exactly. In such a case, we have an optimal control problem and an (approximately) exact solution q is obtained by using the conjugate gradient method. To keep this ‘good’ solution introduce a noise ε, we obtain: (18) The approximately exact solution is kept. Then, one can write (19) Equation (19)(19) is exactly the discrepancy principle in which the solution of this equation is close to the exact one. So, it is necessary to solve the equation (19)(19) to have a good and stable solution of an inverse problem. The central question is how to solve this equation?

The main theoretical result which gives the iterative regularization method is that it is possible to solve approximately equation (19)(19) by applying the gradient-type numerical method of optimization, in particular the conjugate gradient method, and using the regularizing discrepancy principle as a stopping criterion to obtain the stable solution close to the exact one. The rigorous mathematical analysis of the method for linear inverse problems and some of its applications are given in [15].

The minimization of the residual functional (8)(8) by the conjugate gradient method requires the computation of its gradient with respect to the desired function q(ϕ,z,t) in the space L2. There are several ways to derive the gradient of J(q). One way is to use the calculus of variations and Lagrange multipliers method [15]. A similar approach has been used in reference [10]. Finally, all methods lead to the adjoint problem which is used to compute the residual functional gradient. The same approach is applied in this article. It can be shown that the residual functional gradient in the space L2 is given by: (20) where ψ (r1,ϕ,z,t) is solution of the ‘adjoint problem’ given by the following set of equations: (21) (22) (23) (24) (25) (26) (27) The descent parameter γ^s, which characterizes the step size in going from q^s to q^s+1, is obtained at each iteration by minimizing J(q^s+1) given by equation (8)(8) , with respect to γ^s. For our inverse problem the following result is obtained: (28) In the above formula, υ (r,ϕ,z,t) is solution of the ‘variation problem’ defined by the following system of equations (29) (30) (31) (32) (33) (34) T(r,ϕ,z,t) is the solution of the ‘direct problem’ given in equations (1)(1) –(4)(4) , and f(ϕ,z,t) is the measured temperature at the surface defined by r =d, 0≤ ϕ ≤ π, and 0≤ z≤ z1. In the variation problem, the term Δ q(ϕ,z,t) is defined by Δ q(ϕ,z,t) =  D^s(ϕ,z,t), the descent direction.

4. Minimization procedure

The minimization procedure can be implemented following this scheme:

1.	Give an initial guess for q0.
2.	Solve the direct problem given in equations (1)(1) –(4)(4) .
3.	Solve the adjoint problem represented by equations (21)(21) –(27)(27) .
4.	Compute the gradient function expressed by equation (20)(20) .
5.	Compute the descent direction as given by equation (11)(11) .
6.	Solve the variation problem expressed by equations (29)(29) –(34)(34) .
7.	Compute the descent parameter represented by equation (28)(28) .
8.	Increment the vector q following equation (10)(10) .
9.	Check convergence using formula (14)(14) or (15)(15) . Otherwise go to step 2.

At each iteration, we must solve three problems, the ‘direct,’ the ‘adjoint,’ and the ‘variation’ problems. As these problems are similar, we can use the same algorithm to solve them numerically. These problems are solved numerically using the control volume method [18] and the implicit fractional-step time scheme proposed by Brian [19,20]. This scheme is given by: (35) where (--2) , (--3) , and (--4) are the second finite difference operators in r, ϕ, and z directions. By using this scheme only a three-diagonal matrix inversion is carried out with the Thomas algorithm [20] (TDMA).

5. Results

To illustrate the application of the iterative regularization method for 3D transient nonlinear inverse problem, we consider several examples of estimating numerically the time and space-wise variation of an applied heat flux from the knowledge of transient temperature recordings taken at the measurement surface S(d,ϕ,z). Three different cases are considered. The first example uses temperature field measured on the back side of the half cylinder where the distance d is given by d = r0. In the second test temperature measurements are collected somewhere between the external and internal surfaces characterized by the distance r0 < d < r1. The last example uses the temperature measurements taken over the external surface, i.e. d=r1, which correspond to the first motivation of this study [21–23]. A Delta Fourier number, ΔFo (dimensionless time step), based on the sensor depth ϱ, the thermal diffusivity α, and the time step Δ t is introduced to characterize the difficulty degree of the analyzed inverse heat conduction problem. It is defined as: (36) The analyzed test cases give different values in the same range as those presented in the literature [1,2] i.e. (--5) [. The geometric characteristics and thermophysical properties of the model are given by (-1) The spatial and temporal resolution is taken to be nr × nϕ × nz × nt =21 × 21 × 21 × 201. The measured temperatures are simulated by the following expression (37) where Tx(r1,ϕ,z,t) is the exact temperature over the external surface. In fact to the theoretical temperature profile Tx(r1,ϕ,z,t) we add a white and normal noise. The perturbation is defined as ω Tmax Δmax where ω is random number generator [ −1, +1], Tmax is the maximum temperature value over the heated surface, and Δmax is the magnitude of the perturbation (in %). In the following numerical tests the parameter Δmax is taken to be equal 2%. The stopping criteria in these cases is based on the iterative regularization method, equation (15)(15) . The iterative process (equation (10)(10) ) is stopped when the value of the functional residual reaches approximately the δ ² value (see equation (15)(15) ).

The presentation of the results in three dimensions (ϕ,z,t), could be confusing and difficult to understand. This is the reason why in this study we present our numerical simulations in two dimensions (ϕ,t). To do that we can consider that the heat flux presents the same variation following ϕ or z. Finally, the estimation error of the desired function q(ϕ,z,t) is computed according to the formula: (38) where (--6) and q(ϕ,z,t) are respectively the exact and recovered functions. All of the presented test cases were performed with exact (errorless) and noised data. The computation results with errorless data are not presented here since the recovered results reveal almost no difference from the original (exact profile) applied heat flux density.

Test case 1 We have chosen a sinusoidal variation over time for the heat flux in the first example. The final time is taken as tf = 100 s. The heat flux is supposed to be constant over ϕ and z (no variation). The temperature measurements are supposed to be collected over the internal surface of the half cylinder, i.e. d=r0 which results in Δ Fo = 0.028. With regard to the literature [1,2,15], this case represents a very difficult example due to the amplification of the errors when solving the problem. 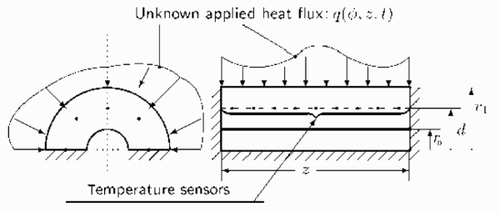The unknown transient heat flux over the surface S(d,ϕ,z) is assumed to vary as: (39) The maximum of heat flux density (qm) in this case is about 75,000 W m⁻². The first step was to show the robustness of the developed algorithm, we present in figure 2 the different results obtained. The shown results underline the capabilities of the algorithm to overcome the difficulties due to the used noisy data. As presented in figure 2(d), the difference between exact values and computed values of the heat flux density at the point p located at (r=r1, ϕ = π /4, z=z1/4). This difference is still reasonable even around the maximum points where the heat flux undergoes the biggest change. The presented results were obtained in 25 iterations with a CPU time of 233 s. The estimation error is 3.87% according to expression (38)(38) . By analyzing the two profiles presented in figures 2(a) and 2(b), it confirms the excellent agreement between the estimated and the exact heat flux shapes. Figure 2(c) shows a plot of the difference between exact and recomputed heat flux density values when we use noised temperatures in this first test case. Inspecting figures 2(a), 2(b), and 2(c)s, we observe that the error of estimated time function is still small in comparison with the added noise. From the presented case we conclude that reliable inverse can still be obtained when measurements errors are considered.

Figure 2. Numerical results for test case 1 obtained with Δ Fo = 0.028. (a) Recovered heat flux density distribution; (b) exact heat flux density distribution; (c) difference between exact and recovered heat flux; and (d) heat flux profile at the point p.

Test case 2  The developed algorithm was tested for a second example. In this case the measurement is supposed to be taken at a distance d, from the active surface, located in the middle between the external and internal surfaces of the half-cylinder i.e. r0 < d = (r1 + r0)/2 < r1. The final time is chosen as tf=100 s. The corresponding Δ Fo = 0.11 which implies an easier test case than the first one. 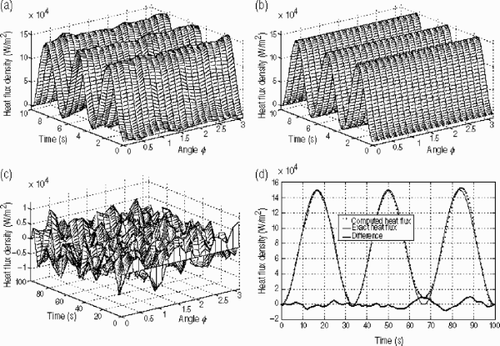The transient heat flux density to be retrieved is supposed to vary as: (40) In this case the maximum heat flux is chosen as qm=7.5 × 10⁸ Wm⁻². The second example supposes that there is spatial variation following ϕ. Figure 3 summarizes the recovered results when we use noised data with a maximum amplitude of 2%. The shown results were obtained in 24 iterations with a CPU time of 224 s. The estimated heat flux density, figure 3(a), presents a small roughness at its basis but still stable with respect to the input data. The obtained results confirm the efficiency of the developed algorithm. The difference between the exact and recovered heat flux density values for this case are presented in figure 3(b). The residuals are of the same order of magnitude than those observed in the first example even though there is a big difference in temperature maximum reached in both cases. The second case presents the highest maximum temperature. The estimation error is 6.35% according to expression (38)(38) which is a little bit high due to the weak space modeling (nr × nϕ × nz) of the heat flux density. In fact, a greater space resolution would be better to represent correctly the space variation.

Figure 3. Numerical results for test case 2 obtained with Δ Fo = 0.11. (a) Recovered heat flux density distribution; (b) exact heat flux density distribution; (c) difference between exact and recovered heat flux; and (d) heat flux profile at the point p.

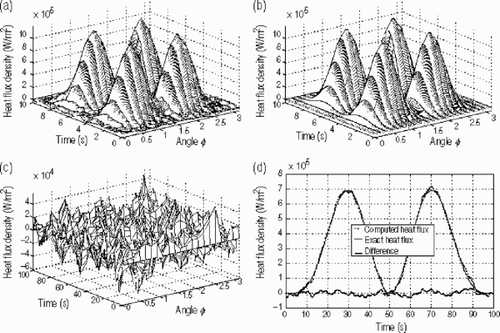
The time variation of the heat flux density at the point p, located at (r=r1, ϕ = π /4, z=z1/4), is plotted in figure 3(d). The comparison between the exact and recovered heat flux profiles shows an acceptable agreement and the estimated heat flux becomes more close to the exact one. The estimated results show a small roughness in comparison with those presented in the first test case. This roughness is probably due to the space variation of the heat flux and to its poor space step number in the angle direction (ϕ). The same figure presents also the difference between theoretical and estimated heat flux density profile, at the point p, for the second case when using noisy data. Regarding the displayed residuals, figures 3(c) and 3(d) the recovered results are more accurate than those observed in the first case which is consistent with the physics of the problem. In other words, as the temperature measurements are taken at a distance closer to the active surface than the first example, the estimation is better. The two test cases presented previously verify the application and the accuracy of the method when the measurements are taken inside the body.

Figure 4. Numerical results for test case 3 obtained with Δ Fo → ∞. (a) Recovered heat flux density distribution; (b) exact heat flux density distribution; (c) difference between exact and recovered heat flux; and (d) heat flux profile at the point p.

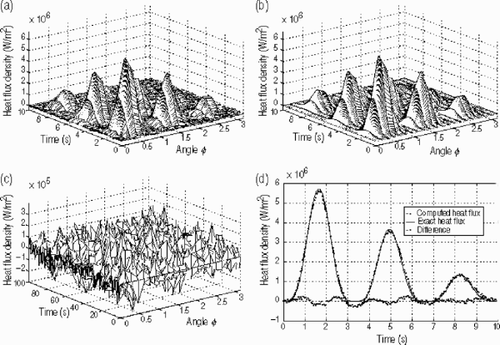
Test case 3 In this paragraph, the developed algorithm will be applied to a situation where the temperature measurements are collected on the same surface where the unknown is sought for (where the unknown heat flux density is acting) (see figure 1). This configuration gives Δ Fo → ∞ which results in a weakly ill-posed problem or a pseudo-inverse problem [1].

To show the application of 3D inverse heat conduction algorithm we present a third test case. This example consists in recovering the space and time variation of the heat flux density expressed by (41) In this case the maximum heat flux is chosen as qm=7.5 × 10⁶ W m⁻². The final time for the numerical experiment is taken as tf = 10 s. The example consists in sinusoidal variation following ϕ and t with variable amplitude. The recovered time and angular evolution is presented in figure 4(a). The exact heat flux density is displayed in figure 4(b). This estimation is performed with noised data with the same amplitude of 2% of the maximum surface temperature. The shown results are obtained within 73 s of CPU time and with an error of 15%. Here again, the relatively huge error is due to the poor space discretization rather than the estimation procedure.

The recovered heat flux at the point p located at (r=r1, ϕ = π /4, z=z1/4) is presented in figure 4(d). The computed surface heat flux fits the exact heat flux profile in a satisfactory way. The difference between the recovered and exact heat flux density profile at the point p is shown in the same figure 4(d). Here again the estimated results are acceptable and underline the efficiency of the developed iterative method.

In all the presented numerical simulations, no a priori information on the unknown evolution to be recovered was used and the initial guess of the heat flux density was taken all the time as null. Finally, the shown results were obtained with a Pentium 4, 2 GHz, with 256 RAM, under the Fortran Powerstation platform.

6. Conclusion

The objective of the present work was to show the application of conjugate gradient method coupled to the iterative regularization method for estimating 3D heat flux by using a nonlinear heat conduction model. This study was accomplished through the use of adjoint problem to compute the gradient combined with the conjugate gradient algorithm to minimize the residual functional. The algorithm was successfully implemented and relatively correct results were obtained with noisy measurements.

Three numerical simulations were performed to underline the robustness and stability of the developed method with different Delta Fourier number (Δ Fo). It was shown that the obtained results are still in the range of the desired estimation error. Further numerical verification tests shall be conducted to show the efficiency of this algorithm in the presence of high and low time and space frequencies in the heat flux density evolution. The parametric representation of the unknown also shall be used to address the relation between the number of parameters and the optimal number of measurements to perform an accurate estimation.

Nomenclature

Table

cp(T)	Specific heat, J kg^−1 K^−1
D(ϕ,z,t)	Descent direction
J(q)	Residual functional
J′(ϕ,z,t)	Residual functional gradient
k(T)	Thermal conductivity, W m^−1 K^−1
q(ϕ,z,t)	Unknown heat flux density, W m^−2
(--7)	Exact heat flux density, W m^−2
S(r0,ϕ,z)	Internal surface at r = r0
S(r1,ϕ,z)	External surface at r = r1
T(r,ϕ,z,t)	Temperature, K
Tx(r,ϕ,z,t)	Exact temperature, K
Ti	Initial temperature, K
t, tf	Time, final time, s
r,ϕ,z	Cylindrical coordinates, m, rad, m
Y(r,ϕ,z,t)	Measured temperature, K
β	Parameter in descent direction
Δ Fo	Dimensionless time step
Δ	Finite difference operator
δ	Integrated error
ϵ	Precision in iterating process
ε	Estimation error
γ	Descent parameter
ψ (r,ϕ,z,t)	Adjoint variable
ρ	Density, kg m^−3
υ (r,ϕ,z,t)	Temperature variation, K
σ (ϕ,z,t)	Standard deviation of measurement
n, n + 1	Time level
s	Iteration number