Abstract
We present a new numerical method to solve the inverse spectral problem for the fourth-order differential operator based on the identification of the Taylor coefficients of an analytic solution. We show that an analytic potential can be recovered from the knowledge of four spectra and prove that convergence follows from the exponential growth of the solution. The solution is obtained by a sequential algorithm by which four Taylor coefficients of the potential are recovered explicitly at each iteration.
1. Introduction
We would like to recover an analytic coefficient , where
from the spectral data of the regular differential equation
(1)
where h and k are complex parameters used to generate the different spectra. We use the simple fact that when q is analytic, the solution y(x,λ) of the initial value problem at x = 0 is a double-power series and the spectrum is obtained by solving boundary conditions at x = b in (1.1). In this work we show that reversing this procedure will produce a new and fast algorithm for the inverse spectral problem for the fourth-order case. Recall that although the classical Gelfand–Levitan theory has been extended to cover the general fourth-order case by McLaughlin Citation8,Citation9, its computational implementation remains extremely challenging. It is limited to the self-adjoint case and requires solving a continuous family of integral equations. Our work is close in spirit with the work by Freiling and Yurko Citation4, Theorem 4.5.1] and Citation12, on the inverse spectral method by the Weyl function. Although their algorithm requires few steps, it is not obvious how it can be implemented numerically as it requires computing the limit of the Weyl functions at infinity as λ→∞ while arg (λ)≠0. Also, working with the Weyl function presumes the knowledge of all its poles, the eigenvalues, and this we do not assume. In fact, our method approximates 4n Taylor coefficients of q from four sets of n eigenvalues each, that were obtained by varying h and k in (1.1). Convergence of the scheme is proved in the last section.
Because we use parameter identification, the method can handle the case when the eigenvalues are complex-valued, which is important in control theory Citation10. This work generalizes the method in Citation3 to the fourth-order case where two spectra are necessary; see Citation3 and Citation7. For our fourth-order problem (1) we shall need four spectra in order to recover the analytic coefficient q(x). A simple reason behind this is that the recurrence relation associated with the operator D4 moves by four terms at a time i.e. , where cn are the Taylor coefficients of the solution. We now outline the main steps of the method. In all that follows the function
is assumed to be analytic, with a domain of convergence that includes the interval [0,b], so the solution y(x,λ) of any initial value at x = 0 of the differential equation in (1.1) is also analytic in both variables x and λ,
Obviously the first question is how do the coefficients c(n,k) depend on the coefficients qk. Recursion relations allow us to express explicitly each c(n,k) in terms of qk, for example
The coefficients c(n,k), which are polynomials of the coefficients qk, can be stored as the entries of an infinite matrix. The next question is: given c(n,k) how can we recover the coefficients qk? A crucial fact and key to the method is to notice that in all c(n,k), the highest indexed term appears linearly, for example, q12 appears linearly in c(18,0), c(22,1), and c(26,2). It is this linearity that allows us to solve the inverse problem, in the sense that given the coefficients c(n,k), as we can isolate the highest qk. Another important fact is that c(18,0), c(22,1), and c(26,2) are parts of the same branch, as they contain the same monomials in qk. The first part of this work is to figure out how these polynomials in qk are generated so that we can write a code.
In the second part we show that by truncating this infinite system, we can generate a sequential algorithm, that explicitly gives four coefficients at each iteration. For example, in order to recover 80 coefficients qk, we need to solve sequentially 20 (4×4) explicit linear systems. This feature makes the algorithm very fast and very attractive from the computational viewpoint, as these systems are solved explicitly. Using the fact that y(x,λ) are of exponential growth, we prove that the truncation error tends to zero as we increase the size of the matrix and thus convergence of the scheme.
Recall that fourth-order differential equations, such as (1.1), have important applications in the design of beams and bridges, and where eigenvalues correspond to resonance Citation2,Citation4–8. It will be obvious at the end that because we are using a method of identification, the potential can be complex-valued and can be recovered from its complex eigenvalues. These are real situations which arise in control theory where it is required to find q(x) such that the corresponding eigenvalues are in the left half complex plane.
2. The direct problem
In this section, we present the spectral theory associated with the choice of boundary conditions of the differential equation (1.1), where h and k are real numbers. By choosing different values for h and k we can generate other spectra. The obvious advantage is that we use the same right boundary condition.
PROPOSITION 1
, the differential operator defined by (1.1) is self-adjoint and so the eigenvalues are real.
Proof
Let us denote by L the operator generated by the differential expression l
and defined on DL
We only need to show in other words
From Lagrange identity
where
Clearly is equivalent to
Using the fact that\;when f∈DL, we have
and from the first two boundary conditions, the above reduces to
or
Since f′′′(0), f′′(0), f′′′(b), and f′′(b) are arbitrary, we obtain
which means that g∈DL i.e.
Another method would be to express the boundary condition in a matrix form as
where
For the boundary conditions to generate a symmetric differential operator, we have to verify that
which is readily seen to hold since B1=Id and
.▪
We have mentioned that four spectra corresponding to different boundary conditions are required to solve the inverse problem. These spectra are generated by choosing different values of the parameters (h,k). We shall first investigate the associated initial value problem and obtain the main properties and estimates for the coefficients c(n,k). Only when the direct problem is studied, that the recovery process can be initiated.
2.1. The recurrence relation
Denote the general solution to the fourth-order differential equation
(2)
where
by
(3)
Since
and for a fixed k, by combining powers of x that add up to n,
leads to the recurrence relation
By matching the coefficients of (), we obtain the main recursion formula
(4)
and we agree to define c(n,-1)=0. From (2.2), the derivatives of yat x = 0 can be expressed as,
(5)
Because of the boundary conditions at x = 0 in (1.1), all solutions of (1.1) are combinations of two solutions ϕ and ψ defined respectively by the initial conditions
(6)
where
2.2. The solution 
If , then from (2.4) and the initial condition (2.5)
, one deduces that
(7)
Also, the conditions and
imply, respectively,
The condition on the other hand implies that
(8)
and so, using recursion formula (2.3), we can find the values of the remaining
, which can be represented as the entries of an infinite matrix c(n, k) as shown in and , where
The structure and properties of the entries c(n,k) are recorded in
Table 1. The first entries of the matrix c(n, k).
Table 2. The first entries of the matrix c(n, k).
PROPOSITION 2
The following identities hold for all k≥0:
| 1. | c(n,k)=0 0≤n≤4k+1. | ||||
| 2. | c(4k+2,k)=k!. | ||||
| 3. | c(4k+3,k)=c(4k+4,k)=c(4k+5,k)=0. | ||||
| 4. | c(4k+6,k)=-(k+1)!q0. | ||||
| 5. | c(4k+7,k)=-(2k+3) (k+1) !q1. | ||||
| 6. |
| ||||
| 7. |
| ||||
Proof
Observe that (2.3) is a double-recursion equation, namely on n and k. The first four columns of the matrix are already derived from the initial conditions and the simplest way is to use generating functions to prove most of the above points. Notice that entries c(4k+m,k) means starting at the position (m,0) and then moving k steps down and 4k steps to the right. This unveils the structure of the matrix c(n,k).
| 1. | The first point is certainly true for k = 0 since c(0,0)=c(1,0)=0. If we assume it true for k − 1 i.e. | ||||
| 2. | Observe that c(2,0)=1 was already given by (2.7), and (2.9) reduces to
| ||||
| 3. | For k = 0, it is obvious that c(3,0)=0 and again from (2.9) we deduce that
| ||||
| 4. | It is clear that c(6,0)=-q0 and (2.9) yields
| ||||
LEMMA 1
If a sequence satisfies for k=1,2,… then,
(12)
We only need to use the method of generating functions to obtain the coefficients ak. Let us denote by
and assume that the power series has a nonzero radius of convergence. The above recursion (2.11) yields
which means
Compare the coefficients
to obtain
From (2.10), we have a0= -q0 and b=q0 which implies and so
(5) Here we recall that and from (2.9) we obtain
Using the generating functions on the above recurrence relation yields
which proves this part.
(6) Similarly, we have
and again the generating functions method yields
(7) We already have and the recurrence relation (2.9) reduces to
from which follows that
The next section deals with the second solution.
2.3. The second solution
Express the second solution, which satisfies the initial condition by
Observe that the coefficients b(n,k) satisfy the same recurrence relation (2.3) but have different initial conditions, and hence we expect that b(n,k) and c(n,k) to be similar in modulo a shift in their indices. The first entries of the matrix b(n,k) are given by and ; where
Table 3. The first entries of the matrix b(n, k).
Table 4. The first entries of the matrix b(n,k).
We now record the main properties of the above matrix.
PROPOSITION 3
The coefficients b(n,k) have the following structure
| 1. | b(n,k)=0 if 0≤n≤4k+2. | ||||
| 2. | b(4k+3,k)=k!. | ||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
The proof is similar to the previous one and therefore is omitted. From the boundary conditions follows
and the recurrence relation reduces to
Observe that b(n,k) and c(n-1,k) depend on the same combination of the qk for example
3. Properties of c(n, k) and b(n, k)
We now show that qm appears linearly in the coefficients c(4k+5+m,k) and b(4k+7+m,k).
PROPOSITION 4
For , we have
(13)
where
(14)
and
and
are nonlinear functions of
.
Proof
To prove formula (3.1), we have to use induction on both indices m and k. First, for and from Proposition 1 we have c(4k+6,k)=-(k+1)!q0, which agrees with (3.1) for all k≥0.
Now for k = 0, we have to show that it is true for all m≥0. Now, since we have
The second term on the right hand side is a nonlinear sum of
To continue, we need to recall that
and the following assumption:
has the structure in (3.1) for all m≥0. and 0≤l≤k-1.
We need to show that (3.1) holds for
By the previous assumption, the second term on the right-hand side can be written as
Also, use from Proposition 1
and c(4k+2,k)=k!, to obtain
Adding the first and the second terms, we get
where the last two terms are only the nonlinear terms and thus are included in
The proof of the second identity is similar, and therefore omitted.▪
We now estimate the coefficients a(m,k) and d(m,k).
PROPOSITION 5
The coefficients a(m,k) and d(m,k) are bounded by
Proof
Denote the following sum of binomials by
From (3.2), we have
Using the classical identity
and the fact that
and
, we deduce that
and
Practical bounds can be derived from the binomial coefficients
For a fixed m, all entries of the form c(4k+m, k) have the same structure for the same m.
PROPOSITION 6
For k ≥ 0, we have
(15)
where the sequence
depends on m only.
Proof
To prove this proposition, we again use induction on m and k. It has been shown in Proposition 1 that
So, (3.3) is certainly true for m=0,1,… ,9 and all k≥0. We have to show that (3.3) also holds for c(m,k) where it has been assumed that it holds for
| 1. |
| ||||
| 2. | | ||||
The initial coefficient is given by
and by (2) it can be written as
Using the recursion formula, c(4k+m,k) is given by
The second term satisfies (3.3) by assumption (2) i.e.
The first term is a combination of , and by assumption (1), should contain the same elements appearing in
since all
contain the same strings of qk as the first one in c(l,0). Therefore c(m,0) and c(4k+m,k) contain the same strings of qk
which prove this proposition. Observe that we have used the recursion (2.9), which is valid for both sequences c(n,k) and b(n,k). Thus, a similar structure follows for the b(n,k)
In order to prove convergence of the iterates, we need estimates of the coefficients c(4k+m,k).
PROPOSITION 7
Assume that , then we have for all m≥6, k≥0,
(16)
Proof
We first prove (3.4) for c(n,k). We already know from Proposition 2, that
and so (3.4) is true for the first m. Now suppose that (3.4) is true for
| 1. |
| ||||
| 2. | | ||||
From the relation
and assumptions (i) and (ii), we deduce that
A simple estimate of the binomial coefficients
yields
since
The proof for the upper bound of b(n,k) is similar, and therefore omitted.▪
4. The truncation error
We now need to prove an estimate on the decay of the Taylor coefficients, as done in Citation3. From the expression
where
represents the weighted sum of the kth row of the matrix c(n,k). Recall that the solution y(b,λ) is entire of order 1/4 in λ and of type b; in other words we have
and this property can also be translated in terms of the coefficients Citation1, p. 131], by
or,
(17)
Observe that multiplying by λ5 would not change the type or order, and so,
which leads to
(18)
In the inverse problem, we shall be given the value of the Taylor coefficients
and since we shall use only the first four coefficients, we would like to estimate the convergence rate of remainder which we denote by
i.e.
(19)
Thus, using
After taking limits ( as
and using (4.2), it follows that the following limit exists, say L
PROPOSITION 8
Assume that then
as
.
It is precisely the above proposition that allows us to prove convergence of the method.
5. Discriminants
The coefficients c(n,k) and b(n,k) in the expansion of the solution and
of the boundary value problem (2.1) are used to compute the spectra for a given choice of the constants h and k. Since the solution is a combination
, we have
where Ui are the boundary conditions at x = b as defined in (1.1)
The above system has a nontrivial solution if
which reduces to (omit λ)
Thus, the discriminant Δh,k, can be written in terms of
where
Knowing h, k, and Δi is enough to define Δh,k and so the spectrum of (1.1). Recall that the zeroes of Δh,k form the spectra and can easily be computed when the expressions for
and
are available. The four spectra can be obtained by choosing four different values of h and k, for example
Therefore, if we are given four different functions i=1,…,4 i.e. four spectra while
(20)
we can then recover each of the building blocks Δi.
Use the fact that
to obtain
from which follows
(21)
6. The inverse problem
Assume that we are given four spectra which represent the zeroes of the entire functions
=1,…,4 where the choice of hi, ki satisfies the condition (5.1). Then we can recover each of the functions Δj, for j=1,…,4 as the solutions of the algebraic system
Observe that since each factor, or
making up the discriminants Δj is an entire function of λ, of order
and of finite type. This implies that Δj is also entire of order
and so in its Hadamard representation theorem, the polynomial g can only be of degree 0, i.e.
is a constant. Thus we deduce
Thus without loss of generality we can assume that we are given the functions Δj, instead of the spectra σj or the discriminants which can be expressed as
By identifying the coefficients like from (5.2) we deduce that for k≥0
(22)
The issue now is to recover the coefficients c(n,k) and then qk from the above infinite nonlinear system. Here we opt for a sequential algorithm and recover only a finite number, say the first 4m coefficients of q(x). According to Proposition 4, the last coefficients in the above system that would include all are
and
. Thus we need to use only the coefficients c(n,k) for n≤ 4m+5 and b(r,k) for r≤4m+6
The remaining coefficients that are to be moved to the right-hand side, are given by
Since we are dealing with analytic functions, is the tail of the series and so for i=1,2,3,4 and for each fixed k, we have
This means that for large m, is negligible, and an approximation is obtained by solving the following reduced system where
The above nonlinear system consists of 4m equations with 4m unknowns, which we shall decompose into m 4× 4 linear systems as follows: First extract the terms containing the first four highest indices for qi by setting r = 0 and choose the lowest i. Observe that b(3,0)=1
where Ri(m,k) contains lower-order terms. Observe that the b(n,k) involved in the above matrix reduces to constants and so are replaced by their values and contain no qk. After simplifying, we obtain
(23)
where we use Proposition 4 to extract the linear terms from each c(n,k),
where
contains nonlinear combination of the remaining coefficient
, which will be part of the right-hand side of the new system. Thus, system (6.2) can be written as a 4× 4 linear system
(24)
where the A(m) is a matrix given by column vectors extracted from (6.2)
(25)
The determinant of the matrix A(m) is explicitly given by
(26)
where
and
It is easy to check that
and so it follows that
exists for large m if
It is readily seen that Cramer's rule is applicable, as long as the polynomial for m∈N. Using Descartes' rule of signs Num(m,b) has no positive zeros if
which we shall assume to be true in all that follows.
We now outline the algorithm to solve the inverse problem. Assume we want to compute 4m Taylor coefficients,
First, we compute by setting k=m-1, in (6.2) and so we need only
, and δm-1 to get Fi(m,m-1). Recall that the system is upper triangular and these entries are located in the lower-right corner which is easily solved. Next, we use the newly obtained
to update
and then solve for
and so on. In the mth step, we recover the last four coefficients
The above recovered 4m coefficients are used to construct an approximation of q(x), which we denote by
(27)
and denote by
(28)
the exact function. We have the following theorem for the first coefficients
which are needed for the second step.
THEOREM 1
Suppose that the coefficients , and
are given, and
If
then we can recover
, which approximates
and
Proof
Recall that solutions are the solutions of the full system
(29)
while qk are the solutions of the truncated system (6.3).
Since the inverse A-1(m) exists, it follows that
(30)
We need to show that the first iterates converges to the exact solution if m→∞, i.e.
which would then force the second iterates to converge. To this end, set k=m-1 which implies that
, and so (6.9) becomes
(31)
since
for j=1,…,4. Using Cramer's rule,
is computed explicitly. Although A-1(m) exists, it may become unbounded as m gets larger. Fortunately, by using computer algebra system, A-1(m) can be computed explicitly since A(m) is known explicitly and is only 4× 4. Observe that
, which appear in (6.10) are a finite combinations of
defined in (4.3), and by tracking the different powers of m, this leads to the following estimate of the solution of (6.10)
On the other hand, from Proposition 5, we have
which yields for large m the following lower bound
and thus,
(32)
Use Proposition 8, which says that
to deduce that
Thus we have proved that 0 as
Use again the same argument to obtain the convergence of the other of first four coefficients
, and
as
Now, if we assume that
(33)
then the convergence for the next four terms
follows from (6.9), as it is easily seen that the right-hand side depends on the convergence of the previous terms.
From assumption (6.12) and since Fi are polynomials, it follows that for m large enough
is small, which in turn should give an approximation in the next iteration. Thus we can recover the coefficients by groups of four at a time
7. Examples
We now describe the computational algorithm. In all the examples in this section, we shall take the interval [0,1] and therefore b=1. We shall compute the polynomial QN(x) whose degree is N − 1, and this requires systems which are preloaded, since the coefficients c(n,k) are known. From the spectra, we compute symbolically the discriminants Δj. To this end, since q is analytic, we use the command [dsolve type power series type or powsolve in Maple], which quickly returns the solutions ϕ(b,λ), ψ(b,λ), and their derivatives. Then we can form the polynomial Δj and the command [Taylorcoef] gives the sequence of Taylor coefficients
γk, and δk. At the start the command [Order] is a function of N, and controls the degree of the polynomials used in the algorithm.
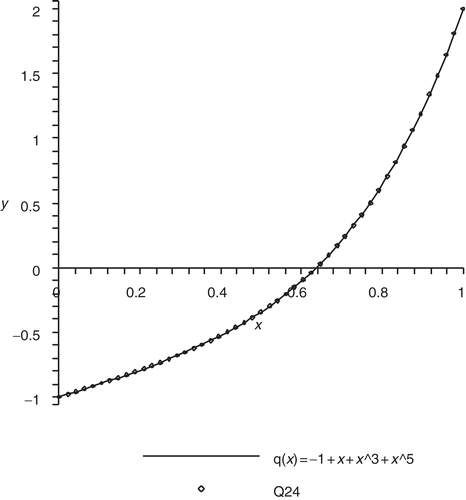
Example 1
Here we recover
from four sets of data
that correspond to the Taylor coefficients of the discriminants Δifor i=1,…,4. We shall recover
which is a polynomial of degree N − 1. The Taylor coefficients for Q12 are obtained by solving three 4× 4 systems sequentially. Observe that the coefficients get closer to the exact values as we increase N.
Table 5. Coefficients qk when N=12.
Table 6. Coefficients qk when N=20.
Table 7. Coefficients qk when N = 24.
The coefficientsq15=167090310.77825295621 seems to be large. However its contribution in q(x) is small because of the large denominator 15!
The error in the last two rows is compounded, due to the nature of the algorithm that uses the previously computed value to update the next system. Here we show how CAS uses rational numbers throughout to avoid any extra roundoff error
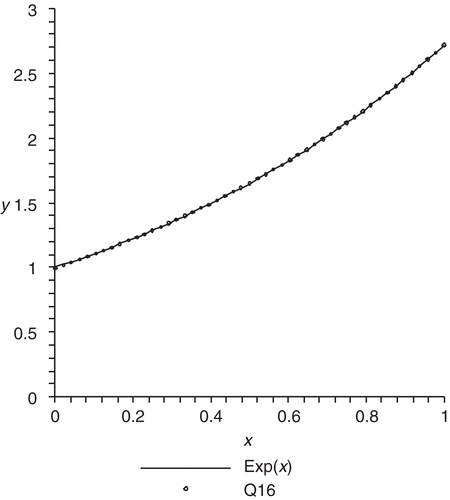
Example 2
Here we try to recover . This is an easy case to verify as
for all k≥0. We have obtained the following coefficients;
Table 8. Coefficients qk when N = 12.
Table 9. Coefficients qk when N = 16.
Table 10. Coefficients qkwhen N=24.
Table 11. Coefficients qk when N=12.
Table 12. Coefficients qk when N = 16.
Table 13. Coefficients qk when N = 24.
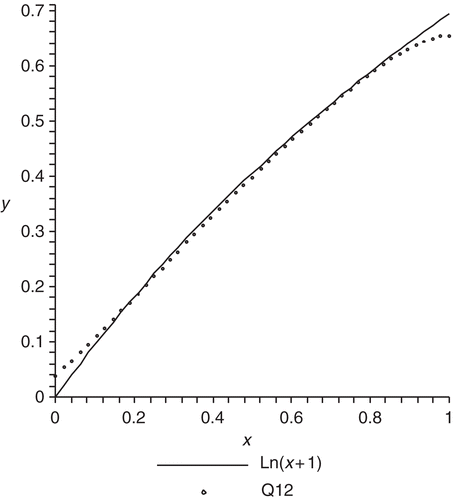
Example 3
Here we try to recover the nonanalytical potential, . Clearly, although the theorem is not applicable since q is not entire. Here, convergence is very slow.
This was made possible since the entries of the matrix A and A−1 were known explicitly in terms of rational numbers, see (6.4).
References
- Achieser, NI, 1992. Theory of Approximation. New York: Dover; 1992.
- Barcilon, V, 1976. Inverse problem for a vibrating beam, Journal of Applied Mathematics and Physics (ZAMP) 27 (1976), pp. 347–358.
- Boumenir, A, 1999. The recovery of analytic potentials, Inverse Problems 15 (6) (1999), pp. 1405–1423.
- Freiling, G, and Yurko, V, 2001. Inverse Sturm–Liouville Problems and their Applications. New York: Nova; 2001.
- Gladwell, G, 1986. The inverse problem for the Euler–Bernoulli beam, Proceedings of the Royal Society of London Series A 407 (1986), pp. 199–218.
- Hryniv, R, and Mykytyuk, YV, 2004. "Inverse spectral problems for Sturm–Liouville operators with singular potentials. II. Reconstruction by two spectra". In: Functional Analysis and its Applications, North-Holland Mathematical Studies. Vol. Vol. 197. Elsevier: Amsterdam; 2004. pp. 97–114.
- Levitan, BM, 1987. Inverse Sturm–Liouville Problems. Utrech: VNU Science; 1987.
- McLaughlin, JR, 1986. Analytical methods for recovering coefficients in differential equations from spectral data, SIAM Review 28 (1986), pp. 53–72.
- McLaughlin, JR, 1976. An inverse eigenvalue problem of order four, SIAM Journal of Mathematical Analysis 7 (5) (1976), pp. 646–661.
- Rundell, W, and Sacks, P, 2004. Numerical technique for the inverse resonance problem, Journal of Computational and Applied Mathematics 170 (2004), pp. 337–347.
- Sakhnovich, L, 2001. Half-inverse problems on the finite interval, Inverse Problems 17 (3) (2001), pp. 527–532.
- Yurko, VA, 2000. Inverse Spectral Problems for Differential Operators and their Applications. Amsterdam: Gordon and Breach; 2000.