Potential energy function from second virial data using sensitivity analysis

Abstract

Retrieving the potential energy function from second virial data, and using the sensitivity analysis approach is discussed in this work. A potential energy function, with an initial average error of 92%, in temperature range of 100–500 K, with respect to a reference potential, was considered as an initial guess. Within the present framework it was possible to produce another potential with an average error of 0.7 and 2.7%, using two regularization methods. Analysis of the sensitivity matrix has shown to be an important step while inverting the data. This preliminary analysis provides important informations about the optimal temperature and coordinate range to be used in the inversion process.

Keywords:

• Second virial data
• Sensitivity analysis
• Inverse problem

1. Introduction

The mathematical formulation of a phenomena is generally expressed as K f =g, in which g represents an observable quantity, f characterizes the system and K is a nonlinear operator between these two quantities. Obtainment of g, from K and f, represents what is called a direct problem, whereas extraction of f, from K and g is the inverse problem 1. The retrieval of the potential energy function from experimental data, such as from scattering data, spectroscopy and thermodynamics, is particularly important in physical chemistry.

The above inverse problem is known as an ill-posed problem, defined such that one of the three conditions (a) existence; (b) uniqueness or (c) continuity is not satisfied 2. In general, none of the above three conditions are satisfied. The inherent experimental error, together with the approximate model used to describe the phenomena, that is, K(f) ≈ g characterizes the solution of the inverse problem to be an ill-posed problem. As consequence, the representation of K will be ill-conditioned or rank deficient, which makes traditional methods, such as the Gaussian elimination or the LU decomposition 3, inadequate to handle inverse problems. Instead, more appropriate methods, such as the Tikhonov regularization 1 or the singular value decomposition 3, has to be used to find an adequate solution 1.

The expansion in terms of density for the compressibilty factor gives the relation between potential energy function and second virial coefficient, indicating this to be a nonlinear ill-posed problem. Nevertheless, an equivalent linear problem can be estabilished at the expense of introducing a singularity into the problem. Consequently, the inverse problem has to be solved in two stages; one to the right and the other to the left of this singularity. Each of these two parts of the potential is obtained by using recurrent neural network 4,5, singular value decomposition and the Tikhonov regularization 6,7. The problem has also been solved in a nonlinear form using recurrent neural network 8 and on the class of convex–concave functions 9.

In the present work, a functional sensitivy analysis approach will be used to obtain the Ar–Ar potential energy function from second virial data. Although the original problem is also transformed in a linear one, no singularity is involved and the whole potential can be obtained in an iterative procedure. The sensitivity matrix, connecting potential energy with second virial coefficient, will be analysed with respect to the temperature and potential energy ranges. This will indicate which region of the potential would be adequate to be inverted in a set of experimental data.

2. The sensivity analysis approach

Sensitivity analysis approach will be applied to recover the potential energy function from second virial data using the equation of state in the form 10, (p/k_B T)=ρ +B(T)ρ², in which B(T) is the second virial coefficient 11 and the other quantities have their usual meaning. The relation between potential energy function, E_p(R) and the second virial coefficient is given by (1)

The above integral equation, in general terms is given by (2) in which x stands for the temperature and y for the coordinate. Discretization of (2(2) ), at x_j, gives approximately, , with f_i=f(y_i) and g_j=g(x_j. A change in g, with a correspondent change in f, can be written as (3)

Using with , (4)

The effect of change in g_j which affects the solutions f_i can be measured by the quantity J_ijΔ R_i, thereafter denoted by S_ij. In an integral form, equation (4(4) ) is equivalent to, (5)

or, in matrix notation, (6)

This equation can be used in the following manner:

1.	An initial guess, f0, is given for the unknown.
2.	The approximately experimental value, g0, is computed.
3.	The quantity δ g is calculated as the difference between the experimental data and g0.
4.	A correction to the initial guess can be evaluated as δ f = f S-1 δ g from which a new value for f is obtained.

Equation (5(5) ) is general and can be applied to any nonlinear problem with a due interpretation of the quantities. For the present problem f will be the potential energy function, E_p, and g, the second virial data, B

The original nonlinear problem is, therefore, transformed into a Fredholm integral equation of first order, which will be solved by the singular value decomposition method 3, with two filters factors. The sensitivity matrix is transformed into S= UΣ V^T in which U∈ ℜ^{m\times m} and V}∈ ℜ^{n\times n} are orthogonal matrices, whereas Σ∈ℜ^{m\times n} is a diagonal matrix. The columns of U and V will be represented, respectively, by u_ie v_i, and σ_i the diagonal elements of Σ. A general solution of (6(6) ) can be written as, (7)

with λ a regularization parameter and π_i,λ a filter factor, depending on the singular values and on the regularization parameter. Two special cases are possible for (7(7) ), corresponding to two different choices of the filter factor: (a) a filter factor equal to unity before a certain value, k, and zero after this value; and (b) a smooth filter which takes into account all singular values in decreasing order of importance, , a procedure equivalent to the Tikhonov regularization 1.

3. Results and discussion

Important information on the inversion to be carried out can be obtained by analysing some aspects of S(R,T), although it is more appropriate to use, instead, the matrix, S'=(/ dln (δ B))d ln (δ E__p). Analysis of the S' matrix will be easier, since it has information on relative values, rather than on absolute values, as in the S matrix.

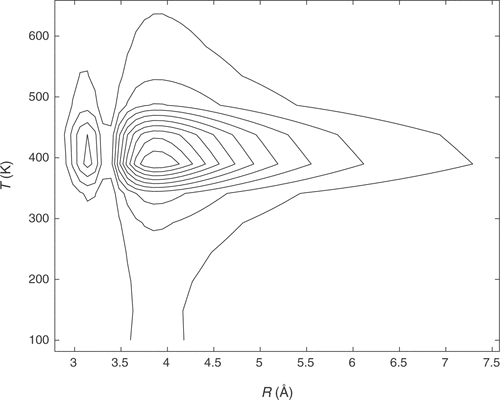
Level curves of the sensitivity matrix S' are presented in figure 1. In the region in which the sensitivity matrix assumes larger values it will be more stable to obtain the inverted potential. The opposite is also true. If S' reaches small values, E_p(R) will be more difficult to be obtain. The appropriate region for the inversion procedure is, therefore, promptly obtained from figure 1.

Figure 1. Level curves for the sensitivity matrix.

Simulated data were obtained by carrying the integration of (1(1) ) in the coordinate range 1.5–40 Å and temperature between 100 and 1500 K, using recent potential energy for Ar–Ar system 12. These data give and error of 4% when compared with the experimental second virial data. However, when analysing the inverted potential, one must be guided by the sensitivity matrix. This analysis gives the optimal region for the coordinate from 3 to 6 Å.

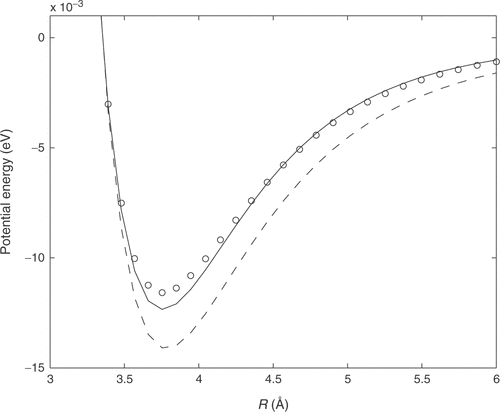
An initial guess for the potential energy function, which gives an error of 92% for the calculated second virial coefficient, was used to obtain a new potential from equation (7(7) ). In figure 2, the computed potential, using the truncated singular value decomposition, is compared against the initial guess and the potential from reference 12. The new potential gives an error of 0.7% for the calculated second virial coefficient, a value within the experimental error. In figure 3 the inverted potential was computed using the Tikhonov regularization, with 2.7% error in the computed B(T). The discrepancy principle 13 was used to calculate the optimal dimension of the subspaces and the optimal regularization parameter. The computed values are k = 7 and λ = 92.367 ųeV^-1, from which the potentials were calculated. Second virial coefficients from Aziz's potential 12, together with the values calculated from the inverted potentials are presented in figure 4.

Figure 2. Potential energy function from reference 12 (full lines) initial guess (dashed lines) and inverted potential energy function (o). Results are computed using the singular value decomposition.

Figure 3. Inverted potential using the Tikhonov regularization. Labels as in previous figure.

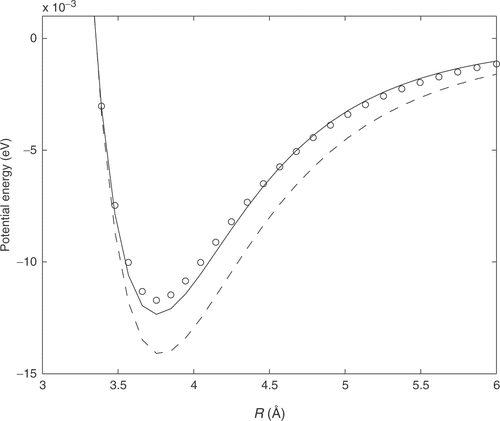
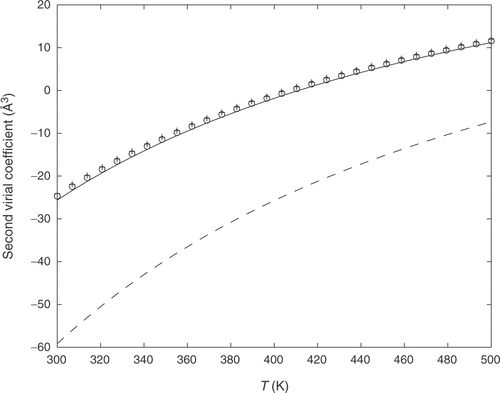
Figure 4. Computed second virial coefficient from reference potential 12 (full line), inverted SVD potential (o), inverted Tikhonov (+) and from the initial guess potential (dashed line).

Although both potential gives basically the same error for the second virial coefficient, their quality can be better appreciated by computing the error of these new potentials with respect to the potential of reference 12, taken as exact. In the region from 1.5 to 40 Å the relative error are of the order of 10³. This is not taken to imply the potentials are not of quality to describe the property being inverted. As inferred by the analysis of the sensitivity matrix the results have to be considered in the region where information can be obtained, that is, between 3 and 6 Å. In this region the potential from figures 2 and 3 gives, respectively, the errors 0.6 and 0.5%. The error in the initial guess, inside this region, is 27%, showing the improvement of the potentials.

4. Conclusion

The functional sensivity approach was used to recover potential energy function from simulated second virial coefficient. Unlike in the Keller and Zumino approach 7 the present functional linearization introduces no singularity in the new integral equation, providing a single procedure, as in the previous nonlinear approach 8, to recover the complete potential.

An optimal region, for the temperature and coordinate, can be inferred from the sensitivity matrix. In this case, the optimal coordinate range coincides with the one obtained previously for the same potential 8. Further insights on the inversion process can be obtained by using the singular value decompostion inversion. For large values of the basis set, and outside the optimal region, more oscillation occurs in the basis functions. It is clear, therefore, that the basis better represents the potential in the optimal region. Since the singular values decays to zero, the basis will be amplified outside the region.

The analysis on the singular value basis v_i reinforced by the previous analysis on the matrix S, indicates the region where inverted potential has to be considered. With an initial guess for the potential energy function, containing an average error of 92% for the second virial data, another potential was recovered, under the above analysis, with an average error of 0.7% for Tikhonov regularization and 2.7% for truncated singular value decomposition.

A general strategy to handle other nonlinear problems is also provided by the sensitivity approach. For example, the determination of the potential energy from scattering data can be tackled by the present approach. Even in situations where the kernel is unknown, the sensitivity matrix can be constructed by experimental or simulated data.

Acknowledgment

This work was supported by Counselho Nacional de Desenvolimento Cientifico e Tecnológico (CNPq).