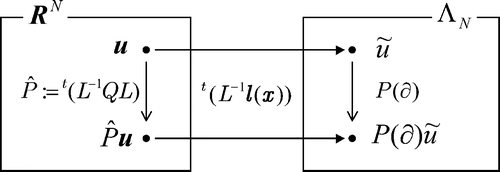Abstract
Inverse heat conduction problem consists of finding an initial temperature distribution from the knowledge of a distribution of the temperature at the present time. Here, we assume that the associated boundary conditions are known. The heat conduction problem backward in time is a typical example of ill-posed problems in the sense that the solution exists only for regular functions of some kind describing the present temperature distribution and also the solution is unstable for the present temperature distribution function. Conventional numerical methods often suffer from instability of the problem itself when high accuracy is intended in the approximation. Our aim is to create a meshless method which is applicable to the ill-posed inverse heat conduction problem. We construct a high order finite difference method in which quadrature points do not need to have a lattice structure. In order to develop our new method we show a tool in using exponential functions in Taylor's expansion. From numerical experiments we confirmed that our method is effective for solving two-dimensional inverse heat conduction problem numerically subject to mixed boundary conditions.
Nomenclature
| D | = | domain in R2 |
| L, Q | = | matrices on RN |
| lj, l(x) | = | vectors of RN |
| m | = | dimension |
| N | = | total number of quadrature points |
| N | = | the set of natural numbers |
| n(x) | = | outward unit normal on ∂Ω |
| P(ξ) | = | polynomial in ξ |
| P(∂) | = | differential operator |
| = | Neumann data | |
| R | = | the set of real numbers |
| u | = | solution of the problem |
| u | = | vector of approximate solution |
| uF | = | final data |
| = | Dirichlet data | |
| w(x) | = | vector of weights |
| x, ξ | = | points in Rm |
| x(j) | = | the jth quadrature point |
| Z+ | = | the set of non-negative integers |
| α | = | multi-index |
| = | a part of ∂Ω | |
| Δ | = | Laplacian |
| Δ x1 | = | lattice width in x1 direction |
| Ω | = | domain in Rm |
| ∂ | = | gradient operator |
| ∂Ω | = | boundary of Ω |
1. Introduction
We take a bounded domain D in R2 and a space–time domain Ω =D× (0, T) in R3 for a final time T > 0, where D represents a heat conductor. A point in the space–time domain Ω is written by for the sake of conciseness. We write Γd=ΓB∪ ΓF by using two surfaces ΓB=∂ D× [0, T] and ΓF=D×{T} of the boundary ∂Ω. The boundary ΓB moreover consists of surfaces ΓB1⊂ΓB and Γ B2=Γ B∖ Γ B1. Then for given Dirichlet data
, Neumann data
and final data uF: Γ F→ R, we consider a problem to look for a function u(x) that satisfies
(1)
(2)
and
(3)
Here, the symbol Δ denotes the Laplacian
. An outward unit normal of the boundary ∂D at x is denoted by
. We say that the problem in (1–3) is a two-dimensional backward heat conduction problem under the mixed boundary conditions (2).
The backward heat conduction problem is ill-posed in the sense that the solution does not always exist for any final data uF. It is known for one-dimensional backward heat conduction equation in Citation1 for 0<x<1, t≤T with
that the final data u(x, T) is required to belong to the function space
for the existence of the solution u(x, t).
The backward heat conduction problem is also ill-posed in the sense that the solution is unstable for given final data uF Citation2. As a matter of fact we illustrate instability of the problem: let the domain D be (−π , π )× (−π , π ). We set Γ B1=Γ B and Γ B2=φ. We prescribe the final data , x∈Γ F and the boundary data
, x∈ Γ B for an l∈N. Then the exact solution of the heat equation (1) is given by
. We choose the two L2 norms
for functions u: Ω → R and v: ΓF→ R, respectively, where
. The solution can be estimated as follows.
(4)
Since for any C > 0 we can choose l∈N such that
, the inequality
holds for any C > 0. This means that the solution does not depend on the final data continuously in the L2-sense. Therefore, the solution of the backward heat conduction problem is unstable for the final data.
In order to solve the backward heat conduction problem numerically, we consider an application of conventional finite difference schemes. For any time step size Δ x3>0 in the time range [0, T] and for any lattice widths Δ x1>0 and Δ x2>0 in each direction of x1 and x2 in D, we know by the von Neumann condition Citation3 that the following finite difference scheme, explicit backwards, approximating the equation (1) is unstable.
(5)
We note that the following scheme, implicit backwards, is also unstable.
(6)
We state a motivation for our research. There are a number of researches which challenge to analyze ill-posed problems numerically. For example, techniques are described in Citation4,Citation5 for making both the discretization error and rounding error arbitrarily small by using the spectral collocation method and an arbitrary precision arithmetic, respectively. The backward heat conduction problem is solved very precisely under no observation errors by their techniques. However in the spectral collocation method, the Chebyshev–Gauss–Lobatto points Citation6 are employed as quadrature points for the inversion. Therefore it is difficult to apply the techniques to the problem on a domain with curved boundaries. As an applicable method for engineering problems, we propose a more flexible high order finite difference scheme instead which allows quadrature points at arbitrary locations.
2. Notation
We introduce a set and let
, where Z denotes the set of all integers. Then an element
is called a multi-index. A symbol 0 denotes (0, 0,… , 0). For the multi-index
, a few operations and relations are defined in the following: A length of α is defined by
. Let
be a vector in Rm. We distinguish the aforementioned length of a multi-index |·| from the length of the vector
. A power of x is defined by
. A factorial of α is defined by
. A differential symbol
is meant by
operated to sufficiently smooth functions. Setting
and
formally, we write
.
3. Finite difference approximation
In this section, we introduce a finite difference approximation to the derivatives. Let u be an analytic function defined on a convex bounded domain Ω ⊂Rm into R. Namely, the function u can be expanded into the Taylor series
(7)
in the sense of absolute and uniform convergence for any compact subset of Ω. We take a point
and N quadrature points
for j=1, 2,…, N randomly in Ω. For real constants aα for α in
, we set a differential operator P(∂) of order μ0 as
(8)
where aα=0 for |α |>μ0 with some μ0∈N. We consider approximating the value P(∂)u(x) at the point x by using a linear combination of values u(x(j)), j=1, 2,…, N. More specifically, by choosing weights
appropriately, we try to represent the value P(∂)u(x) as
(9)
where ϵ (x; P(∂)u) denotes a discretization error. We call the approximation (9) a high order finite difference approximation of P(∂) with respect to the quadrature points x(j) j=1, 2,…, N for larger N.
Concretely we can determine the weights wj(x), j=1, 2,… , N as follows. Substituting the operator (8) to the equality (9), we can see that the left hand side of the equality (9) becomes
(10)
From Taylor's expansion (7) the first term on the right hand side of the equality (9) becomes
(11)
From relations (10) and (11), the error in equation (9) can be written as
In the conventional finite difference approximation, weights wj(x), j=1, 2,…, N are given by a solution of the linear system
(12)
for the largest possible integer μ.
Here, we take the following trick in order to choose the weights: let ξ (i), i=1, 2,…, N be vectors in Rm such that for i≠j. Multiplied by
and summed up for all
, the equality (12) becomes
(13)
Generally, the equality
(14)
holds. By the equality (14) and a polynomial
, ξ ∈ Rm, the equality (13) is transformed into
, or equivalently
(15)
We set a column vector
for j=1, 2,…, N and construct a matrix
. Moreover we set a diagonal matrix
with Kronecker's symbol δij and two column vectors
and
. Then we can write the linear system (15) as
(16)
Therefore the weights wj(x), j=1, 2,…, N are given by
(17)
provided that L is invertible. By using a vector
the high order finite difference approximation (17) is thus represented by
(18)
4. Exponential interpolation
We characterize our high order finite difference approximation (9) by showing a relation between an exponential interpolation and the high order finite difference approximation.
Let a function be a linear combination of exponential functions and be equal to the function u at each quadrature point x(j) for j=1, 2,…, N. More specifically, there exist constants bi∈ R, i=1, 2,…, N such that
with a vector
. We call the function
an exponential interpolation in u at the point x(j), j=1, 2,…, N. Since
, the coefficients of the linear combination become
. Therefore the exponential interpolation
can be written by
(19)
Now we operate P(∂) on both sides of the formula (19). From the equality
, we obtain
(20)
Furthermore, from an equality
, the equation (20) becomes
We see from this expression and (19) that the matrix
is a counterpart to the differential operator P(∂) through the exponential interpolation. In , we illustrate the equivalence of the matrix
and the differential operator P(∂) inside the space
.
Figure 1. Equivalence of and P(∂).
Here, we illustrate an approximation of a derivative numerically by using the exponential interpolation. From the equality (20), the high order finite difference approximation (18) is represented by
(21)
When the dimension m = 2, we randomly locate quadrature points
, j=1, 2,…, N and set
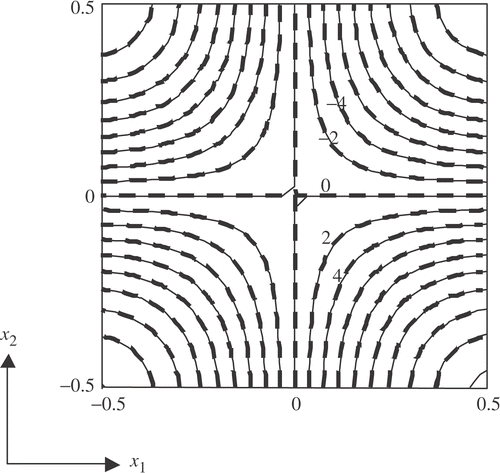
, i=1, 2,…, N. We take a function
and a differential operator
the Laplacian. In the approximation
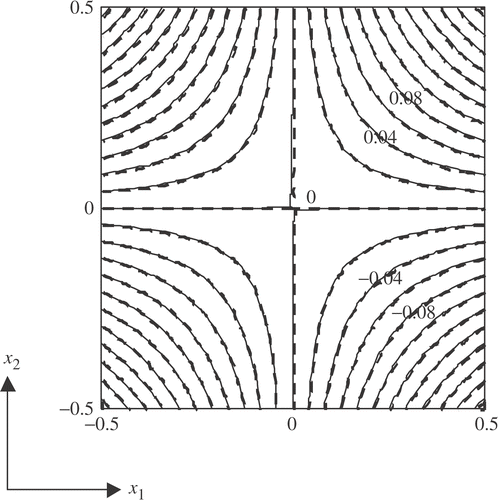
for N = 100 and the derivative
are presented by their contour lines. We see that the approximation agrees well with the true derivative. In fact, the maximum error
is 7.0× 10−2. From this numerical example we can expect that the error in the derivative is small in the high order finite difference approximation.
Figure 2. (—) and
(- - -).
5. High order finite difference method
We use the finite difference approximation (9) in our method to solve backward heat conduction problems (1–3) numerically.
Let quadrature points belong to the closure
of the domain Ω. We set differential operators
and data
for k=1, 2,…, N, where I denotes the identity operator. We restrict the domain Ω considered in the problems (1–3) onto the set of quadrature points x(k), k=1, 2,…, N to obtain
(22)
Let uj be an approximate value of the true u(x(j)) for j=1, 2,…, N. We set vectors
, i=1, 2,…, N for a parameter ρ > 0. Then we consider finding the approximate values uj, j=1, 2,…, N from the given data fk, k=1, 2,…, N based on the equalities (22).
Let k∈{1, 2,…, N} be fixed arbitrarily. From the high order finite difference approximation
(23)
we can calculate weights wkj, j=1, 2,…, N as follows. Since weights in the approximation (9) are determined as a solution of the equation (15), we set weights wkj, j=1, 2,…, N as a solution of the linear system
(24)
From the equations (22) and the approximation (23) it is suitable to find approximate values uj, j=1, 2,…, N as the solution of the linear system
(25)
Setting a matrix
and two column vectors
,
, the linear system (25) is represented by
. Therefore, approximate values uj,j=1, 2,…, N are given by
(26)
We call the above method a high order finite difference method.
6. Numerical results
We apply the high order finite difference method to the backward heat conduction problems (1–3).
6.1. Heat conduction with a Fin
Let the domain D be and the final time be T = 1. We set
and
. The outward unit normal n(x) of ΓB2 is represented by
. For a parameter
the function
with respect to x satisfies the heat conduction equation (1). For
we give the boundary data and the final data exactly as
at x∈ΓB1,
at x∈ ΓB2, and
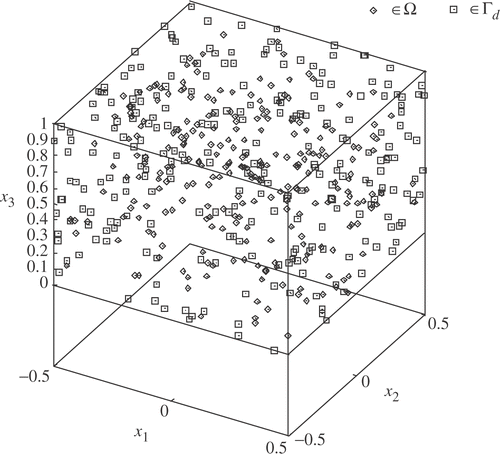
at x∈Γ F. Then we calculate numerical solutions of the problems (1–3) by using the high order finite difference method for N = 500 and ρ = 3.
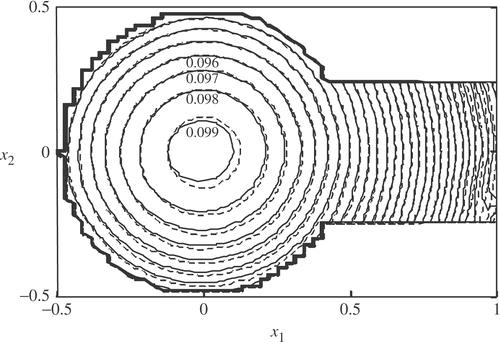
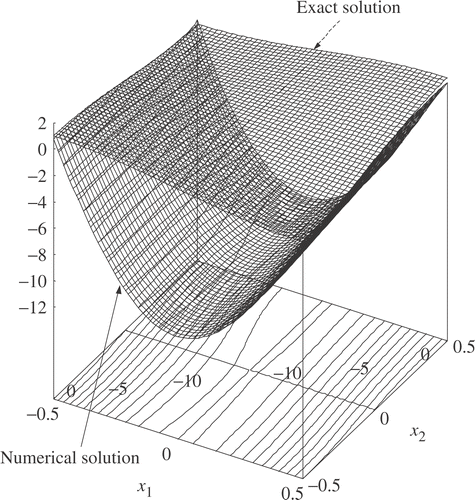
We show the numerical solution and the exact solution in at x3=0.5 and in at x3 = 0. At x3 = 0 the error of the numerical solution is . Accordingly, for the problem in which the domain is not rectangle, we can obtain the accurate numerical solution.
Figure 3. Numerical (—) and exact (- - -) solutions (x3=0.5).
Figure 4. Numerical (—) and exact (- - -) solutions (x3 = 0).
6.2. Heat Conduction in a Square
Let the domain D be (−0.5, 0.5)× (−0.5, 0.5) and let the final time be T = 1. We set boundaries and
x2=−0.5, 0.5}. For a parameter l∈N the function
satisfies the heat conduction equation (1). We prescribe the boundary data and the final data exactly as
at x∈ΓB1,
at x∈ ΓB2, and
at x∈Γ F. Then we calculate numerical solutions of the problems (1–3) by using the high order finite difference method for the number N = 500 of quadrature points.
In , the distribution of quadrature points is presented.
Figure 5. Quadrature points.
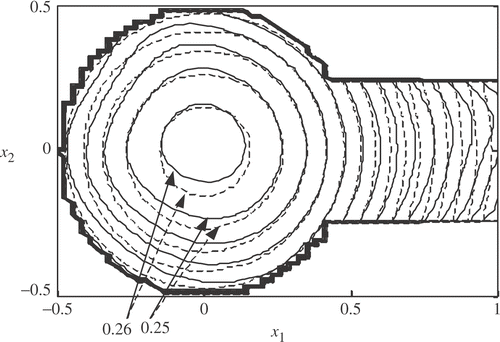
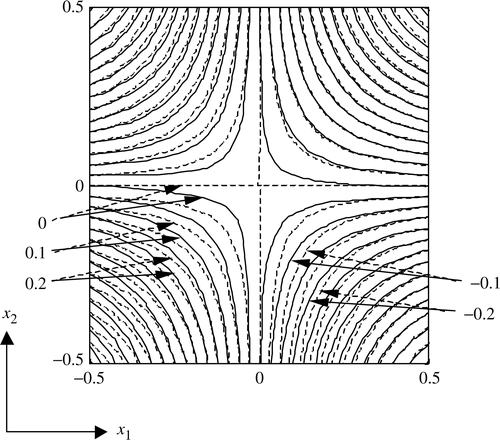
We show the exact solution and the numerical solution for ρ = 4 at x3 = 0 in figures for l=1, 2, 3, respectively. Each error in the numerical solutions is 1.6× 10−4, 2.4× 10−2, and 8.2 respectively for l=1, 2, 3, where error is defined by . We observe an increase in the error of the numerical solutions as the parameter l becomes large. In particular, the error on the boundary ΓB2 is larger than the error in the vicinity of the boundary ΓB1.
Figure 6. Numerical (—) and exact (- - -) solutions (l = 1, x3 = 0).
Figure 7. Numerical (—) and exact (- - -) solutions (l = 2, x3 = 0).
Figure 8. Numerical and exact solutions (l = 3, x3 = 0).
In , the difference between the numerical solution and the exact solution is considerably large. From the estimation (4) the ratio between the solution u(l) and the final data is
with respect to L2 norm. For l=2, 3, the ratios are estimated as C2≈700 and C3≈107, respectively. As a source of the large error in the numerical solution for l = 3 we guess an accumulation of round-off errors in the computational arithmetic.
7. Conclusions
We considered a high order finite difference method in order to solve the backward heat conduction problem. The high order finite difference approximation is based on the idea that the derivative of an unknown regular function can be approximated with high accuracy by a linear combination of values of the function at quadrature points. Since we use the quadrature points which can be chosen at arbitrary locations, the method gains a meshless property. It is shown that the approximation coincides with the derivative of the exponential interpolation. In numerical experiments, the two-dimensional backward heat conduction problem was solved as a three-dimensional problem in the space–time domain. When magnification of the solution to the final data is very large, we guess that the numerical solution can conceivably be influenced by round-off errors. We confirmed that our method is applicable to the problem in the domain with curved boundary under the mixed boundary conditions.
References
- Yamamoto, M, 2002. Introduction to Inverse Problems. Tokyo: Iwanami-Shoten; 2002. p. 77, (in Japanese).
- Kress, R, 1989. "Linear Integral Equations". In: Applied Mathematical Sciences. Vol. 82. New York: Springer-Verlag; 1989.
- Richtmyer, RD, and Morton, KW, 1967. "Difference Methods for Initial-value Problems". In: Interscience Tracts in Pure and Applied Mathematics. Vol. 4. New York, London, Sydney: Interscience Publishers; 1967.
- Imai, H, Takeuchi, T, and Kushida, M, 1999. On numerical simulation of partial differential equations in infinite precision, Advances in Mathematical Sciences and Applications , Gakkõtosho 9 (2) (1999), pp. 1007–1016.
- Fujiwara, H, and Iso, Y, 2001. Numerical challenge to ill-posed problems by fast multiple-precision system, Theoretical and Applied Mechanics Japan 50 (2001), p. 419.
- Canuto, C, Hussaini, MY, Quarteroni, A, and Zang, TA, 1988. Spectral Methods in Fluid Dynamics. New York: Springer-Verlag; 1988.