Optimal actuator placement for controlling concentration profiles via process tomography

Abstract

In this article, the optimal control of a chemical plant driven by an inverse problem is considered. More specifically, the problem of optimal actuator placement when controlling the concentration of a target substance in rapidly moving fluid is investigated. In this example, the actuators are injectors through which strong concentrate is injected into the fluid in order to obtain a desired concentration profile. The target substance is assumed to obey the stochastic convection-diffusion model and the process is monitored with electrical impedance tomography, the inverse problem of which is notoriously ill-posed even under stationary conditions. The associated reconstruction problem is formulated as a state estimation problem and is intertwined with the determination of the optimal time-varying controls. The model-based linear quadratic Gaussian control strategy is used in the determination of the control inputs. The controller settings affect both the overall controller capabilities per se and the performance of the controller via the embedded state estimation procedure. Although it is obvious that proper actuator setting can have a major impact on the control performance of the system, the optimisation has seldom been carried out over the entire controller chain which includes also the state estimation procedure. When the observation modality exhibits ill-posed characteristics, the state estimates may be rendered useless and the controls far from optimal. The studied case shows that the actuator setting affects the state estimation accuracy and the controller quality significantly.

Keywords:

• Process control
• Electrical impedance tomography
• Optimal actuator setting

1. Introduction

Nowadays, industrial processes must meet product quality requirements as well as demands on energy efficiency, reduction of environmental pressure and production expenses. These demands can be fulfilled with proper process design, efficient real-time monitoring systems and optimal control methods. Often adequate control performance relies strongly on accurate process monitoring. Process tomography is a non-invasive technique for monitoring the process progress. It provides quantitative information about the physical properties of the process based on indirect boundary measurements. This information can in turn be utilised in process control to determine the changes required in order to achieve the desired outcome.

The industrial applications that benefit substantially from using process tomography as a sensor in a control system include processes in which the monitoring of fast-moving fluids in pipelines is needed. Such applications are, for example, different kinds of liquid/liquid mixing 1,2 and solid/liquid mixing processes 35. The most common tomographic techniques in the field of industrial applications are electric methods. In this article, the imaging modality is electrical impedance tomography (EIT) 6.

Although control is usually stated as one of the main aims of process tomography 4,710, there have been only a few automatic model-based control applications employing process tomography as an observation modality. Also, the computational models used to obtain the tomographic reconstructions in process applications have traditionally been more qualitative than quantitative in nature. For example, in 11 a proportional-integral (PI) controller is utilised in controlling a pneumatic conveying system using tomographic imaging. In 12, a proportional-integral-derivative (PID) controller is applied to bubble column reactor. In these articles, the control is based on a sequence of stationary images assuming that the target does not change during the measurements.

When considering the problem of monitoring and controlling fast-moving fluids, the target changes very rapidly during data acquisition. In such a case traditional stationary reconstruction methods yield reconstructions that are useless. Inevitably, poor process monitoring leads to poor control performance. Therefore, in this article, the ill-posed inverse problem of EIT is formulated as a state estimation problem in which the EIT measurements are described in terms of the observation equation. In 1315, the state estimation approach is shown to yield superior reconstructions in comparison to traditional reconstruction methods when non-stationary targets are considered. For the state estimation approach, temporal prior information of the target is required. As the target has both spatial and temporal variations, the state evolution model is best described by a distributed parameter system (DPS) 16. In the case of rapidly moving fluids, fluid dynamical models can be utilised as an evolution model. In this article, the state is governed by a stochastic partial differential convection–diffusion (CD) model.

Since spatial discretisation is required to approximate the exact solution of the partial differential equation (PDE), and state reduction may lead to intolerable approximation errors, the state dimension of the problem is invariably very large. However, as the controller is implemented in real time, the computational complexity of the system has to be minimised. Thus, it is crucial to choose an appropriate and accurate approximation technique for the spatial discretisation. The key issue is to model the errors and uncertainties of the underlying state evolution model with adequate accuracy so that approximation and unavoidable modelling errors do not destroy the estimates. With modelling errors one refers to practical settings in which boundary data or parameters are not (exactly) known. For these quantities, feasible stochastic models have to be constructed and linked to the state evolution and observation equations. The associated state estimation problem can be solved with the Kalman filter or with its modification and extensions.

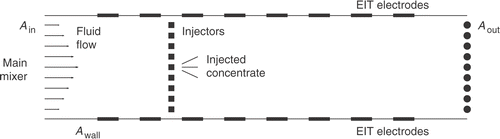
The objective of the proposed model-based control system illustrated in figure 1 is to regulate the concentration distribution of a substance in a fluid moving along a pipeline. The controller is designed to compensate for any possible low concentration inclusions in the fluid after a main mixer so that the concentration distribution over the output boundary A_out matches a desired uniform distribution as well as possible. A number of injectors are placed in the pipe as actuators and through these injectors strong concentrate is injected into the flow. The flow rates of injectors are considered as control variables, and they are determined based on the estimated concentration distribution that is obtained with the Kalman filter. The linear quadratic Gaussian (LQG) controller is utilised. In 17,18 the control system is described in detail. In these articles, numerical simulations showed that it is possible to base an automatic model-based control system on tomographic measurements. Also, controlling the concentration in fluid flow when using process tomography as a sensor is presented in 19. However, in these articles, attention is not paid on actuator setting even though control performance can be improved by locating the actuators in some sense optimal or at least near optimal locations.

Figure 1. Illustration of the measurement set-up.

In this article, an optimal actuator placement problem with a model-based LQG control strategy is considered. Inspecting the actuator setting is important since in some process control applications the limitation of efficient performance is due to poor selection and layout of actuators and/or measurement sensors. To some extent, the possible locations of actuators are defined by the physical characteristics of the process. For simple systems, the designer can choose the actuator locations based on physical intuition and experience. However, as the system becomes more complex geometrically or structurally, methods for optimising the actuator placement are required. In practice, simply trying out possible locations is too expensive and time-consuming. In this article, the optimal locations are, therefore, determined by inspecting appropriate performance criteria. Furthermore, not only the location but also the optimal number of actuators that provide the best or at least adequate performance has to be determined. The adequate control performance is of course dependent on the system and the control objective. It is obvious that as the number of actuators increases the control performance improves. However, in practical implementations, the maximum number of actuators is limited. One can consider, for example, the TrumpJet® injection system for mixing papermaking chemicals into the main process stream 20. The system is designed to operate with only a few injection points located at the pipe boundary. It is worth noticing, however, that this article focuses on the theoretical inspection of the optimal actuator problem and not on any specific application.

This article is organised as follows. In section 2, the observation model for the EIT measurements is reviewed. In section 3, the evolution model for the concentration in the case of CD processes is described. Using the evolution and observation models, the state space representation is constituted. The solution to the state estimation problem and the LQG controller is introduced in section 4. Also, in section 4 the performance criteria for optimal actuator placement are presented. The numerical simulations described in section 5 illustrate the benefit of the optimal actuator setting to the control performance.

2. Observation model

Electrical impedance tomography is a suitable modality for imaging targets that possess spatial and/or temporal variations in conductivity. In EIT, electric currents are injected into the object with unknown electromagnetic properties through a set of contact electrodes attached to the object boundary. The resulting potential differences, or voltages, between chosen pairs of electrodes are measured. The objective is to estimate the electrical conductivity distribution inside the object based on the measured voltages. The computation of the electric potential and the voltages given the contact impedances, the injected currents and the conductivity distribution is the forward problem of EIT. The inverse problem of EIT is to reconstruct the conductivity distribution based on a set of voltage measurements.

Let , n = 2, 3 be a bounded domain with L contact electrodes attached to the boundary A_wall. The electrodes are denoted by boundary patches e_ℓ⊂A_wall, 1≤ℓ≤L. When , the electrodes are disjoint intervals of the boundary. At time t = t_k, electric currents I^(ℓ)=I^(ℓ)(t_k) are injected into the object using these electrodes, and the resulting potentials U^(ℓ)=U^(ℓ)(t_k) on the electrodes are measured. The most accurate known model for the forward problem of EIT is the complete electrode model 21 (1) (2) (3) (4) where φ =φ(x) is the electric potential in Ω, z_ℓ is the known contact impedance between the ℓ^th electrode and contact material, and n is the outward unit normal. In addition, to ensure the existence and uniqueness of the solution (charge conservation and potential reference), the conditions (5) (6) are required. The main difficulty in using diffuse tomography is the ill-posedness of the inverse problem and the associated instability of the (stationary) estimation scheme, even when the observations are noiseless. Therefore, it is crucial that the forward model is adequately accurate.

The boundary value problem (16) has a unique weak solution that is approximated with the finite element method (FEM) 21,22. Usually, the conductivity distribution is approximated by piecewise constant functions in the FEM solution. However, the piecewise linear approximation is used in this article as in 14. This choice is adopted since it allows for a straightforward mapping between the state evolution and observation models.

Assume that the model describing the dependence between conductivity and concentration is . Let denote a finite dimensional approximation of the concentration at time t. The resulting observation model corresponding to current pattern at time t is of the form (7) where contains the voltage observations at time t, N_U is the number of voltage measurements corresponding to one current injection, maps the conductivity to the observed voltages corresponding to the current pattern I_t, and is the composite mapping . The vector is the observation noise at time t with a known covariance matrix Γ_vt. The covariance matrix Γ_vt is determined by analysing the measurement system properties, and the computation of Γ_vt on the basis of the measurements is discussed in detail in 23.

Since the control system is situated after the main mixer of the process, the concentration fluctuates only slightly around a best homogeneous concentration estimate c₀. Therefore, it is adequate that the mapping is linearised at c₀ in order to reduce the computational load. The effect of linearising the EIT observation model on control performance is discussed in 24. If the fluctuations in the concentration were large and thus, the non-linear observation model was used, the state estimation problem could be solved with the extended Kalman filter. The linearised observation model is (8) where the Jacobian is obtained using the chain rule of differentiation, . Here J_Rt and J_σ denote the Jacobians of the functions R_t(σ) and σ(c), respectively. The computation of the Jacobian J_Rt is considered e.g., in 22. When c and σ are approximated in the same FE basis, the Jacobian is a diagonal matrix .

There are several approaches for solving the inverse problem of EIT. In stationary EIT, it is assumed that the concentration distribution does not change during a set of current injections. The stationary reconstruction problem of EIT is an ill-posed inverse problem and the solution requires spatial prior information about the target 25,26. In the case of process control, however, the target usually changes between consecutive current injections, and the state estimation approach is more suitable. In state estimation, temporal prior information is utilised in the reconstruction. In the case of moving fluids, the fluid dynamical model can be used. In this article, the CD equation is utilised as an evolution model and it is described in section 3.

3. Evolution model

In this section, the state evolution model for the concentration in the fluid is described. Let , n = 2, 3, be the domain corresponding to the object of interest, in this case a finite segment of a pipe. The concentration distribution is denoted by c=c(x,t), x∈Ω and t ≥ 0. A single-phase flow through a segment of the pipe is considered, and it is assumed that the concentration satisfies the CD equation (9) where is the velocity field and κ =κ(x) is the diffusion coefficient. In practical situations, the actual flow in the pipe is often turbulent and non-stationary. In this article, the true velocity field is approximated with the time-averaged velocity for turbulent flow and the effects of turbulent mixing are included in the diffusion coefficient κ 27. The reasoning behind the associated approach is that as long as the observations and the overall stochastic structure of the evolution model are adequately accurately modelled, the state estimation and control scheme are relatively tolerant to mis-specifications of such quantities as the velocity field 17,28,29. The additional source term q=q(x,t)=Λu(t) in (9) describes the injection of the component being controlled into the flow. Here are the flow rates of the injectors, K denotes the number of injectors, and Λ is a linear map that depends on the geometry of the injecting system. Simply, assuming that the output of the injector j is uniformly distributed in a small volume V_j⊂Ω, j=1…K, (10) where |V_j| denotes the size of the volume. The concentration differences can be considered as a result of imperfect mixing of a component into a volume. A more accurate model for the injectors would also take into account the change in the velocity field due to the injections. This, however, would necessitate real-time computation of the velocity fields that are too time-consuming for a real-time implementation with fast sampling. Furthermore, assuming that the concentration of the injected substance is very high, the flow rates of the injectors are low. Hence, the change in the velocity due to the injections is relatively small.

The cutting surface at the end of the computational domain over which the concentration profile is regulated is denoted by A_out. The concentration at the boundary A_out is defined as (11) The input boundary A_in refers to the cutting surface at the start of the computational domain, and A_wall denotes the pipe walls. To solve the CD equation, the following initial and boundary conditions are required: (12) (13) (14) where c_in(x,t) is the time-varying concentration on the input boundary A_in and n is the outward unit normal. As it is assumed that the process is dominated by the convection term, it is reasonable to postulate an approximate boundary condition for the output boundary (15) as described in 14.

Although the input concentration c(x,t) is written as a Dirichlet condition, it is actually the primary unknown of the overall system model. Thus, c_in(x,t) is considered as a stochastic function (16) where is the deterministic part of the input, usually the spatial/temporal average of c_in(x,t) or its estimate. Furthermore, in equation (16) η(x,t) is a stochastic process whose statistics should approximate the actual fluctuations of the input. The inclusion of the state noise that is due to this term is one of the key ingredients that makes the state estimation feasible.

The FEM is used to approximate the solution of the parabolic PDE (9) with the initial and boundary conditions (1216). The FEM scheme of the CD problem without the control term is described in detail in 29. In the FEM, the concentration is approximated with spatially piecewise linear functions and the multi-step backward Euler method is used for the discretisation with respect to time. The resulting discrete evolution model for the concentration is (17) where is the discretised concentration at time t. Assuming that the mean velocity field and the diffusion coefficient κ do not vary over time, the state transition matrix is time-independent. The vector u_t denotes the flow rates of injectors (mol s⁻¹) over the time interval [t,t+1], and the matrix is the discrete counterpart of the mapping Λ. The vector is due to the deterministic input in equation (16) during the time interval [t,t+1]. The random zero-mean Gaussian state noise process consists of two parts. The first part is due to the stochastic input term η(x,t) of the unknown boundary data in equation (16). The second part is a white noise process that approximates the inaccuracies in the CD model. The derivation of the covariance matrix of the state noise w_t is discussed in detail in 14. The most important issue is that turns out to be far from the standard ad hoc choice β_wI where β_w is the variance of the evolution errors. Such a choice would render the state estimation approach infeasible. Since the input concentration c_in(x,t) is the main source of uncertainty in the evolution model, the variance of the state noise w_t is highest on the input boundary A_in.

4. State estimation and LQG control

In this section, a model-based control strategy for regulating the concentration of a substance in a fluid is introduced. The basis of designing the control strategy is the state space representation (18) (19) where (18) is the state evolution model and (19) is the observation model. In this article (18) is the CD model introduced in section 3 and (19) is the linearised forward model of EIT discussed in section 2. The state and measurement noises are both assumed to be zero-mean Gaussian random variables with known covariances Γ_wt and Γ_vt. They are also taken to be uncorrelated so that E[v_tw_t+τ]=0 for all τ. The finite dimensional approximation of the output concentration (11) (20) is only defined at the FEM nodes over the boundary A_out. The matrix C is a restriction matrix from Ω→A_out.

The solution of the presented optimal control problem consists of two steps. Firstly, the concentration distribution in the pipe has to be estimated based on the EIT measurements and the state space model (18)–(19). In this article, the state estimation problem is solved with the Kalman filter that is particularly suitable for real-time control systems. Secondly, the flow rates of injectors have to be determined so that the concentration distribution is regulated. The optimal values for the control inputs are obtained with the LQG controller based on the estimated concentration. The state estimation problem is considered in section 4.1, and the LQG controller is introduced in section 4.2. In section 4.3, the optimal injector setting is discussed.

4.1. State estimation

The objective in state estimation is to compute the conditional expectation of the state c_t based on the measurements. In the case of real-time estimation required in real-time feedback control systems, a set of available observations at time t is {V_k,k=1, …,t}. Thus, the optimal estimate for c_t is (21) In the case of linear evolution and observation models, the approximate conditional expectation c_t|t can be computed recursively using the Kalman filter 30 (22) (23) (24) (25) (26) where c_t|t−1 is called the predictor of the state at time t and G_t is referred to as the Kalman gain. The matrices Γ_t|t and Γ_t|t−1 are the covariances of the estimate and the predictor, respectively. Note that at time t the computation of c_t|t−1 requires the control input u_t−1 which is obtained based on c_t−1|t−1. The computation of the control input u_t−1 is considered in section 4.2. For more discussion of the state estimation in the field of inverse problems, see 31.

4.2. Linear quadratic Gaussian controller

The next task is to compute the control inputs u_t required to regulate the concentration distribution on the output boundary A_out utilising the LQG controller described, for example, in 32 and 33. The computation is based on the estimated concentration distribution c_t|t. The objective is to find the control inputs u_t that minimise the difference between the output concentration y_t and a reference state r_t that is the desired profile over A_out. In this case, the reference state is a time-independent uniform vector r.

When formulating the solution to the associated LQG control problem, there are three issues to take into account. Firstly, the reference state r is non-zero contrary to the assumption that the use of a standard LQG controller would necessitate. Secondly, there is an additional source term s_t in the evolution equation (18) describing the process input. Lastly, the constraint has to be valid for all t and j=1, …,K since the injectors can only add more substance into the fluid.

Let (27) (28) (29) denote perturbation variables. In (2729), u* is the steady rates of injectors required to achieve a steady state response c* so that y* = Cc* equals r. The concentration , the control input , and the output concentration refer to perturbations from the steady state.

The steady state values of the controller are defined as (30) (31) where s* is a time-independent approximation of the process input. If s_t is considered as a random process whose distribution is known, then s* can be set to E[s_t]. Eliminating c* from equations (30) and (31) leads to (32) As the objective is to determine u* so that y* equals r, the minimisation problem (33) is considered subject to the constraint u*(j)≥0 for all j. For the non-negativity constraint to be valid, the minimisation problem is solved with non-negative least squares estimation 34. Substituting u* into (30) yields c*.

In terms of the perturbation variables, the objective of the controller is to determine that bring from its initial state to zero as quickly as possible and hold close to zero in the presence of the process input s_t and disturbance w_t. In LQG control, the optimal values of control input are obtained by minimising the quadratic average cost functional (34) where the weighting matrices Q_y=q_cI and R=r_cI are symmetric, diagonal and positive-definite. The time index t_f denotes the final time. The feasible weighting matrices for this example are discussed in 17.

The solution to the LQG optimal control problem is the state feedback control law 32 (35) where the discrete-time steady-state feedback gain K is of the form (36) The matrix S is the steady-state solution to the discrete-time matrix Riccati equation (37) where S_tf is known and Q=C^TQ_yC is positive-semidefinite. In the steady state, S_t+1=S_t=S, and S is obtained by solving (37) backward in time from a final condition 32.

Substituting the perturbation variables (27) and (28) into the control law (35) yields the actual control inputs (38) (39) The control inputs u_t could be computed from the control law (38) if the entire state c_t was known. However, because only indirect state information is obtained from the noisy EIT measurements, state estimation is needed. Therefore, in (39) the concentration c_t is replaced with the estimate c_t|t obtained in the previous section 33.

4.3. Optimal injector setting

Control performance of the system is evaluated with two criteria. First, a function (40) is considered as a measure of the output error. Second, the cost function (34) is computed. It is noted that the distance between the injectors and the output boundary A_out affects the time required for the controller to bring the output concentration from its initial state close to the reference state. Thus, the closer the injectors are to the output boundary the shorter is the initial transient and the smaller the cost. Therefore, the first time instances are excluded from the evaluations in order to eliminate the error due to the different transient performance. This is reasonable since if a control system is designed to operate for a long time period, the first time instances are irrelevant. It is worth noticing that in the cost function (34) a penalty is imposed on both the use of excessive control inputs which may exceed the operating rate of the injectors and the output error. With the choice of the weighting matrices in (34) the ratio in which the control inputs and the output error are penalised can be adjusted.

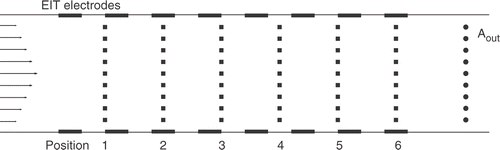
The effect of injector location on control performance is studied with a set of simulations. Six different locations for the injectors are considered as illustrated in figure 2. Locating the injectors in a straight vertical line is reasonable, since it is unnecessary to use consecutive injectors in the direction of the flow.

Figure 2. The considered injector positions in the pipe segment.

The maximum number of injectors in this example is chosen to be nine based on the physical characteristics of the system. It is important to determine if adequate control performance can be achieved with fewer than nine injectors. The set of selected injector number to be tested is N_K={1,3,5,7,9}. The single injector is situated in the middle of the pipe. Injectors are added symmetrically in a vertical line around the single injector. The control performance is evaluated for every position illustrated in figure 2 and for all the number of injectors K∈N_K.

5. Numerical simulations

In the 2D simulations, a finite segment of a pipe illustrated in figure 1 is considered. The concentration in the pipe is modelled with the CD equation (9), and the evolution is computed using the the discrete evolution model (17). In this article, the flow is approximated with a laminar flow and the velocity field in the CD equation is taken to be parabolic. The parabolic velocity field is known to be the solution of the incompressible Navier–Stokes equations in the case that the fluid is moving in a straight pipe under the influence of a constant pressure gradient 35. For an example of a more complex setting, see 14.

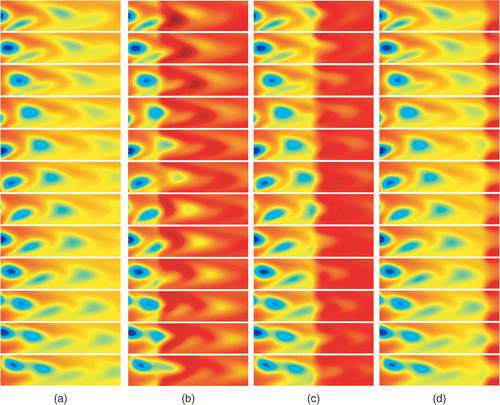
The inhomogeneities in the flow are mainly due to low concentration inclusions in a homogeneous background. The inclusions enter the pipe through the input boundary. A suitable amount of strong concentrate is injected into the flow to compensate for the inclusions as they pass the injectors. The inclusions shown in figure 3 are modelled with the input concentration . Dark blue indicates low and dark red high concentration in figure 3. Time evolves from right to left. When computing the concentration evolution, the input concentration is assumed to be known.

Figure 3. The input concentration. Time evolves from right to left.

The EIT measurements are obtained at discrete times and the time difference between the measurements is typically 50 ms. The concentration varies during the time between the consecutive measurements (current injections) due to the flow. By contrast, all the voltage observations of each current injection are made simultaneously and (approximately) instantly, so that the concentration is non-varying during each current injection. The EIT observations are modelled with the complete electrode model (16). The voltages corresponding to 64 current injections are computed using the observation model (8). Zero-mean Gaussian observation noise is added to the computed voltages. The noise consists of two parts. First, noise with standard deviation of 1% of the value of an individual observation is added to that observation. Second, noise with standard deviation of 1% of the maximum voltage is added to all observations. This is more or less a standard error model of practical measurement systems. For more information on the measurement set-up of the presented application, see 17.

At the measurement times the concentration distribution is estimated based on the voltage observations and the state space representation (18)–(19) using the Kalman filter. When constructing the evolution model for the state estimation, the velocity field and the diffusion coefficient are assumed to be known without error. By contrast, the input concentration is unknown. Therefore, the process input s_t that is due to the input concentration is approximated with the best constant estimate when computing the state estimates and the control inputs. The flow rates of injectors u_t based on the estimated concentration remain constant over the time interval [t, t+1].

The effect of control on the process in general is shown in figure 4. The uncontrolled concentration evolution in figure 4(a) is computed only for comparison. When computing the uncontrolled evolution, the control input u_t=0. In figure 4(b) nine injectors are in position 1, in figure 4(c) in position 3, and in figure 4(d) in position 6. Due to the control, the concentration over the output boundary A_out is regulated and it matches to a desired level. Especially, when the injectors are in position 3, the control system works very well.

Figure 4. (a) The uncontrolled concentration evolution. (b) The controlled concentration evolution when the injectors are in position 1. (c) The controlled concentration evolution when the injectors are in position 3. (d) The controlled concentration evolution when the injectors are in position 6.

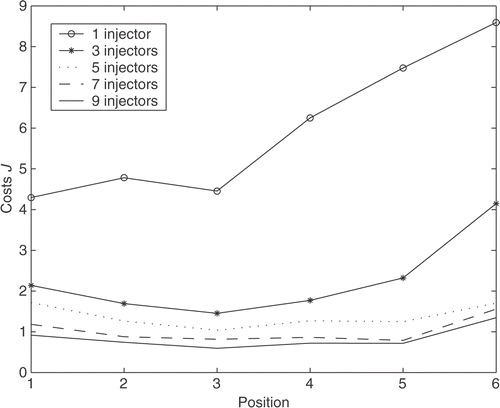
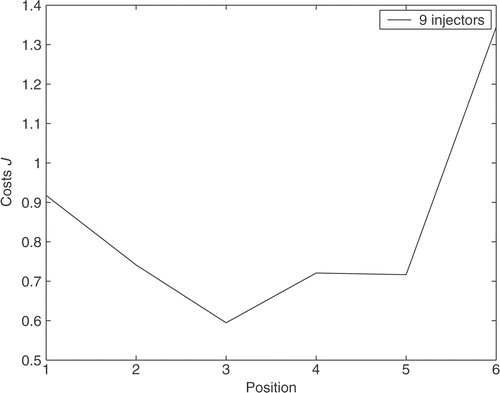
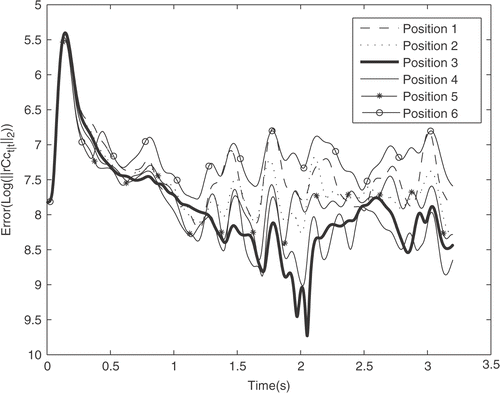
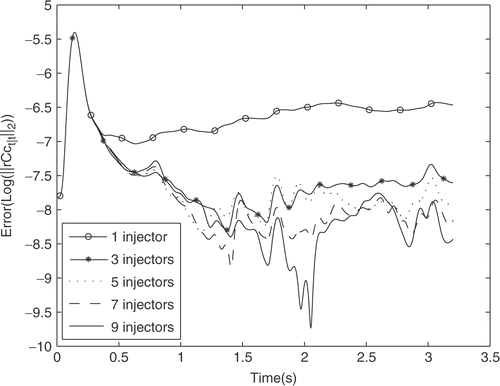
The costs J for different injector locations and number of injectors are computed and plotted in figure 5. In this case, the optimal injector setting is based on minimising both the output error and the amount of injected concentrate according to the selection of the weighting matrices. The smallest costs are obtained with nine injectors, and the costs increase as the number of injectors decreases. However, with seven injectors the results are essentially as good as with nine injectors. In figure 6, the case in which nine injectors are used is considered in detail. The costs for different injector positions are plotted. It can be concluded that the optimal injector position is position 3 when inspecting the cost function. It is evident that even a small change in the injector position can cause a significant decrease in the cost function.

Figure 5. The costs J for different injector positions and number of injectors.

Figure 6. The costs J for injector positions when nine injectors are used.

Excluding the control inputs from the consideration, the output errors for the different locations when nine injectors are used are plotted in figure 7. The logarithmic scale is used for visual reasons. The injector positions 3 and 4 have the smallest output errors at all times after the initial transient. The difference between the output errors of positions 3 and 4 is insignificant. Therefore, if the control performance is evaluated only based on the output error, a more specific inspection around the positions 3 and 4 is unnecessary as the improvements in control performance would be insignificantly small. However, when inspecting the cost function, the optimal position was shown to be position 3. The output errors for different injector number are depicted in figure 8 when the injectors are in position 3. Similarly to the consideration of the cost function, the smallest output errors are achieved with nine injectors. The result in this example is obvious since it is difficult to obtain a smooth output concentration profile with only a few injectors despite the diffusion property of the process. However, the output errors for seven injectors are almost as small as for nine injectors. In this case, therefore, the improvements that are obtained by adding more injectors are often of little consequence in comparison to the expenses required in practical examples.

Figure 7. The output errors for different injector positions when nine injectors are used.

Figure 8. The output errors for different injector numbers when the injectors are in position 3.

In this specific example it can be concluded from the numerical simulations that there are three issues affecting the optimal actuator setting. First, by locating the injectors in the region in which the state estimation accuracy is as high as possible, the control performance can be improved. The conclusion is evident, since bias in the state estimates creates bias to the optimal control inputs, that in turn results in inadequate concentration distribution on the output boundary A_out. The state estimation accuracy can be deduced, for example, by inspecting the mean state noise variance, that is, time-averaged diagonals of the state estimate covariance. By considering the physical characteristics of the process, it can be stated that the sensing system cannot observe the concentration in regions upstream of the first and downstream of the last EIT electrode pair. Naturally, the concentration in those regions can be estimated but unexpected disturbances or modelling errors may occur. In addition, the uncertainty of the state estimates very near the input boundary A_in is typically high, because the input concentration is the primary unknown of the system. Therefore, it can be concluded that in this example the state estimation accuracy is high in the middle of the pipe.

Second, by finding the optimal injector setting the homogenising effect of diffusion can be fully exploited. As the injected concentrate is distributed to a small volume only, it is impossible to obtain a uniform or even a smooth concentration distribution with just a few injectors if the injectors are too close to the output boundary A_out. Once the injectors are located further from the output boundary A_out, the injected concentrate is diffused better. Also, the state estimation accuracy near the output boundary A_out is often lower than in the middle of the pipe.

Third, the injectors can only add concentrate into the flow and cannot extract anything away from the pipe. Therefore, the operating point of the system has to be set so that it should be very unlikely that reduction of the concentration (negative controls) is necessary. Since in this example the operating point is after the main mixer, the fluctuations in the concentration should be relatively small. Therefore, the control system works well even when reduction of concentration is impossible.

6. Conclusion

In this article, it is shown that finding the optimal actuator setting can improve significantly the control performance of an industrial process. Often in complicated processes with sophisticated geometries and multiphased flows, decision-making about the actuator setting based on intuition can lead to ineffective control systems. Therefore, numerical simulations can provide valuable information about the optimal actuator locations and the adequate number of actuators to be taken into account in control system design. From the simulations it can also be concluded that the state estimation accuracy and the homogenising effect of diffusion are closely related to the optimal actuator setting in CD processes. Although the example presented in this article concerns controlling concentration in a fluid, the approach is applicable to other imaging modalities and industrial processes.