Inverse problems in space science and technology

Abstract

Solutions for inverse problems appearing in space applications and space technology are described. The inverse problem is formulated as a nonlinear optimization problem. Usually some additional information must be added from our previous knowledge about the physical phenomenon. In general this a priori information means smoothness, in other words, regularized solutions are searched for. The methodology is applied to geophysics (magneto-telluric inversion), meteorology (temperature retrieval from satellite data), and oceanography (inverse hydrologic optics), as examples of space applications. The scheme is also employed for solving an inverse problem emerging from technology: the inverse design of a space radiator.

Keywords:

• Space research
• inverse problems
• entropic regularization
• extremal optimization
• genetic algorithm

1. Introduction

This study is focused on the application of inverse problem methodology for solving some problems that have emerged in space science and technology, as well as in space applications. It represents a survey of some results obtained by scientific research groups from the National Institute for Space Research (INPE, Brazil), and addresses future research in such subjects.

The inverse problem methodology is an implicit technique for parameter and/or function estimation. The algorithm is formulated as a constrained nonlinear optimization problem, in which the direct problem is iteratively solved for successive approximations of the unknown parameters. Iteration proceeds until an objective-function, representing the least-square fit of the results of the model and of the experimental data added to a regularization term, attains a specified small value.

2. Formulation of the inverse problem

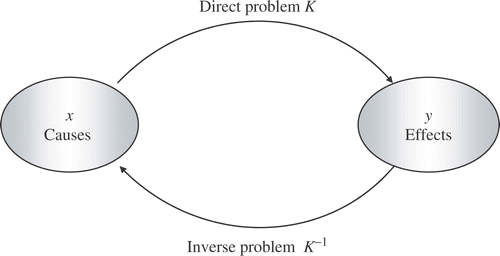
A quotation attributed to Prof. Oleg Mikailivitch Alifanov, a great Russian proponent of Inverse Methods, says: “Solution of an inverse problem entails determining unknown causes based on observation of their effects”. On the contrary, the corresponding direct problem involves finding effects based on a complete and precise description of their causes. Figure 1 displays a graphical representation of the concepts mentioned above.

Figure 1. Representation of the direct or forward (given x, find y = K(x)) and of inverse problems (given y, find x = K⁻¹ (y)).

The solution for an inverse problem can be searched formulating it as an optimization problem. A technique for property reconstruction from measurements can be described as a generalized least squares approximation. The standard least squares solution can guarantee the existence of a solution, but it can be unstable in the presence of noise, a permanent feature in experimental data. Inverse problems belong to the class of ill-posed problems, in the sense that the existence, uniqueness and stability of the solutions cannot be assured. In order to have a well-posed inverse problem, assuring a final solution that is stable and physically acceptable, some a priori information must be added to the quadratic difference term. In general, this additional information associated to the inverse solution means smoothness.

Denoting by , the unknown vector to be determined by the inverse analysis, the inverse problem can be formulated as a nonlinear constrained minimization problem, (1) where N_p denotes the number of unknown parameters, the lower and upper bounds l_q and u_q are chosen in order to allow the inversion to lie within some known physical limits, and the objective function is given by (2) where N_m denotes the number of measurement points (or points for comparison), Ω[p] the regularization operator, and Φ a quantity that can be measured and modeled in a mathematical formulation.

There are two formulations for solving inverse problems 3 (see also: 58 – section: Inverse Problem). The unknown function can be solved in a parameter estimation approach, or a function estimation approach, where the functional form is not available.

In the absence of an explicit solution, the optimization problem defined by equation (1) must be iteratively solved by an optimization algorithm. These algorithms can be classified as: deterministic search procedures, such as the steepest descent, Newton method, variable metric methods, conjugate gradient 27; and stochastic search procedures, such as genetic algorithms 19, and simulated annealing 24.

According to Tikhonov and Arsenin 55, ill-posed problems can yield stable solutions if sufficient a priori information about the true solution is available. Such information is added to the least squares approximation by means of a regularization term, in order to complete the solution for the inverse problem.

Some regularization functionals are described on later. However, it is useful to mention that some of the optimization methods themselves, present filtering properties, as the steepest descent, Landweber, and conjugate gradient 5. The Levenberg–Marquardt method is one of them, and it is commented on later. Other regularizations could also be used, as the truncated singular value decomposition 5, 33, but here we focus on the regularization operators used in our study.

2.1. Tikhonov regularization

A well-known regularization technique proposed by Tikhonov 55 can be expressed by (3) where p^(k) k-th derivative (difference), and the parameters α_k ≥ 0. In this work, if α_k = δ_kj (Kronecker's delta), i.e., then the method is called the Tikhonov regularization of order-j (Tikhonov-j). In particular, the Tikhonov regularization of order zero is referred to just as Tikhonov regularization.

2.2. Entropic regularization

The maximum entropy principle was first proposed by Jaynes 23 on the basis of Shannon's information theory 45. Similar to the Tikhonov's approach, this general inference method searches a global regularity, yielding the smoothest solution which is consistent with the available data.

Recently, a higher order entropic regularization has been proposed 6, 7, 33, 41, 42. A generic expression for entropic regularization can be written as (4) where (5) and represents the m-th difference among the vector of the parameters. For example, the first three differences are: (6) Here ς, a small positive constant, assures that entropies of higher order will always have a positive value. The function S^m attains its global maximum when all the r_q are the same, i.e., a uniform distribution with S_max = log N_q (here ς = 0); in contrast, the lowest entropy value S_min = 0 is reached when all the elements r_q but one are set to zero. It can be shown that the Morozov's discrepancy principle can also be applied to the maximum entropy (MaxEnt) regularization of higher order 33.

2.3. Solving optimization problem

Several optimizers can be used to compute a solution of such problems. The methods can be classified as deterministic or stochastic strategies. Two deterministic schemes have been employed in our studies: Levenberg–Marquardt 22 and quasi-Newton 34 methods. Three different stochastic schemes are used: genetic algorithm, simulated annealing, and extremal optimization.

2.3.1. A quasi-Newton method

The optimization problem is iteratively solved by the quasi-Newtonian optimizer routine from the NAG Fortran Library 34–routine E04UCF.

This algorithm is designed to minimize an arbitrary smooth function subject to constraints (simple bound, linear or nonlinear constraints), using a sequential programming method. This routine has been successfully used in several previous works: in geophysics, hydrologic optics, and meteorology.

2.3.2. Levenberg–Marquardt method

The Newton's optimization method has quadratic convergence, but it is strongly dependent on the initial guess. However, the steepest descent method is more robust than the Newton scheme, but it presents a slower convergence than Newton method. The idea to combine the robustness of the steepest descent method with the convergence speed of the Newton method is applied by the Levenberg–Marquardt (LM) procedure 25, 28, as follows: (7) where n denotes the iteration step, J ≡ ∂Φ^Mod (p)/∂p, and η is the damping factor.

A regularization property emerges from the addition of the identity matrix (I) multiplied by a dynamical parameter ηⁿ, whose value is changed in each iteration step, to the term J^tJ. The addition of the identity matrix makes the LM-method similar to the Tikhonov regularization.

The algorithm is implemented in the IMSL 22 library–routine DBCLSF.

2.3.3. Genetic algorithms

Genetic algorithms (GA) are essentially optimization algorithms whose solutions evolve somehow from the science of genetics and the processes of natural selection–the Darwinian principle. The most important phases in standard GAs are selection (competition), reproduction, mutation and fitness evaluation. Selection is an operation used to decide which individuals to use for reproduction and mutation in order to produce new search points. Reproduction or crossover is the process by which the genetic material from two parent individuals is combined to obtain one or more offsprings. Mutation is normally applied to one individual in order to produce a new version of it where some of the original genetic material has been randomly changed. Fitness evaluation is the step in which the quality of an individual is assessed.

Metacode of a possible GA implementation is as follows:t = 0;Initialization Pop(t);Test Pop(t);While (no end) t = t + 1; Select Pop(t) from Pop(t − 1); Change Pop(t); (crossover and mutation) Test Pop(t);End

2.3.4. Simulated annealing

The Simulated annealing (SA) method is inspired by a physical process of slow cooling of initially melted material. This process looks for obtaining perfect crystals which, at the end of cooling, have the smallest possible internal energy. In the process of cooling the molecules move into the interior of the mixture randomly, positioning themselves in a crystal network when the temperature is reduced. The search in the SA algorithm is initiated in some point of the search space. The method uses the Metropolis’ algorithm 30, 40.

Steps for SA implementation 40 are as follows:

a.	Define initial candidates, and compute for each one its objective function value. Define an initial temperature for the problem.
b.	Chose new candidates randomly (if they have the same value for the mathematical model, choose others). Re-compute for each one the objective function.
c.	If the value of the objective function decreases between two consecutive iterations the changing is accepted, and the process continues. If the value is greater, the changing is accepted with probability Pr = e−(ΔU/T), where ΔU is the difference between the value of the objective function between two iterations.
d.	Decrease the temperature to r*T (annealing schedule) after a certain number of iterations of step (b). Here T is the temperature in the step (c), and r is a reduction factor.
e.	Repeat steps b–c–d up to the convergence.

2.3.5. Extreme optimization

Extreme optimization (EO) is a new optimization method based on the concept of co-evolution natural selection to obtain an optimal solution 4. The method is based on an evolution model, in which some characteristics of self-organizing criticality are present 1. Although it is an evolutionary method, unlike the GA, there is no genetic codification of population in the EO.

Steps for EO implementation 50 are as follows:

a.	Define initial candidates.
b.	In this step an adaptive index is associated to candidate solution.
c.	The less adapted element, obtained in the previous step, is changed with another element in a random way. In another approach, that we will call hereafter EOmod, two elements are chosen for being exchanged with probability , where n is an adaptability index, ranging from 1, for the less adapted element, up to N, the maximum number of elements–the exponent is an adjustable parameter. With this probability distribution, even well adapted elements can be chosen for the exchange.
d.	Repeat steps b–c up to the convergence.

3. Applications

3.1. Magneto-telluric inversion

The magneto-telluric inversion is a geophysical inverse problem: the use of electromagnetic fields induced by natural sources in the ionosphere and magnetosphere to determine the electrical conductivity of the earth's subsurface. Appearing in various areas such as petroleum prospection, mining and search for ground water, it has special relevance in the exploration of regions which are difficult to probe with conventional seismic methods.

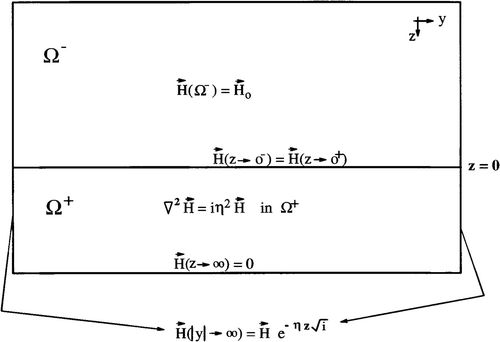
The forward problem is modeled using 2D Maxwell's equations for calculating the electromagnetic fields, and the problem is outlined in figure 2. Two regions can be visualized from this figure: Ω⁻ representing the atmosphere, and Ω⁺ a region inside the Earth. In the atmosphere, the geomagnetic field H is constant, but into the Earth the field H obeys a Poisson equation (for details see 6, 41, with η = 4πωσ–being σ = (y, z) the electric conductivity and ω the electromagnetic wave frequency. The boundary conditions are also shown in figure 2.

Figure 2. Diagram for showing physical problem in magneto-telluric inverse problem.

For solving this inverse problem, the first-order minimum entropy regularization method (MinEnt-1), second line of equation (6), was employed over 2D earth models, using synthetic data with 1% of noise 6, 41. The objective function is expressed by (8) Results are presented in the form of two-dimensional conductivity maps in logarithmic scale (figure 3). The unknown conductivity values are shown in the two-dimensional maps. The leftmost column (boundary condition) and the topmost row (earth's surface) are assumed to be known and, therefore, were left out of the inversion procedure. Figure 3(a) is the true model used to generate the synthetic data. Figure 3(b) is the inversion obtained without regularization, and figure 3(c) and (d) is the inverse solution computed from MinEnt-1 (γ₀ = 0) and MaxEnt-0 (γ₁ = 0), respectively.

Figure 3. Earth models for magneto-telluric inversion using entropic regularization.

The optimization problem (8) has been solved using a quasi-Newton method 34 and a genetic algorithm 35, 36, 38.

3.2. Hydrologic optics

There are two physical descriptions for light transmission: (i) from electromagnetism theory, where the light is thought of as a wave; (ii) from linear non-charged particle transport theory, if the light is understood as a beam of particles (photons). The second approach is considered here. 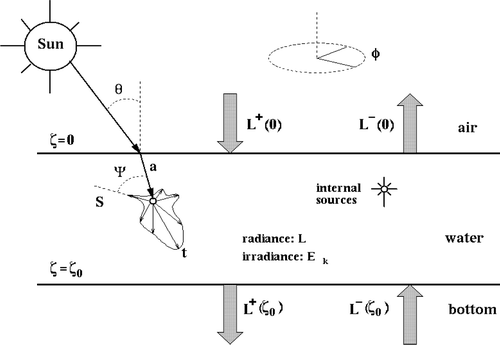The linearized Boltzmann equation, known also as transport equation or radiative transfer equation, for a given wavelength, λ, describes the photon distribution, given by 17 (9) where L denotes the radiance, β the scattering phase function, ϖ₀ = b/c the single scattering albedo, c = a + b the beam attenuation coefficient, a and b the absorption and scattering coefficients, respectively, ζ is the optical depth, ξ′(θ′, φ′) and ξ(θ, φ) are the incident and scattered directions for an infinitesimal beam, θ is the polar angle, φ is the azimuthal angle, S is the source term, and μ = cos(θ). An outline of the physical process is depicted in figure 4.

Figure 4. Pictorical representation of the direct radiative problem.

In our studies the following three techniques have been applied to solve the forward problem:

	Invariant Imbedding: This method is used in the Hydrolight 3.0 computer code, and its description can be found in Mobley 32. In this approach, the linear two-point boundary problem is transformed into a nonlinear initial value problem (matrix Ricatti equation), solved by a well-established integrator. The Hydrolight software allows the choice of many types of internal source terms and different weather conditions.
	Analytical SN method: First, the radiance is split up into unscattered and scattered components. The solution for the former component is given by a simple expression, and the scattered radiance is expanded by elementary solutions of the discrete ordinate equations. The coefficients of the expansion are obtained by solving a linear algebraic equation. Full presentation of the method is done by Chalhoub and Garcia 11.
	LTSN method: This scheme appeared in the early nineties in the neutron transport context 2, 57, and was then extended to radiative transfer problems 44. A description of the method and its innovations were expressed by Segatto and Vilhena 44. The convergence of the LTSN method was established using the C0-semi group theory 39.

A comparison, among different methods for solving equation (8), was carried out by Chalhoub et al. 16, while the performance for the three methods mentioned above in the parallel computer environment was analyzed by Souto et al. 48.

The development of inversion methodologies for radiative transfer problems has been an important research topic in many branches of science and engineering 21, 29. Some results obtained with the application of the inverse methodology presented in section 2 are discussed. For details, please refer to the corresponding papers. The properties of interest in hydrologic optics are: internal source term, inherent optical properties (IOP: absorption and scattering coefficients, phase function), and boundary conditions.

Reconstructions were obtained using in situ radiometric data and remote sensing data. Estimations obtained with the present inverse analysis are summarized in table 1, showing the property estimated, forward technique, regularization operator, and optimizer used.

Table 1. Estimation of properties in hydrologic optics

Cases	Property	Direct problem	Optimizer	Regularization
1	S(ζ)	Imbedding	Q-Newton (NAG)/GA	No
2	S(ζ), a, b	Imbedding	Q-Newton (NAG)	MaxEnt-0
3	β(ξ)	Standard SN	Q-Newton (NAG)	MaxEnt-0
4	B.C.	LTSN	Q-Newton (NAG)	Tikhonov-0
5	β (ξ), ϖ0	ASN	L–M (IMSL)	L–M method
6	β (ξ), ϖ0, τ0	ASN	L–M (IMSL)	L–M method
7	S(ζ)	SN–multispectral	L–M (IMSL)	L–M method

An interesting aspect in case 1 is that no regularization was necessary 53, and the source term is approximated as the sum of Gaussian distributions with standard deviation σ = 0.75. In case 2 the alternate step-by-step strategy was introduced, meaning that a, b coefficients are estimated first, then the source term is estimated, and finally the convergence is checked. This is only parameter estimation, because there is no dependence on the depth of the coefficients a, b 54. The phase function was identified in cases 3 and 4 12, 13, where the retrieval was possible even with high level of noise. Boundary conditions are identified in case 5 43; see also 8, 9. A joint estimation of high scattering order phase function, single albedo, and optical thickness were identified in case 6 14. Finally, case 7 represents our first result in inverse hydrologic optics using remote sensing data 15.

3.3. Atmospheric temperature profile from satellite data

Considering the infrared radiances captured by the satellite, the integral form of the radiative transfer, for a given wavelength λ, can be simplified for the following expression 26: (10) where I_λ(τ_λ) is the radiance at height z, τ_λ and are the transmittance at level z and at surface, and B_λ is the Planck function 26: (11) where h being the Planck constant, c the light speed, k_B the Boltzmann constant, and T the temperature at level z.

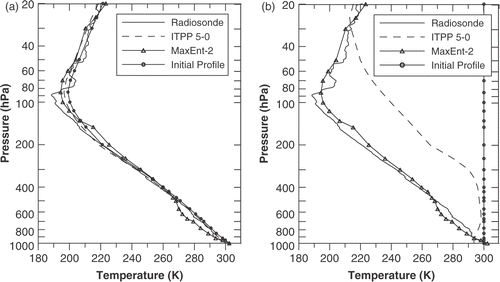
This inverse problem was solved using seven satellite channels for retrieving the atmospheric temperature profile with 40 layers. The second-order maximum entropy principle was used as regularization 10, 42. Results are shown in figure 5. Our methodology has shown to be more robust than ITPP-5 code 37, since it produces the same result for different initial guesses (figure 5a and b), and it obtained the best agreement with minimum temperature around the pressure 100 hPa.

Figure 5. Atmospheric temperature profile for different first guess: (a) climate data base; (b) homogeneous atmospheric layer.

3.4. Space radiator design

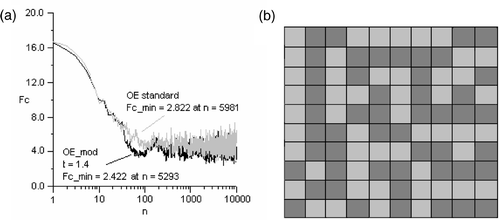
The space radiator is a device used to efficiently put out excessive heat from within the satellite or space station to the outer space. Its function is essential for thermal control for any space vehicle. In general, the radiator consists of parts of the satellite external surface, where special dye or strip with specific thermo-optics properties is applied. The area and the number of radiators can change, depending on the satellite size. However, the radiator can also be made independently of the space vehicle structure, such as for the International Space Station. Here, the designer searches for a suitable combination of paints or adhesive strips for covering different areas of the radiator, in such a way that effective emissivity obtained from this arrangement would be close to that designed one. The effective emissivity obtained using EO approach 50 is shown in figure 6.

Figure 6. (a) Population evolution of emissivities for the EO iterations. Fc represents the value of the objective function for the radiator; (b) configuration with the smallest value by the modified EO for the objective function.

4. Final remarks

A methodology for inverse problems appearing on space applications has been presented and applied, mainly dealing with regularized solutions. Local and global searching strategies have been efficiently employed for solving the inverse model. One important remark is to point out that EO algorithm has been generalized and applied to heat pipe and airfoil design 51, 52. In addition, other implementations of the optimization algorithms worked here can also be investigated, such as the SA algorithm (see for example 20).

Future works can be listed as follows:

•	The multi-spectral reconstruction in hydrologic optics needs more studies.
•	New regularization operators, such as non-extensive entropy 46, 56, should be investigated for problems worked here.
•	New approaches deserve to be explored, such as neural networks 47, Kalman filter, and variational methods 18.
•	New applications, for example: vibration in aero-space structures, pollutant atmospheric source identification, observational cosmology (for e.g., from background cosmic radiation in microwaves, two inverse problems emerge: computing the cosmic temperature variation, and the sky maps, represented the coefficients of the spherical harmonic expansion of the sky temperature, see 59).

Acknowledgements

This work was partially supported by FAPESP and CNPq, Brazilian agencies for research support.