Projected Barzilai–Borwein method for large-scale nonnegative image restoration

Abstract

Image restoration refers to minimizing the degradation caused by the sensor environment, such as misfocused CCD cameras, nonuniform motions, atmospheric aerosols, and atmospheric turbulences. In image restoration problems, it is reasonable to add nonnegative constraints because of the physical meaning of the image. Then, the problem can be expressed as a quadratic programming problem with nonnegative constraints. However, in previous research, a parameterization technique is needed to reduce the problem into an unconstrained optimization problem. To avoid parameterization techniques, we apply the recently developed projected Barzilai–Borwein (PBB) method to solve this quadratic programming problem. Also, a novel approach for reducing the cost of matrix-vector multiplication is proposed when applying BB and PBB methods for atmospheric image restoration. The numerical experiments show that this method is promising for large-scale image restoration problems.

Keywords:

• 65J10
• 65K10
• 65F22

1. Introduction

Image restoration is a major problem in digital image processing, which has been attracting increasing attention from different research fields in recent years. Image restoration refers to the restoration of degradation which may be caused by senor noise, misfocused CCD cameras, nonuniform motion, atmospheric aerosols, or random atmospheric turbulences. For example, in remote sensing applications, we are often required to recover the true signal or image f with resolution N  × N by direct ground measurements or by the data from satellite sensors, and then giving the information about the modulation transfer function (MTF) or the point spread function (PSF) of the system. The perfect case for the PSF of the sensor should be a Gaussian distribution. A key problem in image restoration is to restore the image by solving a blurring model and removing noise. This is because transferring the reflected signal from the land surface to the satellite sensors inevitably encounters interference from the atmosphere, such as atmospheric turbulences and aerosols. This interference also leads to the blurring of the original signal.

Astronomical images are usually corrupted or distorted by blurring and noise. The blurring is characterized by a PSF or impulse response, while the noise is usually assumed to be additive, similar to Gaussian random noise, Poisson noise or background noise. The power distribution in the image plane due to a point source in the object plane can be described by: (1) where, h(x, y) is assumed to be the true image; h_δ(x,y) denotes the recorded blurred image; f(x, y) denotes the original object; k(x, y) is the 2D PSF describing the object's unique relation in the spatial domain;  ☆ is the convolution operator; x and y are the spatial coordinates; and, n(x, y) denotes an additive noise term. The above expression is commonly modeled as a first-kind integral equation of the form (2) The image restoration problem recovers f according to the knowledge of h_δ and k.

In digital image restoration, a discrete model of (1.2) is necessary. The discretization can be performed by a discrete quadrature rule, such as a midpoint quadrature method and a rectangular quadrature method. We will not discuss the discretization in detail, but instead assume that after discretization, we obtain the following linear system: (3) where , . The noise n cannot be ignored and the matrix is usually badly conditioned, so we cannot easily solve this linear system algebraically.

In practice, the vector f records the image pixel values, so the components of f must be nonnegative. Thus, we can express the image restoration problem as (4) The remaining task is to approximately solve (1.4) efficiently. It is clear that (1.4) is equivalent to a constrained convex quadratic programming problem (5) where . There are many methods by which we can solve the convex quadratic programming problem, but we prefer the BB method which has been shown to converge rapidly in many situations.

The BB method was first proposed by Barzilai and Borwein 2 for solving the unconstrained optimization problem (6) where . The method is valid for strongly convex quadratic programming with m variables (7) where is a symmetric positive definite matrix. Let x_k be the k-th iterate and g_k the gradient of q at x_k, given by (8) A gradient method for solving (1.7) calculates the next point from (9) where α_k is the stepsize that depends on the method being used. For example, for the classical steepest descent (SD) method 6,32, the stepsize α_k is chosen such that q(x) is minimized along the line , that is, (10) The key point of Barzilai and Borwein's method is the two choices of the stepsize α_k (11) and (12) which is based on the investigation of the quasi-Newton equation of (1.7), i.e., (13) where y_k = g_k + 1 − g_k, s_k = x_k + 1 − x_k. Replacing A by a diagonal matrix (α > 0) and solving yields (14) Similarly, if we use αI to approximate the inverse of A, we can choose α_k as the solution of problem and obtain (15) Note that and y_k − 1 = As_k − 1, and hence, the equivalent form (1.11) and (1.12) are deduced.

Note that the BB method does not enforce the nonnegative constraints. However, the image pixels are always nonnegative, that is, . Therefore, in order to apply the BB method to solve (1.5), the projection of the iterates to an appropriate solution set is necessary. In this study, we solve (1.4) using an algorithm based on the PBB method, which has recently been addressed by Dai and Fletcher 4.

This article is organized as follows. In section 2, we give a brief review of the discrete ill-posedness of image restoration problems and the regularization methods for suppressing the ill-posedness. Both the methods in the spatial domain and the frequency domain are introduced. In section 3, algorithms for nonnegative image restoration are addressed. In section 4, we introduce the PBB method and its variants. In section 5, we discuss the convergence and regularizing properties of the BB and PBB methods. In section 6, a novel approach for matrix-vector multiplication (MVM) is introduced. In section 7, the numerical experiments are reported. Finally, in section 8, we present the conclusion and future works.

2. Summary of discrete ill-posedness and regularization for image restoration

In this section, we describe the ill-posed nature of the image restoration problem and summarize some developed solution methods.

The discrete ill-posedness of problem (1.3) arises from the fact that the discrete kernel is badly conditioned and the right-hand member contains noise. As a result, small perturbations in may lead to significant oscillations in the inversion result. Therefore, to stably recover the unknown, regularization is necessary. There are two ways to introduce the regularization technique. One is the frequency domain regularization, that is, we first perform a Fourier transform on both sides of (1.1) to have (16) where is the optical transfer function (OTF) in spatial frequencies ω_i and ω_j and denote the Fourier transforms of h, f and n. The OTF describes the degradation process which is determined by the focal length, optics, lenses, and temperature range. The blurred image can be restored with a restoration filter yielding the restored image (17) The restoration with the inverse filter, being the inverse of the OTF, that is, results in unlimited amplification of the response when approaches zero for high frequencies. The undesired amplification can be alleviated by using regularization, such as the Wiener filtering function 7 (18) where SNR is the signal-to-noise ratio of the image, which attenuates high noise components. Another main filtering function in the spatial domain is the Lagrangian filtering function, which is more commonly known as the Tikhonov filtering function 20 (19) where S(ω_i,ω_j) is an even function preassigned by users, which should be piecewise-continuous on every finite interval; nonnegative and greater than zero for ; greater than a positive number for sufficiently large ω_i and ω_j, and that for every α > 0. For example, we can choose S(ω_i,ω_j) to be or , where p and q are natural numbers 20,31.

The main shortcoming of the frequency domain regularization methods is the difficulty of finding the appropriate ending frequency at which the OTF will vanish quickly.

Spatial domain regularization methods is a wide research field for image restoration problems. In the spatial domain, the canonical regularization method is the Tikhonov regularization, whose standard form is (20) where is a penalty term on the unknown f. There are many tricks for choosing Γ(·). For example, the popular choice of as , which is defined as , where L is the scale operator which can be chosen as a positive definite or positive semi-definite matrix. Recently, nonsmooth regularization has received much more attention in the restoration of nonregular images, as well as in the classification and segmentation of textured images 19,24,28. The nonsmooth regularization, known as the total variation (TV)-based regularization, refers to choosing the function as the discretization of the functional Γ( f ) = ∫|∇f |, where ∇f is the gradient of f and |·| is the Euclidean norm. In (2.5), α > 0 is the so-called regularization parameter which plays a major role in regularizing the ill-posedness. The value of  α is positive and will be typically small. But the choice of an appropriate  α is a difficult thing, which is usually related to the spectrum of the discrete kernel and the unpredictable noise level in . The solution methods for (2.5) include singular value decomposition (SVD)-based direct method 10, Newton and quasi-Newton method 25, gradient methods (e.g. steepest descent (SD) method and conjugate gradient (CG) method) and various preconditioning techniques 22. CG method has proven to be an efficient iterative regularization method for recovering the correct image from its degradation 9. This method overcomes the difficulty of choosing the regularization parameter  α by controlling the iteration indices; but, the optimal stopping iteration index still depends on the noise level. Recently, a two-stage image reconstruction algorithm was proposed 11. Based on the observation of the gravitational lens system Q2237  + 0305 from Maidanak Observatory, the authors proposed a two-stage algorithm: at the first stage, the algorithm is based on the Tikhonov regularization; at the second stage, the numerical galaxy model obtained in the first stage is used for the photometric treatment of all observational data. However, this method still relies on the imposed regularized term with the regularization parameter α. The trust region method has recently proved to be another useful regularization tool for image restoration 26–30. This method involves solving a trust region subproblem in each inner iteration and accepting a new trial step within its trust region. No additional regularized term with the regularization parameter  α is imposed.

In the following context of our study, we will consider another iterative regularization method in the spatial domain, which was first addressed in optimization as the BB method 2. Considering the physical meaning of the widely used 8-bit images, the pixel value varies from 0 to 255. We then reformulate the problem by imposing the nonnegative constraints. This was already considered by several researchers, such as Bardsley and Vogel 1, Hanke et al. 8, Nagy et al. 14 and Rojas et al. 18.

3. Image restoration with nonnegative constraints

A natural way of imposing nonnegative constraints is to minimize the energy of the noise/error in the problem (1.3) subject to . The parameterization by exponential function can replace the constrained optimization problem with an unconstrained problem, which actually converts a linear transform into a nonlinear transform . For example, Nagy and Strakos 14 give a modified SD method for (1.4). In their method, they use the parameterization , i.e., and use the chain rule to find the gradient of Ψ with respect to z (21) where . Therefore, the SD method can be generated as follows (22) where is the search direction of the negative gradient. To maintain nonnegativity of the iterates f_k, the line search parameter α_k is taken to be the minimum of and (1.10) with g_k replace by d_k − 1.

Hanke et al. 8 deal with (1.3) via the Tikhonov regularization, which amounts to minimizing the functional (23) over the nonnegative quadrant . They solve (3.3) with Newton's method. Likewise, in their method, they first introduce a parameterization to transform the problem into an unconstrained problem with the variable z. Then, they apply Newton's method to solve the unconstrained problem. The gradient and the Hessian are given by (24) (25) where . For the solution of the linear subproblem, they further make an approximation of the exact Hessian by (26) After obtaining Newton's direction and stepsize γ_k, the next point f_k + 1 can be obtained by where .

Tikhonov et al. 21 apply the method of projection of CGs to the solution of ill-posed problems on the sets of special structure. In their method, instead of solving (2.5), they solve the problem of minimizing φ(x) = Ψ(Tx) on Π⁺, where Π⁺ is the set of vectors having nonnegative coordinates, T is an operator from to , which can be expressed as a linear combination of vertices of the convex bounded polyhedra and f = Tx. This method requires constructing an approximation solution of (1.3) on the set of monotone functions.

Bardsley and Vogel 1 recently addressed a gradient projection-reduced Newton-CG method to solve (3.3). They formulated the nonnegatively constrained problem by introducing a Poisson log likelihood functional. They first defined a feasible set and then a projection of a vector onto the feasible set is defined as . Their method is based on finding the active and inactive variables. In this method, each outer iteration is comprised of two stages. The first stage consists of projected gradient iterations to identify the active set, while the second stage uses conjugate gradient iterations to compute a Newton step on the inactive variables. A sparse preconditioner is also considered.

In addition, Rojas and Steihaug 18 solved the problem: (27) They formulated this problem by solving a sequential trust region subproblem, where a new technique developed for the large-scale trust-region subproblem was performed, that is, they first introduced a logarithmic barrier function, then reformulated it into a new trust region subproblems and solved it. Meanwhile, the duality gap technique is used to update the barrier parameter. Their method is actually an interior-point method, where trust region strategies are included.

Our method is different from all of the above methods. In the above methods there is either a need to impose a regularized term with the regularization parameter α, or a need to introduce a parameterization by either an exponential function, or entropy function, or logarithmic function. We prefer the PBB method for the minimization of the norm of the residual. This method solves a quadratic programming with nonnegative constraints without introducing the parameterization and the additional regularized term with the parameter α. It has been illustrated that the BB and PBB method performs well for the quadratic model in numerical optimization 4,17. So, we hope that this method will also be efficient for ill-posed inverse problems and not limited to the image restoration problem considered in this study. Details are presented in the next section.

It deserves noting that the BB and the PBB methods are essentially some kind of gradient methods. There are several gradient descent iterative methods that have been used for nonnegatively constrained image reconstruction without a regularization penalty term/parameter.

Eicke 5 proposed a projected Landweber (PLW) iteration method for convexly constrained ill-posed problems in Hilbert space, which is also addressed in 3 recently. The iteration formula reads as follows: (28) where , P_Ω(·) is the projection operator defined in section 4. The PLW method is an iterative method which can be used for approximating the solutions of the image restoration problems. Its convergence and regularization properties have been investigated in 5. However, a well-known fact is the practical difficulty of the method, i.e., the convergence is too slow. Too many iterations are required to obtain the best approximation. Therefore, if one wants to use the method, the acceleration technique must be considered although how to accelerate remains an important issue.

Similar to PLW iteration method, projected gradient (PG) method can be deduced for image restoration problem, for example, the algorithm given by Vogel 25. The iteration formula reads as follows: (29) where P_Ω(·) is the projection operator defined in section 4, is the steplength by line search. For SD method, . However, this method becomes slower as the iterations proceed, and the zigzagging phenomenon occurs 32.

Notably, for the nonparameterization algorithm, the gradient projection conjugate gradient (GPCG) for the solution of bounded constrained quadratic programming problem had been originally designed 13 for large scale problems. The GPCG algorithm uses a gradient projection method to identify a face of the feasible region Ω that contains the solution, and the CG method to search the face. We will compare the GPCG method with the BB and PBB methods for large scale image restoration problems.

4. PBB method for nonnegatively constrained image restoration

The PBB method is considered for solving box-constrained quadratic programming (BCQP) 4 (30) where is a symmetric matrix but not necessarily positive definite, and b,l,u are vectors in . It is clear that the image restoration problem (1.4) with nonnegative constraints is a special case of BCQP if we regard x as f, l as 0 and u as ∞. Before applying the PBB method to our problem raised from image restoration, we investigate the PBB method for general box-constrained quadratic programming (4.1).

Let us define the feasible set of (4.1) as In 4, the authors choose P_Ω as the projection operator on Ω in the following form (31) where mid(l,x,u) is the vector whose i-th component is the median of the set {l_i,x_i,u_i}. Ideally, the projection P_Ω should be chosen such that (32) And for our problems with l  = 0 and u = ∞, we choose the projection operator on Ω as (33) and the i-th component of P_Ω can be expressed simply as (34)

Assume that the current iterate x_k is feasible, then the next point can be obtained by where g_k:=g(x_k) = Ax_k − b is the gradient direction and α_k is the stepsize. In the PBB method, the choice of the stepsize is based on (1.11) and (1.12). We prefer using (1.11), where our reasons are given in Remark 1. We also find that the BB method is essentially a gradient method with the particular stepsize (1.14) and (1.15); and the PBB method projects the new point to the nonnegative quadrant.Remark 1 In practice, (1.11) is often superior to (1.12). This can be proved by inspecting the spectrum of A. If A is badly conditioned or A has some small eigenvalues, then the denominator of (1.12) will be smaller than the denominator of (1.11). Hence, the stepsize in (1.12) has large jumps. This shows that (1.11) is more feasible in applications.

To apply the PBB method to our problem, we rewrite the equation (1.4) as the equivalent standard quadratic programming form (35)

Noticing that the Hessian matrix is and the gradient is , the PBB method can be easily transplanted.

To safeguard the decrease of the sequence in each iteration, it is reasonable to add the line search strategy. The widely used line search method is the Armijo–Goldstein inexact line search strategy, that is, an acceptable step should satisfy the following conditions for some argument  β > 0 (32) (36) (37) where λ₁ ≤ λ₂ are two positive parameters in (0, 1). However, as is pointed out in 4, the nonmonotonic behavior of the BB method is lost, and the good performance of PBB method will be degraded. Considering these shortcomings, we adopt the adaptive nonmonotone line search method developed in 4 (a similar technique can be also found in 23): let be the current least value of the objective functional over all past iterates, i.e., at the k-th iteration, (38) Define a candidate function value to be the maximum value of the objective functional since the value of was found. Then find a reference function such that (39) In each iteration, the reference value should be improved. The method involves a preassigned small integer parameter L > 0, and is reduced if the method fails to improve on the previous least value of in at most L iterations. Therefore, this method does not require the sufficient reduction in , it is much more adaptive. Initially, we set . This choice of allows on early iterations. If the method can find a better functional value in finite iterations k_finite ≤ L, then the values remain unchanged. Otherwise, if the iterations exceed L, the value of and need to be reset, that is, , .

In our algorithm, to be sure that the first step is a decreasing step, we use the Armijo–Goldstein inexact line search strategy instead of the PBB step. And, we use the following stopping condition (also recommended in 4 and 13) in our numerical tests: (40) where  ϵ is a preassigned tolerance and is defined as Remark 2 For the iterative methods, the iterative index k also serves as the regularization parameter 25,31. Therefore, the iteration should be terminated in finite steps, otherwise noise will accumulate and the restorations will not be satisfactory. For our algorithm, the iterative index k is controlled by the parameter ϵ. In our numerical tests, we choose ϵ = 10^− 6 for 1D image restoration problem (small-scale problem) and ϵ = 10^− 5 for 2D image restoration problem (large-scale problem). We also note that there is no need to choose a smaller ϵ, since according to the inversion theory, a saturation state exists for iterations 31. At such a state, further iterations cannot improve the precision of the solutions. On the other hand, a larger  ϵ can yield faster convergence. However, insufficient iterations will decrease the precision of the approximations. Empirically, we suggest choosing  ϵ between 10^− 5 and 10^− 3.Now we can describe the PBB method for our image restoration problems as follows:Algorithm 1 (PBB method for image restoration)

Step 1 Given initial point , L  = 10 and set k:= 1;

Step 2 If (4.11) is satisfied, stop; otherwise, set ;

Step 3 If k  = 1, computing the stepsize α_k by Armijo–Goldstein inexact line search strategy; otherwise, computing α_k as (1.11);

Step 4 Set ;

Step 5 Safeguard the global convergence by the above mentioned adaptive nonmonotone line search technique, set k:=k + 1, go to Step 2.

5. Remarks on the convergence and regularizing properties

Let {x_k} be the sequence generated by the BB method from initial vectors x₀ and x₁. Then the gradient of the object function q(x) at x_k is g_k = Ax_k − b, and we have for all k  ≥ 1, (41)

To analyze the convergence of the BB method, we can assume without loss of generality that an orthogonal transformation is made that transforms A to a diagonal matrix of eigenvalues diag(λ_i). Moreover, if there are any eigenvalues of multiplicity m > 1, then we can choose the corresponding eigenvectors so that for at least m  − 1 corresponding indices of g_k. It follows from (1.9) and (5.1) and using that (42) Now many things can be deduced from the recurrence. Barzilai and Borwein prove an R-superlinear convergence result for the particular choice of the stepsize α_k. Also Raydan 17 has shown that the BB method with either stepsize formula is globally convergent in the strictly convex quadratic case.

Since all gradient methods satisfy , that is, the Krylov properties. Therefore, there are a number of reasons that might lead one to doubt whether the BB method could be effective in practice. Note the fact that the BB method is nonmonotonic, this behavior may be the preferable properties of the BB method. The nonmonotonicity of BB refers to the fact that the objective functional q(x_k) may increase on some iterations in contrast to the SD method. The success of the BB method is the minimization of a quadratic function, subject to simple bounds by an active set or projection type of method. If the number of active constraints changes, as is often the case, then it is usually not possible to continue to use the standard CG formula for the search direction and yet preserve the termination and optimality properties. To do this, it is necessary to restart using the SD direction when a new active set is obtained. Therefore, it is more attractive to use the BB method in some way in this situation. The success of the PBB method is that the BB method is efficient in the exploration of a face which indicates there is no need to make a decision as to whether to leave the current face or to explore it further. It is also important to consider how the PBB method compares with the PG methods that incorporate CG steps. Details are given in numerical tests.

It is worth noting that the global convergence of PBB method (Algorithm 1) can be realized. In fact, if is updated an infinite number of times, then global convergence occurs. Assume that the opposite occurs, that is, is unchanged for all k sufficiently large. In this case there exists an infinite subsequence of iterations k_i, such that k_finite is reached and is reset to . Note that because is a recent value of for which . Thus, the values of which are reset on iterations k_i are strictly monotonically decreasing. Hence, there exists a subsequence on which decreases without bounds, which contradicts the fact that is unchanged. This contradiction shows that the global convergence of Algorithm 1 can be ensured. Note that BCQP is a convex optimization problem, thus the global convergence of Algorithm 1 indicates the convergence of the iterates {f_k} of PBB.

For the ill-posed image restoration problem, the resulting kernel matrix is ill-conditioned. Therefore, like the SD method and CG method, the BB method becomes slow after successive iterations. At such a stage, further iterations may involve more round-off errors and noise. Therefore, the regularization technique is a must. As is summarized in section 2, there exist a large amount of methods for ensuring regularizing properties. We recall that the BB method is the specific gradient method. Nashed 16 had proved the regularization of the SD method for singular linear operator equations; the similar results hold for the BB method. It seems reasonable that PBB will share some of the regularizing properties of BB, but a rigorous proof of this is not an easy task.

It is well known that for iterative methods, regularization can be obtained by the truncation of iteration steps after sufficient iterations. As is noted in Remark 2, at a saturation state of iterations, further iterations cannot improve the precision of the solutions. Therefore, numerically we add another stopping rule, that is, we set a maximum iteration number k_max, if the iterative index k exceeds k_max, the iteration of Algorithm 1 should be stopped. It is worth noting that the choice of k_max is not empirical. Generally speaking, it should be a finite small integer, preassigned by users.

6. Matrix-vector multiplication

We suppose that the PSF kernel function in (2) is spatially invariant, that is, the kernel is separable and can be reformulated as (43) This indicates that the blurring is identical in all parts of the image and separates into pure horizontal and pure vertical components.

Numerically, assume that the discretization of k_x and k_y are and respectively, then the matrix is a tensor of and , i.e., the Kronecker product of and , (44) ‘’' notation is a useful tool in simplifying the expression of the matrix-vector multiplication. Given an array , one can obtain a vector by stacking the columns of U. This defines a linear mapping , Therefore the equation (1.4) can be rewritten as (45)

6.1. MVM: FFT-based method

It is obvious that the main cost of computation in our PBB algorithm for image restoration is the matrix-vector multiplication (MVM), so it is necessary to give an efficient algorithm to compute the MVM. Generally speaking, a classical MVM accounts for the 2m² flops if we regard the length of the signal f as m.

Note that both and are matrices of the Toeplitz type. Therefore, their Kronecker product in (3) is a block Toeplitz with Toeplitz blocks (BTTB). By extending the BTTB into a block circulant with circulant blocks matrix (BCCB), we can use the 2D discrete Fourier transform to compute the MVM 15,25.

The BCCB matrix can be decomposed as where is the 2D discrete Fourier transform matrix, and Λ is a diagonal matrix containing the eigenvalues of . The eigenvalues of can be obtained by computing a 2D discrete Fourier transform (DFT) of the first column of , so we can compute by .

DFTs can be computed at a low computational cost by utilizing the fast Fourier transform (FFT). The Fourier transform of an m-vector (signal) can be computed in operations.

6.2. MVM with sparse matrix: a heuristic approach

In atmospheric image restoration, the PSF is often modeled by a Gaussian function. Actually, the Gaussian function closely simulates the convolution process of the true signal with the PSF operator. Both the blurring by aerosols and turbulence can be taken as a Gaussian, which are in the form (46) where  σ is a positive constant. The larger we choose σ, the more f gets smoothed. So by the same argument, the smaller we choose σ, the more the convolution result resembles f.

In our numerical experiments, we use the Gaussian PSF as the integral kernel k in (1.2), so can be represented by a kronecker product of two low order matrices as with , . For the blurring process if A and B are taken to be sparse-banded matrices 10, only pixels within a distance band–1 contribute to the blurring. So, we can use a very economic algorithm proposed by 29,30. Let us take band–2 and band–3 as examples. Similar discussions can be made for other bands of matrices. Practically, the bandwidth is usually taken as 3.

Suppose , then A, B are tridiagonal matrices. Pixels within a distance 1 of A and B contribute to the blurring. The different elements of are only C = A(1:2,1)⊗B(1:2,1). The resulting matrix is a sparse BTTB with each block a tridiagonal matrix. If we define then C:=(C₁,C₂,C₃,C₄)^T = (a₀b₀,a₀b₁,a₁b₀,a₁b₁)^T. Thus, we can write the MVM as follows: where Then so we can give the MVM algorithm in a Matlab code as follows:Algorithm 2 (Banded BTTB MVM)

function y = MatVecTri(m,n,C,x)

y = blockmulti(m,n,C(1:2),x);

x = blockmulti(m,n,C(3:4),x);

y(1:n*(m-1))=y(1:n*(m-1))+x(n + 1:m*n);

y(n + 1:m*n)=y(n + 1:m*n)+x(1:n*(m-1));

function b = blockmulti(m,n,D,x)

b = zeros(m*n,1);

tmp = D(2)*x;

b(1:m*n-1)=tmp(2:m*n);

b(n:n:m*n)=0;

b = D(1)*x + b;

tmp(2:m*n)=tmp(1:m*n-1);

tmp(1:n:m*n)=0;

b = b+tmp;In Algorithm 2, y  = MatVecTri(m, n, C, x) is a main function, which calls the block multiplication function b = blockmulti(m, n, D, x) to finish the BTTB MVM.

Suppose , then A, B are five diagonal matrices. Pixels within a distance 2 of A and B contribute to the blurring. The different elements of are only C = A(1:3,1)⊗B(1:3,1). The resulting matrix is a sparse BTTB with each block a five diagonal matrix. Similar algorithms can be made as is in Algorithm 2.

The cost of Algorithm 2 is only 4mn multiplications. For the five diagonal matrices, the cost of the MVM computation would be 9mn. Whereas for FFT based matrix-vector computation, the cost is , which is greater than 4mn and 5mn for banded MVM for large m and n, say, m = n = 256, 512 or more.

7. Numerical experiments

7.1. 1D Image restoration problem

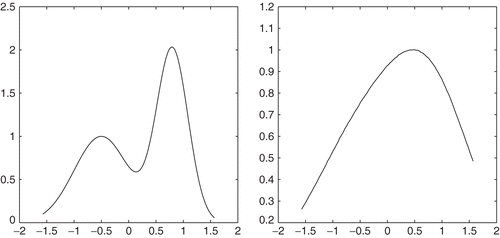
First, we consider an 1D image restoration problem. Practical image restoration problems are in 2D space. The forward model is an 1D Gaussian PSF convolution equation (47) where ,  σ is a positive constant. The input signal f is a simple function with two ‘humps’ (48)

Taking , and  σ = 0.7, the right-hand vector h is obtained by multiplication of the (m × n)-dimensional matrix , approximating the operator in (7.1), by the column vector f of values of the exact solution on the grid in the interval (49) In order to simulate measurement inaccuracies, we add noise to the right-hand side h as follows where is random perturbation to the right-hand side with the same length as in h and is the noise level.

In this experiment, the performance of the BB, PBB, PLW, PG and GPCG methods are compared. We do not list the results for all the noise levels. Instead, we only compare the performance of these algorithms for a medium error level . To fully understand the iteration process for the methods BB, PBB, PLW and PG, we do not preassign a maximum iteration number. To make a fair comparison, we use the same stopping rule as in Algorithm 1, while different values of  ϵ are used for different algorithms, which lead to the regularization as is mentioned in Remark 2. For the GPCG, we adopt the algorithm described in 13. The stopping rule for CG is the same as in Algorithm 1. But we find that it is difficult to make a best balance between the GP iterations for the original problem and CG iterations for the reduced problem. In our experiments, we choose maximum iteration values for GP and GPCG, respectively, as 15 and 30, while for CG, the maximum iteration value is chosen as 30. In 13, it requires a large maximum CG iteration number, which is usually assigned to be 2*n. We remark that for ill-posed image restoration problem, the CG iterations cannot be large; otherwise, divergence will occur. The grids number to discretize the system is 100. This yields a matrix with size 100 × 100. 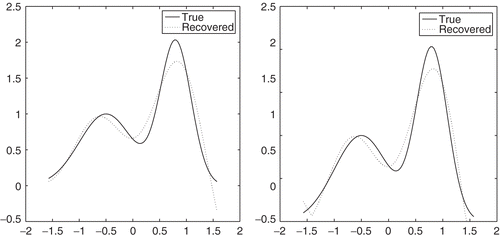The condition number of is 3.5985 × 10¹⁹, hence the discrete problem is highly ill-conditioned. The true image, blurred and noise image, and the restorations are respectively plotted in figures 1–4.

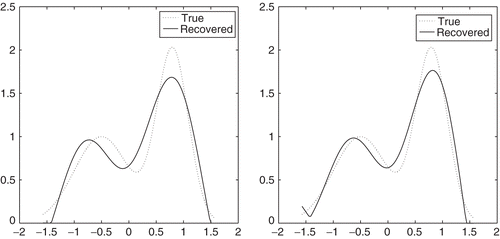
We denote the relative error between the true image and the restoration by rerr and record both the CPU time (seconds) and the total iteration numbers, as are shown in table 1. In this table,  ϵ is not assigned the same. For PLW, if ϵ < 5.0e − 5, nonconvergence will occur; for PG, BB, PBB and GPCG, the chosen values of  ϵ in table 1 are not optimal, but this choice can generate comparable results. It seems that PBB method outperforms other methods. As is known, both the PG and PLW methods inherit the slow convergence property of the SD and the Landweber iteration methods. So, it is not surprising that this behavior appears in table 1. Figure 4 (right) gives us a vivid illustration about the relative errors of every algorithm. It indicates that GPCG is a little better in practice and is comparable with PBB. But how to arrange in pairs about the PG step and CG step for highly ill-posed problems is not an easy task. Overall, due to the fact that the problem is small in scale, the performance is not so clear.

Figure 1. Left: true image; Right: blurred noisy image.

Figure 2. Restored images by BB method (left) and PBB method (right) ().

Figure 3. Restored images by PLW method (left) and PG method (right) ().

Figure 4. Restored images by GPCG method (left) () and relative errors for different number of iterations for all algorithms (right).

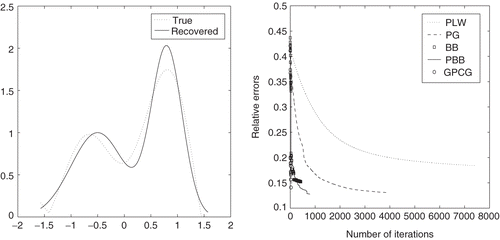
Table 1. The iteration results for error level

Methods	CPU time (secs)	Number of iterations	Relative error (rerr)	ϵ
PLW	11.897000	7470	0.18380	5.0e  − 5
PG	2.764000	3941	0.13051	1.0e  − 5
BB	0.121000	427	0.15214	1.0e  − 6
PBB	0.521000	796	0.12765	1.0e  − 6
GPCG	1.813000	30	0.14070	0.5

7.2. Atmospheric image restoration

In this section, we give examples on the restoration of atmospheric images. The blurring process is modeled by a Gaussian PSF: (50) In our test, we choose . And the noise n is assumed to be additive, which can be expressed as where N is the size of the image, randn(N²,1) is the Gaussian normal distributed random vector, and we set randn(‘state’, 0) in our Matlab codes to ensure the same random vector is generated every time. In our computation, the noise level  δ is generated as , where level∈(0,1).

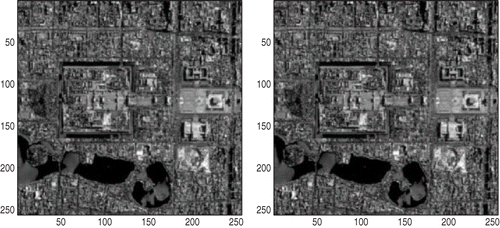
The image for testing is a calibrated remotely sensed image in Beijing with a size equalling to 256 × 256. The resulting PSF matrix is a BTTB with size equalling to and a bandwidth equalling to 5, that is, only pixels within a distance 3 contribute to the blurring.

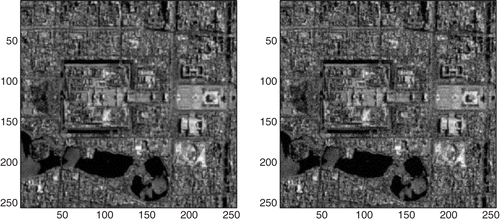
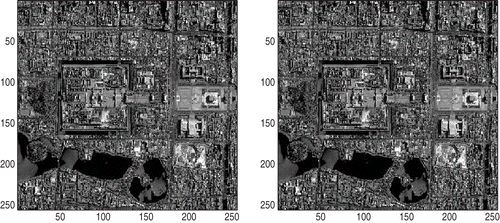
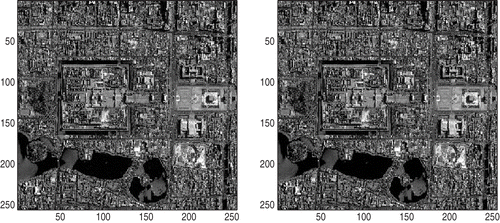
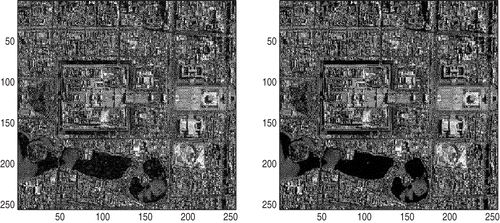
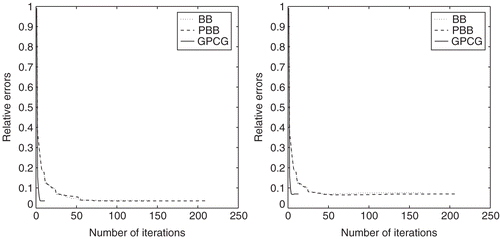
It is clear that the BB method can also be applied to our problems. Therefore, our numerical experiments consist of two parts. In the first part, we apply the BB method without any projection, and in the second part, the PBB method is performed. The true image is presented in figure 5.. And the blurred images with different noise levels: 0.005, 0.01, 0.05, 0.1 are presented in figures 6 and 7. Generally speaking, the noise level equalling to 0.1 is large enough; otherwise, we consider the observations/measurements to be unbelievable. The restored images are presented in figures 8–11.

Again, we denote the relative error between the true image and the restoration by rerr (as is in section 7.1) and set the maximum iteration number as k_max = 400. Note that the choice of the maximum iteration number k_max is not empirical. The reason we choose a maximum iteration number is because we do not consider further iterations to be necessary after reaching such a number k_max. However, such a regulation is never activated. Our algorithm converges before reaching the maximum iteration number.

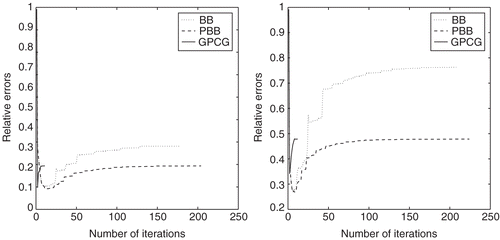
It has been shown that GPCG method is a well-developed method for solving large-scale bound-constrained quadratic programming problems. It has better numerical performance than other methods of gradient types 13 such as the SD method and the CG method 12 (as is illustrated in 1D example). Therefore, we only make a comparison of the GPCG method with the BB and PBB methods. The maximal iteration numbers for GPCG, GP and CG are assigned, respectively, as 20, 10 and 50. The iteration results by BB, PBB methods and GPCG method for different noise levels are listed in table 2. Figures 12 and 13 give us a vivid illustration about the relative errors of the three algorithms. It indicates that the performance of PBB is better than the others.

Figure 5. True image.

Figure 6. The blurred images for different noise levels: Left: level = 0.005; Right: level = 0.01.

Figure 7. The blurred images for different noise levels: Left: level = 0.05; Right: level = 0.1.

Figure 8. Restored images by BB method (left) and PBB method (right) (level = 0.005).

Figure 9. Restored images by BB method (left) and PBB method (right) (level = 0.01).

Figure 10. Restored images by BB method (left) and PBB method (right) (level = 0.05).

Figure 11. Restored images by BB method (left) and PBB method (right) (level = 0.1).

7.3. Discussions on the results

For the GPCG method, it is required to find the active constraints in every iteration step. Moreover, it is required to solve a successive quadratic subproblems by the CG method. For the BB and PBB method, the iteration is quite simple where only the gradient steps need to be computed. Note that the main computational cost of the image restoration problem is the MVM. So the method which costs less MVM operations is the preferred method.

As indicated from table 2, both the BB and the PBB method generate competitive results compared with the GPCG method. For the GPCG method, we can see that it costs much more MVM operations than the BB or the PBB method to get similar precision. Because the cost of MVM operation is expensive, GPCG, though requiring relatively fewer iteration steps, will be much slower than the BB or PBB method.

Table 2. The iteration results for different noise levels.

Methods	Iteration steps	Number of MVM	Relative error (rerr)	Noise level (level)
BB	140	290	0.0380	0.005
PBB	209	637	0.0358	0.005
GPCG	11	838	0.0358	0.005
BB	168	346	0.0761	0.01
PBB	209	637	0.0700	0.01
GPCG	13	1244	0.0701	0.01
BB	178	366	0.3814	0.05
PBB	204	622	0.2937	0.05
GPCG	11	1092	0.2938	0.05
BB	210	430	0.7629	0.1
PBB	224	682	0.4783	0.1
GPCG	12	1262	0.4783	0.1

Figure 12. Relative errors for different number of iterations for all algorithms (Left: level = 0.005; Right: level = 0.01).

Figure 13. Relative errors for different number of iterations for all algorithms (Left: level = 0.05; Right: level = 0.1).

8. Conclusion and future works

In this study, we applied the BB method and PBB method to nonnegative image restoration problems. The numerical results show that these methods are promising for large-scale image restoration problems.

Though the PBB method can obtain a closer approximation of the true image, the iteration is a little larger. So, the selection of the line search strategy and adopting some kind of preconditioning to accelerate the convergence rate deserve further research. Besides, the PBB method for ill-posed inverse problems, not limited to image restoration problems, seem to be a regularization. But a rigorous proof deserves further studying.

Acknowledgements

We would like to express our sincere thanks to the anonymous referees' valuable suggestions which greatly helped us improve the quality of the article. We also wish to express our particular thanks to Mr. Jack Teng for his careful reading and polishing the article which led to the current more readable version of the article. The research is sponsored by China National Natural Science Foundation 10501051.