An inversion method for identification of elastoplastic properties for engineering materials from limited spherical indentation measurements

Abstract

In this article, a new method for determination of elastoplastic properties from an indentation loading curve is proposed. Mathematical model, based on deformation theory, leads to quasi-static elastoplastic contact problem, given by the monotonically increasing values α_i>0 of the indentation depth. The identification problem is formulated as an inverse problem of determining the stress–strain curve from an experimentally given indentation curve . The inversion method is based on the parameterization of the stress–strain curve, according to the discrete values of the indentation depth, and uses only a priori information as monotonicity of the unknown function . It is shown that the ill-conditionedness of the identification problems depends on the state discretization parameter Δe_i. An algorithm of optimal selection of state discretization parameters is proposed as a new regularization scheme. Numerical examples with noise free and noisy data illustrate applicability and high accuracy of the proposed method.

Keywords:

• Determination of elastoplastic properties;
• Spherical indentation;
• Inversion method;
• Ill-conditionedness;
• Regularization

Keywords:

• AMS(MOS) subject classifications:
• 35R30
• 73C50
• 35J85

1. Introduction

Spherical indentation testing is one of extensively used experimental methods to measure the hardness of metal and polymer materials. The objective is usually to analyze the indentation curve as dependent on the size of the sample (indent) and indenter relative to the material length parameters, strain hardening, and yield stress to modulus ratio. The idea of relating the mechanical properties of deformable materials to their hardness was first given in 10. By using the method of characteristics for hyperbolic equations, he has found a relationship between the Brinell hardness , and the yield stress: , for a spherically symmetric indentation hardness test (here and below P > 0 is the measured loading force, R > 0 is the radius of a spherical indenter and α > 0 is the indentation depth). However, in this model curvature of a contactable surface was ignored, and the problem was considered for a perfectly plastic material. Subsequently, the relationship between hardness as measured data and stress–strain behavior in the regime of “large” indents have been established in 12, 13, 21. Later technological advances and the need to find experimentally unmeasurable material properties by using measurable one on a small scale, led to an increasing interest in the development of new methods. Most of these methods may be divided into two groups. The first group contains various plasticity theories and models that can adequately describe spherical indentation testing. Reformulating gradient plasticity theory Fleck and Hutchinson 4 proposed generalization of the classical J₂ flow and deformation theories. Solutions of basic problems show that, when stressing is nearly proportional, as the case of spherical indentation is, the new plasticity models predict qualitatively similar behavior to the J₂ flow and deformation theories. Wei and Hutchinson 23 demonstrated recent trends in micron scale indentation and comparative analysis of existing plasticity models. Comparing all the plasticity models used for the spherical indentation, Budiansky 2 and Fleck and Hutchinson 4 concluded that the deformation theory version of J₂ theory is used rather than the flow theory version not only because it is easier to implement numerically, but also because it gives essentially identical predictions to the flow theory, when stressing is nearly proportional (simple loading). In the second group, various analytical and numerical methods have been developed to extract elastoplastic properties of deformable materials from a measured spherical indentation loading curve (see 17, 20 and references therein). A study to extract the plastic properties of power hardening engineering materials from spherical indentation loading curve have also been given in 3. The results obtained here show that the identification/inverse problems related to determination of the elastoplastic properties of materials based on indentation tests, have ill-conditioned nature. For near linear hardening materials, numerical relationships between material properties and indentation responses have been obtained in 18–19. A utilization of connection between the indentation curve and other mechanical properties, in particular Brinell Hardness, were given in 1,16.

Within the framework of the J₂-deformation theory of plasticity, the mathematical theory of inverse problems related to determination of elastoplastic properties from an indentation loading curve has been formulated by the author 5–6. The analysis given in 6 and based on the parametrization of the stress–strain curve, shows how the inverse problem becomes an ill-conditioned one, by increasing the value α > 0 of the indentation depth. Taking into account this analysis, a new regularization algorithm – an optimal selection of the indentation parameters _i>0 – was proposed. This algorithm also allows to solve an inverse problem of determining the relationship σ_i=σ(e_i), by using a limited number of measured data , 7.

In this article, an inversion method to extract the elastoplastic properties of engineering materials from the measured spherical indentation (loading) curve is proposed. In order to make the proposed method applicable to wide material behaviors, with respect to the hardening properties of the material it is only assumed that the relationship σ_i=σ(e_i) is a monotone increasing and concave curve. Such a model includes wide hardening relations, in particular power hardening, linear and piecewise linear hardening ones. Section 2 involves the mathematical model of an axisymmetric spherical indentation and analysis of the relationship σ_i=σ(e_i). Then within the framework of this model, formulation of the inverse problem of determining the stress–strain curve σ_i=σ(e_i) from the measured indentation curve is defined. Section 3 contains an ill-conditionedness analysis of the inverse problem. Linearization of the forward problem and convergence of solution are given in section 4. Computational framework of the forward problem with the remeshing algorithm are presented in section 5. In section 6, a parametrization of the inverse problem and the inversion algorithm are discussed. An example related to the ill-conditionedness of the inverse problem and an algorithm of optimal selection of the state discretization parameters and relaxation of monotonicity condition for slopes, are also given in this section. Section 7 contains computational results for different engineering materials with exact and noisy data to show applicability and accuracy of the presented inversion method. The final section 8 summarizes the main contributions made by the presented methodology. Presented numerical results show that the inversion method given in this article allows to determine with high accuracy the parameterized curve σ_i=σ(e_i) from the spherical indentation loading curve for different engineering materials.

2. The mathematical model

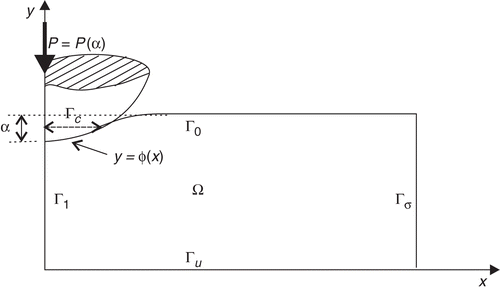
Let the rigid spherical indenter be loaded with a normal loading force , into an axially symmetric homogeneous body (sample) occupying the domain Ω×[0, 2π], in the negative y-axis direction, as shown in figure 1. The uniaxial quasi-static indentation process is simulated by monotonically increasing the value α > 0 of the indentation depth. It is assumed that the indentation process is carried out without unloading, moment, and friction. For a given value α∈(0, α*) of the indentation depth, the quasi-static axisymmetric indentation process can be modeled by the following contact problem.

Figure 1. Geometry of the spherical indentation.

Find the displacement field u(x, y)=(u₁(x, y), u₂(x, y)) from the solution of the unilateral problem (1) (2) (3) (4) (5) Here , l_x, l_y >0, , , , and is the surface of the spherical indenter, with the radius r₀.

The relationship between the components of strain and stress tensors is as follows: (6) where the components of deformation, and (7) λ, μ >0 are Lame constants, E > 0 is an elasticity modulus, ν is the Poisson coefficient and G=μ is the modulus of rigidity.

The system of Lame equations (1) represents an equilibrium equations for an axially symmetric body, in the cylindrical coordinates (r, z):=(x, y), within the range of J₂-deformation theory of plasticity, where strain and displacements are assumed to be small. As shown in experimental and theoretical studies (see 2, 4, 22 and references therein), the deformation theory provides a highly accurate approximation to the flow theory solution, when proportional or nearly proportional stressing occurs throughout the deformable body. Hence in the case of simple loading, i.e., proportional stressing, which holds for the spherical indentation without moment, J₂-deformation theory of plasticity is used due to its simplicity in numerical simulations. Furthermore, in conventional physical model of spherical indentation 4, 17, 18, 22, the friction between the indenter and the indented material has a negligible effect on the indentation curve and for this reason the contact on the common surface between the indenter and the sample can be assumed frictionless. Since an indentation test is nondestructive one (shallow indentation) and can be applied both to small samples or to fabricated machine and structural elements, the above physical model is used for large class of pure and alloyed engineering materials 2–4, 17, 19, 20.

It is assumed that an axisymmetric sample lies on a substrate without friction, as conditions (5) show. Furthermore, the symmetry of the sample implies the boundary conditions (4). On the part of the boundary Γ_σ, beyond on the contact, the “free boundary conditions” (3) are given. The contact conditions (2), in the form of inequality, means that the contact zone , depending on the value α > 0 of the indentation depth, is also unknown and need to be defined.

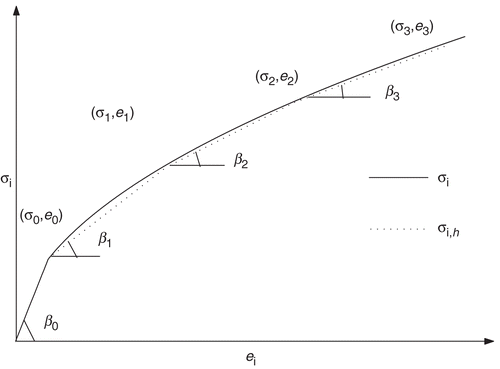
According to the J₂-deformation theory, the stress–strain relationship is assumed to be in the following form (figure 2): (8) where , is the strain intensity. The function is assumed to be a monotone increasing concave one. The plasticity function g=g(ξ), is assumed to be piecewise differentiable and satisfies the following conditions 14: (9) The case g(ξ)=0, ξ∈[0, ξ₀] and corresponds to pure elastic deformations.

Figure 2. Stress–strain curve and its parameterization.

The stress–strain relationship (8), which describes the elastoplastic behavior of a wide range of engineering materials, has been used in our analysis. Note that the power law description (10) is also widely used to approximate the plastic behavior of metal materials 3,18, 23, corresponds to the power hardening materials for which the stress–strain relation is given by the Ramberg–Osgood curve Here κ∈[0,1] is a strain hardening exponent. The cases g(ξ)=0 and in (8) correspond to pure elastic (κ = 1) and perfectly plastic (κ = 0) materials, respectively.

The inverse problem consists of identifying the stress–strain curve , given by (8), from the measured spherical indentation loading curve , α∈(0, α_K), during the quasi-static indentation process. Accordingly, the unilateral boundary value problems (1–5) is defined to be a forward problem.

Note that indeed the indentation curve consists of loading and unloading parts. In the considered model, we use only the loading of the part indentation curve, since the Ramberg–Osgood type of materials are considered. This, in particular, means that the residual penetration depth α∈(0, α_K) and loading force should be used as a given data in the considered inverse problem. The unloading solution can be generated numerically from the solution corresponding to pure elastic case (for details of such indentation morphology, see 16, 17).

In the considered model, the Poisson coefficient ν∈(0, 0.5) is assumed to be known and has been taken ν = 0.3. Hence, in the case of pure elastic deformations ((e_i≤e₀)) one needs to determine the elasticity limit e₀ > 0, and in the case of plastic deformations (e_i≥e₀) the plasticity function g=g(ξ) needs to be identified. The elasticity limit e₀ > 0 will be determined by a special algorithm. Here and further it is assumed that the indentation interval (0, α₀), α₀ <α_K corresponds to pure elastic deformations.

3. Analysis of the inverse problem

The identification/inverse problem of determining the hardening behavior from the measured spherical indentation loading curve is a complicated nonlinear process, which deals with elastoplastic material behavior. Evidently, no analytical solution for indentation response is available. In addition to all difficulties, the inverse problem arising here is an ill-conditioned one. To demonstrate this main distinguished feature, let us reformulate the inverse problem as the following nonlinear operator equation (11) Here Σ ={σ_i(e_i)} is the set of monotone increasing concave functions (stress–strain curves), defined on (0, e_M), and is the set of monotone increasing convex functions (indentation loading curves), defined on (0, α_K). To find out the structure of operator , one needs to take into account that for each value α∈(0, α_K) of the indentation depth, the theoretical value P_α:=P_α(σ_i) of the indentation loading force is defined as follows: (12) where the function u=u[σ_i] under the integral is the solution of the contact problem (1–5), corresponding to the unknown function σ_i=σ_i(e_i), i.e. the unknown parameters E, e₀ and g(ξ). Comparing the right hand side of (12) with (11), one can see that for each α > 0 the operator represents an integral operator. Thus for each step of the quasi-static indentation, the inverse problem can be reformulated as the following nonlinear integral equation: (13) It is well known that the integral operator given by (12) is a continuous compact operator in the class L₂ of square integrable functions. On the other hand, due to Tikhonov's lemma 22, the class of monotone increasing and uniformly bounded functions is compact in the class L₂. Thus the inverse problem (11) has a unique solution in the class Σ, for each noise free data . 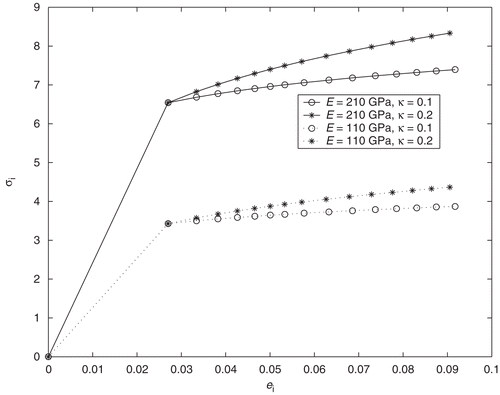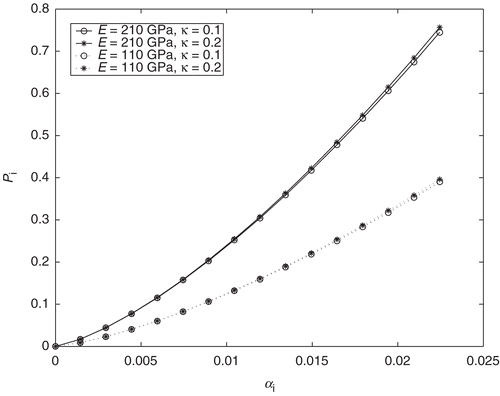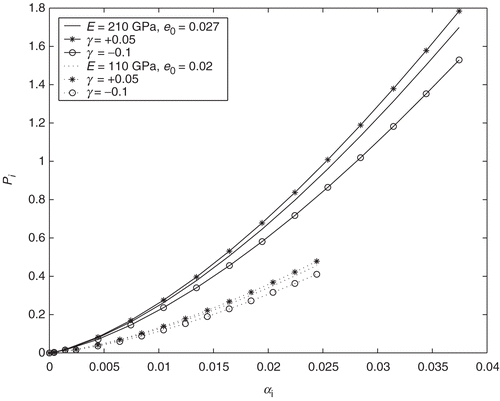However, this problem is not well conditioned in the sense of Hadamard, due to sensitivity of the solution with respect to the measured data , as shown in 6. To show the nature of this ill-conditionedness in the case of power hardening materials, the following computational experiment has been realized for two types (rigid and soft) of materials (E₁=210 GPa; E₂=110 GPa) with different power hardening parameters (κ₁=0.1; κ₂=0.2). The stress–strain curves, given by (10), of these materials are plotted in figure 3 (in all cases e₀=0.027). The corresponding theoretical values of the indentation loading curves P=P(α), α∈(0, α_K), has been obtained from the numerical solution of contact problems (1–5). The results, plotted in figure 4, show that the inverse problem is most sensitive when the tested materials obey the same linear hardening behavior, but different hardening parameters. Thus, for the first type of materials (with E₁=210 GPa, and κ₁ =0.1, κ₂ =0.2) the maximum relative difference in the value of the loading force is P(α); E₁, κ₁)| is , while maximum relative difference in the stress–strain curves is . The same results have been obtained for the second type of materials (with E₂=110 GPa, κ₁ =0.1 and ): , while .

Figure 3. Stress–strain curves for different engineering materials.

Figure 4. The indentation curves corresponding to the data in figure 3.

These results show that the indentation curves corresponding to different power hardening materials, with the same modulus of elasticity E and different power hardening parameters κ₁≠κ₂, may not be distinguishable. For these materials, the inverse problem (11) is most sensitive: small perturbations in the right hand side leads to essential deviations in the values of the function σ_i=σ_i(e_i).

The above analysis can also be obtained from equation (13), rewriting it for pure elastic and plastic deformations, separately. Indeed, due to homogeneity of equation (1) and the Neumann boundary conditions (2–5) with respect to the elasticity modulus E > 0, by using (6) and (7) in (13), and taking into account g(ξ)=0, we get (14) This formula shows that the unknown elasticity modulus E > 0 can be found explicitly by solving the contact problems (1–5) for E = 1. Here (15) and u=u(x, y) is the solution of the contact problems (1–5) for E = 1. Hence for pure elastic deformations the inverse problem (13) is well conditioned, and the elasticity modulus can be determined explicitly. In the case of plastic deformations (e_i> e₀) the inverse problem with respect to the plasticity function g=g(ξ) can be formulated as the following nonlinear boundary integral equation (16) where the function u=u[E, g] under the integral is the solution of problems (1–5), corresponding to E and g=g(ξ).

The operator/integral equation forms (11), (14), and (13) of the inverse problem are convenient only for its analysis, but not for subsequent numerical solution, since due to measurement errors in the given data exact fulfillment of these equations is not possible. We introduce the auxiliary functional (17) and define a quasisolution 11, 22 of the inverse problem, according to 4 as follows: (18) An existence of a quasisolution is proved in 5.

4. Analysis of the forward problem: linearization and convergence

Multiplying the first equation by u₁(x, y) and the second one by u₂(x, y), and applying the Green formula, we define the weak u∈V solution of the nonlinear unilateral problems (1–5) as a solution u∈V of the following variational inequality (19) Here (20) is the nonlinear form and is the closed convex set of admissible displacements, is the subspace of the Sobolev space H¹(Ω) of vector functions u(x, y) 15. We take into account the axially symmetricity of the problem and define the H¹-norm as follows: As it follows from the general theory of variational inequalities for monotone potential operators 6, 15, the variational inequality (19) has a unique solution u∈V, if conditions (9) hold.

We will denote the nonlinear functional (20) by a(u;u,v):=(Au, v) to show the dependence of the nonlinear terms on the function u=u(x, y). For e_i(u)≤e₀ the nonlinear functional a(u;u,v) becomes the bilinear one, and we will denote it by (21) As it was noted above, the variational problem (19) is nonlinear not only due to the presence of the plasticity function , but also, in the sense that for each value α > 0 of the penetration depth, the contact zone is unknown, and needs to be also determined. For this reason, we will organize here two iteration procedures in order to linearize the nonlinear forward problem: first, with respect to the unknown contact zone, and the second one, with respect to the plasticity function .

Let us assume that the unknown contact zone Γ_c(α) is found by any way. Then the unilateral boundary conditions (2) will be separated into following the mixed boundary conditions: (22) (23) In this case, the unilateral problems (1–5) will be transformed to the mixed boundary value problems (1), (3–5), (22–23), which in subsequent will be defined as the problem (P_c). The solution of this problem will be denoted by u(x,y):=u[x, y; Γ_c].

Let now be a given perturbed contact domain: . Then, either (i.e., ), or (i.e., ). Since is assumed to be given, the unilateral boundary conditions (2) will be seperated into the following mixed boundary conditions: (24) (25) The unique solution of the mixed boundary value problems (1), (3–5), (24–25) (in subsequent, the problem ), corresponding to the perturbed contact zone , will be denoted by . Note that depending on or the inequalities (2) change signs, accordingly. This result, obtained in 8, will be used below, in the remeshing algorithm.

In pure elastic case (g(ξ)=0), the following result shows a relationship between the solutions u=u(x, y) and of the problems (P_c) and .

LEMMA 1 

Let v₁(x, y) = 0, x∈Γ₁} be solutions of the mixed problems (P_c) and , corresponding to true Γ_c⊂Γ₀ and perturbed contact domains, respectively. Assume that g(ξ)=0, and . Then the following assertions hold:

(a) if then (26)

(b) if then (27)

Proof 

Let us first assume that and . Evidently the solutions ⟨u(x, y);Γ_c⟩ and of problems (P₁) and satisfy the following integral identities, respectively Assuming that , from these integral identities we obtain According to the boundary conditions (22) and (24) . This implies (26).

The second integral identity (27) can be obtained by the same way. ▪

By using the coercivity of the bilinear form a(u, v) on the left hand side and applying the Cauchy inequality with the mean value theorem on the right hand side of (26) and (27), we have the following

COROLLARY 1 

Let conditions of Lemma 1 hold and σ₂₂(u)∈H⁰(Γ₀). Then the following estimates hold:

(a) if then where

(b) if then where

This result suggests an idea of approximation of the variational inequality (19) by the corresponding integral identities of types (26) and (27).

THEOREM 1 

Let g(ξ)=0 and σ₂₂(u)∈H⁰(Γ₀). Assume that , , meas , ∀m, be a sequence of a priori given contact domains. Denote by , the sequence of corresponding solutions of problems : If the sequence converges to Γ_c, in the sense that , as m→∞, then the sequence of solutions converges to the solution of the problem (P_c), in the norm of the space H¹(Ω).

Proof 

Due to Corollary 1, the difference of solutions u(x,y):=u[x, y; Γ_c] and can be estimated as follows: (28) (29) depending on or , accordingly. Here As , the right hand sides of inequalities (28) and (29) tend to zero, which means , as m→∞. This implies the proof. ▪

Consider now the case g(ξ)>0. Taking into account the nonlinear term g=g(e_i(u)) in (20), we rewrite it as follows (30) Then we linearize the nonlinear problem (P_c) by Kachanov's method 14: (31) We define this mixed problem as the problem (P_n). Taking into account (30), the potential of this problem can be defined as follows 9: where are the coefficients from n − 1-th iteration (see (7)). If conditions (9) hold, then the rate of convergence of the sequence of solutions of problems (P_n), to the solution of the problem (P_c) can be estimated via the monotone decreasing convergent sequence of potentials {Π₀(u⁽ⁿ⁾)} as follows (see, Theorem 2 9): (32) Let us now substitute in (31) and denote it by , the solution of the obtained problem [the problem . Then combining Theorem 1 and estimate (32) we have the following convergence

THEOREM 2 

Let conditions of Theorem 1 hold and the plasticity function g=g(ξ) satisfies conditions (9). Then the sequence of solutions of problems converges to the solution of the problem (P_c) in H¹-norm, as m, n→∞.

Proof 

If u=u[x, y;Γ_c] is the solution of the nonlinear problem (P_c), the difference can be estimated as follows: Here u_n=u_n[x, y;Γ_c] is the solution of the linearized problem (31) [the problem (P_n)]. The first norm on the right hand side tends to zero as n→∞, due to (32). The second norm also tends to zero as m→∞, according to Theorem 1. Hence , as m, n→∞, and we obtain the proof. ▪

5. The remeshing algorithm for the forward problem

Since an accuracy of the numerical solution of the inverse problem highly depends on the accuracy of the corresponding forward problem solution, one needs to solve the forward problem effectively on an acceptable finite-element mesh. As was noted above, the main difficulty in solving the forward problem is the determination of the unknown contact zone Γ_c(α), on each step of indentation.

The above linearizations permit one to construct an iteration procedure for the considered indentation problem. Consider the sequence , , of perturbed contact zones. Then for a given one needs to solve the linearized forward problem .

For each α∈(0, α_K), the iteration scheme for the forward problem (P_c) is as follows:

i.	For a given α01 < α0 (pure elastic case: g(ei)=0), choose an initial iteration for the contact zone, solve the problem and find the value . If , then choose the next iteration , with ; if , then , H_c > 0.
ii.	Repeat the step (I) for m + 1 until the fulfillment of the condition (33) where ϵσ>0 is a given accuracy.
iii.	For a given α1 = α0+ Δα (g(ei)≠0), choose an initial iteration , and solve the problem for n=1, 2, 3, …, until the fulfillment of the condition (34) where ϵu>0 is a given accuracy.
iv.	Use the approximate solution and choose the next iteration according to the step (I). Use this iteration in (III) and find the next iteration . Repeat this process for the iteration , until the fulfillment of the conditions (19) and (20).
v.	Continue the steps (III)–(IV) for the next values αp = αp−1+ Δα, p=2,3, …,K.

Finite-element discretization of the linearized forward problems is performed by using linear Lagrange type of triangle elements. Due to the linearity of the interpolant u_I(x, y) of the function u(x, y), the deformation intensity will be a constant for each finite element. For a given value α_k>0 of the indentation depth, the maximal value of the deformation intensity for all finite elements Δ_h⊂Ω will be denoted by , where the index p=1, 2, 3,… denotes the number of deformation states, corresponding to the parameter α_p. Evidently, for α =α₀ the value e₀=max_Δhe_i(u) is an elasticity limit.

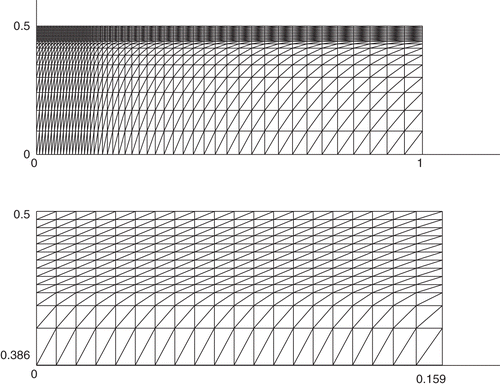
The first part of the computational experiments was related to the optimization of the finite-element mesh used for the quasi-static indentation problem, since a piecewise uniform finite-element scheme may not converge at all if the fine mesh step is not sufficiently small in relation to the coarse mesh step. For this reason, the mesh convergence study was first performed in order to determine an adequate number of nodes and elements in the sample Ω =[0,1]× [0, 0.5] cm. This is done by running different discrete models with increasing number of finite elements until the difference between contact pressure corresponding to two consecutive mesh models becomes negligible. Finally, the piecewise uniform optimal mesh with the parameters N_x = 50, N_y = 20 (the number of mesh points on the intervals [0, l_x] and [0, l_y], respectively), shown in upper figure 5, is constructed. The uniform fine mesh with the mesh steps , defined in the strip (lower figure 5), contains the admissible contact zone, and is localized in a small area under the indenter, where, as expected, the maximum stress magnitudes arise. Here is the mesh point corresponding to the boundary of the contact zone. The uniform fine part was continued to the right along the boundary Γ₀ for two mesh points , k = 1, 2, so that the boundary of the contact domain always remains in the fine mesh: . In all remeshing process, the number of mesh points of the fine mesh remains constant. Outside of the strip Ω₁ the coarse mesh, with slowly increasing mesh steps is defined. Here N_p is the number of mesh points in the interval (a_c, l_x), correspondingly. However, once the contact zone for a given value of penetration depth is unknown, use any of fixed mesh in the best case may only localize the unknown boundary of the contact zone Γ_c(α) between two neighboring mesh points. At the same time, as shown in 8, any perturbation of the parameter a_c > 0 even for one mesh step, can deviate from values of the normal component σ₂₂ of stress on neighborhood of the contact zone. For this reason, the above iteration process will be used with the remeshing (regridding) algorithm described below. The main distinguished feature of this algorithm is that the total number of mesh points remain constant, which permits to deal with the stiffness matrix with constant dimension on each iteration , m=1,2,3, …. The starting point of this algorithm is the situation when the unknown boundary a_c=a_c(α_p) of the contact zone is localized between any two mesh points. Let us assume that and , with boundaries and , two consecutive iterations, corresponding to the parameter α_p. Assume that which means , or equivalently, . Here Γ_c(α_p), with , is the contact zone for α =α_p. Let us introduce the parameter β∈(0, 1) and define the next iteration for the unknown contact zone as follows: (35) We require that . Linearizing this equation we have , δ_m−1, δ_m>0, where and . Hence the free parameter β∈(0, 1) is defined as follows: . Substituting this value in (20) we find . We use this value to construct the new mesh by taking as a new mesh point. Then we continue the step (III) of the above iteration algorithm on this new mesh with the found iteration . This remeshing algorithm highly accelerates the linear convergence of the iteration process, as computational experiments show.

Figure 5. Finite-element mesh (upper mesh) and its part under the indenter (lower mesh).

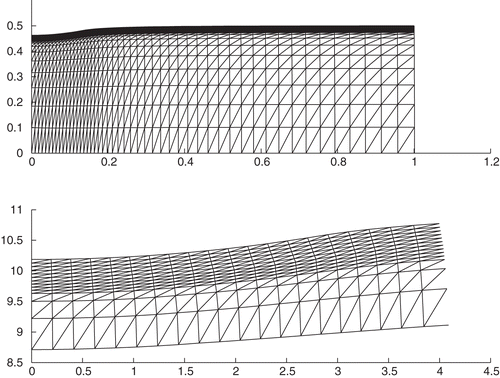
To define an optimal mesh sizes, computer simulation of the quasi-static indentation problem was performed for the power hardening material, given by the plasticity function (10), with the following parameters: E=210 GPa, e₀=0.027, κ = 0.5. The results for two pure elastic (, ) and ten elastoplastic deformation states are given in table 1.

Table 1. Mesh parameters: .

Mesh1: Nx ×Ny= 50×20,	Mesh2: Nx×Ny= 50×30
αk×10^2 cm			GPa			GPa
0.129	2.112	5.117	1.067	1.990	4.823	1.058
0.229	2.706	6.549	2.543	2.645	6.408	2.527
0.50	4.156	8.117	8.288	4.182	8.142	8.236
0.80	5.435	9.282	16.735	5.480	9.321	16.520
1.10	6.560	10.198	27.155	6.544	10.185	26.368
1.40	7.553	10.942	39.071	7.460	10.875	37.631
1.70	8.434	11.563	52.191	8.288	11.463	50.328
2.00	9.191	12.070	66.400	9.075	11.994	64.191
2.30	9.891	12.522	81.607	9.788	12.457	79.062
2.60	10.552	12.933	97.761	10.531	12.921	94.880
2.90	11.160	13.301	114.708	11.193	13.320	111.545
3.20	11.839	13.700	132.392	11.860	13.711	129.040

Let us estimate first the sensitivity (36) of the most important elasticity parameter – elasticity limit e₀, with respect to the mesh size (Mesh1 and Mesh2). As shown in table 1 (bold characters) , , and . In the both meshes, the found approximate values and correspond to the value α₀=0.229×10⁻² of the penetration depth. To estimate this error, the problem was solved with the second choice of the parameters α_k. On the Mesh2, the values , , and of the strain intensity were obtained for the values , , and of the penetration depth, for two pure elastic and one elastoplastic states. Comparing the values and one can conclude that the measurement error (noise) in the values of the penetration depth implies the following relaxation in the obtained values of the strain intensity. This result can be used for estimation of an influence of the noise factor in the measured data α_k to the found (from the numerical solution of the contact problem) value of the strain intensity e_k. Specifically, the results obtained by using the meshes N_x ×N_y= 50×20 and N_x×N_y= 50×30 can be assumed to be same, if the error in the measured data α₀ is about , which is acceptable for an experimental setup (see 19 and references therein).

As table 1 shows, by increasing the number of plastic states the sensitivity of strain intensity e_k decreases. The maximal value of the relaxation parameter for the plastic deformations was found about 1.8%. The same situation was observed for the yield stress: , while . In spite of these, relaxation Δ_Pk between in the calculated values and of the loading force increases from Δ_P0=0.63% to Δ_P10=2.17%, by increasing the number of plastic states.

The deformed profile of the indented specimen and its scaled part under the indenter and near the contact zone, are shown in figure 6.

Figure 6. The deformed profile of the indented specimen and its scaled (enlarged) part under the indenter: E=210 GPa, e₀=0.027, κ = 0.5, α =3.2×10⁻².

6. Parametrization of the inverse problem and least squares approach

First of all, note that in engineering practice an indentation curve cannot be measured continuously in the interval (0, α_K). Therefore, one needs to assume the indentation data , as a finite-dimensional vectors , in R^K+1. The monotone increasing values 0<α₀< α₁<···<α_K of the penetration depth generate the quasi-static indentation. For each α_k, the maximal value of the strain intensity for all finite elements will be denoted by e_k. Such a parametrization naturally leads to the piecewise linear approximation of the stress–strain curve (8). For the pure elastic and first plastic states, this approximation implies: (37) where β₀ = 3G. For kth plastic state, the following approximation formula can be obtained: (38) where is defined as a state discretization parameter, and the angles β_k – slope of the piecewise linear curve (38) (figure 2). The pairs ⟨α_k, P_k⟩ on the plane OαP, correspond to the pairs ⟨e_k, σ_k⟩ on the plane Oe_iσ_i, where . By this way, the inverse problem will be replaced by the problem of identifying the pairs ⟨e_k, β_k⟩ from the finite number of indentation measurements . Due to the monotonicity of the stress–strain curve (8), the set of admissible unknown parameters will be defined as follows: (39) Thus the discrete inverse problem can be formulated as follows: (40) where the unknown parameters and the measured data are (K+1)-dimensional vectors. We assume that an appropriate numerical integration formula is applied to (12), and hence is the finite-dimensional analogue of the nonlinear operator , defined by (11–12).

Evidently a solution of the inverse problem in the sense of equation (40) may not exists, in general. We define a weak solution, according to a least squares approach: find , as a solution of the following minimization problem: (41) where (42) The parametrization scheme (38) shows that the functional (42) needs to be minimized for each , which means the unknown parameters β_k need to be determined on each kth state successively (step by step), by increasing the parameter e_k. For e_i<e₀ only the elasticity modulus E > 0 needs to be found. For the first plastic state the algorithm of the inversion method consists of the following steps:

(i1) Choosing an initial iteration for the unknown parameter β₁ > β₀ and solving the forward problem for given data E, e₀ and .

(i2) Calculating the theoretical value of the loading force, corresponding to the iteration .

(i3) Determining the next iteration by using the conditions: if , then ; otherwise, .

(i4) Determining the mth iteration by using the conditions: if , then .

(i5) Calculating the theoretical value of the loading force, corresponding to the iteration .

(i6) Repeating steps (i4)-(i5) until the error .

The obtained value is assumed to be an approximate solution of the inverse problem (41), in the interval (e₀, e₁) of quasi-static indentation. The piecewise linear approximation of the plasticity function g=g(ξ) in (e₀, e₁) can be obtained by substituting the found value β₁ in equation (37): .

In the above iteration process [steps (i3) and (i4)] the following fact taken into account: increasing the slope β_k corresponds to an increase of rigidity of a material, and as a result, to an increase of the theoretical value of the loading force.

For the second plastic state of indentation the found parameters E, e₀, and β₁ will be used in (38) to determine the next parameter β₂, by repeating the above algorithm. As an initial iteration here one needs to take .

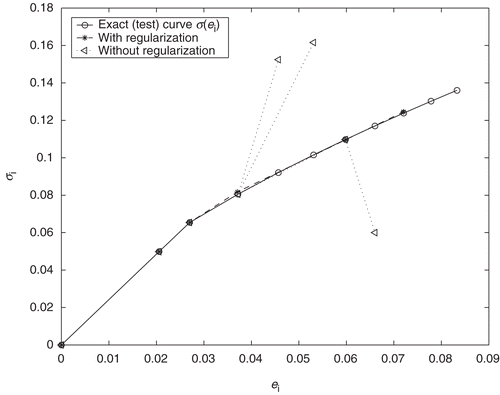
Two distinguished features of the discrete inverse problem need to be emphasized. First, solvability of the inverse problem is a result of monotonicity of the stress–strain curve, which for discrete model (41) means fulfillment of the monotonicity condition (39) for slopes β_k, during the iteration process. Due to closeness of neighboring slopes for the developed plasticity states, and due to computational errors in β_k, in practice, this condition may not be fulfilled. Second, all previously determined parameters e_j, are included, as shows formulas (37–38), in the kth state. Subsequently, computational errors are compounded, and as a result, the second noise factor – computational noise factor arises. By increasing the number of states the influence of this factor will be increased. Hence for small values of state discretization parameters, the inverse problem may become unstable after some state k₀. Illustration of this phenomenon is given by the piecewise linear curve (figure 7), obtained by direct application of the above algorithm. The imitation of the quasi-static indentation process (for two pure elastic and eight plastic states) has been given here by the increasing values α_k=α_k−1+ Δα_k of the penetration depth, where α₀ =1.5×10⁻³ cm corresponds to the last pure elastic deformations. For the corresponding state discretization parameters e_k, the following step sizes have been obtained: . The measured data for the considered inverse problem has been obtained from the quasireal experiment, for the power hardening material with κ = 0.5, e₀=0.027, E = 210 GPa and R = 0.5 cm, by solving the forward problems (1–5), and then calculating the theoretical value of the loading force by (12). The numerical solution of the inverse problem for ϵ_P=10⁻⁶ shows that the iteration process diverges at the second plastic state k₀ = 2 (the left broken line in figure 7). The next increase of the state discretization parameter () again leads to divergence (the second broken line in figure 7). For inversion algorithm converges (the fourth point ☆ on the curve in figure 7). The left broken lines also show that the corresponding slopes β₃ do not satisfy the monotonicity condition (20). The similar behavior has been observed at the fifth plastic state. These results show that the inversion algorithm may not converge for arbitrary values of the state discretization parameters and within the strong fulfillment of condition (30).

Figure 7. Ill-conditionedness of the inverse problem.

In order to guarantee stability and convergence of the inversion method two regularization schemes – relaxation of the monotonicity condition for slopes β_k, and optimization of the state discretization parameters Δe_k – have been added to proposed inversion algorithm. Introducing the relaxation parameter δ_β>0 we will require that the unknown parameters β_k satisfy the following relaxed monotonicity condition (43) Hence, we define the new set of admissible unknown parameters as follows: then instead of , defined by (39).

An optimal choice of the state discretization parameters has been realized as follows. Let us assume that the inversion algorithm converges at k − 1-th plastic state, but diverges at kth plastic state, i.e., neither condition (39) nor the condition (44) hold. In this case, the parameter Δe_k is eliminated from the consideration and taking the new state discretization parameter instead of the parameter Δe_k, the iteration process is repeated anew from the k − 1-th state. This process is repeated until the fulfillment of conditions (43) and (44) and the found step is assumed to be a new state discretization parameter for the kth state. This modification leads to the natural selection of the state discretization parameters, also allows us to minimize the number of indentation measurements. In the considered above example, the optimal values of the state discretization parameters are obtained , and . The relaxation parameter δ_β in figure 7 is assumed to be δ_β=0.3.

Remark 1 Considering the elasticity modulus, E > 0 of the tested material can be determined directly from formula (14). To illustrate this, let us identify E > 0 for the given measured (synthetic) data , which was obtained from the numerical solution of the elastic contact problems (1–5), for given E=210 GPa. Substituting the numerical solution of the contact problems (1–5) with E = 1 in the right hand side of (14) yields: P₀=0.804 ×10⁻³ GPa. By (14) , and hence E⁽⁰⁾ =209.850 GPa. The relative error ϵ_E=|(E−E_h)/E| is about 0.07%, which shows high accuracy of the algorithm of finding the elasticity modulus. ▪

Remark 2 Determination of the elasticity limit e₀ has been performed by using the inequality , where E⁽⁰⁾ is the already found elasticity limit, and E⁽¹⁾ the value of the elasticity limit corresponding to the value of the indentation depth. By increasing the value there arises such a value , for which the above inequality does not hold. The corresponding value e₀=max_Ωhe_i(u), obtained from the numerical solution of problems (1–5), is assumed to be the elasticity limit. This algorithm shows two indentation data for pure elastic deformations is enough for determination of the elasticity limit e₀.

7. Numerical verification of the inversion method for noise free and noisy data

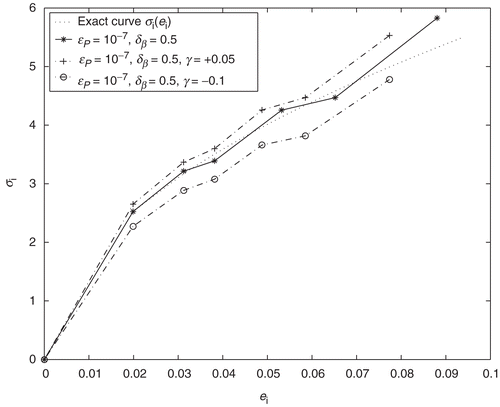
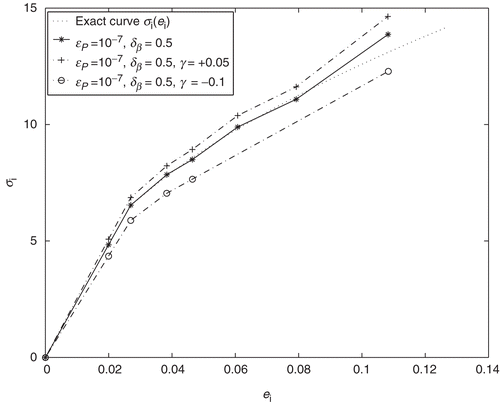
In experiments, the indentation curve can only be given with some measurement error 17, 19, as the finite number of measured data , . Here is an exact data corresponding to kth indentation step. In this case, in addition to the parameters ϵ_P>0 and δ_β>0, the stability of the inversion algorithm with respect to the noise factor γ > 0 also arises. Two types of power hardening materials (with elasticity parameters E=110 GPa, e₀=0.020 and E=210 GPa, e₀=0.027) are selected to examine the proposed inversion method. The indentation curves for these materials, obtained by from the numerical solution of problems (1–5) with r₀=0.5, κ = 0.5, are shown in figure 8. The noisy data have been generated by taking γ = 0.05 and γ =−0.1. All these data have been then used as a synthetic data for identification of the curve . The results are shown in figures 9 and 10. For noise free data , the reconstructions of the stress–strain curve have enough accuracy, in the both cases. Thus, the relative error in the reconstructed curve, for the first material, is about ϵ_σ=3%, except the fifth plastic state (the last ☆-point in figure 9). At this state the relative error was ϵ_σ=10%. This is due to the compounded errors in (38) from previous states, as was suggested above.

Figure 8. Noise free and noisy indentation curves.

Figure 9. Identification of the stress–strain curve: E=110 GPa, e₀=0.020.

Figure 10. Identification of the stress–strain curve: E=210GPa, e₀=0.027.

For the second type of power hardening material, the reconstruction of the stress–strain curves from noise free and noisy data, given in figure 8 (bottom curves), are plotted in figure 10. In the case of the noisy data, an accuracy of the reconstructed curve for the first to fourth plastic states is about ϵ_σ=1%, and ϵ_σ=6%, for the fifth plastic state. For the noisy data accuracy of the reconstruction decreases, in particular in the beginning plastic states. For the noise factors γ =0.05;−0, 1 the relative errors rise up to ϵ_σ=12% and ϵ_σ=7%, for the first and second materials, respectively.

Note that, the noisy data also can change the optimal selection of the state discretization parameters, as shows the examples.

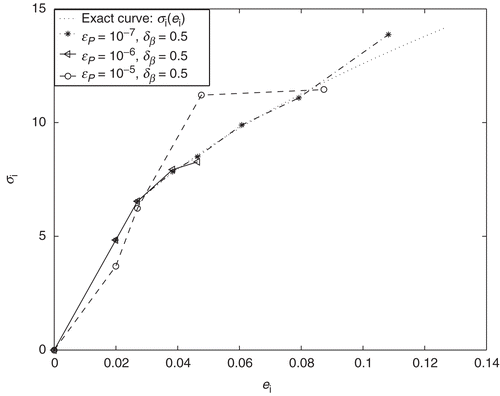
In the sense of accuracy and stability, here and in the previous example the similar behavior of the identified curves can be observed. This is due to the same stopping and relaxation parameters in the both cases: ϵ_P=10⁻⁷, δ_β=0.5. The optimal value ϵ_P=10⁻⁷ of the stopping parameter in (44) was selected from series of computational experiments, taking into account the sensitivity of the solution of the nonlinear equation (11) (or (40)) with respect to the right hand side . An increase of the parameter ϵ_P>0 will naturally lead to the loss of accuracy. To analyze this situation, the identification problem was solved for the noise free data obtained from the synthetic data given by upper solid line in figure 8. The identified stress–strain curves corresponding to the increasing values 10⁻⁷, 10⁻⁶, 10⁻⁵ of the parameter ϵ_P are shown in figure 11. Comparing the identified values σ₂ (corresponding to the second plastic state) obtained for these three cases, one can clearly observe from figure 11 that by increasing the stopping parameter an accuracy of the identified curves decreases.

Figure 11. An influence of the stopping parameter ϵ_P>0 to identifiability.

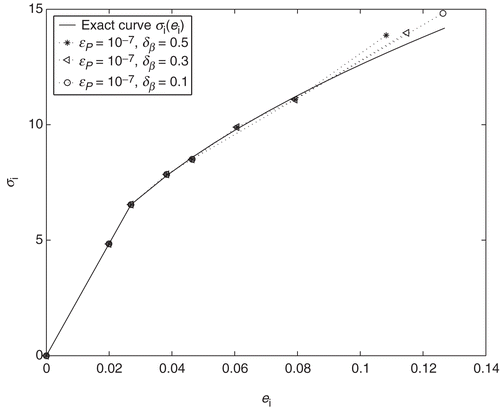
Let us analyze finally an influence of the relaxation parameter δ_β used for stabilizaton of the above identification algorithm. For this aim, the above identification problem was solved for three various values , , of the relaxation parameter. The results are shown in figure 12 (Note that the identified curves –⋆–, corresponding to the parameter , here and in figure10, are the same). Thus, in the case of the large relaxation parameter , the following optimal selection of state discretization parameters were obtained: , , . In the case of small relaxation parameter (curve −○− in figure 12) only the first two state discretization parameters remain the same: and . The third parameters is essentially different from: . The large optimal value of the state discretization parameter is due to that the small relaxation parameter requires almost strict fulfillment of the monotonicity condition (39), and as a result, large steps for the state discretization parameters e_k, in order to guarantee the stability.

Figure 12. An influence of the relaxation parameter δ_β to identifiability.

The obtained results show that the presented inversion algorithm is also feasible in the presence of a noise factor .

8. Conclusions

The inversion method for identifying the stress–strain curve from the measured indentation loading curve, during the quasi-static spherical indentation has been presented. An analysis of the ill-conditionedness of the considered inverse problem has been carried out theoretically, as well as computationally. The method is based on the FE discretization of the contact problem and parametrization of the stress–strain curve. The presented algorithm of optimal selection of state discretization parameters is a new and natural regularization algorithm for such a class of inverse diagnostic problems. The inversion method with this regularization algorithm permits one to not only determine effectively the stress–strain curve from the measured loading curve, but also suggests how one needs to simulate and select the limited number of experimental data , in order to minimize it. The demonstrated numerical results for different engineering materials show that the presented inversion method allows to determine the stress–strain curve σ_i=σ(e_i) from the noise free, as well as noisy indentation loading curve, with high accuracy.

Finally, it should be emphasized that this study mainly focuses on the theoretical and computational aspects of the inversion method for considered here indentation problems. Further applications of the method, by taking into account such a physical and engineering aspects as geometrical nonlinearity, elastic deformations of the indenter, use of the unloading part of the indentation curve, will be especially useful and will be an essential part of the future research.

Acknowledgements

The author is grateful to Dr Z. Muradoglu for the assistance in providing the computational experiments. The author also gratefully thanks the referees for valuable suggestions which improved the revised version of the manuscript.

 This work was partially supported by the Scientific and Technical Research Council of Turkey (TUBITAK).