Abstract
A crucial problem that occurs when estimating physical parameters from experimental data is the computation of reliable uncertainty bounds for the estimated parameters, while accounting for uncertainty in the model and data. We introduce a new numerical method that contributes to the solution of this problem. We show how to deal with uncertain nuisance parameters located within prior intervals. The method advocated in this article makes it possible to detect the absence of solution when the model hypotheses are inconsistent with the data. An analysis of the sensitivity of estimated uncertainty bounds to the nuisance parameters is also conducted. These features are illustrated with actual data collected on a thermal device used to estimate simultaneously the conductivity and diffusivity of materials.
Nomenclature
| = |
Model quantities
| a | = | PVC thermal diffusivity |
| ek | = | thickness of the k-th layer |
| fi | = | i-th excitation frequency |
| h | = | generalized heat exchange coefficient |
| H | = | transfer function vector |
| p | = | parameter vector to be identified, in prior domain |
| q | = | nuisance parameter vector, in prior domain |
| R | = | thermal resistance of the glue |
| Rk | = | thermal resistance of the k-th layer |
| s | = | Laplace variable |
| si | = | sensitivity coefficient with respect to qi |
| = | temperature on the rear side of the k-th quadrupole | |
| = | output temperature | |
| yi | = | measurement datum at frequency fi |
| [y] | = | complex interval data vector |
| = | thermal impedance of the k-th quadrupole | |
| λ | = | PVC thermal conductivity |
| ξ | = | relative position of the thermocouple in the rear layer |
| τk | = | Fourier time of the k-th layer |
| = | flux on the rear side of the k-th quadrupole | |
| = | output flux |
Set estimators
| = | set of acceptable values of | |
| = | section of | |
| Π | = | projection of |
| ϵ | = | maximum width of the boxes to be bisected |
Interval symbols
| [f](·) | = | inclusion function for a function f(·) |
| [x] | = | interval |
| [x] | = | interval vector (box) |
| c[x] | = | centre of the interval [x] |
| = | relative uncertainty of the interval [x] | |
| w([x]) | = | width of the interval [x] |
Other quantities
| j | = |
1. Introduction
Estimating physical parameters generally amounts to fitting a theoretical model to experimental data. Even if this model is unavoidably a mere approximation of the actual physical process, many other sources of approximation should be considered while evaluating the values of the parameters of the model and the uncertainty. Repeated experiments and statistical inference are commonly used techniques for quantifying parameter uncertainty. However, the validity of the underlying statistical hypotheses and the resulting confidence regions are often questionable. Moreover, deterministic model errors cannot be described by random variables. Finally, the model often involves additional parameters called nuisance parameters whose values are usually assumed to be known, but are actually also uncertain.
The aim of this article is to present a guaranteed method to identify the parameters of interest while accounting for all sources of uncertainty in both the model and experimental data. We shall characterize the set of all acceptable values of the parameters to be identified within a new framework where errors are assumed bounded with known bounds but otherwise unknown. This is called bounded-error or set membership estimation (see e.g., Citation1–4 and references therein). The size of the set computed will be a straightforward measure of the uncertainty associated with the estimated parameters. In the same framework a specific method will be derived to take into account the uncertainty associated with the nuisance parameters, when only intervals to which they belong are provided. The increase in the set estimate with the uncertainty in each nuisance parameter will quantify the sensitivity to this nuisance parameter of the uncertainty in the parameters of interest.
As an illustration of the methodology, we shall address the simultaneous estimation of the thermal transport properties of materials. Several measurement techniques can be used for this purpose. Besides the transient plane source approaches Citation5–9, the joint estimation of the conductivity and diffusivity of a sample can be achieved by periodic heating, with a laser source Citation10, or using a small temperature modulation in the sample Citation11,Citation12. In these cases, parameter estimation is usually carried out while assuming some noise statistical properties and neglecting the uncertainty in the nuisance parameters. The limitation of such an approach has been pointed out in Citation12 as the method developed could not derive acceptable values for the diffusivity, when the sample is thin the physical uncertainty in the nuisance parameters, e.g., the resistance of thermal contact could no longer be neglected.
In this article we shall illustrate the performance of our approach on the simultaneous estimation of the diffusivity and conductivity of materials by the periodic method described in Citation12. We shall first compare it with classical least-square identification, while assuming that the values of the nuisance parameters are known. We shall then extend this method to consider also the uncertainty associated with the nuisance parameters. Finally, we shall show how this new technique makes it possible to analyse the influence of the uncertainty in each nuisance parameter on the estimates of the parameters of interest. This sensitivity analysis allows one to draw suggestions for improving the performance of the experimental set-up.
Section 2 briefly describes the experimental apparatus and its theoretical model. The framework of bounded-error set estimation is then explained in section 3. The resulting estimates and the sensitivity analysis will be presented in section 4. The main symbols used in this article are shown in nomenclature.
2. Experimental procedure and its model
In this section, we shall briefly present the experimental set-up and the theoretical model used in this article in order to illustrate the capabilities of the bounded-error estimation technique. Note that other experimental procedures for the simultaneous estimation of thermal transport properties could benefit from a similar treatment.
2.1. Experimental procedure
The experimental procedure is similar to the one described in Citation12. The sample under study is glued within a metallic rack. The front side of the rack, made of brass, is also fixed to a heating device. The rear side, made of copper, is in contact with air at ambient temperature. To reduce lateral heat losses, radiative shields are used. The heating sequence consists of five sinusoids with frequencies f1 = 0.781 mHz, f2 = 1.562 mHz, f3 = 3.125 mHz, f4 = 6.25 mHz, and f5 = 12.5 mHz.
The temperatures Tout and T0 of the rear and front sides, respectively are measured during 85 min with thermocouples, whose outputs are amplified, sampled at 100 Hz, low-passed with a digital Hanning filter with a cut-off frequency of 0.2 Hz, and then under-sampled at 0.4 Hz to avoid aliasing. The Fourier transforms of the two measured temperature signals are then computed, and their ratio at each frequency fi provides a realization of the experimental yi:
(1)
where ℓ stands for the realization index. The experimentation is repeated 30 times, to collect for each frequency fi a set of 30 realizations
of the random complex datum yi.
2.2. Knowledge-based model
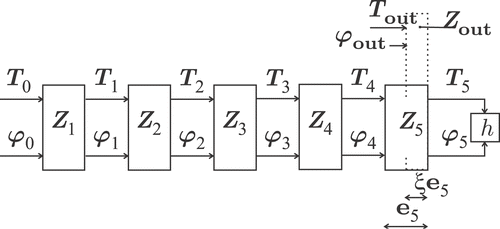
The system under study is modeled with quadrupoles Citation13, i.e., matrices with two inputs and two outputs. Let be the Laplace transforms of the temperature and flux at the rear side of the k-th layer of homogeneous material. With this k-th layer is associated a quadrupole () whose impedance
is given by
so that
where the thermal resistance Rk and Fourier time τk depend on the thickness ek of the layer, and on the conductivity and diffusivity of the material. The conductivity λ and diffusivity a of the sample can then be derived from
(2)
The glue is assumed to have no inertia (τ2 = τ4 = 0) and the two glue layers are assumed to have the same thickness: R2 = R4 = R. The front temperature/flux pair
is then related to the ambient temperature/convective flux pair (T5, ϕ5) by
(3)
The copper layer between the second thermocouple and the convection exchange surface will also be modeled with a quadrupole
in order to introduce the convection losses and the position ξe5 of the thermocouple, see . The output temperature and flux are then given by
(4)
with
(5)
Heat transfer between the rear plate and air at ambient temperature is modeled by
(6)
where h is the generalized heat surface exchange coefficient. Although the value of h depends on several parameters such as the sign of the flux, the flow velocity, or the surface tilt angle, one does not know how to quantify it when the surface temperature varies as a sinusoidal function. As usual when dealing with heat transfers at ambient temperature, we shall assume its value constant. Using equations (3–6), we evaluate the complex transfer function at the i-th fi:
(7)
The quantities Hi defined by (7) depend on several uncertain parameters. First, the thermal characteristics of the copper, brass and the sample cannot be measured without destroying the device because of the glue; their prior uncertainty is then only assumed to be in the range of values found in the literature. Second, the thermal conductivity of the glue as provided by the manufacturer is inaccurate. Finally, the thickness of each layer is measured with uncertainty.
2.3. Parameters to be estimated
We shall group the parameters to be estimated in the parameter vector p
(8)
Let
be the prior domain for p. As the estimation technique to be presented can easily deal with large prior domains, we take
m2KW−1 × [1, 30] s1/2 to encompass all possible values of R3 and
.
2.4. Nuisance parameters
The remaining parameters (which are of no interest) are gathered in a vector q of nuisance parameters
(9)
The prior domain for q is taken as the Cartesian product of the prior intervals
describing the uncertainty about each of the nuisance parameters qi,
. These intervals are given in .
Table 1. Prior domains of the nuisance parameters
The objective is to estimate the parameter vector p. A classical point estimation method and the results obtained in this context Citation14 are first introduced. We then present the results obtained by bounded-error estimation. First we assume that the nuisance parameter vector q takes some given value q* inside its prior domain . Then we relax this hypothesis by considering q as an uncertain variable that can take any value in
.
3. Parameter estimation
3.1. Point estimation
Consider a single frequency fi, and the corresponding model output . With each realization
is associated a realization
of the output error ei:
In a stochastic framework, the maximum-likelihood approach makes it possible to derive a criterion to be optimized to estimate
based on hypotheses on the probability density function of the data. Under the usual Gaussian assumptions, the maximum-likelihood estimator for p boils down to the least-square estimator, which minimizes the quadratic norm of the output error
(10)
with respect to p, while the nuisance parameter vector q is assumed to be known Citation12.
For the set-up and data considered here, we assume as in Citation14 that q is equal to
(11)
Because the model employed is nonlinear in its parameters, the minimization is usually performed by iterative search. We used here a Levenberg–Marquardt algorithm to minimize (10). The resulting point estimate is
(12)
An asymptotic uncertainty domain associated with this estimate is classically derived as the ellipsoid
(13)
where F is the Fisher information matrix. This ellipsoid corresponds to a 95% confidence level.
This result can be questioned for three reasons. First, the uncertainty associated with the value q1 has been neglected. In order to take into account this disturbance, Fadale Citation15 has proposed an extended maximum-likelihood estimator in which the above nuisance parameters are modeled as normal random variables with known variance. The uncertainty associated with the identified parameters is then derived from the asymptotic variance of the estimator. Unfortunately, the prior distribution of the nuisance parameters is usually unknown. In the general case, only a range of values is available. Second, the underlying Gaussian hypothesis may not be realistic. Last, the results are obtained with no guarantee, as this local search method may get trapped near a local minimum or stop before reaching the actual global minimum. The method to be presented in the next section will permit to bypass these obstacles.
3.2. Bounded-error estimation
Instead of assuming a probability density function for ei, bounded-error estimation only requires bounds for the possible values of each datum yi. These bounds are here obtained as follows. Define the complex interval [yi] associated with the frequency fi as
with
respectively the real and the imaginary parts of the interval [yi]. This complex interval thus takes into account the variability of the datum yi, and no other assumption on the distribution of the data will be needed. In the following we shall consider real and interval vectors and matrices and denote by
the complex interval vector whose i-th entry is [yi]. H stands for the vector of the model outputs Hi.
We shall say that is acceptable if the model outputs
, are consistent with the data given their uncertainty, i.e.,
. The set
(14)
is a bounded-error estimate for
. Characterizing it thus amounts to estimating all the acceptable values of the nine-dimensional vector
. However, this turns out to be hardly tractable because the complexity of the branch-and-bound algorithm to be used is exponential in the dimension of the vector to be estimated Citation16. To overcome this difficulty, a new algorithm has been developed in order to estimate p alone while considering that q can take any value inside the prior domain
. To compare our results with the point estimate (12), we shall first assume as in section 3.1 that the nuisance parameter vector is equal to q*. In a second part, we shall relax this hypothesis and consider that q can take any value inside
.
3.3. Estimation of p with a known value of the nuisance parameter vector
Assume that the value q* for the nuisance parameter vector q is known. The set
(15)
then contains all values of p such that
is acceptable. Let h be the function from the bidimensional real field
to the five-dimensional complex field
such that
. With this notation,
(16)
(17)
Characterizing Σ(q*) requires the computation of the reciprocal image of the set [y] by the function h. It is thus a set-inversion problem Citation17.
3.4. Estimation of p for an uncertain nuisance parameter vector
Assume now that the value of the nuisance parameter vector q is uncertain. Instead of characterizing the 9-dimensional set , which would once again be a set-inversion problem, we shall estimate the set Π of all the acceptable parameter vectors p under the assumption that q belongs to its prior domain
(18)
While Σ(q*) is a cut of
at
, Π is the projection of
onto p-space (). The inclusion
illustrates the fact that the uncertainty on q increases the uncertainty associated with the estimation of p.
Figure 2. The sets to be characterized: the solution set , its projection Π on
and a section Σ(q*) corresponding to a point value
.
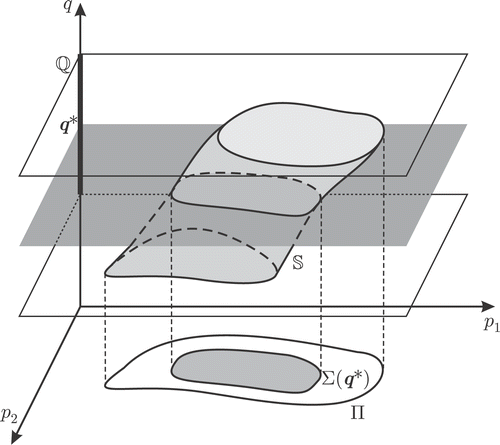
This projection strategy gives up the estimation of nuisance parameters in order to facilitate the computation of a set estimate for the parameters of interest.
3.5. Implementation of the set-membership estimation
3.5.1. Outer enclosure
To provide a guaranteed estimation of a set that may be either Σ(q*) defined by (15) or Π defined by (18), two sets
and
such that
are computed. Thus, any value of p that belongs to the inner approximation
of
is proved to be consistent with the experimental data, while any value that lies outside the outer approximation
is proved to be inconsistent. The projection of the outer approximation
onto the i-th axis provides a guaranteed uncertainty interval estimate
for the i-th parameter pi. In the following, we will equivalently characterize this interval using its centre
and its relative uncertainty
, where
is the width of the interval. The width of the interval vector [p] is then defined as
.
3.5.2. Interval analysis
To guarantee set enclosure, and
are computed using interval analysis Citation17–19. Interval analysis provides a set of rules extending point arithmetics to intervals, and allowing the construction of an interval counterpart [f](·) to a real function f (·), such that for a given [x],
. The inclusion function [ f ](·) makes it possible to compute a reliable outer approximation of the set
, while other numerical approaches only perform an evaluation of the image of a discrete set of values in [x]. It is therefore possible, in a single interval computation, to test whether the outer approximation
of the image of an interval vector (or box) [x] by the function f (·) is included in a given interval. Consider the set-inversion problem where
and the two following statements
(19)
(20)
If equation (19) is satisfied, [p] belongs to the inner approximation of
(and of course to its outer approximation
). If equation (20) is satisfied, [p] has a void intersection with
and
. The algorithm SIVIAP starts from the search box
and iteratively splits it into subboxes whenever neither equation (19) nor (20) is satisfied. The tests are then applied to these subboxes. To ensure the termination of such a branch-and-bound algorithm, a parameter ϵ defining the maximal size of the undetermined boxes is to be tuned by the user. The value chosen for ϵ will realize a trade-off between the accuracy of the enclosure and the time and memory required to compute it. The reader may consult Citation17 for the details of SIVIAP and Citation20 for an illustration.
3.5.3. Specificity of the projection algorithm
If equations (19) and (20) are enough to determine guaranteed outer and inner approximations and
for the section Σ(q*) defined by equation (17), to compute a guaranteed enclosure for the projection Π defined by equation (18) one requires a specific routine that will detect whether, for a given box [p]
(21)
or
(22)
If equation (21) is satisfied, then [p] belongs to the inner approximation of Π (and of course to the outer approximation Π). If (22) is satisfied, then [p] has a void intersection with Π and Π. Here again, the algorithm PROJECT Citation21 starts from the search box
and iteratively splits it into subboxes whenever neither equation (21) nor (22) is satisfied. The tests are then applied to these subboxes unless
. To select a candidate value for q, local search techniques such as Monte Carlo simulations can be employed; we used here an alternative interval approach, called INSIDE Citation21.
4. Results and discussion
In this section we analyse the bounded-error estimates of the conductivity and diffusivity of the material sample. In the first part, we neglect the uncertainty associated with the nuisance parameters and compare the results obtained with the set-inversion algorithm to the least-square point estimates. In the second part, we take into account the uncertainty associated with the nuisance parameters and describe the results obtained with the set-projection algorithm. We finally draw some suggestions to improve the set-up accuracy from a study of the influence of the uncertainty of each of the nuisance parameters on the estimates of the sample characteristics. The sample under study is made of PVC. The literature suggests that m2K W−1 and
, which correspond to
m2s−1 and λ ∈ [0.160, 0.182] Wm−1K−1. All the numerical computations have been performed on a Pentium IV at 1.7 GHz.
4.1. Nuisance parameters with known values
In this subsection, it is assumed that the values of the nuisance parameters are known. The nuisance parameter vector q will be taken equal to its nominal value q1 as chosen in Citation14 and defined by (11). In particular, note that q3 had been arbitrarily taken as = 0, which amounts to assuming that the thermal contact resistance is negligible. Taking
= 5 means neglecting the convective heat flows on the rear face. We shall question these hypotheses later on.
We first test whether the point estimate is consistent with our error bounds. In the real and imaginary parts of the entries
of
as a function of fi is indicated by circles, for i varying from 1 to 5. The rectangles stand for the pattern imposed by [y].
Figure 3. Model output (O) and
(+) and pattern imposed by the interval data [yi] (rectangles) as functions of fi.
![Figure 3. Model output (O) and (+) and pattern imposed by the interval data [yi] (rectangles) as functions of fi.](/cms/asset/ed50f17b-426c-4b73-8077-81b545325b20/gipe_a_219112_f0003.gif)
As , the couple
obtained through classical least-square minimization is not consistent with the interval datum [y1]. This result can be confirmed using the algorithm SIVIAP that computes an outer approximation of the set
defined by (15). In 2.5 s for ϵ = 0.02 SIVIAP indicates that
, proving that
is empty : there exists no p in
that is consistent with [y] under the hypothesis
. This result illustrates a distinctive feature of guaranteed bounded-error estimation which makes it possible to prove that a given problem has no solution. Given the modeling hypotheses, the numerical values chosen for the nuisance parameters and the error bounds, it is not possible to find any acceptable value for the parameter vector p. Note that with the usual estimation methods based on local iterative optimization, such an inconsistency could not be detected.
Two reasons may explain why there is no solution: the first one is relative to the data and error hypotheses (the interval [y1] may be too small, or there may exist outliers); the second one is relative to modeling hypotheses: inconsistency may result of erroneous physical assumptions (the hypotheses leading to may not be realistic).
Assume for instance that the value used for the heat exchange coefficient h is taken as the upper bound 10 of the prior interval, instead of the lower bound 5, and consider the following value of the nuisance parameter vector
Now, the least-square estimate is
and the asymptotic 95% confidence region given by (13) is depicted in . The model outputs
are represented in by crosses (+), and the extended vector
turns out to be acceptable. These hypotheses are thus consistent with the model and the experimental data, and the estimate
becomes acceptable in the bounded-error context. A physical interpretation is that the convective heat flow cannot be neglected on the rear face for the nominal value of the other nuisance parameters. From now on, we shall use q2 as the nominal nuisance parameter vector.
Figure 4. Estimate of the set Σ(q2) obtained with h=10: inner approximation (black) and outer approximation
(union of the black and grey boxes). The least-square estimate
and its ellipsoidal confidence region are also depicted.
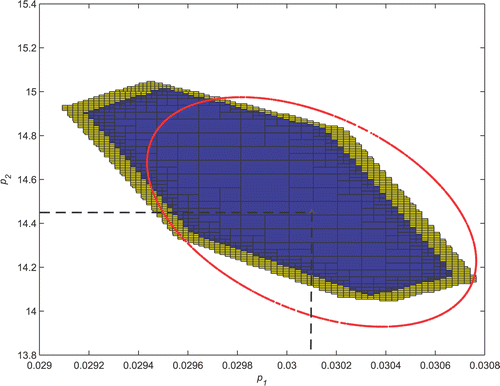
Consider now the set . In 7.8 s for ϵ = 0.001, SIVIAP computes two nonempty sets
and
(). Now
is proved to be consistent with the data as it belongs to
. Compare the uncertainty domain described by
and
, and the uncertainty domain
associated with
obtained by minimizing (10) in .
and
are quite close, and fairly comparable to this ellipsoidal region. The projection of
onto the p1 and p2 axes provides an outer approximation of the uncertainty interval associated with each parameter:
K W−1,
, so
(23)
Using (2), we can now compute an outer approximation for the set of all acceptable values for the diffusivity a and the conductivity λ of the sample, such that
In summary, h = 5 is invalidated, while to h = 10 correspond some acceptable models. An alternative way to check the consistency of the value to be chosen for h consists of extending the parameter vector to be estimated to the triple (p1, p2, h), and projecting the resulting estimated set onto h-space to determine the interval of acceptable values for h. SIVIAP then provides h∈[5.3, 10], which confirms that h = 5 is inconsistent with our other hypotheses. The hypothesis , which means that the presence of glue is neglected, has been maintained in the definition of the set
. Obviously, as the resistance of the glue R is proportional to its thickness, which has been measured using a microscope, and proved to be larger than 30 × 10−6 m, this assumption corresponds to a simplified model. The same approach as described earlier can be used to estimate the acceptable values of the extended parameter vector
. SIVIAP confirms that R = 0 is not inconsistent with the data as the projection onto the R-space of the estimated inner set is
m2K W−1.
Until now it was assumed that the values for the nuisance parameters were known. We have just begun to relax this assumption in order to take into account the uncertainty associated with one nuisance parameter at a time. We shall now consider the uncertainty associated with all the nuisance parameters simultaneously.
4.2. Uncertain nuisance parameters
This section describes a methodology for dealing with uncertainty in the nuisance parameters. As already mentioned, the problem is to estimate the projection Π defined by equation (18) of the set onto p–space. We know that Π is not empty, as
is a nonempty inner approximation of Π (). PROJECT Citation22 confirms this result by providing non-empty inner and outer approximations of Π (). The interval hull for Π is
so
(24)
Figure 5. Inner approximation (black) and outer approximation Π (union of black and grey boxes) of the set Π obtained by PROJECT for ϵ=0.01 in 82 s.
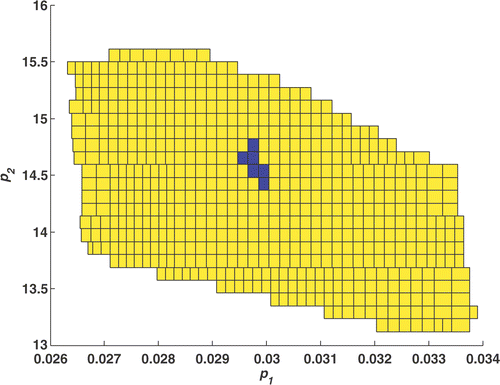
Using (2), we can then compute a parameter uncertainty interval for the diffusivity coefficient a and the conductivity coefficient λ of the sample
Note that the uncertainty associated with the estimation of p1 and p2 has increased as the size of is larger than that of
[compare (24) with (23)]. For ϵ=0.01, the distance between the inner and outer approximations remains large. More accurate results could be obtained by decreasing ϵ, at the cost of an increase in computing time.
It is interesting to study the influence of each nuisance parameter on the uncertainty of the parameters of interest. We shall show how set projection makes this sensitivity analysis possible.
4.3. Influence of nuisance parameter uncertainty
In this section we quantify the contribution of each nuisance parameter qi to the uncertainty on p. For this purpose, we shall study the variation of the volume of the set of all acceptable values of p that results from accounting for the uncertainty associated with qi, while all the other nuisance parameters are taken equal to their nominal value.
For a given nuisance parameter qi, define its sensitivity as
(In the two-dimensional case considered here, the computation of volumes becomes that of surfaces.) The denominator of this expression corresponds to the volume of the set obtained when all the nuisance parameters are set equal to their nominal value. Πi in the numerator is the set obtained when all the nuisance parameters are set equal to their nominal value except for qi, which may take any value inside . As any Πi satisfies
, we have
. If si is close to one, taking into account the uncertainty associated with the nuisance parameter qi does not significantly worsen the uncertainty on the estimate of p. To the contrary, a large value of si indicates a nuisance parameter qi for which reducing uncertainty would be beneficial. In practice, si may only be enclosed in
where the volume of each set is obtained by summing the volumes of each of its constitutive boxes. represents [si], i = 1, … ,7, obtained by computing inner and outer approximations of Πi for ϵ=0.02.
Table 2. Influence on the uncertainty on the parameters of interest of the uncertainty associated with each nuisance parameter
When i differs from 4 and 5, , which means that the estimated parameters are weakly sensitive to the uncertainty on the nuisance parameter qi. On the other hand, both copper parameters have a much more detrimental effect on the volume of the resulting set estimate, although showed that the relative inaccuracy for the copper parameters was the lowest one. This may be explained by the location of the copper layer on the rear side, that governs heat transfers, and suggests that the parameters of the rear layer should be made more accurate. This can lead designers to either identifying these nuisance parameters prior to the experiment or selecting another material whose characteristics are better known.
5. Conclusions and perspectives
The methodology presented in this article addresses the problem of estimating parameters in the presence of model uncertainty in a radically new way. One of its striking features is its ability to prove the consistency or inconsistency of modeling hypotheses. This is due to the unique properties of interval analysis. The experimental procedure considered here was meant as an illustration, and the technique is of course much more general. Here, an analytical expression of the model output as a function of the parameters was available. In the future, cases where the model is defined by a differential equation for which no analytical solution is available will also be considered. The tools for guaranteed integration should be helpful in this context.
References
- Milanese, M, Norton, J, Piet-Lahanier, H, and Walter, E, 1996. Bounding Approaches to System Identification. New York, NY: Plenum Press; 1996.
- Belforte, G, Bona, B, and Cerone, V, 1990. Parameter estimation algorithms for a set-membership description of uncertainty., Automatica 26 (5) (1990), pp. 887–898.
- Norton, JP, 1994. Special issue on bounded-error estimation: Issue 1., International Journal of Adaptive Control and Signal Processing 8 (1) (1994), pp. 1–118.
- Norton, JP, 1995. Special issue on bounded-error estimation: Issue 2., International Journal of Adaptive Control and Signal Processing 9 (1) (1995), pp. 1–132.
- Gustafsson, SE, 1991. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials., Review of Scientific Instruments 62 (3) (1991), pp. 797–804.
- Karawacki, E, Gustavsson, M, and Gustafsson, SE, 1994. Thermal conductivity, thermal diffusivity and specific heat of thin samples from transient measurements with hot disk sensors., Reviwe of Scientific Instruments 65 (1994), pp. 3856–3859.
- Karawacki, E, Gustafsson, SE, and Khan, MN, 1979. Transient hot-strip method for simultaneously measuring thermal conductivity and thermal diffusivity of solids and fluids., Journal of Physics D: Applied Physics 12 (1979), pp. 1411–1421.
- Karawacki, E, Gustafsson, SE, and Khan, MN, 1981. Determination of the thermal-conductivity tensor and the heat capacity of insulating solids with the transient hot-strip method., Journal of Applied Physics 52 (4) (1981), p. 2596.
- Karawacki, E, Gustafsson, SE, and Chohan, MA, 1986. Thermal transport studies of electrically conducting materials using the transient hot-strip technique., Journal of Physics D: Applied Physics 19 (1986), pp. 727–735.
- Thoen, J, and Glorieux, C, 1997. Photoacoustic and photopyroelectric approach to calorimetric studies., Thermochimica Acta 304–305 (1997), pp. 137–150.
- Mattei, S, and Tang Kwor, E, 2000. A new periodic technique for thermal conductivity measurement., High Temparture-High Pressures 32 (1) (2000), pp. 3–8.
- Boudenne, A, Ibos, L, Gebin, E, and Candau, Y, 2004. A simultaneous characterization of thermal conductivity and diffusivity of polymer materials by a periodic method., Journal of Physics D: Applied Physics 37 (2004), pp. 132–139.
- Wang, H, Degiovanni, A, and Moyne, C, 2002. Periodic thermal contact: a quadrupole model and an experiment., International Journal of Thermal Sciences 41 (2002), pp. 125–135.
- Tang-Kwor, E, 1998. Contribution au développement de méthodes périodiques de mesure de propriétés thermophysiques des matériaux opaques.. Créteil, France: University Paris XII Val-de-Marne; 1998, PhD dissertation.
- Fadale, TD, Nenarokomov, AV, and Emery, AF, 1995. Uncertainties in parameter estimation: the inverse problem., The International Journal of Heat and Mass Transfer 38 (3) (1995), pp. 511–518.
- Jaulin, L, and Walter, E, 1993. Guaranteed nonlinear parameter estimation from bounded-error data via interval analysis., Mathematics and Computers in Simulation 35 (2) (1993), pp. 123–137.
- Jaulin, L, Kieffer, M, Didrit, O, and Walter, E, 2001. Applied Interval Analysis. London: Springer-Verlag; 2001.
- Hansen, ER, 1979. Global optimization using interval analysis: the one-dimensionnal case., Journal of Optimization Theory and Applications 29 (3) (1979), pp. 331–344.
- Moore, RE, 1966. Interval Analysis. Englewood Cliffs, NJ: Prentice-Hall; 1966.
- Braems, I, Berthier, F, Jaulin, L, Kieffer, M, and Walter, E, 2001. Guaranteed estimation of electrochemical parameters by set inversion using interval analysis., Journal of Electroanalytical Chemistry 495 (1) (2001), pp. 1–9.
- Jaulin, L, Braems, I, and Walter, E, 2002. "Interval methods for nonlinear identification and robust control.". In: Proceedings of 41st IEEE Conference on Decision and Control. Las Vegas, USA. 2002. pp. 4676–4681.
- Braems, I, 2002. Méthodes ensemblistes garanties pour l'estimation de grandeurs physiques.. Orsay, France: Université Paris-Sud; 2002, PhD dissertation.