A homotopy-projection method for the parameter estimation problems

Abstract

A homotopy-projection method is proposed for the parameter estimation problems of partial differential equations. To overcome the local convergence of traditional iterative methods, the homotopy method and Tikhonov regularization combine to form a new and widely convergent method. Additionally to that, projection method is introduced to fulfill the constrains described by a closed and convex set. As a practical application, the parameter estimation problem of an elliptic equation is solved. Numerical results show the method's effectiveness.

Keywords:

• Homotopy-projection method
• Tikhonov regularization
• Parameter estimation problem

1. Introduction

The problem of determining the parameter a(x) is reduced to solving the nonlinear ill-posed operator equation (1) where with domain . Here, is not necessarily a maximal domain of definition, but rather a set of interest whose definition might include certain features of the solution one is interested in. Throughout this article we will assume that is closed and convex.

We restrict our attention to Hilbert spaces and with inner products and norms , respectively; they can always be identified from the context in which they appear.

Since is closed and convex, we assume in the following that for all there exists with for all directions where for some t>0. This together with the Lipschitz condition on the Fréchet derivative of F guarantees that where L is the Lipschitz parameter. This means F has to be Fréchet-differentiable on the subset .

Moreover, we assume that we have noisy data with (2) and that for exact data y, a solution of (1.1) exists in .

Usually the problem of equation (1.1) is difficult due to its ill-posed property, and therefore, has to be regularized (see 1).

Tikhonov regularization is certainly the most well-known regularization technique 2. It's convergence in application to nonlinear ill-posed problem have been studied in 3–6. An alternative to use is iterative methods. Iterative methods like regularized Gauss–Newton method 7, steepest descent method 8, Landweber's method 9, and other modifications (see e.g. 10–14) are attractive for numerical solution of nonlinear ill-posed operator equations, since these methods can be implemented in a straightforward way.

Indeed, such iterative methods have good convergence properties under some restrictions, and therefore, they have been used widely to deal with inverse problems. However, all these methods are locally convergent; the convergence depends highly on good initial estimates. In most practical applications it is difficult to find good initial values. Therefore, other widely convergent (even global convergent) approaches are needed to find solutions to inverse problems.

The homotopy method is a powerful tool for solving nonlinear problems due to its widely convergent property 15. It is an interesting research problem to apply the homotopy method to solve inverse problems for differential equations. Keller and Perozzi's paper 16 may be the first work to use the homotopy method to solve the inverse problems. They combined a homotopy path-following formulism with the singularity theory to track multiple solutions of a geophysical inverse problem 17; Han et al. developed a widely convergent homotopy method for determining the distributed parameters of an elliptical equation 18; Everett transformed a 2–D discrete inverse problem of Helmholtz equation to a corresponding polynomial system and solved it by using the homotopy method and got all the roots of the system 19; Jegen applied the classic Euler–Newton numerical continuation scheme to inverse problems 20; Bao and Liu suggested a homotopy-regularization method for inverse scattering problems with multi-experimental limited aperture data 21; Han designed a homotopy method for the inversion of a two-dimensional acoustic wave equation 22.

In this article, we consider a new idea. Firstly, the homotopy method is introduced and combined with Tikhonov regularization to give a widely convergent method. Secondly, we can expand the parameter a(x) and F(a) in some finite element spaces, then the problem of estimating a(x) is reduced to solving a finite dimensional vector formed by the coefficients of the finite expansion and the constraints described by a closed and convex set are guaranteed by projection. We call this method homotopy-projection method. Finally, as a practical application, a parameter estimation problem of elliptical equation is solved. We describe the computational process in detail for this numerical example.

The remainder of the article is organized as follows. Section 2 deals with the principle of homotopy-projection method, and constructs a practical method. In section 3, a model of an elliptical equation is described and some numerical simulations are made. Finally, in section 4, some conclusions are given.

2. The homotopy-projection method

2.1. Homotopy-regularization method

Since the problem (1.1) is ill-posed, regularization method must be employed. In Tikhonov regularization, the problem (1.1) is replaced by the minimization problem (3) where α is the regularization parameter, a⁰ is an initial guess for a solution of (1.1).

The iteratively regularized Gauss–Newton method (see 7) (4) may be used to solve (2.1). To maintain stability, a growth restriction for some r>1 on the regularization parameters is imposed, which, e.g., allows for a geometrically decaying sequence for some t∈(0,1) and α₀ is a small constant. It is a locally convergent scheme, and will converge very fast when the initial guess a⁰ falls within the convergence domain. However it is usually very difficult to provide a good initial guess. Therefore, we consider to introduce the homotopy method.

2.1.1. Homotopy theory

We briefly introduce the principle of homotopy theory for solving nonlinear operator equations like (1.1). For more details we refer to the tutorial given by Watson 23. A homotopy function H(a,λ) is constructed by adding a scalar homotopy parameter λ∈[0,1] and a simple function G(a) to the “target function” F(a)−y, such that The “start system” of nonlinear equations G(a)=0 can be chosen arbitrarily, and at least has one known solution a⁰, which can be chosen as the initial guess for the whole computation. We wish that there may exists a curve a=a(λ), λ ∈[0,1], which satisfies the homotopy equation (5) Then it is obvious that a(0)=a⁰, and , which is a solution of the operator equation (1.1). Therefore, a(λ) is a curve, connected a⁰ with . If we use some numerical method to trace this curve from a known point a⁰, then we can finally reach the solution .

Basically, there are two ways to trace this curve. The first one is based on the assumption that H(a,λ) is differentiable with respect to a and λ. Differentiating each side of (2.3) on λ, we have (6) As a satisfies the initial condition a(0)=a⁰, the question to determine a(λ) is turned out to be an initial value problem of ordinary differential equation (2.4). By some numerical integration formulae, one can get an approximation of . The second one is to divide the interval [0,1] into , then use some iterative methods to solve the operator equation sequentially (7) Since the solution a^m−1 of the (m−1)th equation is obtained (note that the solution of the 0-th equation a⁰ is already known), a^m−1 can be used as the initial approximation of the m-th equation of (2.5). When λ_m−λ_m−1 is sufficiently small, a^m−1 would be expected as a good approximation to a^m, then by using a locally convergent iterative method we can achieve its convergent result. In this article, we use this method as our path tracing method.

Actually, there are other methods to trace the curve connected a⁰ with , when it can not be expressed as the function of λ. But it is out of our theme.

2.1.2. A homotopy method for inversion

Now, we consider the problem (1.1). If we know fairly a prior estimation a⁰ of , we can use the iteratively-Gauss–Newton method (2.2) to solve (1.1). However, this may be not the practical situation. Usually we can not provide a good estimation a⁰ for (1.1), and the Levenberg–Marquardt method may be used in trying for lots of initial estimation a⁰ to give a reasonable approximation of . This is a major problem when carrying out inversions.

In order to solve (2.1), we consider the fixed point homotopy equation (8) where λ ∈[0,1] is the homotopy parameter, α(λ) is the regularized parameter which continuously depends on λ (e.g., and this time, ), a⁰ is an arbitrary point. Obviously, when λ=0, ; when λ=1, it becomes . Therefore, H(a,λ) may be regarded as a homotopy map between and , and . Clearly, the minimizer of (2.6) satisfies (9)

We propose the minimizer a(λ) is a continuous function for λ∈ [0,1], which is the basic for the following arithmetic. In order to ensure this property, we have to incorporate some smoothness conditions as the majority of research did for nonlinear ill-posed problems. Throughout this article we will assume that the following conditions hold (see 25):

a.	F is twice Fréchet-differentiable with continuous second derivative.
b.	The first derivative is Lipschitz-continuous, (10)
c.	There exists ω∈ Y with (11)

Remark We do not intend to palliate the fact that source conditions (2.9) depending on the problem under consideration, might imposes severe restriction on the exact solution and it is difficult to verify. However, in the numerical experiments we can see that this condition is not necessarily satisfied.

In order to prove the continuous theorem, we need the following Lemma 2.1. The proof is similar to the proof of in 1. Here, for completeness, we still prove it.

LEMMA 2.1

Suppose the assumptions (a), (b), (c) are satisfied. Then (12) and (13) hold.

Proof

Since a(λ) is the minimizer of the functional H(a,λ), we obtain Therefore Set . From Taylor's Theorem, we know namely and Therefore, and thus (14) and the estimates (2.10) and (2.11) follow immediately by using (2.9). Lemma 2.1 is proved.▪

Now we prove the continuous dependence of a\,(λ) on λ.

THEOREM 1

Let the assumption of lemma 1 hold. And that a sequence {λ_m} with is given. If (15) holds, then and the error estimate (16) with (17) (18) yield.

Proof

For the following we set with Taylor's Theorem, we see Moreover, let us define then and Defining we know Since a^δ(λ) is a minimizer of the functional H(a,λ), therefore, (19) From (2.17), we know we get Since we know (20) Now by using the estimates (2.10) and (2.11), and setting then we have (21) and (22) By setting we get (23) (24) Inserting (2.19–2.22) in (2.18) yields By setting (25) we find Due to . With (2.13) we obtain we have It is obvious such that The continuity is proved.▪

Due to the continuity of the map λ→ a(λ), we can divide the interval [0, 1] into . For , we use some iterative method to solve (2.7) sequently. As the solution a⁰ of the 0-th equation of (2.7) is known, it can be used as the initial approximation of the next equation. Assume that the approximate solution a^δ,m of the m-th equation has already been found. For computing the solution a^δ,m+1 of the (m+1) th equation, we consider a successive linearization method. Suppose a^δ,m is known, for computing , we replace F(a) by the linear function , and substitute F(a) by in (2.7) to obtain (26) The solution of (2.24) can be regarded as the next approximation to a^δ,m+1: (27) From (2.25), the approximation a^M of the M-th equation can be solved, which can be taken as the initial estimate to the method (2.2). Iterate repeatedly by using (2.2) until the regularized approximation of is obtained. Therefore, (2.25) and (2.2) constitutes a stable and widely convergent method for the problem (1.1).

If we choose λ_m=m/M by an isometric division, m_T≡0, and α is constant. Then (2.25) becomes a more simple formula: (28)

2.2. Projected iterative methods

In this article, we consider the situation that closeness of some iterate a^δ,m to the exact solution is not sufficient for well-definedness of F(a^δ,m), or that we search for a solution satisfying additional constrains. In this situation we eventually have to proj ect our iterates into the domain of F in order to carry out the next step or, more generally, stay in the feasible set. For this purpose, we use the (possibly nonlinear) metric projector onto . Then the regularized Gauss–Newton methods (2.2) arrive at (29) with the regularizing operator The homotopy method (2.25) arrive at (30) with the regularizing operator Note that if lies within , then the projection can be omitted and the respective step is equivalent to (2.2) or (2.26).

Kaltenbacher and Neubauer had proved the feasibility and validity of this projection method in 26. Here we briefly introduce this theory.

In regularization theory, α>0 is a small regularization parameter, and the regularizing operator R_α satisfies (31) (32) (33) for some positive constants c₁, c₂, and c_s. Here the superscript † denotes the generalized inverse. With the assumption (34) and the uniformly bounded property of F^′, as long as the stopping index is chosen such that with a sufficiently small constant ζ, the iteration (2.27) is convergent (cf. [26, Theorem 4]). When we consider the iteration (2.28), the regularizing operator R_α turns to R_α(λ), whose parameter α(λ) continuously depends on λ. However, (2.29) is still satisfied under the condition λ→1 (namely α→ 0) and the fulfillment of (2.30) and (2.31) is obviously obtainable. As a result, with the corresponding assumption like (2.32), the iteration (2.28) is feasible.

When this projection method is applied to regularization methods, where the infinite-dimensional linear operator equation is projected to a finite-dimensional subspace of the data space , we assume that (35) and is solved in a best approximate sense, so that (36) where Q_m and P_m are the orthogonal projectors onto and , respectively. An advantage of regularization by discretization is that it enables the use of multi-grid method as optimal preconditions for the fast convergence of iterative solutions of the linear system in each Newton step.

Note that and that as m→∞. Hence, (2.29) and (2.31) hold. Moreover, it holds that (37)

Let us assume that the space have the property that (38) for all , where . Such properties are for instance fulfilled for finite element spaces and Sobolev spaces . The parameter h_m usually plays the role of a mesh size of the discretization, with h_m→ 0 as m→∞. If K has the smoothing property that (39) then we obtain an estimate (40) On the other hand, inverse inequalities yield an estimate for in terms of the mesh size, i.e., (41) for some and all linear operators K satisfying (42)

With the correspondence (43) for the regularization parameter, (2.35), (2.38), and (2.40) imply that (2.32) holds, where we additionally restrict the operators K to those satisfying (2.40). As a result, as long as (2.40) holds for all operators with . If the additional condition (44) holds, (2.39) and (2.41) imply that R_α defined by (2.34) satisfies (2.30).

As pointed out in 26, (2.36), (2.37), (2.39), (2.40), and (2.42) are natural conditions in the context of parameter identification in PDEs and discretization by finite elements of splines.

3. A parameter estimation problem of an elliptical equation

Let us consider the following parameter estimation problem of an elliptical equation, namely the problem of identifying the space dependent diffusivity a=a(x) in (45) from measurements of u in the domain . A solution to this problem exists if with a.e. and if . For this purpose, usually the domain of the forward operator is chosen as the set of functions in the Hilbert space with ϵ>0. Then one can not only verify Lipschitz continuity of the derivative (cf. (2.8) but also more restrictive assumptions on the nonlinearity of the forward operator F. We project onto the set for some constants . This means, we look for approximate solutions in L^∞ but consider their convergence to the exact solution in L².

This example has been described in 26, here for completeness we still enumerate some properties of the model.

We will now verify all assumptions on the forward operator F made in the previous section for the one-dimensional case Ω=[0,1]: one can show that F(a) is given by and that F is differentiable in the sense of the last section, namely for all and such that for some t>0. Obviously and is exist. If f∈ L¹[0,1], then F^′ satisfies (2.8): for it holds that The adjoint of F^′ is given by where u(a) is the solution of (3.1) and the dot denotes derivative with respect to s. The source condition (2.9) is equivalent to the conditions and ω is given by

To numerically test the approach proposed here, we applied it to the test problem: (46) Note that and a⁰ satisfy the source conditions with ω=99.9f.

The solution of the forward problem (3.1) was based on linear finite elements on a uniform grid with mesh size h=1/10. The same finite element space was used to approximate a, i.e., where u_n solves the linear equation The Fréchet-derivative is given by where du_n solves the linear equation u_n is as above, and A_n(h) is similarly defined as A_n(a). The diffusivity is approximated by

(2.27) in this setting then reads as follows: (47) and (2.28) arrives at (48)

In order to test the feasibility and to study the general characteristics of the new method, we carry out the numerical simulation procedure for two cases. In the process of computation, we take as error level.

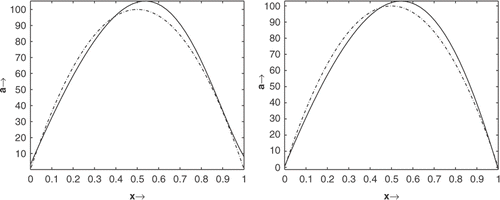
At first we take a⁰=100 for exact data (δ=0) with . Both iterations (2.27), (2.28) and (2.2) are convergent (figure 1). Without projection, we do not get convergence via the regularized Gauss–Newton method (2.2), while the homotopy method still provides good results.

Figure 1. a₀=100. The numerical results for the iterations (2.25) (left) and (2.28) and (2.2) (right) without noise. Note: Solid line denotes numerical results a^m and dashed line denotes exact solution a*.

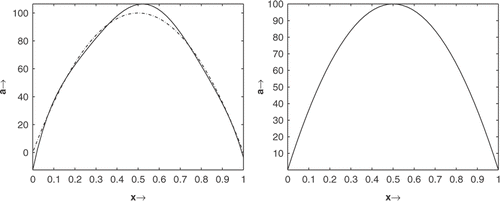
Then, with , we choose a⁰=0.01 so that the source condition is no longer satisfied. The numerical results show that only iteration (2.28) and (2.2) can converge and 5% noise level can be added (figure 2). The numerical results show that our method is indeed a widely convergent method and can improve stability of classical methods.

Figure 2. a₀=0.01. The numerical results for the iterations (2.28) and (2.2) without noise (left) and 5% noise added (right). Note: Solid line denotes numerical results a^m and dashed line denotes exact solution a*.

4. Conclusions

For the general parameter estimation problems, we have designed the homotopy-projection method. First, we introduce the homotopy method to overcome the defects of local convergence of conventional iterative methods. Secondly, the discretization by finite elements is not only to make the problem of estimating a function a(x) reduce solving a n-dimensional vector a_n but also a_n does not take part in the discretization. This two properties will reduce the cost of computation. Finally, constrains defined by closed and convex sets can be handled by projection. As a practical application, the method has been used successfully to solve the parameter estimation problems of an elliptical equation. It turns out to be stable and widely convergent. We have done other numerical experiments on an inverse problem of wave equation, and on auto-convolution equation, they all show our method's effectiveness (cf. 22).

Acknowledgement

This work is supported by the National Science Foundation of China under grant No.40544016, and the Multidiscipline Scientific Research Foundation of Harbin Institute of Technology under No. HIT. MD 2003.19.