Determination of the leading coefficient in fourth-order Sturm–Liouville operator from boundary measurements

Abstract

An inverse coefficient identification problems associated with the fourth-order Sturm–Liouville equation in the steady state Euler–Bernoulli beam theory is investigated. Unlike previous studies in which spectral data are used as additional information, in this article only boundary information is used, hence nondestructive tests can be employed in practical applications.

Keywords:

• Sturm–Liouville equation
• Beam theory
• Inverse problems

1. Introduction

The determination of the leading coefficient in fourth-order ODEs has been formulated as a classical Sturm–Liouville problem in 1,2. The central idea in both these articles is the reconstruction of the flexural rigidity coefficient k(x) (i.e., the product of the modulus of elasticity E and the moment of inertia I: k = EI) in the ODE (k(x)u''(x))''=λ u(x)/k(x) from the spectral data λ, where u(x) is the deflection of the beam. Other inverse spectral data reconstructions of k(x) have been investigated in 3–8. However, spectral data is not available in many physical problems. In the case of steady-state vibrations of a beam on an elastic foundation, where the governing equation is the steady-state Euler–Bernoulli beam equation (1) where f (x) is the transverse distributed load to which the beam is subjected and q(x) is the foundation modulus, one can also attempt to determine k(x) when q(x) ≡ 0 from the full knowledge of u(x) and f (x), 9. See also 10,11 for extensions to higher dimensions. However, this data, although it guarantees the uniqueness of the solution, implies that unlimited measurements of the deflection u(x) along the beam have to be performed, which again may not be practically feasible in some applications. Therefore, the aim of this article is to study what can be retrieved about k(x), when the additional data is extremely limited and is confined to boundary measurements only; hence nondestructive material testing techniques may be employed in practice. More concretely, we consider the following inverse coefficient problem (ICP).

2. Inverse coefficient problem (ICP)

We study, finding the flexural rigidity k(x) of a beam [a,b] from the class of admissible functions (2) where are some prescribed constants, and the deflection u(x) from the class of functions (clamped essential conditions at the end x = a of the beam) (3) such that equation (1) is satisfied in the equivalent system form (4) subject to the natural boundary conditions on the bending moment M(x) and the shear force M'(x) at the end x = b of the beam, namely, (5) and the additional measured data: (6) (7) (8) (9) An analogous inverse problem for second-order Sturm–Liouville operator has been investigated in 12–17.

Assume that and q(x) ≥ 0 for x ∈ [a,b]. Then the direct problem (DP) given by equations (3–5), when k ∈ Kis given, has a unique solution . This solution is understood in the weak sense, i.e., (10) Alternatively, instead of solving the variational problem (10), since B is a bilinear and symmetric form and l is linear we can minimize over the total energy of the beam .

From (6–9), the ICP consists in solving the nonlinear equations (11) with respect to k ∈ K. In practice however, the measured values for α_b, β_b, γ_a, and δ_a are not exact and, consequently, it is preferable to find a quasi-solution of the ICP as the solution of the following minimization problem: Find k ∈ K₀ such that , where K₀ ⊂ K is a compact set of admissible coefficients and (12) The existence of a quasi-solution of the ICP has been established elsewhere 18.

Recovering the unknown function k=k(x) ∈ K by using only four boundary measurements evidently is a nonunique solution problem and therefore, in the next section, we will restrict our consideration to a particular class of approximants for k.

3. Finite-dimensional approximation

The numerical algorithm for solving the ICP can be based on the minimization of the function (12) over the solution of the DP. This means that one needs to solve a finite number of DPs and therefore, the accuracy of the ICP depends also on the accuracy of the numerical algorithm that one would choose for solving the DP. Since the approach presented is based on the weak solution theory, for the numerical solution of the DP we will develop a variational finite-difference scheme, 19.

Introduce the uniform mesh where h=(b-a)/N>0 is the mesh step and denote by for . Integrating equation (4) on , we obtain (13) where φ (x) = M'(x) and . We approximate , where and , and denoting , equation (13) recasts as (14) Integrating φ (x)=M'(x) on and on we obtain (15) where . Introducing (15) into (14), we obtain (16) Integrating equation (4) on , we obtain (17) where , and . Integrating on and on we obtain (18) Introducing (18) into (17), we obtain (19) From u(a)=0 and (5) we have (20) Integrating equation (4) on and using (5), we obtain (21) We approximate , where and , and denoting , equation (21) recasts as (22) Integrating φ (x)=M'(x) on , we obtain (23) Thus from (22) and (23), we obtain (24) Integrating equation (4) on and using that u'(a)=0, we obtain, (25) where . Integrating ψ (x)=u'(x) on , we obtain (26) Thus (27) Integrating equation (4) on and using (9), we obtain (28) Approximating , and denoting , equation (28) recasts as (29) Integrating φ (x)=M'(x) on and using (8), we obtain (30) Thus from (29) and (30), we obtain (31) Integrating equation (4) on and using (7), we obtain (32) where . Integrating ψ (x)=u'(x) on and using (6), we obtain (33) Thus from (32) and (33), we obtain (34) To summarize (16), (19), (20), (24), and (27), we have obtained the following system of equations (35) On the uniform mesh W_h, the finite-difference scheme has the second-order accuracy O (h²) in the norm C(W_h), 19. The system (35) contains (2N+2) equations with (2N+2) unknowns u_i and M_i for , which can be solved for the DP using the Gaussian elimination method or a standard factorization solver. Once these values have been evaluated accurately for a sufficiently large N, the values of α_b, β_b, γ_a, and δ_a can be obtained from (6), (8), (31), and (34), namely (36) To describe a finite-dimensional analogue of the ICP we need to interpolate the function k(x), to approximate the DP and to parameterize the functional I(k), as well. Since there are only four measured data, it is reasonable to interpolate the function μ (x)=1/k(x) by the cubic Lagrange's polynomials (37) where ξ ₀=a, , , and ξ ₃=b. In this case, the ICP can be reformulated as a parameterized inverse problem of recovering the quadruplet , , from the measured data (6–9).

Based on the approximation (37), equation (36) gives a nonlinear system of four equations with four unknowns which is solved as a constrained minimization problem with simple positivity bounds on the variables using the NAG routine E04UCF. Here instead of (12) we minimize the objective function (38) subject to .

4. Numerical results and discussion

For simplicity we take [a,b]=[0,1].

The initial guess to start the iterative nonlinear constrained minimization procedure has been taken as μ _i=0.5, . Other initial guesses produced the same results confirming the robustness of the method employed.

The constraint has been numerically imposed as .

The gradient of the function (38) has been numerically calculated using a forward finite-difference method with a step of 10^-5 such that any further decrease in this value did not affect the numerical results significantly; in addition the NAG routine E04UCF employed indicates whether the directional derivative of the objective function and the finite-difference approximation are in closed agreement.

Note that even for exact data there exists a numerical noise resulted from the discrepancy between the exact values and the numerical values obtained by solving the DP with a uniform mesh size h=1/N.

Example 4.1

In this benchmark test example, we choose the deflection function (39) We also take q(x)=k(x)=1 and . Then α ₁=e-2, β ₁=e-1, γ ₀=1, γ ₁=e, δ ₀=1, δ ₁=e.

In the ICP, we seek the function μ (x)=1 in the set (37) given by (40) i.e., we seek to retrieve μ _i=1, . We also contaminate the input data (6–9) with ε percentage of noise as , , , . Since the ICP is ill-posed, the iterations were stopped according to the discrepancy principle 20.

First, in order to investigate the convergence of the numerical solution as h=1/N decreases to zero, and hence conclude the uniqueness of the ICP given by Example 4.1, we consider the case ε = 0. Table 1 shows the retrieved values of for various values of N ∈ {20, 40, 80 }. From this table it can be seen that as N increases, the objective function (38) also decreases and the numerical solution converges to the exact solution μ_i=1, .

Table 1. The numerical values of obtained for various values of N ∈ {20, 40, 80 }, when ε = 0. The stopping iteration numbers k and the values of the objective function (38) are also included.

N	μ0	μ1	μ2	μ3	k	Obj f
20	0.88	1.04	0.97	1.05	23	2.6 × 10^-7
40	0.90	1.03	0.97	1.08	25	3.7 × 10^-8
80	0.97	1.00	0.99	1.04	41	7.5 × 10^-9

Next, in order to investigate the stability of the numerical solution with respect to noise in the input data (6–9), we fix N = 40 and vary the amount of noise ε. Table 2 shows the retrieved values of for various values of ε.

Table 2. The numerical values of obtained for various values of ε ∈ {± 0.1, ± 0.05, 0 }, when N = 40. The stopping iteration numbers k and the values of the objective function (38) are also included.

ε	μ0	μ1	μ2	μ3	k	Obj f
−0.1	0.69	1.11	0.73	0.53	2	3.0 × 10^-2
−0.05	0.70	1.15	0.76	0.54	2	7.5 × 10^-3
0	0.90	1.03	0.97	1.08	25	3.7 × 10^-8
0.05	0.70	1.22	0.95	0.56	5	7.4 × 10^-3
0.1	0.73	1.26	0.86	0.55	2	3.0 × 10^-2

In the next figures 1 and 2, we fix N = 40.

Figure 1. The numerical solution for (a) the deflection u(x), and (b) the flexural rigidity k(x), for various values of ε = {±0.1, ±0.05, 0}, in comparison with the exact solution (u(x),k(x))=(e^x-1-x,x) for example 4.1.

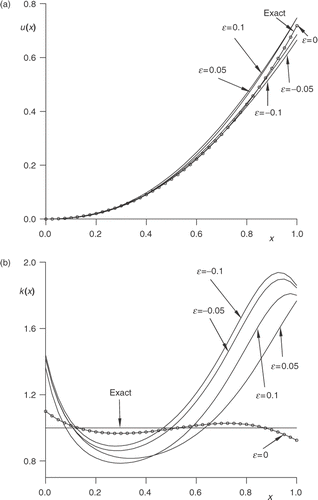
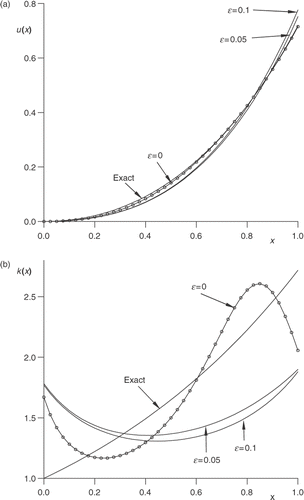
Figure 2. The numerical solution for (a) the deflection u(x), and (b) the flexural rigidity k(x), for various values of ε = {±0.1, ±0.05, 0}, in comparison with the exact solution (u(x),k(x))=(e^x-1-x,1) for example 4.2.

Figure 1(a) and (b) show the numerical solutions for u and k, respectively, in comparison with the exact solution (u(x),k(x))=(e^x-1-x,1). From these figures it can be seen that reasonable accurate and stable solutions are obtained, especially for the deflection in figure 1(a), which are consistent with the amount of noise ε included in the input data.

Finally, it is reported that when compared with the numerical results of figure 2(a) and (b) from 18, the results of figure 1(a) and (b) of the present article are more accurate.

Example 4.2

We consider the same deflection function as that given by equation (39), but now we take a spacewise dependent reciprocal flexural rigidity μ (x)=1/k(x)= which does not belong to the set of Lagrange's polynomials (37). Further taking q(x)=1 equation (1) gives f(x)=4e^2x+ e^x-x-1. Also, equations (6–9) perturbed by noise give , , , and . We also have γ ₁=e² and δ ₁=2e².

From (40) and the Maclaurin expansion of the function e^−x we expect, μ ₀ ≈ 1, μ ₁ ≈ 58/81,μ ₂=41/81, and μ ₃=1/3, and these values have been used to calculate an estimate of the noise added in the input data which is required to be known in advance for the discrepancy principle to be applicable.

Figure 2(a) and (b) show the numerical solutions for u and k, respectively, in comparison with the exact solution (u(x),k(x))=(e^x-1-x,e^x). From these figures it can be seen that reasonably good and stable numerical approximations of the exact solution are obtained, especially for the deflection in figure 2(a), although . This latter fact is reflected in a quite poor estimation of the flexural rigidity in figure 2b.

Since the ICP under investigation is nonlinear, error estimates seem difficult to obtain at this stage and they are deferred to a future work.

5. Conclusions

In this article, the determination of the flexural rigidity and the deflection of a beam in the Euler–Bernoulli beam theory has been investigated. Since only limited boundary measurements are considered as available, a particular class of Lagrange's polynomials in which the flexural rigidity is sought has been proposed. Since the inverse problem is well-posed for the deflection solution, but it is ill-posed for the flexural rigidity, the nonlinear least-squares functional which naturally minimizes the gap between the calculated and the noisy measured input data has been regularized by stopping the iterations at the first iteration for which the discrepancy principle is satisfied. The numerical method based on a nonlinear constrained minimization procedure with simple positivity bounds on the variables produced stable and reasonably accurate numerical approximate solutions. Error analysis for the numerical approximation is deferred to a future work.

Acknowledgement

The first author would like to thank the UK Royal Society for some financial support received for performing this research.