Padé approximations for identification of air bubble volume from temperature- or frequency-dependent permittivity of a two-component mixture

Abstract

The article presents a numerical method developed for identification of information about structural parameters of a two-component mixture from effective complex permittivity measurements. The identification is based on the reconstruction of the spectral function in the analytic Stieltjes representation of the effective permittivity using Padé approximation. The spectral function contains all information about the microgeometry of the mixture, it is used to calculate volume fractions of the components in the mixture. Padé approximation is derived from a constrained minimization problem. Numerical results of recovering volume fraction of air in mixtures of air prolate and oblate spheroidal inclusions in water and in ethanol show good agreement of theoretical and predicted values. The proposed method can be used for estimating volume fractions and other structural parameters using the effective complex permittivity of two-component composite materials.

Keywords:

• Spectral representation
• Effective complex permittivity
• Two-component composite
• Ellipsoidal inclusion
• Padé approximations

Mathematics Subject Classifications::

• 41A20
• 45Q05
• 78A48

1. Introduction

Many engineering problems deal with materials which are finely structured heterogeneous mixtures and ask for volume fractions of different components. We consider a mixture of air bubbles and liquid as an example of such two-component composite medium. Evaluation of volume of air bubbles is a problem of identification of microstructural information (the volume fractions of materials) in the composite. The problem of estimating the fractions of the constituents in the composite from measured effective complex permittivity was introduced in 1, 2. The explicit formulas for the bounds on the volume fraction of one material were derived in 3 for isotropic composites and in 4 for anisotropic mixtures. The approach is based on analytic representation of the effective permittivity ε* of a mixture of two materials with permittivity ε₁ and ε₂ as a Stieltjes function. This analytic integral representation was developed in homogenization theory for computing bounds for the effective permittivity of an arbitrary two-component mixture in 5–12. The information about the microgeometry of the mixture is contained in the spectral measure in this analytic representation. The identification of the measure from measured effective properties is called inverse homogenization. The problem has a unique solution if measurements of effective permittivity ε* are available in an interval of frequencies 13. Various inversion algorithms for recovering the spectral measure and spectral density function of a two-phase composite from the measured data have been proposed 13–17.

Our approach is based on reconstruction of the spectral measure in the analytic integral representation of the effective complex permittivity ε* using rational function (Padé) approximations 18. It is assumed that the effective complex permittivity of the mixture can be measured in an interval of frequencies. The reconstruction problem is ill-posed and requires regularization. We consider Tikhonov regularization method 19 with constraints described below. When the spectral function is recovered, the volume fraction of inclusions is calculated as the first moment of the reconstructed function. We use the developed technique in numerical simulations and show results of reconstruction of the spectral function and estimation of the air bubbles volume from the effective complex permittivity for mixtures with ellipsoidal inclusions of air bubbles in water and air bubbles in ethanol. To demonstrate accuracy of computation of the spectral function, we compare numerically found parameters with parameters of the spectral functions derived analytically for the models of composites with prolate and oblate spheroidal inclusions. The computed values of the effective permittivity, poles and amplitudes of the spectral functions, and air volume fraction are in good agreement with true values. The method is applicable to identification of the volume of components in other two-phase composite materials with arbitrary microgeometry.

2. Motivation

Determination of the volume of one material in a mixture, such as air volume in a sample liquid, is an important problem in many fields 20–24. Recently, a nuclei size measurement technique was developed in 22, based on a dispersion relation for propagation of sound waves through a bubbly liquid. The experimental measurements of the phase velocity and attenuation for monochromatic acoustic waves in bubbly liquids were used to recover the bubble population density function. In 24, a design and application of a prototype optical tomography for imaging and monitoring shapes of gas bubbles moving in a liquid was explored; an experimental and computational result on bubble formation in microfluidic devices was reported briefly in 25.

Dealing with complex permittivity measurements, the straightforward approach to evaluation of the volume fractions of different materials in the composite would be a model-based approach. Several dielectric models with specific assumptions have been proposed to describe the permittivity of mixtures using given permittivity constants and volume fractions of the constituents 26–28. The well-known Maxwell Garnett (MG) model 29 uses the mean field approximation for the effective permittivity of random composites. In the MG model, the inclusions of spherical particles are assumed to be randomly distributed in the mixture. The effective permittivity ε* = ε*(f,ε_i,ε_b) is determined by the volume fraction f of the first component, permittivity ε_i of inclusions, and permittivity ε_b of background, (1) Therefore, assuming this model, the volume fraction f = f(ε*,ε_i,ε_b) of inclusions can be estimated given measured value of the effective complex permittivity ε* and values of permittivity of the components ε_i, ε_b: (2) However, air bubbles are often not of a spherical shape (see photographs in 22 or 24), as well as often for real composite materials, no geometrical information about the shape and size distribution of inclusions is known. We calculated estimates for the volume fraction of one component using inverse formula (2) from the values of the effective complex permittivity ε* corresponding to mixtures with different microgeometries. The values of the estimates are shown in table 1; they are not accurate. To obtain these estimates we calculated the effective permittivity of a mixture of water and air inclusions of elliptical or cylindrical shape at the frequency ω = 9 GHz and used formula (2) to find the air volume. In the first column, f_os and f_ps represent the estimates of air volume fractions from the complex permittivity measurements for the mixtures with randomly oriented inclusions of oblate spheroids shape (OS) and inclusions of prolate spheroids shape (PS); f_cc for the mixture with coated circular-cylinder inclusions, measured in x direction; and f_xcc and f_zcc for the mixture with confocal coated elliptical-cylinder inclusions, measured in x and z direction, respectively. The summarized results in table 1, show a large discrepancy between the true volume fractions and values estimated using inverse MG formula (2). This demonstrates the necessity to develop a method which would not be based on a particular model of the geometric structure. The present article discusses an approach that avoids specific assumptions about the microgeometry of the mixture and works efficiently for any two-component composite material.

Table 1. Inaccuracy of estimates of volume fraction using inverse Maxwell Garnett formula (2) for composites with different microgeometries

f	2%	5%	8%	12%	18%	22%	28%	35%
fos	3.87%	9.39%	14.63%	21.18%	30.19%	35.72%	43.38%	51.48%
fps	2.18%	5.45%	8.69%	12.99%	19.37%	23.59%	29.85%	37.08%
fcc	2.63%	6.52%	10.33%	15.30%	22.53%	27.21%	34.01%	41.64%
fxcc	3.02%	7.43%	11.71%	17.22%	25.09%	30.09%	37.24%	45.10%
fzcc	1.35%	3.41%	5.51%	8.38%	12.83%	15.91%	20.69%	26.54%

3. Analytic representation for effective complex permittivity

We consider three-dimensional composite medium which is formed of two homogeneous, isotropic phases with permittivity ε_i and ε_b. It is assumed that the wavelength of applied electromagnetic fields is much larger than the scale of inhomogeneities of the microstructure. In the quasi-static approximation, the effective permittivity ε* is defined as (3) where E₀ is the applied electric field along the z-direction, D and E are the displacement and electric field, and V is the volume of the medium.

With introduced parameter s which contains the values of the permittivity of the components, the function F(s) = 1 −ε*/ε_b has analytic representation: (4) The function F(s) is analytic outside the [0, 1)-interval in the complex s-plane and all its singularities are in the unit interval 5–12. We approximate the function μ by a step function with a finite number of steps, so that (5) Then, the approximation of the function F(s) has a finite number of simple poles, with all the poles being located in the unit interval s∈[0, 1) and with real residues between 0 and 1: (6) Here s_n is the n-th simple pole with residue A_n, q is the total number of poles.

It was shown in 8 that the volume fraction f of subdomains occupied by the first material is a sum of all residues in this representation (sum rule): (7) Notice that the effective permittivity of a composite material could be frequency-dependent; it follows then from (4) and (6) that (8) Equation (8) gives an approximation of the frequency-dependent complex permittivity function ε*(ω)/ε_b(ω). The real parameters A_n and s_n in this representation depend purely on the microgeometry of the composite.

Let us assume that the effective permittivity ε*(ω) of a composite medium can be measured in a range of frequencies or temperatures. We describe a method which will allow us to identify parameters A_n and s_n and to construct approximation (8). The unknown parameter of micro-structural geometry, volume fraction f, can then be calculated using (7).

4. Padé approximation of the spectral function

The idea of the method is to use constrained partial fraction decomposition of the Padé approximation of the function F(s) calculated from the measured values of the effective complex permittivity ε*. The constraints for the poles and residues of the partial fractions are given in (6). We use a least squares approximation of F(s) by a rational function to construct Padé approximation.

The Padé approximation of F(s) is defined as 30 (9) where a_i and b_j are the polynomial coefficients of two polynomials a(s) and b(s) of orders p and q, respectively. The orders p and q of the polynomials in the numerator and denominator are chosen arbitrary or could be obtained taking into account the topology of composite material.

We assume that the function F(s) has at least one pole, and normalize the polynomial coefficient b₁ = 1 in the denominator b(s). All the poles s_j (j = 1, 2, …, q) of denominator b(s) in (9) are simple, and the following partial fraction decomposition holds: (10) If the function F(s) is obtained from measured data pairs , k = 1, 2, …, N, where N is the total number of the complex measured values of F(s), then (9) can be written as (11) where a_i (i = 0, …, p), b_j (j = 0, …, q, j ≠ 1) are required unknown coefficients. Equation (11) can be rewritten as (12) Therefore, the unknown coefficients a_i (i = 0, …, p), b_j (j = 0, …, q, j ≠ 1) of the ratio a(s)/b(s) are determined by solving the following linear system of equations (13) Where (14) (15) and the symbol [·]* indicates complex conjugate transposed matrix. It should be noted that in order to uniquely determine the coefficients a_i (i = 0, …, p), b_j (j = 0, …, q, j ≠ 1), the total number of the measurements must be greater or equal to the number of coefficients, i.e., N > p + q + 1. The reconstruction problem in (13) is ill-posed and requires regularization to develop a stable numerical algorithm. In this study we use constrained minimization method with constraints described below.

To derive solution to the problem (13), we use complex matrices S = S_r + iS_i and d = d_r + id_i where subindices r and i indicate the real and imaginary parts of the matrices. To find the vector of Padé coefficients c we formulate the least squares minimization problem: (16) Here denotes the usual Euclidean norm. The solution of the minimization problem is ill-posed. A widely used approach to regularize the problem is to introduce a penalization term and rewrite the minimization problem (16) as follows 19 (17) Here λ is a regularization parameter. The choice of the regularization parameter λ has an important role in solving the regularized problem, since in the dual minimization problem, λ is the Lagrange multiplier by the constraint for the norm of the solution. However, the problem (17) is still ill-posed due to the data noise present in the elements of the matrix S as well as in the right-hand side vector d. This leads to the problem in which both the coefficient matrix and the right-hand side vector are not precisely known. The total least squares method could be used for solution of this kind of linear least squares problems 31, 32. Application of this method will be discussed elsewhere. In the current article, we use inequalities (6) for the residues and poles of the function F(s) to impose constraints for the set of minimizers of the problem. The regularized solution c for the problem (13) is obtained as a solution of the following constrained least squares minimization problem (18) Here parameters A_i and s_i are residues and poles of the partial fractions decomposition (10) of the reconstructed Padé approximation of the spectral function. The corresponding Euler equation is (19) After reconstruction of the coefficients a_i (i = 0, …, p), b_j (j = 0, …, q, j ≠ 1) of Padé approximation and decomposition of the approximation into partial fractions (10), the volume fraction of the first component in the mixture is calculated using formula (7).

5. Spectral representation for mixtures with ellipsoidal inclusions

As a test example we consider a microgeometry formed by ellipsoidal inclusions of volume fraction f with a dielectric permittivity ε_i immersed in a much larger homogeneous background with a dielectric constant ε_b. The effective permittivity for a three-dimensional isotropic two-component mixture with randomly oriented ellipsoidal inclusions with semi-axes a_x, a_y, and a_z 28 is (20) where N_x, N_y, and N_z are depolarization factors of the three orthogonal directions, respectively, satisfying N_x + N_y + N_z = 1. The depolarization factor N_x in the x-direction is given as (21) The other two depolarization factors, N_y and N_z, are obtained by interchanging a_y and a_x, and a_z and a_x in the above integral.

The MG formula (1) predicts the effective permittivity of the mixture with inclusions of spherical shape (S); this is the special case of (20) when depolarization factors are equal: N_x = N_y = N_z = 1/3. We consider two other models of composites with special shape of inclusions: mixtures with randomly oriented PS and with randomly oriented OS. For the prolate spheroids (a_x > a_y = a_z), (21) gives (22) where e is the eccentricity, . For oblate spheroids (a_x = a_y > a_z), (23) where .

Let s = 1/(1 − ε_i/ε_b). The function F(s) corresponding to the effective permittivity defined by the MG formula (1) can be written as (24) In the complex s-plane, this gives a pole at the location s = (1 − f )/3 for the spectral function corresponding to F_MG(s). The residue is the volume fraction f of the inclusion material.

Using the introduced parameter s, the functions F_PS(s) and F_OS(s) corresponding to mixtures with randomly oriented prolate-spheroidally shaped inclusions (22) and with randomly oriented oblate-spheroidally shaped inclusions (23) can also be brought to the simple fractions form. For a mixture with randomly oriented PS-shaped inclusions (22) and with randomly oriented OS-shaped inclusions (23), the expression has the same two-term form (25) where the parameters s₁, s₂ are the following: (26) and A₁, A₂ for the PS model are given as (27) For a mixture with OS inclusions, the parameters A₁, A₂ are (28) It is easy to check that the sum rule (7) for the residues in (24) and (25) is satisfied.

6. Numerical examples

In this section we present results of recovery of volume fraction of air from numerically simulated effective permittivity of different mixtures. We consider mixtures of air bubbles in water and in ethanol, assuming various microgeometries and simulating measurements in various ranges of frequencies and temperatures.

The permittivity of air considered as inclusion material in the mixture, is a dispersionless constant (ε_i = 1). The frequencies-dependent permittivity of the background material (water) is given by the first-order Debye relaxation model: (29) Here ε_s is the static dielectric constant (the value at zero frequency), ε_∞ is the value at high frequency, τ is the relaxation time, and ω = 2π f₀ is the angular frequency, with f₀ being the frequency of the field. The parameters ε_s, ε_∞ and τ are functions of temperature for liquid water, they satisfy 26 (30) where T is the temperature in kelvins.

6.1. A mixture of air bubbles in water: frequency-dependent data

In the first example, the measurements of the effective complex permittivity for a mixture of air bubbles and water were simulated using described models of microstructure of composite materials. The parameters of the dielectric properties of liquid water taken as the background matrix material in the mixture (ε_b = ε_water(ω)) at the temperature of +20°C have the values: (31) The values of the effective permittivity ε* for the mixture of air and water with air inclusions of spherical and ellipsoidal shape were calculated using the MG formula (1) and formulas (20) for composites with PS and OS inclusions. The Padé coefficients of the rational function a(s)/b(s) were reconstructed using the developed algorithm from the simulated values of the effective complex permittivity. Then these coefficients were used to compute a partial fraction decomposition of a(s)/b(s). Approximation to the function F(s) and the spectral function μ is obtained from the partial fraction representation.

The first set of numerical experiments uses 15 data points in a range of frequencies from ω = 0.001 GHz to 100 GHz. The computed air volume fractions, as well as residues and poles in the spectral representation, are summarized in table 2 for the mixture with PS inclusions and in table 3 for the OS inclusion model. Figure 1 shows results of reconstruction of the Padé coefficients (a) and the spectral function μ (b) for the case of 15% volume of air. Real and imaginary parts of the complex permittivity ε* used as data, are shown in figure 2.

Figure 1. Reconstruction of Padé coefficients (a) and of the spectral measure μ (b) for air–bubble–water mixtures with spherical and ellipsoidal inclusions (air volume fraction f = 15%).

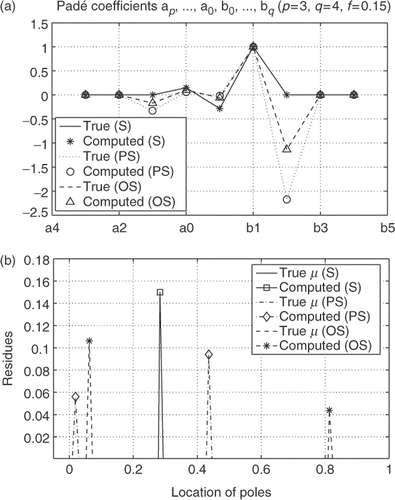
Figure 2. True and computed effective permittivity, real ε* (a) and imaginary ε* (b), for mixtures of air bubbles and water for various types of inclusions (ω = 0.001–100 GHz, f = 15%).

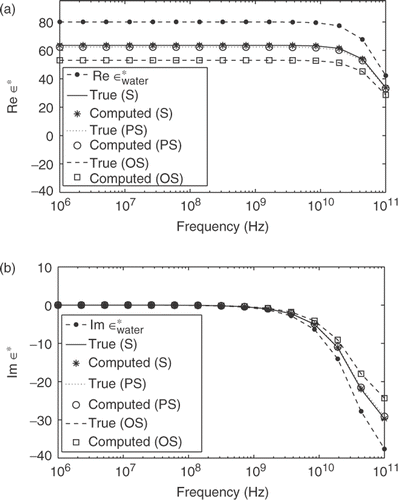
Table 2. Computed air volume fractions, residues, and poles for mixtures of air PS inclusions and water (p = 3, q = 4, ω = 0.001–100 GHz, N = 15, a_x = 1.0, a_y = a_z = 0.1)

	f ^(1)
True	0.1500000000	0.0939393210	0.0560606710	0.4409891718	0.0191537683
Computed	0.1500083310	0.0939455453	0.0560627857	0.4409842627	0.0190235381
	f ^(2)
True	0.2000000000	0.1221298493	0.0778701507	0.4247604408	0.0187158327
Computed	0.2000059640	0.1221353167	0.0778706473	0.4247570959	0.0186441566

Table 3. Computed air volume fractions, residues, and poles for mixtures of OS inclusions of air in water (p = 3, q = 4, ω = 0.001–100 GHz, N = 15, a_x = a_y = 1.0, a_z = 0.1)

	F^(1)
True	0.1500000000	0.0438721121	0.1061278879	0.8181605442	0.0622415940
Computed	0.1500008302	0.0438721152	0.1061287150	0.8181605416	0.0622386215
	F ^(2)
True	0.2000000000	0.0556227876	0.1443772124	0.8041332749	0.0596021967
Computed	0.1999992461	0.0556227838	0.1443764623	0.8041332774	0.0596042135

The next set of numerical experiments uses model of composite with spherical inclusions. The complex permittivity ε* and spectral function F(s) used as data (26 data points in a range of frequencies between 10⁸ Hz and 10¹⁵ Hz), are shown in figure 3. Another set of data has 15 data points in a range of frequencies from 0.1 GHz to 10 GHz for the same structural model. The imaginary parts of the complex permittivity ε* used as data, corresponding to air volume fraction f = 6, 12, 18, 25%, are shown in figure 4(a). The reconstructed spectral functions μ (b) for the case of air volume fraction f = 6, 12, 18, 25% are shown in figure 4(b). The true delta function solutions which for different volume fractions, have poles at the locations s = 0.3133, 0.2933, 0.2733, 0.2499, with residues corresponding to volume fractions f = 0.06, 0.12, 0.18, 0.25, are reconstructed practically exactly in the case when there is no noise in the data.

Figure 3. True and computed ε* (a) and F(s) (b) for mixtures of air bubbles in water with frequency as parameter (f = 6, 12, 18, 25%).

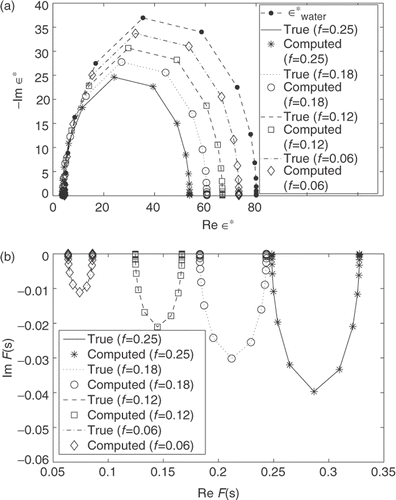
Figure 4. (a): True and computed imaginary part of ε*. (b): Reconstruction of poles and residues of the spectral measure μ for mixtures of air bubbles in water (f = 6, 12, 18, 25%).

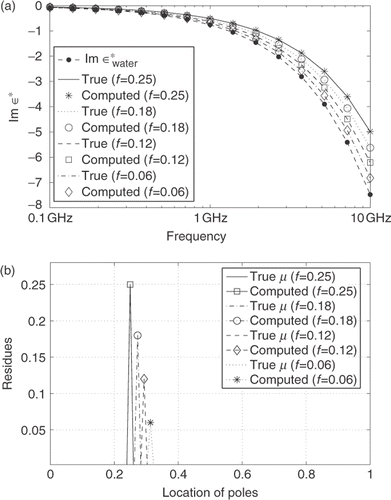
These numerical examples show that in the complex plane, the function F(s) and spectral function μ depend strongly on the volume fraction of the air bubble phase.

6.2. Temperature-dependent mixture of air bubbles in water

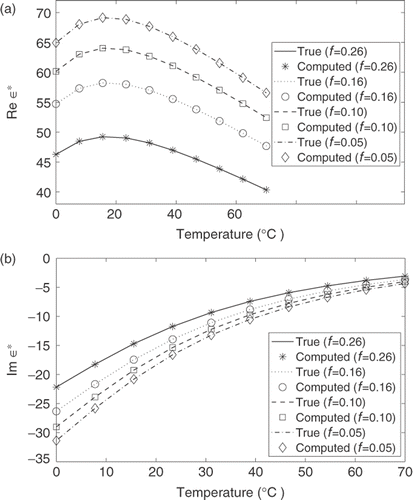
Consider a mixture of air bubbles and water and assume that the measurements of the effective permittivity are done at the same frequency in some range of temperatures. The parameters of temperature dependence of the dielectric properties of water are the same as in (30). We consider the fixed frequency ω = 9 GHz and temperature changing in two ranges between 16°C and 24°C, and 0°C and 70°C. We use composites containing spherical and ellipsoidal air inclusions to model the microgeometry of the mixture in order to simulate the measured data.

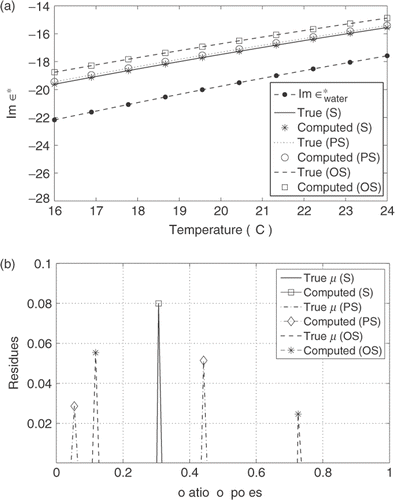
Applying the described algorithm, we reconstruct the spectral function μ using simulated values of the effective complex permittivity. The computed air volume fractions, as well as residues and poles in the spectral representation for the mixtures with spheroidal inclusions, are shown in tables 4 and 5. These results are calculated from the data in the temperature range t = 16–24°C for the air volume fractions f = 8% and f = 22%. Table 4 contains values for the mixtures with PS inclusions. The true and computed values for the OS inclusion model are shown in table 5.

Table 4. Computed air volume fractions, residues, and poles for mixtures of water with air PS inclusions for temperature-dependent model (p = 2, q = 3, ω = 9 GHz, t = 16–24°C, N = 12, a_x = 1.0, a_y = a_z = 0.2)

	f ^(1)
True	0.0800000000	0.0514152860	0.0285847140	0.4470068534	0.0542369649
Computed	0.0800073471	0.0514347208	0.0285726263	0.4469757731	0.0537757169
	f ^(2)
True	0.2200000000	0.1304021521	0.0895978479	0.4036551002	0.0509220514
Computed	0.2200034171	0.1304168819	0.0895865352	0.4036458682	0.0508385162

Table 5. Computed air volume fractions, residues, and poles for mixtures of air bubbles and water for OS inclusions model for temperature-dependent permittivity (p = 2, q = 3, ω = 9 GHz, t = 16–24°C, N = 12, a_x = a_y = 1.0, a_z = 0.2)

	f^(1)
True	0.0800000000	0.0246448180	0.0553551820	0.7306883841	0.1178869054
Computed	0.0800034519	0.0246452484	0.0553582035	0.7306873834	0.1178416913
	f^(2)
True	0.2200000000	0.0576535126	0.1623464874	0.6971532549	0.1047553680
Computed	0.2200003376	0.0576535759	0.1623467617	0.6971531862	0.1047537157

Figure 5 shows reconstruction results for mixtures of water with air ellipsoidal inclusions using data in the temperature range t = 16–24°C for air volume fraction f = 8%. The results of reconstruction of the spectral function μ are shown in figure 5 (b). Figure 5 (a) shows the imaginary part of the simulated complex permittivity ε* used as data in this series of computations.

Figure 5. Reconstruction results for mixtures of air bubbles and water for spherical and ellipsoidal shape of air inclusions using data in the temperature range t = 16–24°C for air volume fraction f = 8%. (a): true and computed imaginary part of the effective permittivity ε*. (b): reconstruction of the spectral function μ. The frequency of the applied field is ω = 9 GHz.

Figure 6 shows results of reconstruction of Padé coefficients (a), residues and poles of the spectral measure μ (b) from the effective permittivity calculated for the model of composites with spherical shape of inclusions for data corresponding to temperature changing from t = 0°C to t = 70°C. The true delta function solution has a pole at the location s = 0.3167 with residue (volume fraction) f = 0.05; s = 0.3 with residue f = 0.1; s = 0.28 with residue f = 0.16; s = 0.2467 with residue f = 0.26. These parameters of the spectral function are reconstructed almost exactly. Figure 7 shows real and imaginary parts of the complex permittivity ε* used as data. It was found that in the case when there is no noise in the data, even for a small number of measured data used in calculation, the reconstruction algorithm still works almost perfectly. The difference between the true and reconstructed spectral functions cannot be distinguished on the graphs.

Figure 6. Reconstruction of Padé coefficients (a) and residues and poles of the spectral function μ (b) for mixtures of air bubbles in water (f = 5, 10, 16, 26%).

Figure 7. True and computed real ε* (a) and imaginary ε* (b) for mixtures of air bubbles in water for temperature ranging from 0°C to 70°C (ω = 9 GHz, f = 5, 10, 16, 26%).

6.3. Frequency-dependent mixture of air bubbles in ethanol

Consider a frequency-dependent mixture of air bubbles and ethanol using a model of composite with air inclusions, ε_i = 1, in ethanol considered as background, ε_b = ε_ethanol. The complex permittivity of ethanol in the mixture is given by the Debye relaxation function in (29) with the parameters of liquid ethanol at the temperature of +20°C having the values 26: (32)

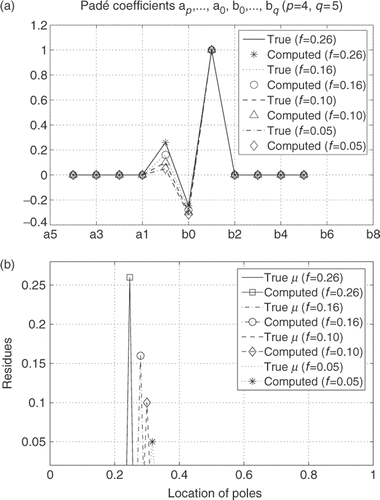
Simulated values of the effective complex permittivity in a range of frequencies between 0.0001 and 10 GHz at 18 discrete points of frequencies were used to reconstruct the Padé coefficients and to recover the function μ from the partial fraction decomposition of the obtained rational function. The computed values for the parameters of the spectral function and air volume fractions are presented in table 6 for the mixture containing PS inclusions and in table 7 for the model of composite with OS inclusions. Figure 8 shows the results of reconstruction for the case of 25% volume of air. Figure 8 (left) shows the effective permittivity ε* and the reconstructed density of the spectral function μ is presented on the right.

Figure 8. Results for air–bubble–ethanol mixtures modeled as composites with spherical or ellipsoidal inclusions; air volume fraction is f = 25%. (a): imaginary part of F(s). (b): reconstructed density of the spectral function μ.

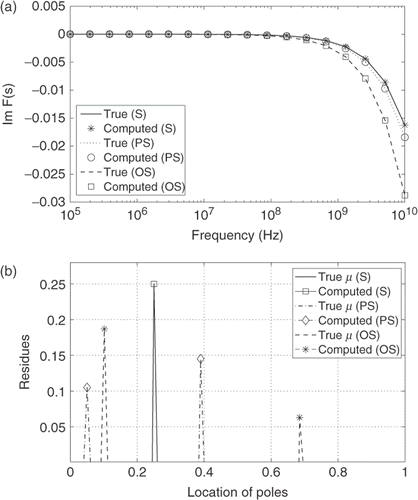
Table 6. Mixture of air bubbles and ethanol for model with PS inclusions. Computed air volume fractions, residues and poles of the spectral function (p = 4, q = 5, ω = 0.0001–10 GHz, N = 18, a_x = 1.0, a_y = a_x = 0.2)

	f ^(1)
True	0.1600000000	0.0984847250	0.0615152750	0.4221392527	0.0524378989
Computed	0.1599923817	0.0984801848	0.0615121968	0.4221423234	0.0525178879
	f ^(2)
True	0.2500000000	0.1451174222	0.1048825778	0.3944740572	0.0501030944
Computed	0.2500003328	0.1451177010	0.1048826317	0.3944739293	0.0501008288

Table 7. Computed air volume fractions, residues and poles for mixtures of ethanol and air OS inclusions (p = 4, q = 5, ω = 0.0001–10 GHz, N = 18, a_x = a_y = 1.0, a_z = 0.2)

	f^(1)
True	0.1600000000	0.0451243848	0.1148756152	0.7113459992	0.1105626237
Computed	0.1599988656	0.0451243686	0.1148744970	0.7113460161	0.1105657771
	f ^(2)
True	0.2500000000	0.0629883927	0.1870116073	0.6901619560	0.1017466668
Computed	0.2499987958	0.0629883695	0.1870104263	0.6901619742	0.1017488013

Figure 9 shows results of reconstruction of the Padé coefficients (a), residues and poles of the spectral function μ (b) from simulated effective permittivity in the range of frequency (ω = 10⁷–10¹³ Hz). The geometric model is a model of composites with spherical inclusions. The true solution is a delta function with a pole whose location depends on the air volume fraction. For the volume fractions f = 0.04, 0.08, 0.14, 0.28, the position of the pole is s = 0.32, s = 0.3067, s = 0.2867, s = 0.24. Residues and position of the poles is reconstructed very accurately, with no difference between the theoretical and reconstructed functions seen in the figure. Figure 10 shows the real and imaginary parts of the complex permittivity ε* used in calculations.

Figure 9. Reconstruction of Padé coefficients (a), residues and poles of spectral measure μ (b) for mixtures of air bubbles in ethanol with volume fractions f = 4, 8, 14, 28%.

Figure 10. True and computed real ε* (a) and imaginary ε* (b) for mixtures of air bubbles in ethanol (volume fractions f = 4, 8, 14, 28%).

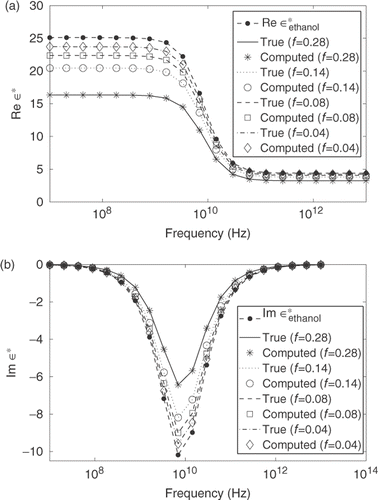
The imaginary part of ε* has its minimum at the relaxation frequency f_r = 1/(2πτ) as shown in figure 10(b). Though we use a small number of the data points in this example, the reconstruction algorithm works very accurately.

6.4. Sensitivity analysis of the method

We numerically examined the sensitivity of the algorithm to the noise added to the input data. We used a uniformly distributed random noise calculated as percentage of the true value at each measured point. A summary of the sensitivity analysis for the mixture of air bubbles in water is shown in table 8. The effective permittivity for these numerical experiments was calculated using MG mixing formula. Figure 11(a) shows the reconstruction of residues and poles of spectral measure μ for the mixture of air bubbles and water with spherical inclusion of air component (frequency as parameter, volume fraction f = 18%) for different noise levels added to the input data.

Figure 11. Figure (a) shows reconstruction of residues and poles of the spectral function μ for the mixture of air bubbles in water (true volume fraction f = 18%) with noise added to the input data. Figure (b) shows the volume fraction estimated using inverse MG formula (2) and computed with the presented method. The data are simulated using composites with different microgeometries. Stars * denote the volume fraction computed using the developed method.

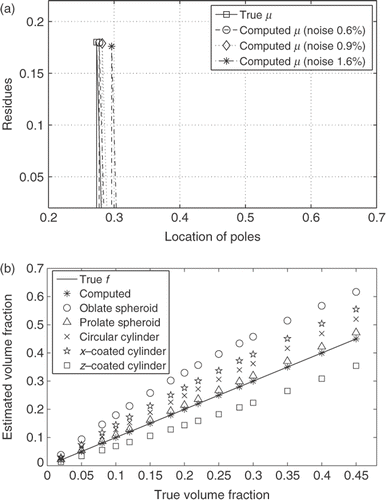
Table 8. Calculated values of volume fraction and pole location for air and water mixture using data with added noise (ω = 10⁸–10¹⁵ Hz, f = 0.18)

Noise	True volume f = 0.1800	True pole s = 0.2733
0.06%	0.1796	0.2772
0.09%	0.1788	0.2818
1.60%	0.1756	0.2992

6.5. Comparison with inverse Maxwell Garnett formula for composites of different microgeometries

To verify the approach, we compare results of computation of volume fraction using presented method with the estimates obtained from inverse MG formula (2). The data for the frequency-dependent effective permittivity for a mixture of air bubbles and water were simulated using various models of composites with spheroidal inclusions and models of different cylindrical microgeometries. The effective permittivity of a composite formed by confocal coated elliptical cylinders can be calculated as the tensor 12 where (33) (34) (35) with c_j and e_j (j = 1, 2) representing the semi-axis lengths of the core and exterior surface of the coated elliptical cylinders. We use numerically simulated data of , , and to estimate the volume fraction of air component in the mixture of air bubbles and water. For the microgeometry of coated circular cylinders, the parameters used in calculation of the complex permittivity measurements or in (33) and (34), are c₁/c₂ = e₁/e₂ = 1. For the microgeometry of confocal coated elliptical cylinders, the permittivity , , and was calculated using values c₁/c₂ = e₁/e₂ = 5/6. We used formulas (20) to compute effective permittivity of composites with PS and OS inclusions. The frequency was assumed to be ω = 9 GHz.

Figure 11(b) shows the calculated volume fraction f of air bubble component in the composite versus the true volume fraction using the developed method and applying the inverse MG formula (2). The results are shown for various volume fractions and for various ellipsoidal and cylindrical microgeometries. While the inverse MG estimates give large discrepancy between the true and calculated values, especially for large volume fractions, the results computed using the presented spectral function method, always agree precisely with the true values.

7. Conclusions

The spectral representation of the effective complex permittivity of composite materials separates the geometric information and dependence on material properties. The spectral function can be found from measurements of effective complex permittivity and then can be used to calculate volume fraction of one component in the mixture.

The numerical method based on the rational approximations has been developed for reconstruction of the spectral function μ for mixtures of two-component materials. The method was tested using analytical models of composites with spherical and ellipsoidal inclusions. The method was used to evaluate the volume fraction of air in mixtures of air bubbles and water and of air bubbles and ethanol. Comparison with the true volume fraction and with estimates obtained using inverse MG formula, demonstrates the effectiveness of the presented approach.

Acknowledgement

This work was supported by NSF grants DMS-0508901 and DMS-0411035.