Magnetoencephalography source localization using improved simplex method

Abstract

Nelder–Mead downhill simplex method, a kind of deterministic optimization algorithms, has been used extensively for magnetoencephalography (MEG) dipolar source localization problems because it does not require any functional differentiation. Like many other deterministic algorithms, however, it can be easily trapped in local optima when being applied to complex inverse problems with multiple simultaneous sources. In the present study, some modifications have been made to improve its capability of finding global optima. Those include (1) constructing an initial simplex based upon sensitivity of variables and (2) introducing a shaking technique based on polynomial interpolation. The efficiency of the proposed method was tested using analytical test functions and simulated MEG data. The simulation results demonstrate that the improved downhill simplex method can result in more reliable inverse solutions than the conventional one.

Keywords:

• Nelder–Mead downhill simplex method
• Magnetoencephalography source localization
• Deterministic optimization algorithm
• Bioelectromagnetic inverse problem

1. Introduction

Magnetoencephalography (MEG) is a kind of non-invasive imaging modalities to explore dynamic neuronal activities of human brain 1. MEG measures magnetic field induced from neural current flows inside the head using very sensitive magnetic field sensors like superconducting quantum interference device (SQUID). Nowadays, it is widely used to study cognitive and sensory processes of normal brain as well as treating serious neurological disorders such as epilepsy, Parkinson's disease, and so on.

To estimate the neural current sources from external magnetic field measurements, one should solve an inverse problem that has been referred to as a neuromgnetic inverse problem (NIP). To solve the inverse problem and estimate the human brain activity more efficiently, many approaches have been studied 2. Among them, two types of models are generally used: equivalent current dipole (ECD) model and distributed source model. The former assumes small numbers of ECDs to approximate the flow of electrical current in small brain areas. The parameters of the dipoles are then determined by solving an optimization problem to minimize the Frobenius norm between measured and calculated magnetic fields 34. On the other hand, the latter assumes a lot of ECDs scattered in predetermined source space and orientations and/or strengths of the dipoles are then determined using linear or nonlinear estimation methods 56. Each model has its own pros and cons. The distributed source model is better for estimating multiple simultaneous brain activations with large spatial extent, but it often results in too widespread source estimates or unwanted spurious sources 7.

On the contrary, the ECD model is more proper to localize small numbers of focal brain activations, which usually occurs in sensory or clinical applications. Studies by de Munck et al. 8 showed that an ECD provides an excellent fit to the observed data for certain classes of distributed primary sources such as disks and annuli. Since it is simple to implement, easy to identify activated locations free of spurious sources and relatively robust to various internal and external noises, it has been proved to be a powerful exploration tool for many clinical studies 910.

In the MEG dipolar source localization, sufficient recording data, which guarantee a unique solution are not generally available and signals recorded by MEG are apt to be corrupted by various disturbances and noises. Since the acquired data contain limited information and the shape of the objective function is very complex, the objective function has many locally optimal solutions. Therefore, it is of importance to pick up proper optimization algorithms that can find a globally optimal solution in a more efficient manner. Generally, there are two kinds of optimization algorithms: stochastic algorithms and deterministic algorithms. Stochastic algorithms, such as genetic algorithm (GA) and simulated annealing, can prevent solutions from trapping in local optima, because they utilize concepts of probability to search better solutions. When using any kinds of stochastic algorithms, however, severe computational burden is inevitable. Moreover, the stochastic-type algorithms are not adequate to optimize large numbers of parameters. On the other hand, deterministic algorithms are very fast throughout the whole process and robust if good initial starting points are assumed, because they use gradient information in order to determine search direction. Therefore, deterministic algorithms have been widely used for NIP. Among the deterministic algorithms, in this article, Nelder–Mead downhill simplex method is adopted 11 since it does not require any functional derivatives and it is much faster than any other stochastic algorithms.

Generally, single dipoles can be localized robustly with the conventional method. When data from whole cortex during a complex task are analyzed, however, several interacting sources are seen and they need to be modeled via multiple dipoles. Then, like other deterministic optimization algorithms, the solutions of the downhill simplex method are easily trapped in local optima or even diverge, unless reasonably accurate initial locations are given 11.

In the present study, we made some modifications to the conventional Nelder–Mead downhill simplex method to tackle the above problem: (1) constructing an initial simplex using sensitivity of variables and (2) adopting a shaking technique based on polynomial interpolation. From simulation studies using test functions and artificial MEG data, it is demonstrated that the improved downhill simplex method can result in more accurate and reliable dipole source estimates than the conventional one.

2. MEG source localization

As aforementioned, the main aim of MEG source localization is to find brain electrical activities using magnetic field measurements outside the head. To solve such NIP, forward solutions should be repeatedly solved at each iteration step. In the present study, we have used a homogeneous spherical volume conductor model to calculate magnetic field generated by few numbers of ECDs 9.

2.1. Forward problem

The physics of MEG can be described by the quasi-static approximation of Maxwell equations, because the useful frequency spectrum for electrophysiological signals in MEG is typically below 1 kHz. The current density at a point r produced by neuronal activity is divided into two components: a primary current flow J^p(r) related to the original neuronal electrical activity and a secondary current flow J^v(r) that results from the macroscopic electric field on charge carriers in the conducting medium. Hence, the current density J(r) can be written as (1) where σ(r) is the conductivity profile of the head tissues, which we will assume, for simplicity, to be isotropic.

An equivalent current dipole Q, approximating a localized primary current, is a widely used concept. Since the spatial resolutions of MEG are restricted due to the limited spatial arrangements of sensors, it is quite reasonable to assume a current dipole as an equivalent source for the unidirectional primary current that may extend over several square centimeters of cortex. The equivalent current dipole Q at r_Q can be thought of as a concentration of J^p(r) to a single point: (2) where δ(r) is the Dirac delta function.

The simplest approach to calculate magnetic fields outside the head is to assume the head as a single sphere. This rough assumption is useful for many clinical and research applications, especially when heavy iterative processes are required. In the homogeneous single sphere, the magnetic field at computing point r induced by a current dipole Q at r_Q can be expressed as (3) where with a = (r − r_Q), , and 12.

2.2. Inverse problem

The ECD model first assumes small numbers of dipolar sources to approximate the flow of electrical current in small brain areas. Each dipole has six independent parameters, which are components of dipole location vector (x, y, z) and dipole moment vector (Q_x, Q_y, Q_z). The parameters of the dipoles are then determined by using various kinds of optimization algorithms. Objective function, sometimes referred to as an error function, is defined as a norm of difference between measured and calculated magnetic fields. The error function that should be minimized can be expressed using the following Frobenius norm: (4) where x is the measured magnetic field signals, A is a lead field matrix that relates sensor positions and source locations, p represents location parameters of dipoles, and s is a corresponding dipole moment vector.

Assuming that there exists N dipoles and k time points, there will be 3N location parameters and 3Nk moment parameters, for an overall of 3N(k + 1) parameters. In practice, it is a very difficult optimization problem due to its large dimension. For example, if there are N = 3 dipoles and the time points k = 80, then we have to search for a 729-dimension parameter space to find the global optimum for this problem. If this is a linear problem, the size of the problem is acceptable; while for a nonlinear problem, its computational complexity will be overwhelming. Fortunately, the computational complexity of the problem can be greatly reduced by separating the linear and nonlinear parameters because x is a linear function of parameter s. The method to factor out the linear moments has been used by many researchers, and has been mathematically justified in 1314.

First, for any location parameter x, the optimal s that will minimize E is determined as (5) where A* is Moore–Penrose pseudo-inverse, which can be found by A* = VW⁺U^T, where A = UWV^T is the singular value decomposition (SVD) and W⁺ is the inverse of W 15.

When s is replaced with this pseudo-inverse solution before solving for p, the error function of the inverse problem becomes (6) where I is the square identity matrix. Now, we can see that the error function no longer depends on matrix s. The number of parameters of the error function has been reduced to 3N, for example, nine in case of three dipoles.

3. Simplex method

3.1. Conventional simplex algorithm – Nelder–Mead downhill simplex search

Downhill simplex method is a multidimensional unconstrained optimization method that was introduced by Nelder and Mead in 1965 16 and has been applied to many areas of economics, engineering and medicine. One of the reasons why the downhill simplex method has been so widely used is that the downhill simplex method does not require any differentiation of the error function. A ‘simplex’ means a geometrical figure, which is consisting of (n + 1) points in n-dimensions. For instances, a simplex is a triangle in 2-dimensions and it becomes a tetrahedron in 3-dimensions.

The conventional process of constructing an initial simplex is as follows: If we randomly choose a starting point as x₀, the other n points x_i are generated according to the relationship x_i = x₀ + λe_i (i = 1, …, n), where the e_i are unit orthogonal vectors and λ is a constant, which is typically equal to one 17–19.

When an initial simplex in 3-dimensions is assumed as figure 1(a), we select x_h and x_l, which represent a point with the highest functional value and that with the lowest functional value, respectively. In the minimization problem, the point x_h should be replaced with a better point. The ingredients of replacement process consist of four basic operations: reflection, expansion, contraction, and multi-contraction as shown in figures 1(b)–(d).

Figure 1. Available moves in the simplex method, in the case of three variables: (a) initial simplex, (b) reflection, (c) expansion, (d) contraction, and (e) multi-contraction.

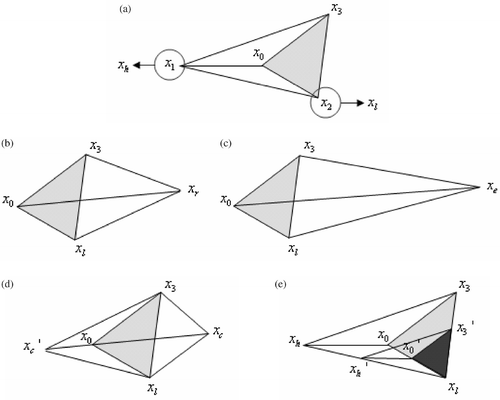
At the beginning of the replacement processes, x_h moves through a center of gravity of the other points and a reflected point x_r is generated (figure 1(b)). If x_r is better than all other points, the point expands in the same direction and an expanded point x_e is generated (figure 1(c)). The contraction step is performed when x_h is better than the reflected point. Contracted points x_c or x_c′ are tested if they are better than the original point x_h (figure 1(d)). If x_h is still better than the contracted points, a multi-contraction is performed (figure 1(e)). For the multi-contraction (or shrink), all points of the simplex are replaced with (x_l + x_i)/2.

Through these operations, the simplex can improve itself and come closer and closer to an optimum point sequentially. The process is terminated when the volume of the simplex becomes smaller than a predetermined value.

3.2. Improvement of simplex method 1–construction of a simplex

As stated above, the conventional downhill simplex method usually generates an initial simplex using the relationship x_i = x₀ + λe_i (i = 1, …, n), where the basis vector e_i has a unit magnitude. The efficiency of the downhill simplex method is highly dependent upon the initialization of the simplex since it determines initial moving patterns of the simplex. In practice, sensitivity of each variable, which is defined as ΔE/Δx, at a starting point is different from each other. Therefore, moving distance of a more sensitive point should be smaller than those of less sensitive points. This idea could be simply implemented by constructing an initial simplex considering the sensitivity difference of each vertex.

We calculated the sensitivity of each variable and the magnitude of each basis was then assigned inversely proportionally to the sensitivity value. If we assume the initial starting point as x₀, we generated the other points x_i according to the following relationship: (7) where s_i are sensitivities of each variable (s_i = ΔE/Δx_i), and λ is a constant of which the value is identical to that in the conventional initialization method. It can be seen from (7) that if a point has the higher sensitivity value, the distance from the initial starting point x₀ becomes the shorter, resulting in smaller displacement during reflection and contraction processes.

3.3. Improvement of simplex method 2–a shaking technique

The most crucial disadvantage of the conventional simplex method is that it is readily trapped in a local optimum when the error function has multiple local minima. To help a solution from trapping in a local optimum or freezing too early, we applied a ‘shaking technique’. The basic idea of the shaking technique is such that the simplex increases in volume when the simplex is converging to a certain point too early, e.g. within a predetermined number of iteration. In the present simulation studies, we applied the shaking technique at every multi-contraction step, which implies that better solutions cannot be found by basic operations such as reflection, extension, and contraction, when the current number of iteration does not exceed 60% of the predetermined number of iteration.

To determine the extension range, polynomial fit was used. First, we placed three more points along the direction of extension of a vertex P–the center of gravity of the other points P_c, a reflected point P_r, of which the distance from P_c was set to be 10 times farther than the distance between P_c and P, and a back-reflected point P_b, of which the distance from P was set to be 10 times farther than the distance between P_c and P. We then found a fourth-order polynomial function, which satisfies the functional values at P, P_c, P_r, and P_b. We then found a minimum of the polynomial function. If the minimum lies between P_r and P_b, P was replaced with the minimum point. If there is no minimum within the range, P was replaced with the nearest boundary vertex (P_r or P_b). A schematic example of the proposed shaking scheme is shown in figure 2.

Figure 2. The process of shaking, in the case of three variables.

4. Simulations and results

The efficiency of the improved downhill simplex method was extensively tested using analytical test functions and simulated MEG data.

4.1. Mathematical functions

The performance of the proposed method was investigated by applying it to the maximization of three mathematical functions, which have different complexity levels. The functions used are as follows: (8) where each function was defined as the summation of the bell-shaped functions and the number of peaks of func1, func2 and func3 was one, two, and three, respectively. All three functions have their global optimum at (10, 10).

We first examined the effect of simplex initialization upon the capability of the downhill simplex method. The following three different initialization methods were tested to the three analytic functions in (8): (Case 1) identical bases; (Case 2) bases proportional to the sensitivity of the variable; (Case 3) bases inversely proportional to the sensitivity. For each function, 500 repeated optimizations starting with different starting points were executed and the number of success was counted, where success implies that the difference between exact global optimum and estimated optimum was less than 1. Figure 3 shows the number of success with respect to the three different initialization methods.

Figure 3. The number of success according to types of functions.

In case of func1, an optimal value could be found accurately regardless of initialization methods. As the test function became complex, however, the number of success was decreased. The accuracy of (Case 3) is improved compared to that of (Case 1) and (Case 2), in case of func2 and func3. It means that (Case 3) can construct initial simplex, which is much closer to the optimal vertex and reflects properties of the objective function.

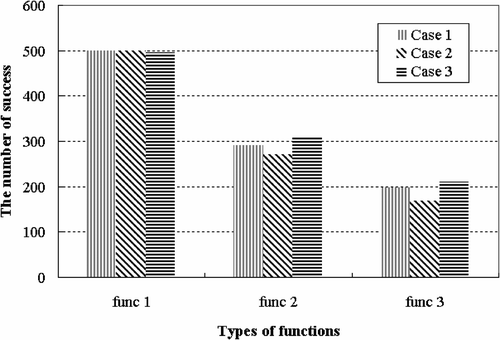
Next, we investigate the results of three shaking techniques: (Case 1) without shaking technique; (Case 2) enlarging size of the simplex to arbitrary size; (Case 3) increasing the simplex in volume by using polynomial fit. Figure 4(a) shows the number of success and figure 4(b) shows the number of iterations for the three cases, respectively.

Figure 4. (a) The number of success and (b) the number of iterations according to types of functions.

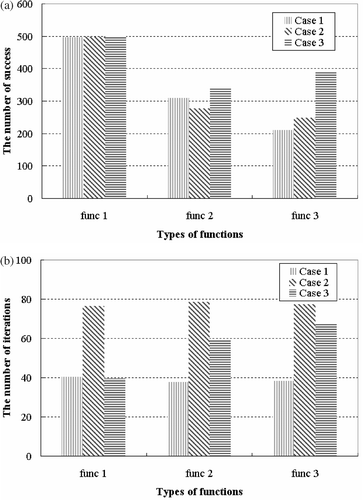
From these results, it can be known that the performance of (Case 3) is better than that of other methods as a test function becomes more complicated. Especially, in case of func3, the number of success of (Case 3) is nearly double to that of (Case 1). On the other hand, increment of computational burden was unavoidable when shaking techniques were used. In case of (Case 2), the number of iteration is always larger than those of the other methods. However, in case of (Case 3), the increasing rate of computational cost was proportional to the complexity of a function.

These results show that the shaking technique using polynomial fit has best performance and increment of computational burden is also reasonable.

4.2. MEG simulated data

The verification of the neuromagnetic inverse solution is very difficult compared to other inverse problems because there is no ways to know exact positions of neural activations in a real human brain. Therefore, in the present study, we applied our method to artificially constructed forward data sets assuming one and two simultaneous brain activations.

4.2.1. Simulation for a single activation

For the calculation of forward data, we assume a dipole source at an arbitrary position. The source intensity pattern I was defined as follows: (9) where the value of h was determined by means of a trial and error process in order to make the calculated magnetic field similar to the measurement data. After the forward calculation of magnetic field assuming 600 Hz-sampling rate, we added white Gaussian noise to each sensor. The noise is scaled in order for signal-to-noise ratio to be approximately 10 dB. A 148-channel MEG magnetometer system was assumed.

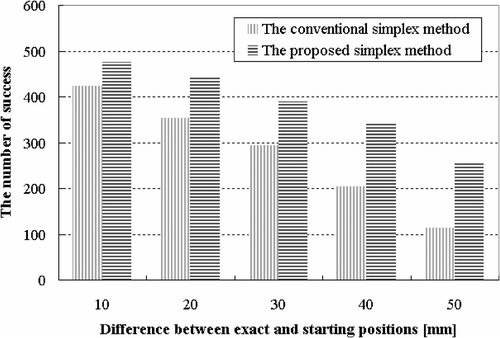
In case of deterministic algorithms such as the simplex method, estimation of a starting position has great influence on accuracy and computational cost. To investigate the effect of starting position, therefore, the inverse problem was repeatedly solved for 500 simulations with different locations in proportion to the increase of distance between the exact source position and the starting position. The distances ranged from 10 mm to 50 mm with interval of 10 mm. Table 1 shows average of localization errors and the number of iterations with respect to the distance from the exact solution to the starting point. The localization error is defined as the distance between the exact and estimated source positions, which is as follows: (10) In case of the single activation, both of conventional and proposed simplex methods could yield good results, of which the average localization error of 500 simulations was within 5 mm. However, the performance of the proposed method is superior to that of conventional one when the difference between the exact and starting position is large. It demonstrates that the proposed method is less sensitive to the starting points.

Table 1. Average of localization error and the number of iterations with respect to the distance from the exact and initial points

	The conventional simplex method		The proposed simplex method
	Error [mm]	The number of iteration	Error [mm]	The number of iteration
10 [mm]	1.94 (0.72)	129	1.92 (0.74)	349
20 [mm]	1.98 (0.78)	144	1.96 (0.77)	351
30 [mm]	1.99 (0.79)	152	2.00 (0.77)	356
40 [mm]	2.22 (3.24)	154	2.01 (0.78)	351
50 [mm]	3.03 (7.29)	164	2.10 (2.57)	356
The values in parentheses are SDs.

4.2.2. Extended simulation for multiple activations

The proposed approach was applied to more complex data simulated with two simultaneous activations. After calculating the magnetic field, we also added white Gaussian noise (SNR = 10 dB). First, 500 simulations with different locations were performed. Then, the number of success was counted, where success implies that the localization error is less than 10 [mm]. Figure 5 shows the number of success for conventional and proposed simplex method, respectively. As stated before, it is verified that a solution of the conventional simplex algorithm is easily trapped in local optima or even diverges. Such possible phantom solutions due to the incomplete convergence of the optimization process could be dangerous for a patient. From the results, however, we can see that such risk can be considerably reduced by using the proposed technique. Moreover, since the MEG results are usually used with other brain mapping modalities such as functional MRI to diagnose brain diseases, such risky situation seldom occurs in clinical applications.

Figure 5. The number of success according to difference between exact and starting positions.

Table 2 shows the average of localization error and the number of iterations obtained from the successful results. Inspite of the simulation conditions were different from the previous ones, we could see that the proposed technique resulted in the most reliable source estimate.

Table 2. Average of localization error and the number of iterations with respect to the distance from the exact and initial points

	The conventional simplex method		The proposed simplex method
	Error [mm]	The number of iteration	Error [mm]	The number of iteration
10 [mm]	6.07 (3.29)	319	5.95 (3.09)	431
20 [mm]	6.13 (2.97)	336	5.92 (2.85)	435
30 [mm]	6.37 (3.31)	351	5.81 (2.91)	434
40 [mm]	6.72 (3.56)	363	5.92 (3.10)	436
50 [mm]	7.48 (3.29)	362	6.06 (2.98)	440

5. Conclusions

In this article, an improved simplex method was proposed. The proposed method includes constructing an initial simplex using sensitivity of variables and performing a shaking technique using polynomial fit. To verify the performance of the method, some simulation studies such as mathematical test functions and MEG source localization were performed. From the results, we could demonstrate that the improved simplex method is a great utility in achieving reliable optimization of multivariate systems.