Identification of an internal material boundary

Abstract

The goal of this article is to provide a simple and fast numerical method to estimate an internal shape of a material by exploiting certain measurements performed on its external boundary. This inverse problem is formulated as a least-squares minimization problem. A numerical approach to this minimization problem based on the domain derivation ideas is outlined. Real implementation is achieved with the Freefem software. Numerical tests are provided to demonstrate the efficiency of the proposed method. Special attention is given to the impact of the material thermophysical properties on the quality of the identification. The effect of the errors in the measurements on the identification is also investigated.

Keywords:

• Output least-squares method
• Inverse heat conduction problem
• Domain derivation
• Finite element method

AMS Subject Classifications::

• 80A20
• 80A23
• 65K10

1. Introduction

Techniques of inverse problems have been, widely, applied in estimating parameters of thermal processes such thermal conductivity, specific heat capacity, boundaries conditions 1–4. These techniques have also been used in estimating some inaccessible part of the boundary of a domain being moving 5–7 or fix 8–10. Thermal imaging, which is a technique based on these inverse methods, is employed in detecting eventual defects or cracks within a manufactured material. It consists in applying a known heat flux on the accessible boundary and measuring the temperature response. Then, by inverse resolution, identify internal shape or parameters. Several studies devoted to problems of shape identification using steady heat equation, have been reported in literature 8,9,11–13. Also other inverse geometric problems using steady thermographic techniques, known as infrared computerized axial tomography IR-CAT, have been considered in 14–16.

The mathematical development of the domain-derivative techniques allows the construction of efficient numerical algorithm able to recover the shape of a domain from some measurements, performed on accessible boundaries 17–19. The unsteady heat equation is considered in these works. In this context, we propose to identify an internal boundary of a material from the knowledge of the heat flux and the temperature on the external one. We assume that the internal boundary is in contact with a medium at uniform temperature. This boundary is kept under a constant temperature condition.

The outline of this article is as follows. In section 2, we first begin by setting the equations governing the heat transfer in the material and then we set the physical problem. In section 3, we parameterize the unknown boundary by approximating its radial function using trigonometric polynomials and terminate by formulating the corresponding mathematical optimization problem. The derivation of the temperature with respect to the boundary is obtained through the solution of an initial boundary-value problem presented in section 4. Section 5 is devoted to space and time discretizations, numerical algorithm and the used FreeFem subroutines. In the last section, we present a variety of numerical tests of the proposed method carried out with simulated measurements.

2. Posing of the physical problem

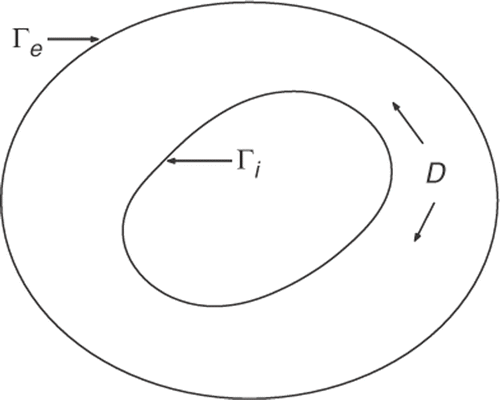
The considered material occupies the bounded domain D ⊂ ℝ² with smooth boundary Γ = Γ_i ∪ Γ_e, as shown in figure 1.

Figure 1. Domain D description.

The temperature evolution in the material is described by the following system: (1) where ρ, c and λ are the density, the specific heat capacity and the thermal conductivity of the material, respectively. These parameters are assumed to be constant, which is justifiable if temperature variations are sufficiently small. Q represents the energy, per unit volume and per time, generated or released. The vector n is the outward unit normal on Γ.

The physical problem, we are concerned with, is to determine the internal boundary Γ_i from the temperature measurements φ performed on the external boundary Γ_e at specified points x_i (i = 1 to N_x) and discrete times t_j (j = 1 to N_t). We assume that there is a single cavity in the material and that its boundary Γ_i is assumed to be a simple closed curve. The input heat flux ϕ_e, the quantity Q and the constant T_i are well-known.

Such problems have been mathematically examined in 17,18 for the case Q = 0 and continuous flux and temperature measurements. The authors in 17,18 have used an identification approach based on the boundary element method. Moreover, an identification approach based on a finite element method, which is able to handle more general heat equation, has been proposed in 20.

In the present article, we consider:

•	Q ≠ 0 to take into account a non-negligible energy exchange with the exterior. Q can also represent a heat source, specially, introduced to improve the estimation quality;
•	discrete temperature measurements that is more realistic in practice, further, measuring a temperature is more easy and precise than measuring a flux;
•	physical values of thermal properties to point out their influence on the identification quality which cannot be seen if only dimensionless equations are being considered.

In addition, we propose an easy implementation of the identification algorithm with the help of the free finite element software FreeFem 21. This software allows the resolution of partial differential equations by writing few lines of code. Also, FreeFem provides some well-known optimization procedures (linear and non-linear conjugate gradient, Newton–Raphson, …) making it appropriate to handle, easily, inverse problems in partial differential equations.

3. Formulation of the approximate inverse problem

A numerical implementation requires a parametrization of the unknown boundary. We assume that Γ_i is starlike with respect to the origin. Therefore, it can be described by the following parametric representation: where r is the radial function satisfying r(0) = r(2π).

For numerical resolution, this radial function is approximated by trigonometric polynomials of degree less than or equal to K, i.e. where Setting and r_ex the radial function of the boundary Γ_e, then we define the set of admissible vectors by The problem of identification of Γ_i can now be set as: find in such a way that the calculated temperature by system (1) is close to the measurements φ(x_i, t_j).

Let A be the operator which associates to the vector , the function defined on Γ_e×[0, t_f] by: , where T is the solution of system (1) with the corresponding boundary .

In the classic way, the above identification problem is often formulated as a minimization of the following output least-squares criterion The term in β is introduced to deal with the ill-posedness of this inverse problem (second-order regularization) 22.

However, the operator is a function strongly non-linear, direct minimization of R can fail. Therefore, we opt for the iterative Newton method, mostly used in the domain of shape estimation 17–19,23. This method consists in linearizing and instead of minimizing , the following criterion (2) is minimized with respect to a new variable . Once is determined, is updated by and the new criterion is optimized. The process is repeated until convergence. The full algorithm will be presented in section 5.

In the next section, we will establish , the gradient of A which involves a domain derivation.

4. Gradient establishment

By definition where is the k-th element of the ℝ^2K+1 canonical base.

Let be the boundary corresponding to the vector . Its radial function is .

Then, , which is, in the domain derivative terms, a perturbation of the boundary in the direction a = q_k(θ)(cos θ, sin θ).

Strong calculations similar to those carried out in 17 lead to the following result:

Let v be the solution of the system (3) then (4) where a = q_k(θ)(cos θ, sin θ).

5. Numerical implementation

The systems of partial differential equations (1) and (3) are discretized by means of an implicit scheme in time with a step δt. The resulting equations are solved by the finite elements software FreeFem + + 21. Linear piecewise P1 or quadratic P2 functions are used. The domain D meshing is generated by dividing the boundaries Γ_i and Γ_e by integer numbers. The same number, N, is chosen in our case.

The minimization of is achieved by the FreeFem subroutine linearCG 21. This subroutine minimizes by computing the roots of the equation , using a conjugate gradient method. It requires an initialization of vector , a real ξ to stop the process when , and the expression of which is given by (5)

Finally, the identification algorithm can be summarized as follows:

1.	start with initial known vector and get ;
2.	solve the direct system (1) with parameters δt and N. This makes and the normal derivative (∂T/∂n) available;
3.	for each k (varying from 0 to 2K), set a = qk(θ)(cos θ, sin θ) and solve the system (3). This gives the gradient ;
4.	minimize (2), starting from a vector to yield ;
5.	make , if the stopping test is satisfied or the allowed number of iterations reach terminate; else go to 1.

As a stopping test, we take where .

6. Numerical tests

6.1. Measurements simulation

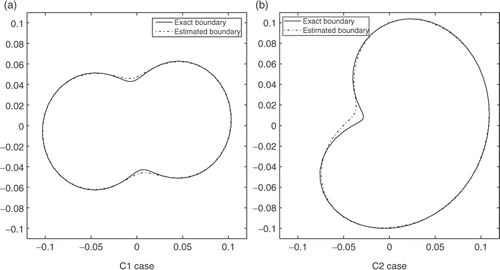
The measurements φ are simulated by numerically solving the direct system (1) with Γ_i characterized by a radial function r_*. Two boundaries, denoted by C1 and C2, and described respectively by are considered here.

We choose as material silver with its thermal properties ρc = 2.467(10⁶ Jm⁻³°C⁻¹ and λ = 420 (W m⁻¹ · C⁻¹).

The external boundary is the circle of radius R = 0.15(m) and centered at the origin. The boundaries conditions are T_i = 25 (°C) and ϕ_e(x, t) = 25(1 − exp(−t/100)) (kW m⁻²). We take the values of Q and time measurements t_f as 250t(W m⁻³) and 200(s), respectively.

The discretization parameters are δt = 10(s), N = 50 and P2 finite elements.

Once the temperature distribution T is available, the measurements φ are simulated by adding random errors as follows: φ(x_i, t_j) = T(x_i, t_j) + μσT(x_i, t_j) where μ is a random number in the interval [−1, 1], σ represents the magnitude of the errors, t_j = 10j (j = 1 to 20) and x_i = R(cos(θ_i), sin(θ_i)), , (i = 1 to 20).

6.2. Identification results

We try now to reconstitute the exact boundaries by the proposed inverse method. For this, systems (1) and (3) are solved with δt = 10 (s), N = 50 and P1 finite elements. We take 6 for the number of allowed iterations, K = 4 as a degree of the trigonometric polynomials approximation and 0.005 for the stopping test δ. The algorithm is initialized by the circle centered at the origin with radius of 0.1 (m). The subroutine LinearCG is initialized by with a stop test ξ = 0.0001.

As the function to be minimized, J_m(p), varies at each iteration m, the regularizing parameter α_m is also adapted. We choose, by trial and error, .

To quantify the identification quality, we define the relative error between the exact curve and the estimated one by: E = (|r − r_*|/|r_*|), where r is the radial function obtained by the inverse resolution.

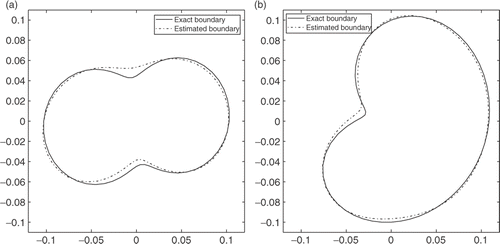
By considering, first, exact measurements (σ = 0), the identification algorithm converges after three iterations (m = 3). The obtained relative error is E₁ = 0.0138 for the curve C1 whereas for C2 this error is E₂ = 0.0352. Figure 2 depicts the estimated boundary and the exact one for C1 and C2 cases. The match between the exact boundaries and the estimated ones is good with relative errors less than 4%.

Figure 2. Exact and estimated boundaries comparison–exact measurements.

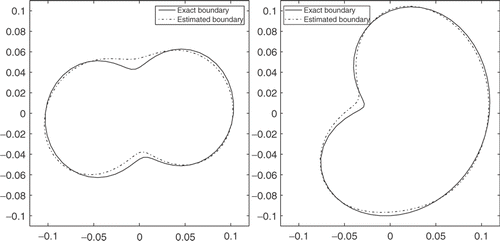
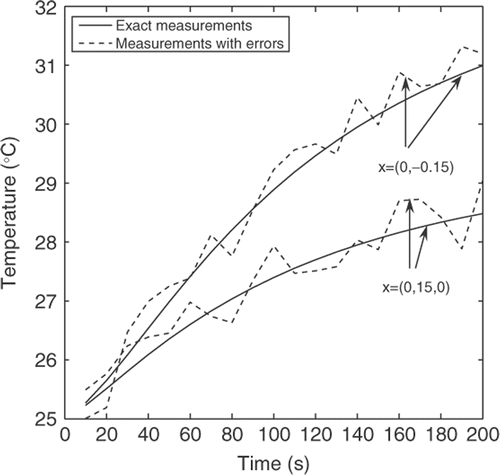
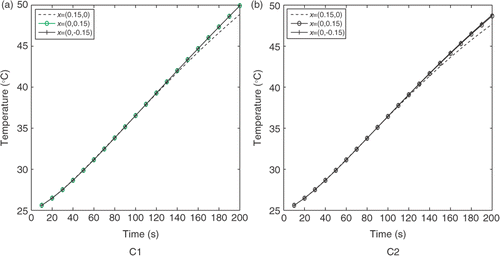
Now, considering, measurements with errors of 2%(σ = 0.02) figure 4 plots the evolution versus time of the simulated measurements (exact and with errors) at points x = (0.15, 0) and x = (0, −0.15), obtained with C1 curve. The identification algorithm always converges after 3 Newton steps. However the relative error E₁ increases significantly to 0.0531 while E₂ increases slightly to 0.0370. On the other hand, figure 3 shows that the identification, using measurements with errors of 2%, is also reasonably good.

Figure 3. Exact and estimated boundaries comparison–measurements with errors 2%.

Figure 4. Exact measurements and measurements with errors 2%.

If the errors in the measurements increase to 5%, the identification of C1 becomes difficult (E₁ = 0.1435) and that of C2 is still possible and good (E₂ = 0.0492). The sensitivity of C1 identification to the level of errors in the measurements is related to the distance between C1 points and the boundary where the measurements are performed, which is higher in the case of C1 compared to C2. To illustrate that, we multiply the radial function of C1 by a factor 1.2, the identification becomes possible and the relative error decreases considerably to reach 0.067.

6.3. Influence of material properties

The purpose of this section is to point out the influence of the thermal properties of the material on the identification. For this end, we consider materials: gold, silver, copper and steel, whose thermophysical properties are given in table 1. Noting that D_s = λ/ρc is the thermal diffusivity of the material.

Table 1. Materials properties

	ρc (10^6J m^−3.C^−1)	λ (W m^−1.C^−1)	Ds (10^−6 m^2 s^−1)
Silver	2.467	420	170.24
Gold	2.509	300	119.56
Copper	3.592	389	108.29
Steel	3.661	43	11.74

The previous identification process is repeated for each material and the obtained results are reported in table 2.

Table 2. The obtained relative errors–measurements with errors 2%

	Boundary	E
Silver	C1	0.0531
	C2	0.0370
Gold	C1	0.0431
	C2	0.0373
Copper	C1	0.0506
	C2	0.0328
Steel	C1	0.1072
	C2	0.1483

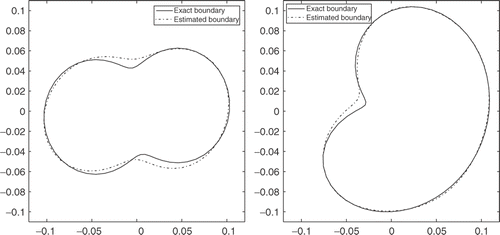
According to table 2, it can be concluded that for silver, gold and copper with high and comparable thermal diffusivity, the quality of the identification is practically the same. Noting also that the identification of C2 is more accurate than that of C1. Figure 5 indicates a good agreement between the estimated boundaries and the exact ones for copper case. Furthermore, for all these materials, the temperature varies between initial value 25 (°C) and a maximum of 32.5 (°C), which implies that the adopted linear model for the heat equation holds well.

Figure 5. Boundaries comparison–copper case, measurements with errors 2%.

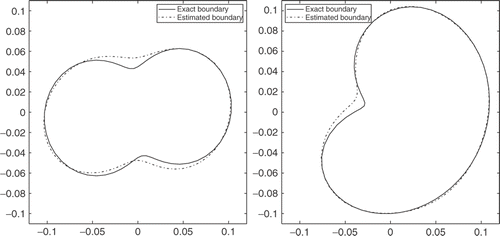
For steel, the quality of identification is bad for the considered horizon t_f and the applied heat flux. In fact, the effect of the inner boundary on the external temperature measurements necessitates time to appear, due to the low-thermal diffusivity of the material. In order to illustrate this, we plot on figure 6 the evolution, versus time, of the simulated temperatures at some specified points on the external boundary. As can be seen, the temperatures on all these points are the same over a wide interval of time ([0,120 (s)]), independently of C1 and C2. Beyond 120 (s) the sensitivity of the external temperature to the shape of the inner boundary becomes pronounced and maximal near 200(s), where the temperatures obtained with C1 and C2 are significantly different. However, in the case of silver, the effect of the inner boundary on the external temperatures begins to appear from 10(s) as shown in figure 4. When the measurements (with errors of 2%) are kept for longer time (t_f = 400 (s)), the proposed method, as shown in figure 7, leads to an accurate estimation of the unknown boundaries (E₁ = 0.0534 and E₂ = 0.0371). Moreover, the temperature measurements vary from 25 (°C) to 68 (°C) over [0,400 (s)]. If the linearity of the adopted thermal model risk to be compromised by this temperatures range, we can seek for an input heat flux which reduce this range. By taking for example, ϕ_e,2(x, t) = 25(exp(−t/50)(kW m⁻²), the considered curves can be identified with good accuracy as shown in figure 8 (E₁ = 0.0552 and E₂ = 0.0425), with a measurements range [25 (°C), 32.6 (°C)].

Figure 6. External temperatures obtained with steel.

Figure 7. Boundaries comparison–steel case, measurements with errors 2%, t_f = 400 (s).

Figure 8. Boundaries obtained with ϕ_e,2, measurements with errors 2%, t_f = 400 (s).

7. Conclusion and perspective

In this work, we have presented an identification problem of an internal boundary of a material from discrete temperature measurements performed only on the external boundary. We have set and formulated this problem as an optimization problem. We have then presented and implemented an algorithm to solve this optimization problem. This gradient-based algorithm used the domain derivative techniques and finite elements method. The numerical tests carried out show that the proposed method is able to estimate the internal boundary from temperature measurements with errors less than 2%. The quality of the identification decreases when the distance between the inner boundary and the points where the measurements are performed increases. In addition, the horizon time is to be kept in connection with the thermal diffusivity of the considered material. Seeking for optimal input heat flux which maximizes the measurements sensitivity to the shape of the inner boundary, for a given material and a given horizon time, is an interesting task. The case where the boundary to be identified is under a heat flux condition is also of interest and will continue from this work.