Abstract
This article presents a hierarchical scheme based on a staggered design optimization approach that can simultaneously achieve both real-time design of the optimum physical experiments needed for the characterization of the material under consideration and the material characterization itself. The approach assumes that mechatronically driven systems are available for exposing specimens to multidimensional loading paths and for acquiring the stimulus and response behaviour data. Material characterization is achieved by minimizing the difference between the experimentally acquired and the analytically predicted response of the system. At the same time, performance metrics of the material characterization process are used to construct the objective functions for the design of experiments problem at a higher level. An example is presented for the case of characterization of the linear elastic constitutive response of anisotropic materials while the best loading path for achieving this goal with a two degree of freedom loading machine is also determined in real time.
1. Introduction
Automated mechatronic systems capable of applying multidimensional loading and collecting specimen response data present two distinct and unique opportunities with regard to inverse data driven modelling. The first and more well-known opportunity is the exploitation of the experimental data for parameter estimation associated with models describing material constitutive behaviour. The second and more unexplored area is the dynamic-data-driven identification of the most appropriate design of experiments (in contrast to numerical experiments) required for the previous task in terms of their various characteristics including the specimen shape and the loading path to be applied. This article aims to describe a methodology that takes advantage of both of these opportunities in a synchronous manner.
Utilization of data-driven design optimization practices to determine constitutive behaviour parameters of materials under mechanical loadings has been traditionally based on experimental procedures with fixed architectures and no regard to how experimental designs may affect the quality of the material parameter estimation processes. However, the advent of multi-degree of freedom mechatronic systems capable of multidimensional mechanical loading Citation1–3, has introduced the potential of multiple designs for experimental processes to acquire the necessary behavioural data.
Motivated by the drive to demonstrate that it is possible to dynamically affect the manner by which data is gathered, in the present article we are proposing a hierarchical design optimization methodology that intertwines two successive and dynamic design optimization subprocesses. One is responsible for the traditional parameter estimation associated with the linear or non-linear material constitutive behaviour; the other is responsible for the non-traditional parameter estimation associated with the characterization of the loading path followed by a multidimensional loading frame. Essentially, this approach allows for the development of a dynamic data-driven application system (DDDAS) that adapts in a manner that satisfies two sets of objectives. The first set of objectives are those that relate to determining the material parameters and are based solely on physical performance measures of the analytical model selected to represent the constitutive behaviour of the material. The second set of objectives contains those that relate to determining the parametric characteristics of an experimental sequence as it is controllable from a multi-degree of freedom loading machine.
Here we introduce the idea of a meta-objective function that is constructed to express the performance of the constitutive model characterization optimization cycle employed in the previous step. Thus, the experimental design is generated dynamically as data is being acquired in a fashion that optimizes the performance of the lower level optimization employed for the material parameter estimation.
The article continues with a section that defines the proposed methodology. Subsequently, an application related to characterizing the elastic response of a composite material is described where the performance of the characterization process is defined in terms of the uniqueness and distinguishability of the obtained parameter set as a solution of a singular value decomposition (SVD) problem. An application example is described and the article concludes with a short discussion of the findings and the plans.
2. Hierarchical framework
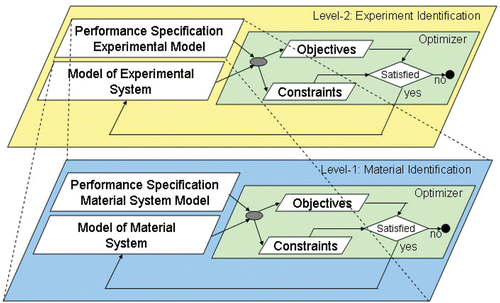
The hierarchical nature of the proposed framework approach is based on the observation that there are at least two layers of design optimization activities that could be involved in the activity of using experimentally obtained data to characterize a system.
As shown in , the lower level (level-1) is assigned with the more traditional task of identifying the parameters associated with the behaviour model in general, and the material constitutive model in particular. A performance specification for that model as well as the instantaneous snapshot of the behaviour of the model as it is instantiated from the previous set of material model parameters are used to from the optimizer's objectives (in terms of the related objective functions) and the corresponding equality or inequality constraints. In this particular performance specification of the material system model, it is usually required that the output of the under construction model has to be close to the actual experimental data expressing the same behaviour within a given tolerance.
At the higher (level 2) of this hierarchy, essentially all the components discussed in the lower level still exist, only in this case, instead of designing the material model, design optimization is utilized to design the experimental procedure, by determining certain parameters that characterize it. That is to say, the block (in ) referring to the model corresponds to the model approximating the experimental procedure itself. The block (in ) referring to the performance specification corresponds now to the performance specification of this experimental model.
The performance specification at this level can be defined in terms of objectives that maximize the quality of the determined model at the lower level and also maximize its computational performance. The necessary and sufficient condition for this to be possible requires the creation of objective functions at this level, that are expressed in terms of design variables that express quality features of the model determination at the lower level. These objective functions can further be endowed with measures of computational performance considerations such as fastest algorithm, highest accuracy, etc. Thus multi-objective function determination is implied here with at least two different partitions. One partition expresses the numerical performance of the lower level model and the other expresses the computational efficiency of the lower level model. For each acceptable determination of a model (establishment of a set of material model parameters), there is a set of values expressing the quality of the numerical and computational operations that depend on various decisions made (codified as design variable instantiation) directly related on how experiments are made. The fact that the overall performance of the lower level is used to define the performance specification at the higher level allows the consideration that the higher level is the design meta-level of the lower level.
3. General systemic preliminaries
In the general case of the lower level plane in , it is expected that a system under identification is described by some general form of the type:
(1)
where y∈Yqy⊆ℜqy,x∈Xqx⊆ℜqx represent the qy output and the qx input state variables, respectively, p∈Pp⊆ℜp represents the unknown vector of p parameters characterizing the system (that are also called design variables in the design optimization context), while
represents the vector function that encapsulates the behaviour of the system. An alternative representation of the systemic behaviour that is popular in continuum mechanics (and has its origins in the development of hyperelasticity) is the one that postulates the existence of the potential function Ψ(p; x) that
(2)
This formulation effectively endows the systemic representation with the efficiency of determining all components yu of the vector y from a single scalar potential function Ψ(p; x). An often forgotten assumption enabling this representation is the fact that the input and output variables correspond to each other and they form conjugate pairs of the form {yu, xu}, u = 1, …, q where q = qx = qy. In this case, the design optimization problem for level-1 is reduced to the determination of this function Ψ(p; x). A standard technique for determining this function involves its construction as an additive linear combination of basis functions β(x) weighted by the unknown coefficients p according to
(3)
where p = [p1, p2, …, pp] and β = [β1(x), β2(x), …, βn(x)]T. Another possible way to construct Ψ(p; x) originates from its thermodynamic nature (when it represents an internal energy density function for many continuum systems), that permits the employment of its Taylor expansion about the origin x = 0 with respect to the state variables represented by the base components of the input state subspace Xq. Expansion up to second order with respect to the variables xu will then yield a first-order constitutive theory according to Equation (2). Clearly when terms of higher than second order are employed, then the resulting systemic behaviour will turn up to be non-linear. When Equations (2) and (3) are inserted in Equation (1) we obtain a systemic behaviour model expressed as follows:
(4)
In the context of continua and their corresponding constitutive response, Equations (1–4) represent the behaviour of the medium regardless of its position within the geometry that encloses it, and is independent of its shape. However, for the sake of identifying the components of the parameter vector p, experimentally driven measurements are made on discrete location points i = [1, …, l] on the specimen/system where these measurements are made. At the same time excitation and response are measured in terms of input–output pairs for various magnitudes of excitation indexed by k = [1, …, m] for a total of m different magnitudes. Now we can construct a vector expressing the analytically produced behaviour of the system as
(5)
as well as the one from the corresponding experimental measurements as
(6)
The quantity
(7)
expresses the square of the L2 norm of the residual difference of the two vectors in terms of the least square difference of their respective magnitudes for each excitation increment. However, relation (7) has to be satisfied for all excitation levels m but also needs to be extended in order to include all discrete measurement positions l. This fact along with the introduction of Equations (4–6) into Equation (7) generalizes the former to the form,
(8)
Since this expression provides the definition of the residual error, it can be used to define that the objective function
when minimized yields the unknown parameter vector p. This would be representing the design optimization process to be performed at level-1.
When it is known that a linear constitutive behaviour can approximate the behaviour of the system, then it can be inferred from Equation (4) that β(x) has to be a second-order function of the components of x. In that case, it is trivial to show that Equation (8) can be reduced to a problem involving the determination of the scalar function Ψ(p; x) according to
(9)
where the overbar quantities correspond to the experimental values of the ‘work’-like function that corresponds to the inner product of the input and output vectors of the original system.
The problem expressed by Equation (9) can be solved by either the ‘normal equations’ method or the ‘QR factorization’ method or the ‘singular value decomposition’ (SVD) method Citation4. Selecting one of these methods to determine the unknown model parameters can be a process that depends on ranking these methods with regard to their performance in terms of attributes or metrics that are important to the user. It has been documented, for example, that the normal equation method is computationally fast and requires less resources but is less accurate. At the same time it is known that SVD requires the most computational resources but is more reliable than the rest. It is natural therefore, to ask the question how these attributes might vary if the user has control of the characteristics that determine the particular choice made for experimental data used to populate all column arrays with the upper right naming extension ‘e’ (that denotes experimental value) in the relations presented above.
4. Composite material system
For demonstration purposes we consider a linear anisotropic material with the four moduli expressing its constitutive characteristics. We have already demonstrated Citation5, Citation6 that this problem can be reduced to the following linear (with respect to the unknown parameter vector) relation
(10)
where
is a m × 4-dimensioned array that contributes the finite element approximation of the internal energy stored in the system from an increment of strain from point k − 1 to point k in a manner that does not contain the material moduli since that is contributed by the 4 × 1 array qM of the unknown parameters on the left-hand side of Equation (10). In the right-hand side, the m-dimensioned array wk = [W1/t, …, Wn/t]T contains the external work that is applied as excitation into the system for all loading increments.
In Equation (10), the right-hand side represents the measured output of the system, while the left-hand side represents the corresponding changes inside the system due to all possible excitation inputs. Its solution can be approached as a special case of the problem presented by Equation (9) and can be achieved by using any of the three methods available for implementation of least-squares approximation.
While selecting among the various methods it may implicitly suggest the idea of yet another optimization level, here we will focus on using SVD for the purpose of determining the parameters of the material model associated with level-1. We will also neglect additional computational performance criteria and focus only on potential measures of performance of the SVD implementation from an algorithmic perspective.
Thus, the solution containing the identified parameters according to Equation (10) can be written in the form
(11)
where
(12)
is the pseudoinverse of G(θ) and it exists uniquely only when n ≥ 4 or when the system of linear equations represented by Equation (11) is overdetermined (more equations than unknowns).
5. Level-1 performance measures
What determines the quality of solving Equation (10) is now reduced to determining the quality of applying Equation (11) and therefore the quality of the process associated with establishing the pseudoinverse array defined by Equation (12).
We have identified in the past Citation6, Citation7 that the two concepts of ‘uniqueness’ and ‘distinguishability’ of the obtained solution can be used as performance metrics for the determination of the parameter column array qM.
In order to define these two concepts we need to focus on a few preliminaries relating the singular values of the SVD process to the problem at hand. In particular, the uniqueness of the solution depends not only on the size of G(θ) but also on whether G(θ)T G(θ) in Equation (12) has and inverse matrix [or this matrix is fully ranked (r = 4)]. In order to guarantee the uniqueness and further prepare for designing optimal experiments via level-2 optimization, the proposed technique obtains the singular values of the matrix as a result of SVD Citation7, Citation8 as they express the factorization of in the form:
(13)
where U∈ℜn × n and V∈ℜ4 × 4 are orthogonal to each other and S∈ℜn × 4 is a diagonal array with real, non-negative singular values si, ∀i ∈ {1,…, 4}. These singular values can be used to define the two measures characterizing parameter identification, one being the distinguishability and the other being the uniqueness of the solution and are described as follows.
From a conceptual perspective, distinguishability can be defined as the property of the obtained solution to provide the largest possible variation of the measured response of two systems when their material parameters are very close to each other.
It has been demonstrated that when two materials systems exhibit a small difference in their properties, then the difference of the values of their corresponding responses (observed experimentally) depend linearly on S Citation6–8. Accordingly, any expression of the combined effect of the elements of S as it increases has the ability to distinguish two materials that are seemingly close to each other from a properties perspective, by producing exaggerated energy responses that are scaled values of these property variations.
From a quantitative perspective, we have defined distinguishability as the product of all singular values as,
(14)
From a conceptual perspective uniqueness has been defined as the measure of whether G(θ)T G(θ) in Equation (12) has an inverse matrix or not, is equivalent to the existence of (STS)−1 as shown by substituting Equation (13) into Equation (12) that yields
(15)
The necessary and sufficient condition for this to occur is given by
(16)
i.e. si ≠ 0, ∀i ∈ {1, …, 4}. In addition to helping identify the uniqueness, singular values can also be used to quantify the degree of uniqueness of the solution. This is because a non-zero but near-zero singular value, if it exists, dominates the elements of the pseudoinverse matrix (15) and makes the parameters with the other singular values difficult to identify uniquely. Such degree of uniqueness can be conclusively described by the fact that the less indifferent the singular values are from each other, then the more unique (i.e. higher uniqueness) the solution is.
One way to define uniqueness quantitatively requires the introduction of the concepts of maximum and minimum singular values
(17)
and evaluate deviation from uniqueness in terms of the condition number c, which is commonly used in sensitivity analysis as:
(18)
It is important to underscore here that distinguishability increases as any of the si increases, while uniqueness increases as the condition number decreases to unity.
6. Level-2 optimization
If in addition to determining the material parameters we require that this is achieved such as distinguishability and uniqueness are as high as possible, then we have instantly defined the goals of the level-2 optimization. The design variables at level-2 have to therefore be connected with what is controllable in an experimental setup used to acquire experimental data used for identifying the material parameters at level-1. Such parameters can be those that define the evolution of the loading path, such as total number of increments, loading path increment magnitude and loading path increment orientation. For the case of a displacement-controlled two degree of freedom (2-DoF), testing machine used for experimentation the parameter vector to be identified per loading increment could be formed by the measure of displacement increment
(19)
and the angle denoting the change orientation of the loading path between two successive increments is defined as
(20)
with the total boundary displacement vector defined by its components along the two axes according to the usual definition uk ≡ [ux, uy]k = [ux|k, uv|k]. In the subsequent analysis, we will assume constant displacement increment of a chosen magnitude and the parameter to be optimized against will be just the load path directional change Λk,k+1 for all increments. Since increased uniqueness and distinguishability both express a sense of reliability of the SVD process used for determining the material parameters in level-1, we can define a vectorial objective function that needs to be maximized for maximum reliability. It is constructed such as
(21)
where the objective function components
represent the corresponding increments of distinguishability and uniqueness along an increment of loading according to
(22)
The distinguishability and uniqueness are computed through the derivation of the matrix G(θ) in Equation (10). In order to compute the matrix G(θ) is assembled for the sensor readings at load increment k, through the derivation of the alternate form of Equation (10) Citation6–8:
(23)
The distinguishability and uniqueness up to step K + 1 are predicted from the matrix with the additional row:
(24)
where
and
are computed via finite element analysis (FEA) with the controllable boundary displacements/forces governed by ΛK,K + 1 and by using the material parameters (elastic moduli for this case) identified up to now. This represents a 1-step look-ahead computation relative to the activities of level-1 as they relate to those of level-2.
Throughout this article the symbolic representation is used to represent the quantity ( · ) as it is associated with FEA.
As expected, the solution of the two objective functions problem is not given by a single point but by a space satisfying the Pareto-optimality, which is often referred to as Pareto-optimal front Citation6–8. This formulation requires the derivation of a Pareto-optimal front prior to the determination of a single solution and this is extremely time-consuming from a computational perspective. Because of this reason and assuming that the Pareto-optimal front would be convex or near-convex, the problem can be reformulated in a manner that only one scalar objective function is constructed according to the following generalized form
(25)
where each objective function is given by the scaled increment:
(26)
and μ ∈ [0, 1] is a weighting factor that controls the bias towards one or the other component of the objective function. The formulation expressed by Equations (25) and (26) avoids the derivation of the Pareto-front.
7. Numerical examples
For the sake of numerical demonstration of the proposed concepts, the material selected for generating the necessary simulated experimental data is a typical laminate constructed from an epoxy resin/fibre laminae system of type AS4/3506-1 with a balanced +/–30° stacking sequence. The elastic moduli of this material are listed in .
Table 1. Moduli of AS4/3506-1 laminae.
All subsequent computational results have been produced by the implementation of the analysis presented earlier within MATLAB Citation9.
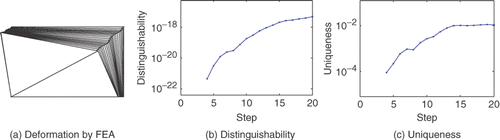
shows the deformed stages of a simple rectangular plate made from the specified material and displaced under the influence of an undulating loading path for a sequence of 20 increments in this path. Distinguishability and uniqueness are increasing with increasing load step increments in and , respectively.
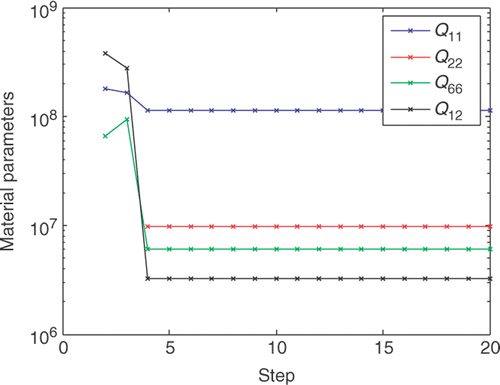
We have already discussed elsewhere Citation6, Citation7 the fact that an undulating path (ux displacement component is non-monotonic), maximizes distinguishability and uniqueness more efficiently than a uniaxial loading path along the y-direction (that cannot actually determine all unknown material parameters) or a linear path with monotonic ux and uy displacement components. depicts the results of the material moduli determination as a function of loading steps for the loading path represented by . This represents the results achieved during level-1 optimization.
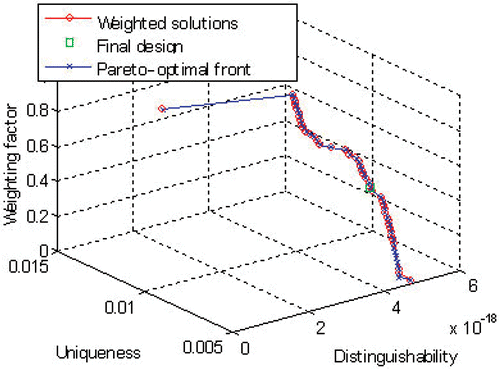
presents the results of performing the level-2 optimization as described earlier, in terms if the evolution of the Pareto-optimal front as defined in terms of distinguishability and uniqueness for a the entire range of the weighting factor μ ∈ [0, 1].
The choice of the optimal solution corresponds to setting μ = 0.5 because this choice balances the contribution of each one of the original objective functions on the global one as expressed by Equation (25).
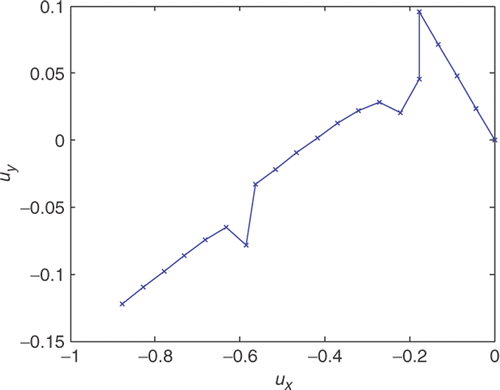
The resulting solution for level-2 optimization is expressed in terms of the loading path defined on the ux– uy plane as shown in .
8. Conclusions and discussion
The preliminary framework of a general hierarchical methodology was proposed; this methodology can succeed in both the determination of the parameters characterizing the response of a system, as well as characterizing the design parameters of an experiment required to collect data necessary for the systemic characterization.
The approach was applied in the context of an anisotropic material system. The systemic constitutive response of a linear anisotropic behaviour to be identified was selected to be the elastic system fully defined from its five elastic moduli. These were the design variables for the first hierarchical optimization level (level-1). The experimental model needed to be considered for the second optimization level (level-2) was chosen to represent the description of a loading path in a 2-dimensional loading space. Implied here is the existence of a 2-degree of freedom loading frame, capable of applying such a loading path and measure both the path and reaction mechanical load characteristics for each increment.
To achieve a definition of the objective function at level-2, the quantities of distinguishability and uniqueness were introduced as performance metrics of the design optimization process at level-2 that quantifies the performance of the SVD process employed. To achieve this, a two-component meta-objective function was constructed to be maximized. Maximization of this dual objective function leads to the creation of a Pareto-front that ultimately contains the loci of all acceptable solutions that can be used to determine dynamically the experimental design specification in terms of loading path direction parameter.
Numerical simulation of the entire process was performed to demonstrate its feasibility. We demonstrated that the material moduli unknowns can be determined simultaneously to the loading path characteristics needed to design the necessary experiment for collecting the data needed for level-1.
Clearly, the question of ‘how good the design optimization for level-n is’ from the perspective of the optimization of level-(n + 1) is valid for all subsequent levels, a user wishes to employ. This effectively extends the hierarchy upward. Practicality and total computational cost will eventually have to appear in these objective functions and the hierarchy's extension will eventually have to stop. This will also determine the throughput capability of the entire process from a DDDAS perspective. Various extensions of this type will be attempted in the future, while simulation as the activity of exercising the determined model will also be added to complete the essential triad (dynamic and simultaneous physical model identification, design of experiments and design of simulation) of activities associated with a DDDAS Citation10.
Acknowledgements
The authors acknowledge the support by the Office of Naval Research and the National Science Foundation under grant 0540419. Partial support from NRL's 6.1 core-funding is also acknowledged.
References
- Mast, PW, Nash, GE, Michopoulos, JG, Thomas, R, Badaliance, R, and Wolock, I, 1995. Characterization of strain-induced damage in composites based on the dissipated energy density, Theor. Appl. Fract. Mech. 22 (1995), pp. 71–125.
- Michopoulos, J, 2004. Mechatronically Automated Characterization of Material Constitutive Response, Proceedings of the 6th World Congress on Computational Mechanics (WCCM-VI), 5–10 September 2004. Beijing, China: Tsinghua University Press and Springer; 2004. pp. 486–491.
- Michopoulos, J, 2003. "Computational and mechatronic automation of multiphysics research for structural and material systems". In: Gdoutos, EE, and Marioli-Riga, ZP, eds. Recent Advances in Composite Materials. Xanthi: Kluwer Academic Publishing; 2003. pp. 9–21.
- Lawson, CL, and Hanson, RJ, 1974. Solving Least Squares Problems. Philadelphia, PA: Reprinted 1996 by SIAM Publications; 1974, Prentice-Hall, Englewood Cliffs, NJ.
- Michopoulos, JG, Furukawa, T, and Kelly, DW, A Continuum Approach for Identifying Elastic Moduli of Composites. Presented at Proceedings of the 16th European Conference of Fracture. Alexandroupolis, Greece, 2006.
- Michopoulos, JG, and Furukawa, T, 2006. "Effect of loading path and specimen shape on inverse identification of elastic properties of composites". In: Proceedings of IDETC/CIE 2006 ASME 2006, Paper DETC-2006-99724, CD-Rom ISBN: 0-7918-3784-X. 2006.
- Furukawa, T, and Michopoulos, JG, Design of multiaxial tests for characterizing anisotropic materials, Int. J. Numer. Meth. Eng, (in print).
- Furukawa, T, and Michopoulos, JG, 2008. Dynamic data-driven scheduling of multi-axial experiments for the elastic characterization of anisotropic materials, Comp. Methods Appl. Mech. Eng. 195 (2008), pp. 885–901.
- The Mathworks, Matlab, Available from http://www.mathworks.com.
- Darema, F, 2006. Introduction to the ICCS2006 workshop on dynamic data driven applications systems, Int. Conf. Comp. Sci. 3 (2006), pp. 375–383.