Recovering the source term in a linear diffusion problem by the method of fundamental solutions

Abstract

This work considers the detection of the spatial source term distribution in a multidimensional linear diffusion problem with constant (and known) thermal conductivity. This work can be physically associated with the detection of non-homogeneities in a material that are inclusion sources in a heat conduction problem. The uniqueness of the inverse problem is discussed in terms of classes of identifiable sources. Numerically, we propose to solve these inverse source problems using fundamental solution-based methods, namely an extension of the method of fundamental solutions to domain problems. Several examples are presented and the numerical reconstructions are discussed.

Keywords:

• inverse problems
• meshfree methods
• fundamental solutions
• heat source detection
• characteristic sources

AMS Subject Classifications:

• MSC 65N35
• 35J25
• 80A23

Nomenclature

Φ0	=	fundamental solutions for the Laplace equation
Φ00	=	fundamental solutions for the Bilaplace equation
Φκ	=	fundamental solutions for the Helmholtz equation
Φκ	=	Bessel functions of the first kind
xp	=	domain collocation points
yj	=	source points on an auxiliary boundary outside the domain
zj	=	source points inside the domain

1. Introduction

The problem of source reconstruction from boundary measurements for the Laplace operator, and more generally in elliptic problems, has been studied by several authors (see for instance 1 for an overview on the subject). In general, this inverse source problem lacks the uniqueness and some extra information about the unknown source must be considered. Since intrusive measurements are to be avoided (e.g. 2), in order to obtain uniqueness we have to restrict the sources to some a priori knowledge (e.g. 3,4). To this purpose we assume the source to be known in some class:

i.	linear or affine classes, for instance, defined as the inverse image of certain elliptic operators on some known function;
ii.	non-linear classes, where uniqueness has been proved, for instance, sources defined as characteristic functions of star-shaped sets (uniqueness was established by Novikov 5).

The full knowledge of the Dirichlet–Neumann map, which in the experimental framework means to formulate different boundary value problems and overdetermine the reconstruction problem with the same unknown internal source, does not increase the existing information about the source with a single measurement. We present an example for which two different internal sources, in different classes, may create the same boundary Cauchy data. With a restriction in the class of admissible sources, in the reconstruction problem, it is possible to determine the source from the boundary Cauchy data if some a priori knowledge on the type of internal source is assumed. For instance, it is possible to recover a characteristic function for star-shaped sources, as mentioned above, using a remarkable early proof, by Novikov 5 in the 1930s. More obviously, from a single boundary measurement it is possible to recover an harmonic source, or a source which consists of a product of a known function and an unknown one (such as the base and the height, cf. 3).

In this article, we prove that we can identify classes on which the inverse problem has unique solution and that in particular, the harmonic part of a source can be recovered from the boundary data. Thus, the identification of sources on admissible classes is proven to be equivalent to the identification of the harmonic part.

To numerically solve the inverse problem, we present numerical methods based on methods of fundamental solutions (MFS or MFS-D). The MFS is a numerical method that allows to compute the solution of boundary value problems for a partial differential equation whenever its fundamental solution is known. The first contributions to this field can be dated back to the 1960s with Kupradze and Alekside 6 – for an overview, a good reference still is Fairweather and Karageorghis 7. However, due to ill conditioning problems and to the development of other classical methods, the MFS was misregarded although there were some mathematical results that justified the excellent numerical simulations for smooth data 8. Over the last decade, the advantages of the MFS as a meshfree method with simple computational implementation have been recognized and further developments have been made. The MFS has been used in the past as a tool for inverse problems (IP), mainly as a solver for Cauchy problems (for instance, in the Kirsch–Kress method for exterior IP, e.g. 9).

An extension of the MFS to non-homogeneous problems, the MFS-D has been presented in 10 (see also 11). In this work, we apply the features of the MFS-D to the treatment of inverse source problems as initially discussed in 12. The idea is exactly to use the fundamental solution of the Helmholtz equation to obtain particular solutions that fit in a class where uniqueness has been proved.

2. Inverse problem

Consider a finite medium Ω, with constant thermophysical properties, subjected to a prescribed temperature at the boundary ∂Ω. Further, we will assume that Ω is open and simply connected (i.e. with no holes in its interior) and with regular (at least C¹) boundary ∂Ω.

The direct problem consists of the determination of the temperature inside the body, and the correspondent heat flux on the boundary. The temperature T in the body is generated by a source g in the interior of Ω and a prescribed temperature T₀ on the boundary of the medium (Dirichlet boundary conditions). The governing boundary value problem is a Poisson problem (1) To simplify the inverse problem, we assume the thermal conductivity K to be constant and known. The solution T of this problem is unique in H¹(Ω) for any given g ∈ L²(Ω) and T₀ ∈ C(∂Ω) ⊂ H^1/2(∂Ω) (e.g. 13).

H^s(X ) denotes the classical Sobolev spaces in a domain X = Ω ⊂ ℝ² or in a boundary X = ∂Ω (e.g. 14).

A similar direct problem would consist of considering the Neumann (or mixed) boundary conditions, imposing a compatible flux and measuring the temperature on a part of the boundary. Without loss of generality, we will consider only the Dirichlet problem.

The inverse problem consists of recovering the source g, from the prescribed boundary temperature T₀ and measured heat flux on a part of the boundary Γ ⊆ ∂Ω, given by the Neumann data (2) Schematically, we consider the direct (DP) and inverse (IP) problems in the following directions For simplicity, we assume henceforth that K = 1. In a previous paper by Colaço et al. 2, g was estimated by using intrusive measurements in a one-dimensional transient problem, through the conjugate gradient method with adjoint problem technique (e.g. Alifanov 15, Ozisik and Orlande 16). Using that technique, the recovery of the source term using only measurements at the boundary was unsatisfactory and intrusive measurements were needed. In this article, we aim to obtain g by using only non-intrusive measurements.

2.1. Uniqueness

We start with an example that shows some limitations in the recovering of general sources from the Cauchy data.

2.1.1. Non-uniqueness results for a general source

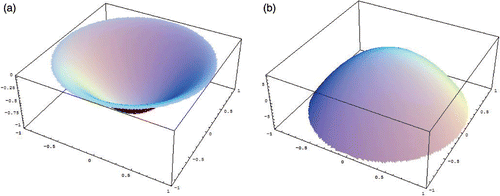
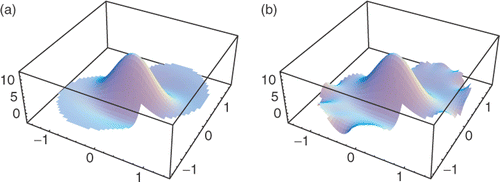
It is known (e.g. 1,3) that the inverse problem of recovering a general source g from Cauchy data is not well-defined. For instance, consider the temperature distribution (3) and the domain Ω = B(0, 1) the unitary circle with boundary ∂Ω = {x ∈ ℝ² : ‖x‖ = 1} (see the plot of τ in Figure 1). Then, (4) (5) (6) This means that for a non-null and regular source g_τ(x) = −16‖x‖² + 8, we can have null Cauchy data on the boundary ∂Ω. In this case, it would never be possible to recover this source from the boundary data (7) and this means that we cannot distinguish between a true source g and another source g + g_τ since the boundary data are always the same – no matter the number of different boundary conditions are to be considered.

Figure 1. Counter-example on uniqueness: the solution τ (a) which verifies null Cauchy data and the source g_τ (b).

2.1.2. Uniqueness in linear classes

The previous counter-example shows that some a priori knowledge of the source g must be made in order to recovery it. In a simple approach, we may assume that g belongs to simple linear classes. These cases are also relevant since we may assume that g = f − f₀, where f₀ is a known source and f is the result from an unknown variation in the original source. Therefore, the variation g might be considered in a simple class.

One simple possibility is to assume that the source (or the source variation) g satisfies some differential equation, for instance Δg = λg + F, with known λ ≥ 0 and F ∈ L²(Ω) – being the simplest case here is to consider λ = 0, F = 0, which means that the sources (or the source variation) are harmonic.

Then, we can consider the Bilaplacian type of problem (8) However, in order to obtain well posedness for this fourth-order problem, the boundary data regularity has to increase. The proper functional setting is now T₀ ∈ H^3/2(∂Ω) and Q ∈ H^1/2(∂Ω).

THEOREM 2.1

If the source function g belongs to the linear class 𝒞(λ, F ) with (9) then it is uniquely identified from the Cauchy data on ∂Ω.

Proof

Suppose that for T₀ ∈ H^3/2(∂Ω), two given sources g₁, g₂ ∈ 𝒞(λ, F) generate the same Neumann data Q ∈ H^1/2(∂Ω). Denote by T_i the solution of Poisson's equation ΔT_i = g_i with Cauchy data (T₀, Q), i = 1, 2. Then, for T = T₁ − T₂ we have ΔT = ΔT₁ − ΔT₂ = g₁ − g₂ and (10) By the well posedness of this problem, we have T = 0 on Ω hence,

Remark 1

From the previous counter-example, we see that Δ²τ = −64 and therefore, g_τ would be the unique solution in the class of sources 𝒞(0, −64) that verifies null Cauchy data on the boundary (note that the null solution is excluded because g = 0 would belong, for instance, to 𝒞(0, 0) but never to 𝒞(0, −64)).

2.1.3. Uniqueness in non-linear classes

A well-known inverse source problem consists of the determination of a source defined by a characteristic function χ_ω, defined to be 1 in ω and null elsewhere. For two different sets ω₁ and ω₂, the characteristic function of the union is given by the disjoint sum of the characteristic functions χ_ω1∪ω2 = χ_ω1 + χ_ω2 − χ_ω1∩ω2.

However, no relation is available between the multiplication by a scalar αχ_ω and a characteristic function χ_A(ω) and this class does not present a linear behaviour.

In the 1930s, Novikov (5 see also 1) proved a uniqueness identification result for the class of characteristic functions (11) from the Cauchy data on the whole boundary.

Remark 2 (Source identification from partial data).

The knowledge on the whole boundary can be dropped for compactly supported sources. Suppose that Γ ⊂ ∂Ω is open in ∂Ω and that g has compact support ω ⊂ Ω (which is the case for characteristic functions). Then, by Holmgren's theorem and analytic continuation, the knowledge of the data (T₀, Q) on Γ, fully determines the solution in Ω₀ = {x ∈ Ω : g(x) = 0} ⊂ Ω. This means that from the knowledge of the Cauchy data on Γ we may reconstruct T in the open set Ω₀ and therefore, we get the Cauchy data on the whole ∂Ω(⊂ ∂Ω₀).

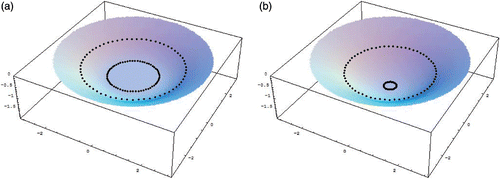
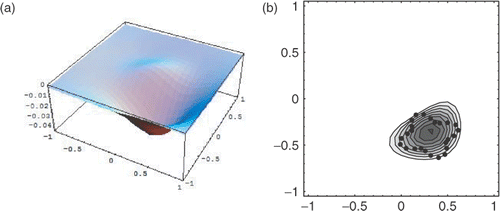
A star-shaped set can be defined from an internal point and an angular positive function that defines the radial coordinate in that angle. For characteristic functions defined on a general sets ω (including, for instance, annular sets) it is well known that the identification is not possible. Based on previous works (17 or the analysis in 3), we present an explicit counter-example in an annulus characteristic set (Figure 2) by taking (12) This is a C¹[0, c] function that verifies the radial Laplacian u ″(r) + u ′(r)/r = χ_[a,b]. 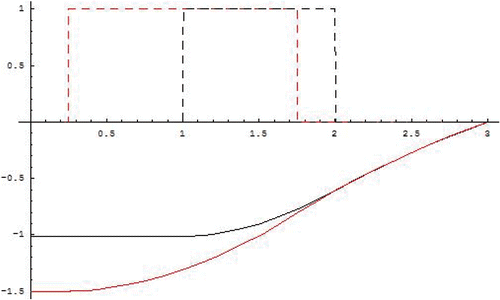Therefore, (13) is a solution of the problem (14) and we cannot recover a and b from the Neumann data on ∂Ω, which is constant in the external circle It is now clear that the single equation Q = racab² − a²2c cannot give both a and b, for instance, taking c = 3, we will have for both pairs (a, b) = (1, 2) or (see Figure 3 for the radial profile of T_A on both cases).

Figure 2. Counter-example: solution on the annulus (a) (a, b) = (1, 2), (b) .

Figure 3. Counter-example: radial profile of the solution T_A and the characteristic source.

2.2. Identification of a source from the harmonic part

We already established in Theorem 2.1 that harmonic sources, in the class ℋ(Ω) = 𝒞(0, 0), can be uniquely identified from the boundary measurements. On the other hand, we can see that from the knowledge of the harmonic part of the source we can recover the source, if the uniqueness is established for the same boundary data.

Using Green's theorem, we get the well-known decomposition (e.g. 18) (15) Thus, for any g ∈ L²(Ω), from (15), we have (16) with h_g ∈ ℋ(Ω) and w_g ∈ H₀²(Ω). On the other hand, being T the solution of the direct problem (1), we get (17) and since w_g = 0, ∂_nw_g = 0 on ∂Ω, we see that U = T − w_g verifies the auxiliary (well-posed) Bilaplacian problem (18) and we get the following result.

THEOREM 2.2

Let U be the solution of the Bilaplacian problem (18). Then, the harmonic part of g is h_g = ΔU. Moreover, the harmonic part of two sources coincides if and only if the Cauchy data coincides. In particular, the source is fully identified by its harmonic part (in a class where uniqueness is established).

Proof

The first part is a consequence of the arguments above, since h_g = Δ(T − w_g) = ΔU and Δ²U = Δh_g = 0.

For the second part, given the same Cauchy data then (18) produces the same U and therefore, the same harmonic part ΔU. Finally, if the harmonic part is the same ΔU₁ = ΔU₂, and since the Dirichlet boundary condition is fixed to be equal, U₁ = U₂ on the boundary ∂Ω, by the well posedness of the Dirichlet problem we have U₁ = U₂ in Ω and therefore ∂_nU₁ = ∂_nU₂, which means that all the boundary data coincides.▪

3. MFS-based methods for source reconstruction

3.1. Reconstruction of sources in 𝒞(0, 0) with the MFS

To solve the fourth-order problem (18) we use the MFS, which consists of representing the solution of terms of the functions (classical approach for the direct problem, e.g. 7,8) where Φ₀₀ and Φ₀ are the fundamental solutions of Bilaplace and Laplace operators, respectively and is a regular curve, enclosing the domain, . In the 2D case, (19) Thus, we write, in the discrete form (20) and compute the coefficients by imposing on the boundary the conditions (21) The previous system is solved in a least squares sense, for the general case. These systems are similar to the ones arising in the MFS, which are known to be ill-conditioned (e.g. 10), therefore a Tikhonov regularization parameter can be used.

Then, from the identity ΔΦ₀₀ = −1/(2π) + Φ₀, the harmonic part of the source is given by (22)

3.2. Reconstructions in 𝒞(0, F) – a method with Helmholtz particular solutions (MFS-D)

Generally, the IP can be addressed with the use of particular solutions u_κ of the Helmholtz equations (cf 10,11) (23) for some chosen wavenumbers κ. Taking several particular solutions of these equations, this simplifies the Laplacian to and therefore by writing (24) we immediately get (25) hence, we may try to recover from the knowledge of the coefficients α_κ,j in (24) obtained by fitting the Dirichlet and Neumann boundary conditions. To fit the expansion in (24) to the boundary data, we also use the particular solutions where Φ_κ is the fundamental solution of the Helmholtz equation, which is given (in 2D) by (26) Here is the first Hänkel function, defined by the Bessel functions of first and second kind (J₀ and Y₀, respectively). The full form of the fundamental solutions leads to singularities and the points y_j are to be considered on an auxiliary boundary outside the domain Ω.

However, since J₀ is non-singular, we may consider the imaginary part (27) as particular solutions centred in points z_j inside the domain Ω.

3.3. Direct application of the MFS-D

Therefore, in a general approach, we consider (28) where φ_α is a basis function that verifies (29) (this includes not only the possibilities φ_α = Φ_κ but also φ_α = Φ₀, with an appropriate choice of source points z_i).

To compute the coefficients α_i,j we impose on the boundary, the conditions (30) The approximation of the source is then given by (31)

3.3.1. Class of sources – direct application of the MFS

The previous general method gives a recovery of g in terms of a particular class when the coefficients α_κ,j in (24) are fitted to the boundary conditions. Therefore, it strongly depends on the choice of frequencies κ and particular solutions

Suppose that given T₀ and Q the coefficients in (24) were for some specific set of frequencies and particular solutions. Then, the sources to be recovered will be in the class (32) because (33)

Remark 1 (Particular case).

When the source g is known to be in a class 𝒞(0, λ²), then a single frequency λ will be sufficient in (24) because (34) and from we know that g is the unique solution in that class. Even if the frequency λ is not known, a good approximation can be obtained if our choice of frequencies is near the correct one.

3.4. Adding restrictions

The previous approach follows the initial work presented in Colaço et al. 12, and without imposing any extra conditions the solution will be in the class defined in (32). This can be a first approach if no a priori knowledge is given on the source. However, if we know that solution is unique in a certain class of functions we may restrict the solution to the appropriate class by adding restrictions to the coefficients α_i,j appearing in (30).

3.4.1. Harmonic part

If one seeks a harmonic source g, we have to impose (35) on some prescribed set of points x_p ∈ Ω.

Of course, another hypothesis is to consider φ_α only with α = 0, 00 as previously discussed in Section 3.1.

Remark 2

The same approach can be taken if we consider intrusive measurements, as in 2. This means that if we are able to measure T(x_p) in some internal points x_p ∈ Ω then the coefficients β_i,j will be restricted by the condition (36)

3.4.2. Characteristic source

For the identification of sources defined by characteristic functions (star-shaped sets) g ∈ 𝒞*, instead of (35) we consider the restriction (37) taking in account that for x_p near the boundary ∂Ω, this sum is zero – the support of the characteristic source is always inside the domain.

On the other points, since we do not know the result (otherwise we would know the source), we considered a relaxed restriction with every small ϵ and random ϵ_p : 0 ≤ ϵ_p ≤ ϵ.

4. Noise and regularization

4.1. Noisy data

In the following numerical simulations, we will consider noisy data on the measurements. These data are artificially generated from the true value Q by adding a random variable ϵ. It is common to test the methods with pointwise relative noise, using (38) with random values ‖ϵ_i‖ < ρ. In this situation, 100ρ is called the percentage level of relative pointwise noise. This pointwise noise is a sort of noise simplification since it means that the noise follows the solution, and almost no noise will be considered at the locations for which Q is small. To better simulate real noise, we also need to consider some amount of absolute noise, using the notion of norm noise. Instead of Q_R we will also consider (39) that depends on the considered norm p. If we take the ‘worst norm’, which is p = ∞, then even at the points where Q is small we can have perturbations as high as in the largest values of Q. We also considered noise following a Gaussian distribution, i.e. Q_N (x_i) = Q(x_i) + ϵ_i, where , with known mean μ and variance σ².

4.2. Boundary data and regularization

While considering the recovery problem in the linear class 𝒞(λ, F ), the ill–conditioned IP is transformed into a direct problem. However, this direct problem is not well-posed in the same functional spaces. For instance, in the inverse source problem for the Laplace equation we considered measurements Q = ∂_nT in the space H^−1/2(∂Ω). Then, in the transformed framework, the direct Bilaplacian problem is well posed for Q ∈ H^1/2(∂Ω), which means that some higher regularity is to be assumed in the measurements. Since noisy data are to be considered, then the measurements Q are not even continuous and no such regularity exists. This remark is important to notice that the ill-posedness of the problem did not vanish while transforming the IP into a higher-order direct problem.

To circumvent the regularity problem in the transformed higher-order framework, the measured data could be regularized using a filter function σ, such that the new data, given by the convolution would be at least continuous. Instead, we will consider a different process. Beside imposing the internal conditions inside the domain, we will extend these conditions up to the boundary. Therefore, the solution will not be too affected by the noisy data, since it is constrained with this other ‘boundary’ condition. With this extra condition, the noise oscillations are just in one of the three conditions now imposed on the boundary, and this regularizes the noise effect.

5. Numerical simulations

Since we used simulated measurements, obtained from the solution of the direct problem for a known source term, the values obtained for the direct problem were given by a domain decomposition method, with no relation to the fundamental solutions used in the methods for the IP.

5.1. Linear case

We start with two numerical simulations addressing the recovery of the source in the linear classes 𝒞(0, F ) and we consider a generic configuration of point sources and collocation points as presented in Figure 4, for the case of a circular and a peanut shape domain Ω. In the following simulations we used the collocation and source points presented in Figure 4, and 15 frequencies with . A Tikhonov regularization scheme (the parameter was obtained by the L-curve analysis) is used while solving the ill-conditioned systems.

Figure 4. Distribution of points in two geometries: (a) circle with radius 1, (b) a peanut shape. Note: Domain collocation points z_i (black dots), boundary collocation points x_i (grey dots) and external point sources y_j (bold black dots).

Figure 5. (a) The computed g and (b) The absolute error of the source, in Simulation 1.

•

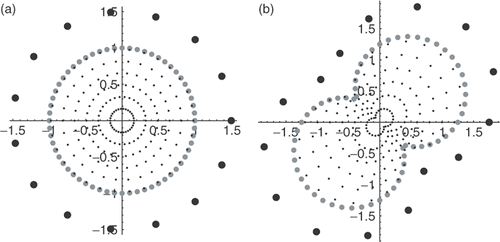
Simulation 1 We considered the unitary circle Ω = B(0, 1) and used 15 uniformly distributed source points on the auxiliary boundary (Figure 4(a), bold dots). On the boundary ∂Ω, we considered 60 uniformly distributed points and on Ω, 180 points. As exact solution, we used the function This leads to the source g(x) = 2ex1 − x2 and we attempt to recover it assuming that g ∈ 𝒞(0, F), with F(x) = 4ex1 − x2. This example was recently considered using a standard MFS method and the class 𝒞(2, 0) in 19. A pointwise relative noise of 2% was then considered. With the same noise level and measuring the flux on 60 equally spaces points on ∂Ω, we plot in Figure 5 the computed solution and the error. In the discrete L2 norm, we obtained a relative error of 1%, which is considerably smaller than 25%, presented in 19.

•

Simulation 2 In a second simulation, we considered Ω to be the peanut shape defined by the non-smooth radial function We used the same amount of source points, boundary and domain collocation points Figure 4(b) as in Simulation 1. The exact solution was This leads to the source g(x) = 4e− 2(x1² + 2x2²)(3 − 4x1² − 16x2²), which is plotted in Figure 6 [note that u verifies Δu(x) = (16(x1² + 4x2²) − 12)u(x)]. In this simulation, the noise was generated using the normal distribution N(0, 0.08) and we considered 60 measurement points. The geometry was not trivial (it has two inner corners) and therefore the reconstruction presented in Figure 6, is to be considered good.

5.2. Nonlinear case – characteristic sources

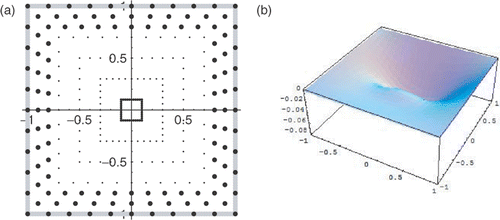
To recover the support ω of a characteristic source, we considered the restriction (37). We took the domain Ω =] −1,1[² and fixed a number of internal points x_p near the boundary where (big black dots in Figure 7(a)), and on the other internal points x_p we apply the restriction (37) as described in the Section 3.4.2 (small black dots in Figure 7a).

•

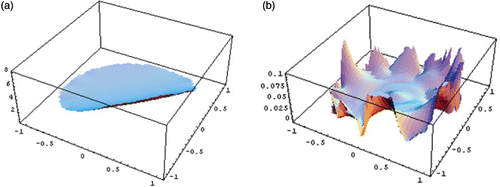
Simulation 3 In this simulation, we consider the recovery of a characteristic function defined by the support set ω1 with parametrized boundary The input temperature T0 was taken to be null, and the 120 measurements Q were considered with 10% random norm noise (using the norm p = ∞). The reconstruction of was made using 48 internal centers for the Bessel J function (with 8 frequencies each), and 24 external source points for the Bilaplacian fundamental solution. This reconstruction is presented in Figure 7(b). Having obtained the source approximation is presented in Figure 8(a). Since the reconstruction of the characteristic function given by is not restricted to 0 or 1 values, this approximation does not have the full restriction known in the problem. Anyhow, it follows the general behaviour, and this can be seen by imposing a binary criteria for the half amplitude. In Figure 8(b) we present a density plot cutted at half amplitude of and compare with the true ω1 (dotted boundary). In Figure 8(b), we see that reconstruction gives a good approximation of the support set ω1.

•

Simulation 4 In the same setting of Simulation 3, we consider the recovery of a characteristic function defined by the support set ω2 with parametrized boundary Again, the input temperature T0 was taken to be null, and the 120 measurements Q were considered with 10% random (norm) noise. The reconstruction of using the same functions, is presented in Figure 9(a). In Figure 9(b) we present the density plot cutted at half amplitude and we see that it follows the true ω2 (dotted boundary). The approximation does not give a good reconstruction of the details but it is quite good in terms of the location and gives a rough approximation of the shape, taking into account the 10% noise level.

Figure 6. Simulation 2: (a) The exact g, and (b) The computed g with noisy data.

Figure 7. Simulation 3: Reconstruction of χ_ω1. (a) The choice of collocation points; (b) the approximation of T.

Figure 8. Simulation 3: Reconstruction of χ_ω1. (a) the approximation of g = χ_ω1; (b) A density plot cutted at half amplitude of and the comparison with ω₁ (dotted boundary).

Figure 9. Simulation 4: Reconstruction of χ_ω2. (a) The approximation ; (b) A density plot cutted at half amplitude of and the comparison with ω₂ (dotted boundary).

6. Conclusions

In this work, we used an extension of the MFS-D to estimate an unknown source term in a linear heat conduction problem, by using only non-intrusive measurements. The uniqueness questions were discussed and some counter examples and criteria for uniqueness were given. The MFS-D showed to be fast and robust to recover general types of sources, which included smooth sources – in some linear class or discontinuous functions defined by characteristic functions.

Acknowledgements

This work results from a cooperation between the Engineering and Mathematics departments of UFRJ and IST. The work was partially funded by CNPq, CAPES (agencies for the fostering of science from the Brazilian Ministry of Science and Education, respectively) and FCT, GRICES (agencies for the fostering of science from the Portugal Ministry of Science and Higher Education) and projects POCI MAT/60863/2004, ECM/58940/2004.