Shape optimization of 3D viscous flow fields

Abstract

This article presents a numerical solution technique for shape optimization problems of steady-state, 3D viscous flow fields. In a previous study, the authors formulated shape optimization problems by considering the minimization of total dissipation energy in the domain of a viscous flow field, proposing a solution technique in which the traction method is applied by making use of a shape gradient. This approach was found to be effective for 2D problems for low Reynolds number flows. In the present study, the validity of the proposed solution technique is confirmed by extending its application to 3D problems.

Keywords:

• shape optimization
• computational fluid dynamics
• shape gradient
• adjoint variable method

1. Introduction

Shape optimization problems, in which the total dissipation energy in a channel used for the transportation of viscous fluid or the drag-power of a moving body in a viscous fluid is minimized, are important engineering problems from the viewpoint of increasing energy efficiency. From a morphological point of view, the solution of these problems provides a basis for understanding the shapes of vascular branches of living things, such as plants and animals.

The theory of shape optimization for incompressible viscous flow fields was initiated by Pironneau 1–3, who formulated a shape optimization problem for an isolated body located in a uniform viscous flow field to minimize the drag-power on this body. The distributed shape sensitivity, which was called the shape gradient, was derived with respect to domain variation by means of an adjoint variable method based on optimal control theory. The adjoint variable method introduces adjoint variables into variational forms of the governing equations as variational variables, and determines the adjoint variables using adjoint equations derived from criteria defining an optimality condition with respect to domain variation. In the viscous flow field problem, the inclusion of the adjoint equations necessitates an analysis of an adjoint fluid velocity and an adjoint pressure, in addition to the governing equations, i.e. the Navier–Stokes equations and the continuity equation for the fluid velocity and pressure.

In subsequent work, Glowinski and Pironneau 4 presented numerical solutions of the minimum-drag profile of a 2D body located in laminar flow using a boundary-layer splicing method, i.e. an inviscid/viscid patching method. Independently of this research group, for many years Jameson 5,6 has also advocated and used control-theory techniques in the aerodynamic design of computational fluid dynamics using a continuous adjoint variable method.

Sano and Sakai 7 and Ganesh 8 analysed 2D shape optimization problems of an isolated body for Stokes flow fields using the numerical procedure proposed by Pironneau 3, in which degrees of freedom of the finite element nodal points on the isolated body's surface are chosen as design variables. They obtained an elliptical shape as the optimal shape. Ganesh 8 analysed a similar problem at a Reynolds number of 20, and obtained an ovoid, whose sharp end was pointed towards the upstream direction of the flow in the optimal shape. Huan and Modi 9,10 analysed similar isolated body problems at a high Reynolds number, solving the original governing equations and adjoint equations using modified boundary conditions. Specifically, they replaced the Dirichlet outflow conditions with less restrictive Neumann outflow conditions.

All the studies introduced above made use of general gradient-based optimizations, such as the steepest descent method, based on the shape sensitivity for the discrete model. These methods, however, present the disadvantage of the large computational calculation time required for optimization processing when the number of the degrees of freedom for the finite element model increases. In addition, the mesh of internal nodes had to be refined in the process of updating the shape.

The present authors have proposed an approach for the optimization of the shape of such channels or bodies based on a gradient method using the distributed shape sensitivity, which we called the shape gradient, with respect to domain variation. In previous studies 11,12, the present authors presented a numerical method for the minimization of the dissipation-energy of steady-state viscous flow fields, and applied this method to 2D problems.

The present study describes the extension of this method for application to the shape optimization of 3D viscous flow fields including convection terms. Reshaping was accomplished using the traction method 13–15, which was proposed as a means of solving boundary-shape optimization problems of domains in which partial differential equations must be solved subject to boundary value conditions. In the traction method, domain variations that minimize the objective functional are obtained as solutions of pseudo-linear elastic problems of continua defined in the design domain. These continua are loaded with pseudo-distributed traction in proportion to the shape gradient in the design domain. Both the evaluation of the shape gradient and the solution of the pseudo-linear elastic problems evaluating the domain variation can be obtained numerically using the finite-element method. Use of this numerical method makes it possible to apply the traction method to complex shape optimization problems with a large number of design variables, as in the case for 3D problems. In addition, since the traction method is implemented by means of the finite-element method, it is exceptionally easy to perform and offers the advantage that it is not necessary to refine the mesh of the internal nodes of the domain. The shape is updated in the traction method by modifying the displacements in the pseudoelastic body loaded with traction in proportion to the shape gradient. Thus, the present technique avoids the distortions that are observed in conventional shape optimization analyses caused by the movement of their internal finite element meshes.

In this article, a dissipation-energy minimization problem for viscous flow fields is considered. Based on the formulation of the shape optimization problem, the governing equations for calculating the shape gradient are derived using the adjoint variable method, the Lagrange multiplier method and the material derivative. Finite-element methods are used to obtain numerical solutions for the viscous flow fields, the adjoint equations and the reshaping by the traction method. Lastly, the validity of this numerical method is confirmed by application to several fundamental 3D problems.

2. Domain variation

Before formulating the shape optimization problem, we first briefly discuss a method of representing domain variation using the speed method. A more detailed explanation of this technique is given in 16.

Consider a domain Ω ⊂ Rⁿ, where n = 2 or 3 and R is the set of real numbers. The boundary of Ω, Γ, is variable. One approach to describe the domain variation is to use a one-parameter family of one-to-one mappings T_s(X) : Ω ∋ X ↦ x ∈ Ω_s, where s denotes the domain variation history.

Consider a domain functional J_Ω of a distributed function φ. Denoting the derivative of such a functional with respect to s by , then the value of this derivative at s = 0 is given by the material derivative: (1) where ν is an outward unit normal vector on the boundary. The shape derivative, φ′, of the distributed function φ denotes the derivative of this function under a spatially fixed condition. The derivative of T_s(X) with respect to s is given by (2) and is called the velocity due to the analogy between s and time.

3. Minimization of the total dissipation energy of a viscous flow field

Let us consider a steady-state viscous flow field of an incompressible Newtonian fluid in domain Ω ⊂ Rⁿ with boundary Γ = Γ₀ ∪ Γ_w ∪ Γ₁. Let fluid velocity be bounded with a prescribed fluid velocity û ∈ (H^1/2(Γ₀))ⁿ on an inhomogeneous Dirichlet-type sub-boundary Γ₀, and let u = 0 on a homogeneous Dirichlet-type sub-boundary Γ_w: (3) and satisfy the boundary condition (4) with a prescribed force on a Neumann-type sub-boundary Γ₁. Let pressure p ∈ Q where (5) The density ρ ∈ L^∞(Ω) and co-efficent of viscosity μ ∈ L^∞(Ω) are assumed to be given.

3.1. Formulation of problem

The total dissipation energy minimization problem under volume constraint M > 0 is formulated as: (6) (7) (8) (9) (10) (11) where Equations (9) and (10) are variational forms, or weak forms, using the adjoint velocity , where (12) and the adjoint pressure q ∈ Q for the governing equations, i.e. the Navier–Stokes equations and the continuity equation. Equation (11) describes the volume constraint. The viscous term a^V(u, w), the convective term b(v, u, w), the pressure term c(w, p), and the stress term d(w) are defined by (13) (14) (15) (16) where . The Einstein summation convention and partial differential notation (·)_,i = ∂(·)/∂x_i are used in the tensor notation of this article.

3.2. Shape gradient

Applying the Lagrange multiplier and adjoint variable methods, this problem can be transformed into a stationary problem of the Lagrange functional L(u, p, w, q), (17) where w ∈ W and q ∈ Q are the adjoint variables with respect to the fluid velocity and the pressure, respectively. The non-negative real number Λ is the Lagrange multiplier with respect to the volume constraint.

Imposing the condition that the inhomogeneous Dirichlet-type sub-boundary Γ₀ and the Neumann-type sub-boundary Γ₁ are invariable under reshaping allows the derivative of L with respect to s, , to be simply expressed as: (18) where is the material derivative, and (·)′ is the shape derivative for the domain variation of the distributed function under a spatially fixed condition. The linear form ⟨ Gν, V ⟩ with respect to the velocity function V is given by (19) (20) (21)

Considering stationary conditions for the variables w′ ∈ W, q′ ∈ Q, u′ ∈ W and p′ ∈ Q appearing in Equation (18), the Kuhn–Tucker conditions with respect to u, p, w, q are obtained as (22) (23) (24) (25) (26) with Equations (22–25) describing variational forms of the original governing equations for fluid velocity u and pressure p, and variational forms of the adjoint equations for adjoint velocity w, and adjoint pressure q, which we call adjoint equations. If Equations (22–26) are satisfied, the derivative of the Lagrange functional agrees with that of the objective functional and the linear form ⟨ Gν, V ⟩ with respect to the velocity function V: (27) The coefficent vector Gν in Equation (19) represents the sensitivity of the velocity function to domain variation, and is called the shape gradient. The scalar function G is called the shape gradient density.

4. Numerical solution technique

4.1. Traction method

If the shape gradient is obtained, the traction method 13–15 can be applied to optimize the geometrical domain shape. The traction method has been proposed as a procedure for solving the velocity V ∈ D by (28) where a^E(·, ·) is defined by (29) and where {A_ijkl}_{i, j,k,l=1,2, …, n}, and denote an elastic tensor, displacement and variational displacements, respectively. Equation (28) indicates that the velocity V decreasing in the objective functional, that is the dissipation energy in this study, is obtained as a displacement of a pseudo-elastic body defined in Ω by the loading of a pseudo-external force in proportion to −Gν, under constraints on the displacement of invariable boundaries. The robustness of the traction method to oscillating phenomena, which often occur at the moving boundary nodes of finite-element models in proportion to the negative value of the shape gradient, has been confirmed theoretically 14.

4.2. Numerical procedure

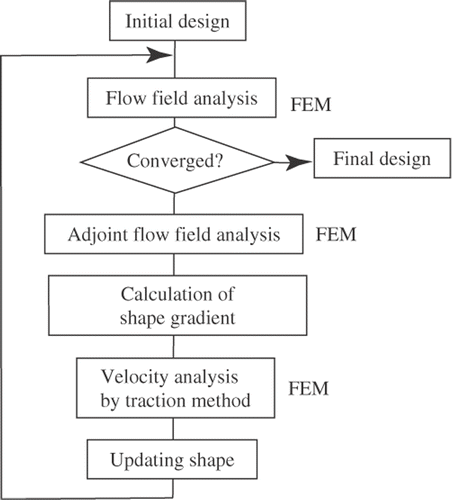
A flow chart of the shape optimization system is shown in Figure 1. Finite-element methods were employed in all the analysis steps of the system. Shape optimization analysis was performed by executing these elements sequentially and repeatedly.

Figure 1. Flow chart of shape optimization procedure.

The shape gradient was evaluated using the two viscous flow-field analyses, which obtain distributions of fluid velocity u, pressure p solving the non-linear original governing Equations (22) and (23), and the distributions of adjoint fluid velocity w, and adjoint pressure q solving the linear adjoint Equations (24) and (25). For the case of 3D problems considered in this study, we used the Taylor–Hood elements in the finite-element analysis. That is, the complete polynomial series to the second-order terms was used to provide interpolation functions for u and w, while the linear polynomial series was used to provide interpolation functions for p and q. Further, a tetrahedral finite-element with 10 nodes for u and w and four nodes for p and q was also employed. The non-linear original governing Equations (22) and (23) were solved by the Newton–Raphson method.

The shape gradient was calculated using the results of these analyses. The domain variation V in Equation (28) was analysed using the finite-element method, using second-order finite-elements for V. The Lagrange multiplier Λ, determined so as to satisfy the volume constraint, can be regarded as a uniform surface force in the external force −Gν. Therefore, it should be possible to satisfy the conditions of Equation (26) by controlling the magnitude of this uniform surface force, Λ.

5. Numerical results

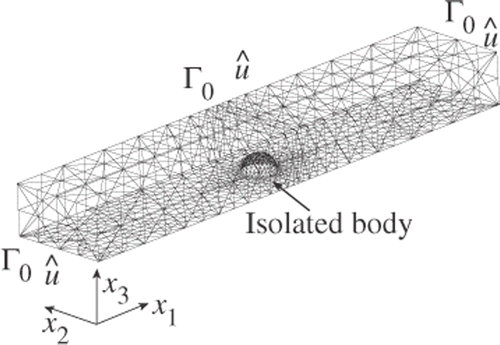
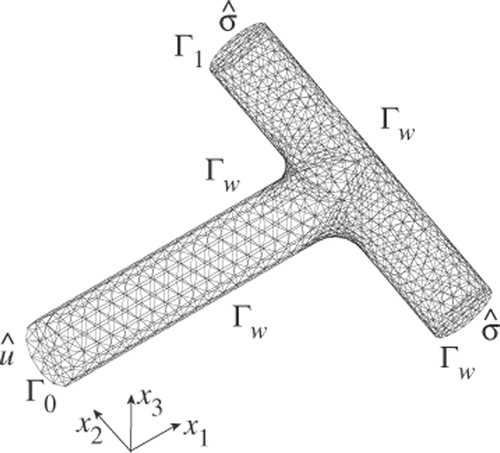
We present numerical results for two 3D low Reynolds number viscous flow problems: for an isolated body in uniform flow, and for a branch channel, as shown in Figures 2 and 3, respectively.

Figure 2. 3D isolated body problem and finite-element meshes.

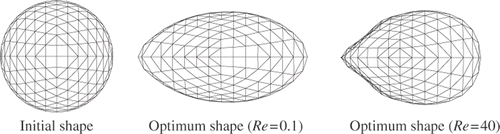
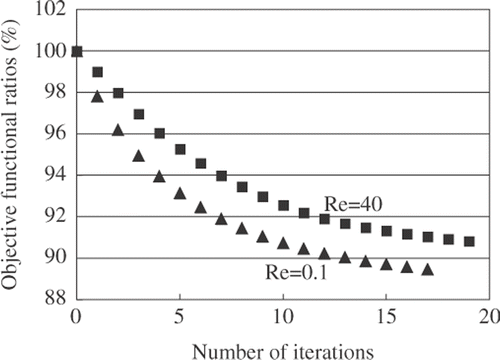
The FEM model and boundary conditions for the isolated body problem are shown in Figure 2, where the design boundary was designated to be the surface boundary Γ_w of the isolated body. The Reynolds number is defined from the magnitude of the uniform flow û and the initial diameter of the isolated body. Symmetry about the channel centre-plane was also exploited for this problem, and the total numbers of nodes and elements are 10,681 and 6,484, respectively. Figures 4 and 5 illustrate the results of the isolated body problem. On the basis of these results, we can observe that the optimal shape is ellipsoidal at Re = 0.1 (Stokes flow) and ovoid at Re = 40, where the sharp end points to the upstream direction of the flow. The numerical results for Stokes flow are in good agreement with the shape considered by Pironneau 1. The monotonic convergences of the iteration histories of dissipation energy in both problems confirm the validity of the proposed method.

Figure 3. 3D branch channel problem and finite-element meshes.

Figure 4. Numerical results for isolated body problem, initial shape and optimum shapes.

Figure 5. Numerical results for isolated body problem, iterative histories.

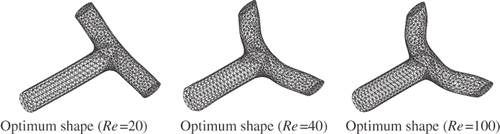
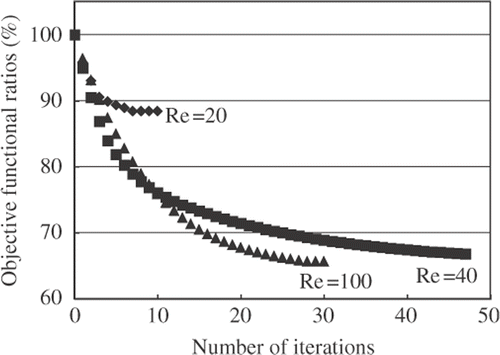
Regarding the configuration of the branch channel problem shown in Figure 3, fluid flows in from a boundary Γ₀ and flows out from two boundaries Γ₁. Poiseuille flow û was assumed at the entrance boundary Γ₀, and a prescribed force was assumed at the exit boundaries Γ₁. The design boundary is given by the whole of the wall boundary Γ_w. The entrance boundary Γ₀ and the exit boundaries Γ₁ were restricted for the reshaping. The Reynolds number is defined from the mean of the Poiseuille flow û and the width at the entrance boundary Γ₀. The total numbers of nodes and elements are 9229 and 5052, respectively. The numerical results of this problem at Re = 20, 40 and 100 are shown in Figures 6 and 7.

Figure 6. Numerical results for branch channel problem, optimum shapes.

Figure 7. Numerical results for branch channel problem, iterative histories.

The values of the objective functional in both problems were converged, and thus we confirmed the validity of the present method.

6. Conclusions

In this article, we formulated a dissipation-energy minimization problem for steady-state viscous flow fields, and derived the shape gradient with respect to this problem. The validity of the traction method using the derived shape gradient was confirmed on the basis of the numerical results obtained by applying the method to two 3D shape optimization problems.

Acknowledgements

This study was financially supported by The Koshiyama Research Grant in Japan. We express our gratitude to Mr Naoshi Nishihashi, student of the Gifu National College of Technology, for his cooperation.