Abstract
The boundary element method and the techniques of parameter estimation are coupled to identify the internal structure of an inhomogeneous body using a discrete number of surface measurements. In this study, a body of some arbitrary but given shape is subjected to uniaxial tension. The body is assumed to contain an inclusion of circular shape but of unknown location, size, Poisson's ratio and shear modulus. The simultaneous estimation of these parameters is to be accomplished by measuring displacements at surface locations where tractions have been specified and/or measuring tractions at selected surface locations where displacement has been specified. The parameter estimation technique with line search is used for optimization.
1. Introduction
Material characterization is one of the fundamental tasks of engineering and science. It involves the study of inverse problems that usually imply identification of inputs from outputs. In this study, the feasibility of characterizing the internal structure of an inhomogeneous body using a discrete number of surface measurements is explored. In particular, we examine the problem of determining the location, size and mechanical properties of an inclusion in a body of arbitrary shape. The boundary element method, Brebbia and Dominguez Citation1, is adapted for application to this parameter estimation, Beck and Arnold Citation2, problem. This study is an extension of previous investigations that involved inverse steady-state heat transfer problem, Khodadad-Saryazdi and Altiero Citation3 estimated the thermal conductivity, location and radius of one circular inclusion and Khodadad-Saryazdi et al. Citation4 estimated the thermal conductivity, location and radius of two circular inclusions inside a solid body.
Other numerical techniques, most notably finite differences and finite elements, have been used to investigate various types of inverse problems. Schnur and Zabaras Citation5 use finite element solution of two-dimensional inverse elastic problems using spatial smoothing to calculate the surface tractions on a body from internal measurements of displacement at discrete sensor locations. The same authors Citation6 also investigate an inverse method for detecting elastic material properties and material interface using finite element analysis for solving a two-dimensional inverse parameter estimation problem in solid mechanics.
However, for the non-linear inverse problem investigated here, an iterative scheme is required. Thus the boundary element method, which requires only the discretization of the boundary, must be employed in order to avoid the costly and unnecessary task of grid generation for the entire multiply connected domain at each iteration.
Application of the boundary element method to the inverse problem of material characterization is not entirely new. Murai and Kagawa Citation7 investigated the estimation of the shape of an inclusion in a two-dimensional region using impedance measurements on the domain surface. The boundary element method was used in conjunction with a simple linearized estimation scheme.
Ohnaka and Uosaki Citation8 utilized surface temperature measurements to simultaneously estimate the diffusion constant of an homogeneous body as well as discrete unknown internal heat sources. It was revealed that the accuracy of the identification results is lower when the actual heat source is located close to the boundary.
Dulikravich Citation9 investigated the optimal size and location of coolant flow passages for a user-specified steady distribution of surface temperatures and heat fluxes. An error function was then used in a constrained optimization routine to determine the new updated size and location of the coolant flow passages so that the difference between the desired and the computed surface heat fluxes and/or temperatures was minimized.
Gao and Mura Citation10, utilized surface displacement data to evaluate the residual stress field in the vicinity of a damaged region caused by a series of unknown loading.
Das and Mitra Citation11, found the location and size of a flaw using measured surface temperatures. An algorithm for the detection of the flaw was employed.
Kassab et al. Citation12 investigated the non-destructive detection of cavities by an inverse elastostatics boundary element method. The boundary element method coupled with Newton's method and the steepest descent methods are considered for the detection of single circular and elliptic holes located at various positions within a rectangular plate.
In some latest researches, characterization of the internal structure of an inhomogeneous body is considered. Lee and Park Citation13 tried to identify the geometric shape and material properties of inclusions in two-dimensional finite bodies.
Alessandrini et al. Citation14 considered the problem of determining an inclusion in an elastic isotropic body. They proved that the volume of the inclusion can be estimated only depending on the boundary traction and displacement.
With regard to the ill-posed nature of the inverse problems, the estimation process is very sensitive to the errors involved in experimental measurements. To correct this problem, several regularization functions are employed by Lee et al. Citation13,Citation15. Although each of these methods have some advantages, none of them are completely effective.
Khodadad and Dashti-Ardakani Citation16 investigated the shape estimation problem to identify an inclusion of arbitrary shape located inside a solid body using genetic algorithm and the conjugate gradient method. The boundary elements method is adapted in this inverse elasticity problem.
Huang and Chao Citation17 in an inverse geometry problem, conclude that the techniques of function estimation would be much better than parameter estimation since the number of unknown parameters is unlimited. When the numbers of unknown parameters are few such as in the case of estimating the mechanical or thermal properties of inclusions, the techniques of parameter estimation are more effective since they certainly converge to the correct solution faster.
The results of the above study are verified by Khodadad and Mazidy Citation18, who employ the parameter estimation method along with regularization function to estimate simultaneously both the shape and mechanical properties of an inclusion located inside a solid body, but their attempt failed. Then only estimation of the shape of an inclusion with known mechanical properties is attempted and only 35% of the cases converge to the correct solution. It is also observed that implementation of the regularization function is not effective in inverse elasticity problems when the initial guess of the unknown parameters is not very good.
The present investigation assumes a two-dimensional body containing a single inclusion, but the method of analysis is not limited in principle. Extension to three-dimensional problems and more complex internal structure is straightforward but the additional question of how many parameters one can hope to determine simultaneously by employing different optimization methods such as the global optimization methods requires further study. Nonetheless, the success of the technique demonstrated here shows great promise for application in the area of non-destructive evaluation.
2. Boundary element method
A linear elastic solid of uniform thickness h, loaded in some manner, is considered. The equations of equilibrium in terms of displacements are
(1)
For an isotropic material
(2)
where, G is shear modulus and
and ν is Poisson's ratio. The boundary conditions are
(3)
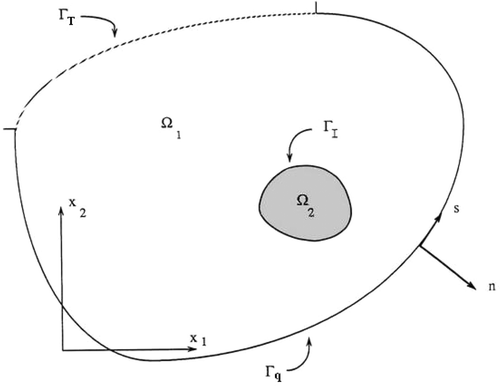
for i = 1, 2, where, ui is the component of displacement in the i direction, ti is the component of traction in the i direction, s is a coordinate along the boundary as shown in , and
and
are prescribed functions.
Note that
(4)
where, n1 and n2 are the components of the outward-directed unit normal to the boundary Γ. The displacement at any point xi in Ω can be determined from Citation1 as
(5)
where, j = 1, 2, k = 1, 2, summation on k is implied, and
(6)
and
(7)
where,
(8)
Application of Equation (5) requires complete knowledge of boundary information, i.e. uk and tk, k = 1, 2, must be known everywhere on Γ. To accomplish this, one may use
(9)
where,
and
if the boundary is smooth at xi, and δkj is the Kronecker delta.
Subdividing the boundary Γ into N segments, Equation (9) becomes
(10)
To employ linear elements we introduce the following quantities on element r
(11)
where, φ1 = (1 − ξ)/2 and φ2 = (1 + ξ)/2 are linear shape functions and
. Note that the displacements are assumed to be piecewise linear and continuous whereas tractions are assumed to be piecewise linear and discontinuous. Equation (10) can now be written in the form
(12)
where,
is taken to be
and
and
are known functions. Equation (12) is written in matrix form as
(13)
where, [H ] has dimension 2N × 2N, and [G ] has dimension 2N × 4N. The column matrix
contains the values of displacements in the x1 and x2 directions at the N boundary nodes and column matrix
contains four values of tractions at each boundary node, i.e. the values of tractions in the x1 and x2 directions ‘before’ the node and the values of tractions in the x1 and x2 directions ‘after’ the node.
For an inhomogeneous body, the domain Ω is divided into two subdomains Ω1 and Ω2, each having its own Poisson's ratio and shear modulus and Equation (13) is applied to each subdomain. For two subdomains
or
(14)
Equation (14) is then reduced by imposition of interface conditions on Γ1, the interface of the two subdomains. At a point i on Γ1
(15)
where, continuity of tractions at the interface nodes is assumed. Implementation of (15) gives us
(16)
where, the subscript ‘I ’ denotes the interface boundary and the subscript ‘1 − I ’ denotes the outer boundary. The matrix
is
and
is
, where N1 is the number of outer boundary nodes and N2 is the number of interface boundary nodes. Equation (16) can be written as
(17)
where, the matrix
is
and
is
.
Equation (17) is reordered based on known outer boundary conditions i.e. all the known outer boundary displacements in are taken to the right-hand side and all unknown boundary tractions in
to the left-hand side, so that:
(18)
which is solved for
, which contains the values of unknown displacements and tractions at the outer boundary nodes as well as all displacements and tractions at the interface boundary nodes.
3. Inverse problem and parameter estimation
In the previous section, the use of the boundary element method to solve the direct linear elasticity problem for homogeneous and inhomogeneous bodies was demonstrated. In the direct problem, the governing equation, geometry, material properties and the boundary conditions are given and the unknown boundary data is computed. In the inverse problem some of the geometric features and/or material properties are unknown, but some of the unknown boundary data can be measured and used as additional information necessary to estimate the unknown input parameters.
In this section, a body that is known to contain a circular inclusion but its location, size and mechanical properties are unknown is considered. We wish to determine these unknown parameters by using the measurements of displacements on the portion of the boundary where tractions are prescribed and/or tractions on the portion of the boundary where displacements are prescribed.
Let us introduce the following column matrices:
| = | = a column matrix containing m measured boundary displacements. | |
| = | = a column matrix containing the same m boundary displacements, computed using the boundary element method. | |
| = | = a column matrix containing n measured tractions. | |
| = | = a column matrix containing the same n tractions, computed using the boundary element method, and |
The fitness function that is the sum of the squared differences between measured and computed displacements and tractions is
(19)
where, the superscript T indicates the transpose of the matrix, and
and
are functions of
. In order to find the best estimate of the unknown parameters, function Z is minimized by setting its derivative with respect to
equal to zero.
The matrix derivative of Z with respect to is
(20)
where
is the matrix derivative operator
Let us define
(21)
where,
, which is m × 5, and
, which is n × 5, are functions of
, and are called sensitivity matrices, also m is the number of boundary measured displacements and n is the number of boundary measured tractions. The ‘ij’ components of the sensitivity matrices are called the sensitivity coefficients.
contains the sensitivities of displacements with respect to
and
contains the sensitivities of tractions with respect to
. In linear estimation problems, sensitivity coefficients are computed in order to predict the best locations on the boundary to conduct measurements. Since in this inverse elasticity problem the displacements and tractions are non-linear functions of
, therefore the sensitivity coefficients are also non-linear functions of
and do not provide effective information about the estimation process Citation19. Inserting Equation (21) into Equation (20) and setting
, yields
(22)
which gives the value of
at which Z is minimized. Note that Equation (22) is non-linear in
. Therefore, the first two terms of the Taylor series in matrix form for
and
about
are used, where
is an estimate of
, and approximate
and
as functions of
, i.e.
(23)
(24)
Substituting Equations (23) and (24) into Equation (22), yields
(25)
Note that now Equation (25) is linear in
.
To indicate an iterative procedure we let
and obtain five equations for five parameters, i.e.
(26)
where,
and M is the iteration number. Since the parameter estimation is a local optimization method, it usually happens that the estimation gets stuck in local optima and after a number of iterations, the fitness function indicated by Equation (19) may never converge to a small value and it could not be a good stopping criterion. Therefore, the follow stopping criteria is used
(27)
where, δ and δ1 are small numbers. Here, following Beck and Arnold Citation2, δ is set equal to 10− 4, and δ1 = 10− 10.
A computer program has been developed which employs the boundary element method as a subroutine. A first guess of the unknown parameters is made and the boundary element subroutine is called to compute the boundary data corresponding to the guessed parameters. Then, using the parameter estimation technique, the computed data at selected locations are compared with their measured values taken at the same locations, and ‘corrected’ values of the parameters are found. The iterations continue until the criteria indicated in Equation (27) is satisfied.
4. Results and discussion
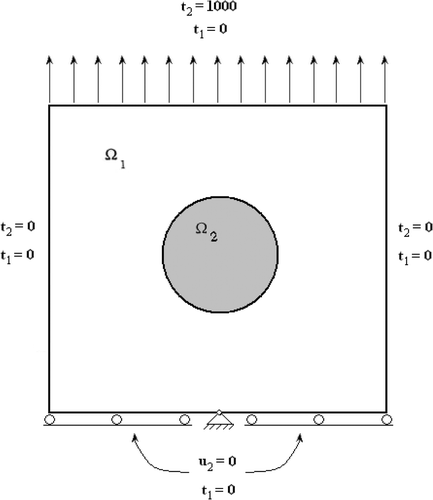
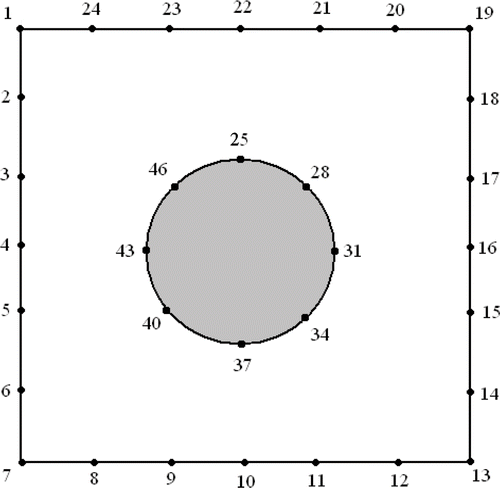
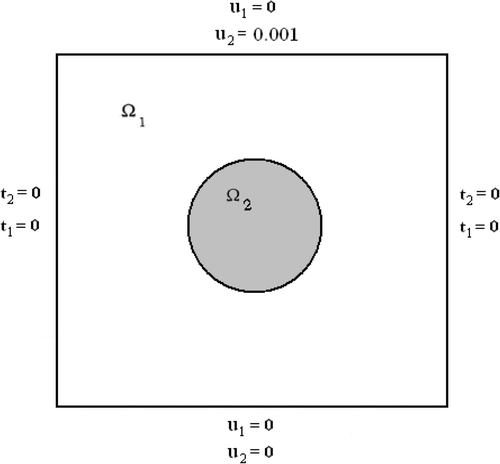
Consider the problem shown in , and where a rectangular body of dimensions (6 m × 6 m) with a circular inclusion of radius 2 located at (3,3) is subjected to the boundary conditions shown in each figure. The shear modulus and Poisson's ratio of the matrix material are 3.0 × 106 and 0.3, respectively, and those of the inclusion are 1.0 × 106 and 0.2. The outer boundary and the interface boundary are each divided into 24 linear elements of equal length as shown in .
The location, radius, shear modulus and Poisson's ratio of the circular inclusion are to be estimated simultaneously using the displacements measured on the portion of the boundary where the traction is specified and/or the traction measured on the portion of the boundary where displacement is specified.
The ‘experiment’ is simulated as follows. The body is analysed by the boundary element method using the exact values of the five parameters and the unknown boundary displacements and tractions are computed. These computed values are then used as the ‘experimental’ results.
The first question addressed is the influence of the initial guessed values of the unknown parameters on convergence. The first attempt was to estimate all five parameters, but it failed. Next, the estimation of four parameters was attempted and it was observed that estimation of any combination of four out of five parameters is possible. Therefore, the radius of the circular inclusion is assumed to be known and the other parameters are estimated as follows. A total of 40 sets of initial guesses were examined and ‘experimental values’ at all the boundary nodal locations were used. Convergence was defined in accordance with Equation (27).
The first problem investigated is shown in . Estimation of the location i.e. x , y coordinate of the centre, shear modulus and Poisson's ratio of the circular inclusion with known size, using all measured displacements in the x1 and x2 directions and tractions in the x1 and x2 directions is attempted, 15.0% of the cases considered converged and 85% of the cases diverged. The reason for the divergence becomes apparent after three or four iterations and can be classified into one of the three following groups: (1) the determinant of for an iteration is zero; (2) the estimated values of
for an iteration are unrealistic, i.e. the estimated inclusion does not lie entirely within the matrix domain; (3) the estimated value of the inclusion Poisson's ratio for an iteration is less than zero or more than 0.5. All of the above three groups are identified during the estimation process and the program will stop if any of the above situations occur. For the above problem, 40.0% of the total cases diverged due to (1), 27.5% of the cases diverged due to (2) and 17.5% of the cases diverged due to (3). The number of iterations ranged from 8 to 15. The same problem was investigated using only the displacement measurements at all nodal locations where tractions were specified, 67.5% of the cases converged, 27.5% of the cases diverged due to (1), and 5.0% of the cases diverged due to (2). The number of iterations ranged from 5 to 20.
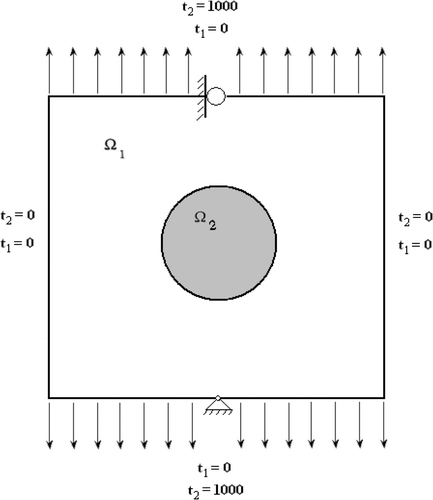
As a result of this observation, another problem with fewer displacement boundary conditions, shown in , was examined. Eighteen displacements in the x1 directions and 18 displacements in the x2 directions were used, 90.0% of the cases converged, 2.5% of the cases diverged due to (1) and 7.5% of the cases diverged due to (3). The number of iterations ranged from 5 to 18.
A third problem, shown in , with an equal number of displacement boundary conditions and traction boundary conditions, was investigated. All the cases involving different initial guesses of the unknown parameters diverged. It is concluded that if the body under investigation has more specified traction boundary conditions, the estimation of the unknown parameters is more successful.
Since the second problem, shown in , resulted in the best convergence, it is used to investigate the remaining issues, from the 40 sets of initial guess tried, the case of G2 = 1.200 × 106,ν2 = 0.300,(xc,yc) = (2.50,2.50) resulted in the most rapid convergence, and is used in addressing all of the following issues.
The second question addressed is the number and combination of surface displacements required to simultaneously estimate the four unknown parameters, i.e. shear modulus, Poisson's ratio and coordinates of the centre of the inclusion. The minimum number of measurements needed to estimate the above four parameters was found to be 20. We considered five different combinations of 10 displacements in the x1 direction and 10 displacements in the x2 direction, only one case converged.
Estimation of only two parameters, i.e. shear modulus and Poisson's ratio of the circular inclusion with known location and size is investigated next. Results show that by selecting the right locations on the surface of the boundary, it is possible to estimate the above two parameters successfully by measuring only eight displacements. This requires analysing the plots of the sensitivity coefficients, for more details of this analysis reference Citation19 is suggested. Results show that even with 18 displacement measurements, if the locations are not selected carefully, the estimation will diverge. Estimation of G2 and ν2 using less than eight measurements was not successful.
The final question addressed is the effect of errors in the experimental measurements on the ability to estimate the sought parameters. The experimental measurements with errors are achieved by simulating the ‘experiment’ as follows. The body is first analyzed by the boundary element method using the exact values of the four parameters. Then random errors are added to the computed boundary displacements, and these are taken to be the ‘measured’ data. The statistical assumptions regarding the introduced errors are additive, non-correlated, normally distributed and have zero mean and constant variance. These errors are generated following a procedure discussed in Beck and Arnold Citation2. shows the results when 18 displacements in the x1 direction and 18 displacements in the x2 direction, with different percent errors were used to estimate the four unknown parameters. It is observed that as the mean percent error increases, the number of iterations also increases, but it is possible to estimate the unknown parameters with experimental errors as high as 4.0%. All the results in are rounded off to three significant figures.
Table 1. Influence of experimental errors on the estimation.
5. Conclusions and recommendations
A technique has been proposed which couples the boundary element and parameter estimation methods for the purpose of characterizing the interior of an inhomogeneous body utilizing surface measurements only. The parameter estimation technique presented here addressed several questions that arose regarding implementation of this technique to elasticity problems. Although the technique does not always converge, the cases that do converge give excellent results. Also, the method never converges to an incorrect solution. Based on the results of this investigation, the following conclusions are drawn:
| 1. | Better results are obtained for elasticity problems when more displacement measurements are used. | ||||
| 2. | More success is achieved in estimating only the shear modulus and Poisson's ratio of the inclusion than in estimating these material properties along with the geometric parameters. | ||||
| 3. | It is observed that as the number of unknown parameters increases, the ability of the parameter estimation technique decreases. Also to have convergence in the solution, a very good initial guess is required. | ||||
Acknowledgements
The authors would like to acknowledge the financial support received from the Research Council of Yazd University.
References
- Brebbia, CA, and Dominguez, J, 1989. Boundary Elements: An Introductory Course. Southampton: Computational Mechanics Publications; 1989.
- Beck, JV, and Arnold, KJ, 1977. Parameter Estimation in Engineering and Science. New York: John Wiley and Sons; 1977.
- Khodadad-Saryazdi, M, and Altiero, NJ, 1990. Characterization of the interior of an inhomogeneous body using surface temperature and/or heat flux measurements. East Lansing, Michigan, USA: Third Annual Inverse Problems in Engineering Seminar; 1990.
- Khodadad-Saryazdi, M, Seyed-Rihani, SA, and Abbasiyan, M, 2002. "Estimation of the parameters related to impurities inside solid bodies using the inverse and boundary element methods". In: 10th Annual (International) Conferences of Mechanical Engineering, ISME2002. Tehran, Iran: Khajeh Nasir Toosi University; 2002.
- Schnur, DS, and Zabaras, N, 1990. Finite element solution of two-dimensional inverse elastic problems using spatial smoothing, Int. J. Numer. Meth. Engng. 30 (1990), pp. 57–75.
- Schnur, DS, and Zabaras, N, 1992. An inverse method for determining elastic material properties and material interface, Int. J. Numer. Meth. Engng. 33 (1992), pp. 2039–2057.
- Murai, T, and Kagawa, Y, 1986. Boundary element iterative techniques for determining the interface boundary between two Laplace domains: a basic study of impedance plethysmography as an inverse problem, Int. J. Numer. Meth. Engng. 23 (1986), pp. 35–47.
- Ohnaka, K, and Uosaki, K, 1987. Simultaneous identification of the external input and parameters of diffusion type distributed parameter systems, Int. J. Control. 46 (3) (1987), pp. 889–895.
- Dulicravich, GS, 1988. Inverse design and active control concepts in strong unsteady heat conduction, Appl. Mech. Rev. 41 (6) (1988), pp. 270–277.
- Gao, Z, and Mura, T, 1989. On the inversion of residual stresses from surface displacements, J. Appl. Mech. 56 (1989), pp. 508–513.
- Das, S, and Mitra, AK, 1989. An algorithm for the solution of inverse Laplace problems using BEM, Developments in Mechanics 15 (1989), pp. 525–526.
- Kassab, AJ, Moslehy, FA, and Daryapurkar, AB, 1994. Nondestructive detection of cavities by an inverse elastostatics boundary element method, Engng. Anal. Bound. Elem. 13 (1994), pp. 4–555.
- Lee, HS, Park, CHJ, and Park, HW, 2000. Identification of geometric shapes and material properties of inclusions in two-dimensional finite bodies by boundary parameterization, Comput. Mechods Appl. Mech. Eng. 181 (2000), pp. 1–20.
- Alessandrini, G, Morassi, A, and Rosset, E, 2002. Detecting an inclusion in an elastic body by boundary measurement, SIAM J. Math. Anal. 33 (6) (2002), pp. 1247–1268.
- Lee, HS, Kim, YH, Park, CHJ, and Park, HW, 1999. A new spatial regularization scheme for the identification of geometric shape of an inclusions in finite body, Int. J. Numer. Meth. Eng. 46 (7) (1999), pp. 973–992.
- Khodadad, M, and Dashti-Ardakani, M, 2008. Inclusion Identification by inverse application of boundary element method, Genetic Algorithm and Conjugate Gradient Method, Am. J. Applied Sci. 5 (9) (2008), pp. 1158–1166.
- Huang, CH, and Chao, BH, 1997. An inverse geometry problem in identifying irregular boundary configurations, Int. J. Heat Mass Transfer. 40 (1997), pp. 2045–2053.
- Khodadad, M, and Mazidy, A, 2005. "Estimation of the shape and location of an inclusion inside an elastic two-dimensional body using inverse method". In: 13th Annual (International) Conferences of Mechanical Engineering, ISME2005. Isfahan, Iran: Isfahan University of Technology; 2005.
- Khodadad-Saryazdi, M, 1990. "Characterization of the interior of an inhomogeneous body using surface measurements". In: Ph.D. thesis. East Lancing, Michigan, USA: Michigan State University; 1990.