Ocean current prediction in towed cable hydrodynamics under dynamic steering

Abstract

This article considers the problem of reconstructing the velocities of ocean currents impinging on a towed streamer cable sparsely equipped with steering elements (SE). The study is based on a two-dimensional model describing the quasi-steady motion of the towed cable in the presence of hydrodynamic drag and steering forces that depend nonlinearly on the angle of attack. To derive the proposed methodology we first outline the hydrodynamic equations used in solving the forward problem by which the cable's velocity, curvature and tension are obtained in the knowledge of the towing vessel's motion, the ocean current velocities and the drag coefficient characteristics of the SE. In sequence, we formulate the inverse problem of inferring the ocean velocities using a finite set of noise-infused positioning and tension measurements showing that this is nonlinear and ill-posed. To solve the inverse problem we adopt Newton's scheme for nonlinear convex problems in conjunction with generalized Tikhonov regularization. The problem under consideration bares significant differences from the linear non-steered formulation addressed in (N. Polydorides, E. Storteig and W. Lionheart, 2007, Forward and inverse problems in towed cable hydrodynamics, Ocean Engineering 35 (2008)), due to the nonlinearity in the forward method as well as the discontinuities observed in the forward measurements due to the steering forces. A series of numerical simulation studies is subsequently presented in order to demonstrate the practical performance of the proposed technique in reconstructing the ocean currents velocity profile and angle of attack.

Keywords:

• cable hydrodynamics
• steering elements
• angle of attack
• nonlinear ill-posed problem

1. Introduction and motivation

Offshore seismic data acquisition relies on acoustic sensors mounted on long flexible cables, also known as streamers, towed in the sea by appropriately equipped vessels. An important aspect in exploring oilfield reservoirs lies with the quality and repeatability of the measurements, which in turn requires fully calibrated and accurately positioned sources and receivers. Although the vessel's trajectory is easily traced, that of the streamer is far more challenging, mainly due to the impact of the varying physical conditions. The effective positioning of the acoustic sensors mounted on the cable at their target positions is realistically feasible only through optimal steering, performed by specially designed steering deflectors sparsely populated along its length. In realistic conditions, variable sea currents compromise the exact positioning of hydrophones and air guns, with immediate effects on the accuracy and repeatability of seismic data. If the ocean current velocities can be retrieved in real time, then the algorithms controlling the steering can be optimized. This work is aimed in deriving a methodology for inferring in real time the ocean current velocity profiles (OCVP) impinging on a towed streamer cable under seismic survey.

In this context, we propose a robust method for reconstructing the ocean currents at small regular time intervals thereby allowing for optimal steering and improvement in the quality of the acquired data. The technique addresses the problem in the framework of inverse problem theory, where one seeks to recover the OCVP along the streamer when noisy positioning and tension measurements are available. In simple terms the goal is to identify the ocean currents that yield the observed cable shape, provided that such a profile realistically exists and can be uniquely determined from a set of finite approximate data.

The inclusion of steering elements (SE) inevitably alters the homogeneity of the problem as indeed the physical characteristics of the steamer cable. In response, the model is appropriately modified from its basic configuration as posed by Dowling 1 to accommodate the additional drag forces exerted on SE. As these are equipped with flexible wings, their corresponding drag forces vary dynamically with respect to the angle by which the ocean currents ‘attack’ the cable. Numerical and experimental work have demonstrated that the drag forces relate nonlinearly to the angles of attack and consequently the ocean currents at any given instant 2. From a computational prospective the augmented forward equations remain suitable for numerical treatment as in 3 and 4, however the inverse problem becomes more challenging as the extra forces involve the required ocean currents in nonlinear form. Evidently, the introduction of SE essentially transforms the inverse problem from quasi-linear and mildly ill-posed to nonlinear ill-posed, distorting at the same time the otherwise smooth curvature of the cable with severe consequences on the differentiability of the forward data. The variant problem formulation, which requires the recovery of the OCVP without any steering is linear and the forward variables (signals) are continuous in space, allowing the implementation of smooth inversion methods as this has been addressed in 5.

In order to allow for a rigorous presentation of the method, this article is organized as follows: In the next section, we present the forward model describing the quasi-steady motion of the cable in the influence of hydrodynamic loads, and then analyse the impact of SE on the characteristics of the forward measurements. In sequence, we formulate the nonlinear inverse problem by recasting the forward model in a Tikhonov regularized integral formulation that enhances stability in the presence of noise perturbations in the forward parameters. The resulting nonlinear residual equations are subsequently non-dimensionalized (NDM) before being addressed simultaneously in the context of Newton's method. Some numerical results are presented to demonstrate the performance of the method in reconstructing the ocean current profiles and predicting the angle of attack.

2. Towed cable hydrodynamics with dynamic steering

2.1. The forward model

The motion of inextensible cables towed in incompressible fluids can be approximated in terms of the hydrodynamic model 6 (1) These equations are derived from Newton's second law and refer to the distribution of forces exerted on a cable positioned in an orthogonal coordinate frame (t, n, b). The cable's tension at distance s from the tow-point at time t is denoted with T(s, t), while V_t(s, t), V_n(s, t) and V_b(s, t) are, respectively, the cable's tangential, normal and bi-normal velocities at the same point and time. Throughout we consider the plane tn parallel to the sea level and the direction of the bi-normal towards the sea bed, hence the adopted coordinate frame is obtained from the standard Cartesian (x, y, z) by an orthogonal transformation. The tangential, normal and bi-normal hydrodynamic forces on these axes are denoted by f_t(s, t), f_n(s, t) and f_b(s, t), respectively, m is the mass of the cable per unit length, θ(s, t) is a horizontal orientation angle and φ(s, t) the vertical angular displacement from that plane.

Focussing attention to the horizontal OCVPs, one may reduce its dimension by restricting the motion in the tn plane. As steering and vessel motion are confined within this plane, vertical dynamics can be compensated by projecting the force f_b to the plane of motion in the expense of a small error in the model. This requires the inclusion of buoyancy terms taking the form of scaled differences between the streamer and water weight. Upon setting φ = 0 and V_b = 0 in (1) and superimposing the buoyancy yields (2) where , ρ is the sea water density and ρ_c the cable density. In the towing system under consideration, active depth-controlling deflectors are used to maintain the depth of the cable within a fraction of a meter from the average sea surface. The deflectors used are able to account for buoyancy variations due to changes in salinity, temperature and other offsetting factors. However, the same size deflectors are not able to counteract all cross-line variations in current. In towed seismic surveys, simply increasing the size or number of these deflectors or increasing the tow speed to account for all possible variations in currents is not a viable option as the occurred strumming of the cable eventually makes the noise level on the hydrophones unacceptable. For small depth variations one may assume a neutrally buoyant cable yielding (3) At the horizontal plane, let a_t(s) = ∂V_t/∂t and a_n(s) = ∂V_n/∂t be the accelerations of the cable in the two orthogonal directions. If the interval |∂t| is taken small enough then for non-zero ocean currents |a_n| ≫ |a_t| ∼ 0, provided that the cable is towed at a constant speed. However, choosing a large time interval balances the two acceleration components by essentially averaging and assuming quasi-steady motion, albeit in the expense of temporal resolution. In particular, setting the time scale to the time required for the tow-point of the cable to traverse a distance of one cable length, leads to |a_n| ∼ |a_t| ∼ 0 and thus ignoring the inertia terms in (2) leads to small errors in the prediction of the streamer position. In the section of non-dimensionality, this time-scale normalization is addressed more rigorously. The following section provides a more detailed description of the simplified model used in this study and summarizes some of its limitations due to the adopted assumptions.

2.2. The simplified model

A two-dimensional model describing the motion of a towed, neutrally buoyant, inextensible and perfectly flexible cable dragged at a constant speed in an incompressible fluid can be derived by setting the simplified momentum equations (2) to zero. In effect, the simplified model yields the force distribution relations 1 (4) (5) and the kinematic relations (6) (7) where V_tr = V_t − u and V_nr = V_n − v are the cable's tangential and normal relative velocities with respect to the ocean's velocities u and v at the same axes. The parameter ρ is the density of sea water, d is the nominal diameter of the cable, while C_t and C_n are its tangential and normal drag coefficients, respectively. The drag and lift forces exerted on the SE admit a dynamic variation and relate nonlinearly to the velocities and angles of attack according to the hydroelastic theory 7. In the quasi-steady motion context these forces are effectively expressed as (8) (9) with the principal component of f_qd (s) aligned with t(s) and that of f_ql (s) with n(s). 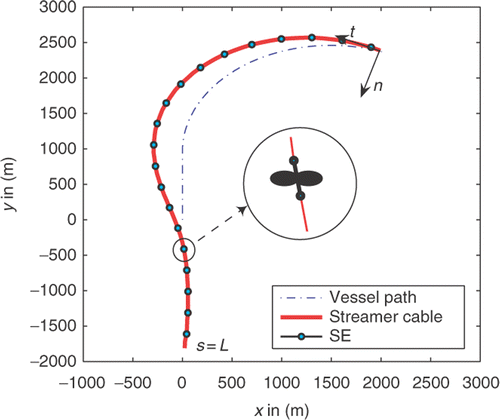In their definitions D is the diameter of the SE, g(s) ∈ {0, 1} is a binary parameter indicating the attachment of a SE at distance s from the tow-point, while C_d (α) and C_l (α) are respectively the drag and lift coefficients that relate to the effective angle of attack α (10) via the quadratic relations (11) for some non-zero parameters χ_1:31 and ψ_1:3, where α_c is the user-controlled steering angle. A typical streamer cable configuration equipped with 20 equidistant SE is illustrated in Figure 1. The model accounts also for the imposed boundary conditions, two on either end of the streamer. At the front end, the velocity of the cable relates to that of the towing vessel via (12) (13) where ν₁(t) and ν₂(t) are the cartesian components of the vessel's speed ν at time t. The tail end of the cable is not entirely free, hence the tension does not vanish as assumed in the studies of Gatti 3 and Gobat 8. We draw the attention to the fact that this model deviates from the cited studies in that the actual system incorporates a surface buoy engineered to regulate the tension and avoid the singularity. Consequently, the zero tail tension singularity reported in the quoted publications is not encountered. Instead, the tail buoy provides the tail with a strictly positive tension value that scales linearly to the norm of its velocity (14) assuming a correspondence of T_L = 2000 N at a speed of 2.57 m s⁻¹. 2Moreover, as no SE are attached to the tail there is no curvature there, hence (15) indicating also that the normal velocity of the cable at the tail end is merely due to the ocean currents. In our study, we consider the motion of a flexible cable with length L towed at |ν| ∼ 2.57 m s⁻¹ during a finite period of time, therefore we consider s ∈ [0, L] and t = [0, t_f] and initial rest conditions.

Figure 1. A 6000 m long streamer cable arrangement with 20 SE attached every 300 m, beginning at s = 100 m.

2.2.1. Limitations of the simplified model

Aside the dimensionality restriction, the adopted model neglects several phenomena that affect the motion of the cable such as extensibility, bending, shear and torsion forces, inertia, buoyancy and acceleration. Despite this, in the context of towed seismic survey, the simplified model provides a reasonable balance between realistic simulation and computational tractability. For the extensibility, the model equations assert that the tension profile along the cable satisfies T(0) ≫ T(L) > 0. Moreover, the diameter of the cable in conjunction with its Young modulus yield an axial strain in the order of 0.05% of its length. This implies an extension of 3 m in a 6 km long cable, thus ignoring extensibility yields a small error in the current prediction. Bending, shear and torsion forces have been excluded, however the analysis in 1 and 3 indicates that incorporating bending eradicates the singularity caused by the tension free tail-end boundary condition. The surface buoy at the tail end sustains a tension of about 2000 N, and thus no singularities are exhibited. The inertia is also neglected as the force required to accelerate the cable is significantly smaller compared to the tension since in realistic terms the ratio d/L is far less than C_t. The virtual inertia, or added mass of the water, is also neglected on the same grounds and with regards to the internal damping, although this is important for the vibrations of the cable, for the timescales in consideration it appears negligibly small. Certainly, restricting the motion in the horizontal plane imposes neutral buoyancy. This assumption is violated when the cable passes through water with different salinity and temperature, although the actual system incorporates depth controllers that sustain the cable near the surface. A three-dimensional implementation of the model would be necessitated for seabed towing operation where the cable is laid on the seabed before seismic acquisition, as indeed for mooring applications where the motion is evenly distributed in all directions.

2.3. Solution methodology

The simplified model (4–15) can be cast as a system of differential equations in z = (T, V_t, V_n, θ) (16) where N holds the coefficients of the temporal derivatives, M those of the spatial derivatives and Q the hydrodynamic loads Applying a stable time-space finite difference scheme yields a system of 4n nonlinear algebraic equations (17) which provided a state solution yields the next state by tracing the roots of the resulting nonlinear equations, for i = mΔt, m = 0, 1, …, Δt⁻¹t_f. The nonlinear system (17) is solved using Newton's method 9, thus assuming a reasonably small time increment Δt, every pair of consecutive state solutions satisfies (18) where τ > 0 a small positive scalar which tends asymptotically to zero as Δt → 0. From the first-order Taylor expansion of Φ, if zⁱ⁺¹ = zⁱ + δz then (19) where denotes the current state of the system to which the boundary conditions for the next state i + 1 have been imposed. The details of the numerical method can be found in various textbooks and publications 10,11 and will not be repeated here, although the methodology for the similar problem with f_qd = f_ql = 0 is explicitly addressed in 5.

2.4. The measurements

In this framework, it is important to ascertain in some detail the spatial profiles of the forward parameters; in the continuum sense, in order to ascertain: the adequacy of finite sampling and the spatial resolution of the method, the degree of smoothness in the data, and the impact of steering on the inverse problem.

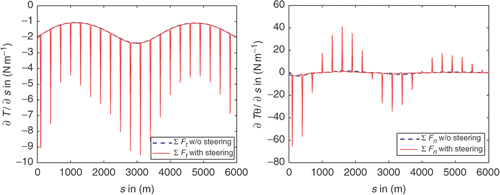
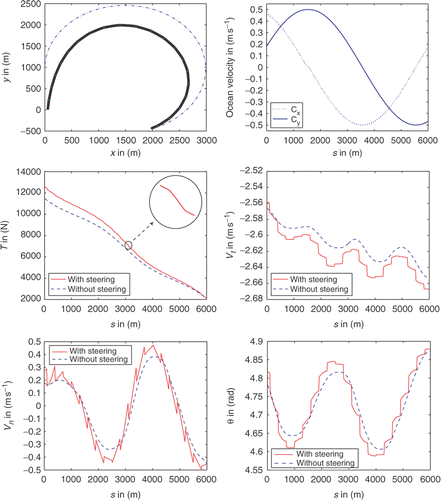
For a cable of uniform cross section towed under smoothly varying hydrodynamic drag forces, tension is a smooth, strictly decreasing function, which attains its maximum value at the tow-point and its minimum at the tail of the cable 1. Its spatial gradient is a continuous negative function related quasi-linearly to the tangential relative velocity. Under the influence of steering, tension becomes piecewise continuous strictly decreasing, with discontinuous gradient and bounded total variation . The impact of SE on the profile of the angle θ and indeed the curvature ∂θ/∂s is similar, and in regards to the velocities discontinuities are more profound in the profile of V_n. This is well anticipated as realistically most of the steering action is required to negotiate the displacements of transverse currents in order to keep the cable aligned to the trajectory of the vessel. These claims are supported by the profiles of the forward data depicted in Figure 2.

Figure 2. Forward solutions under smooth sinusoidal hydrodynamic loads. From top left: the cable trajectory at the time of measurement, the ocean currents in Cartesian coordinates, the tension, tangential velocity, normal velocity and orientation angle profiles. The dashed smooth profiles indicate the forward solutions without any steering, while the solid non-smooth lines illustrate the solutions under the influence of SE. The plots correspond to a time t = 2000 s after the start of the motion.

The introduction of SE makes the inverse problem nonlinear due to the quadratic and trigonometric dependance of the dynamically varying steering forces on u and v. Moreover, SE are usually sparsely distributed along the cable and hence steering forces have local support. Contrary to the ocean induced drag forces, their spatial profiles are highly discontinuous. Consequently, f_t and f_n are typically constituted from low frequency components; assuming relatively, smooth OCVP with long periods, while the steering force profiles occupy a high-frequency part of the spectrum. In regards to their magnitudes, steering forces are substantially higher as this is required by their design to allow for the effective control of the whole cable despite their scarce distribution along its length. Consequently, in the knowledge of ∑F_t = ∂T/∂s and ∑F_n = T∂θ/∂s the contribution of SE should be easily distinguished. The drag forces on each axis with and without steering are illustrated in the graphs of Figure 3, clearly indicating the distinctive contribution of the SE components on the resulting force profiles.

Figure 3. The total drag forces in the tangential (left) and normal (right) directions with and without steering clearly indicating the high-frequency contribution of SE.

3. Integral formulation

The approach for solving the inverse problem begins by formulating the appropriate optimization problem. In this framework, we cast the objective as a coupled system of 2(n − 1) nonlinear error residual equations of the form (20) where which evaluate the misfit in the model given the pair of OCVP and the noisy forward measurements , where z are the exact data obtained by solving the forward problem (4–15), and w is the total contribution of noise affecting the various forward parameters. Note that ℓ₁ refers explicitly to forces on the tangential axis and ℓ₂ to those on the normal, while the tilde notation in (3) marks the noisy quantities. In this context, the pair (u_*, v_*) denotes the optimum inverse solution for which the Euclidian norm of the error residuals in (20) for exact measurements falls below the error tolerance of the numerical scheme, (21) The emphasis here is to examine the behaviour of the two residuals that contain spatial derivatives of the noisy forward data. The terms and are well known to grow unbounded in norm as the noise levels in the data rise (22) essentially causing the residuals ℓ₁, ℓ₂ in their current form to be unusable for the evaluation of OCVP. Differentiating noisy data is notoriously impractical, as even small random perturbations in the differentiated variable trigger arbitrarily large oscillations in the derivative. This is a fundamental linear ill-posed inverse problems and has been thoroughly studied in numerous textbooks and publications 12,13. A robust way to compute first derivatives of discrete noisy signals, e.g. in a finite difference sense, is by recasting differentiation in the form of inverse integration via the associated ‘anti-differential’ linear operator, which has a Heaviside step function kernel scaled to the space discretization (23) Denoting the sum of tangential forces in ℓ₁ by Q_t(u, v), then the integral form of the first momentum equation becomes (24) where is the vector of discrete tension differences referenced to the tail like , A ∈ ℝ^n−1×n−1 is the discrete form of (23) based on a grid with n nodes, and R{A⁻¹} denotes a regularized inverse of the integral operator. Similarly, the integral form of ℓ₂ becomes (25) where Q_n(u, v) ∈ ℝⁿ⁻¹ is the sum of normal hydrodynamic forces acting on each element, is the mean elemental tension obtained by averaging the corresponding nodal tensions, the operator ‘Ø’ denotes element-wise division, and ‘⊙’ element-wise multiplication. Equation (25) always yields a finite answer since tension values are lower bounded away from zero. In fact, the minimum value of tension is attained at the tail and this is maintained strictly positive by appropriate control mechanisms attached to the streamer. 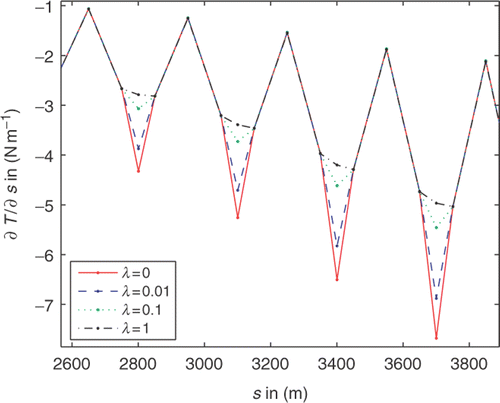In the integral residuals (24) and (25) the regularized operator can be derived by means of generalized Tikhonov regularization, given the discrete first-order difference operator R ∈ ℝ^n−1×n and an optimal relaxation parameter λ > 0 (26) The truncation of A smallest singular values performed in (26), filters to a degree set by λ the included noise and thus enforces stability in the computation of the gradients. At the same time, it also removes the high-frequency features in the gradients of T and θ, as indeed the jumps occurring systematically at the SE positions, effectively corrupting the actual measurements. The plots of Figure 4 show the gradient of the exact tension against its regularized counterpart. The rise in regularization parameter required for higher levels of noise enforces stability in the expense of rounding off the sharp edges of the exact gradient appearing at the locations of the SE.

Figure 4. The effect of Tikhonov method on the construction of the regularized integral residuals. Detail from the gradient of tension computed on a cable with L = 6000 m, having Δs = 100 and 1 m long SE, positioned at s = 2800, 3100, 3400 and 3700 m from the head of the streamer. The plots illustrate clearly the ‘rounding off’ of the gradient for increasing λ.

4. Non-dimensionalization

Before embarking on solving the inverse problem it is worthwhile taking a closer look at the two equations in (24) and (25). Beginning with the former, assume that the noisy tension signal is constructed by infusing a random perturbation so that while all positioning variables maintain their exact values. Considering also the realistic assumption ‖T‖ ≫ ‖δT‖, then at the optimum solution the residual becomes which leads to an approximate residual norm in the order of λ⁻¹, where the value of this parameter lies above the smallest singular value of A which from (23) relates linearly to the discretization size Δs. In effect, small noise perturbations in tension cause small and bounded perturbations in the value of the residual (24). Repeating the same procedure for the second residual assuming , ‖θ‖ > ‖δθ‖ yields, The above reveals that the residual is extremely sensitive to perturbations in the orientation angle, since for any non-zero δθ the error gets magnified by the tension data which are typically of several orders of magnitude higher, e.g. θ = O(2π) while T = O(10⁵). To rectify this problem the original parameters are NDM using the triplet of positive constants (a, b, c). If the superscript ‘⋄’ decorates the NDM quantities such that T^⋄ = T c⁻¹, , , s^⋄ = sac⁻¹, θ^⋄ = θb⁻¹, and A^⋄ = Aca⁻¹ then integral residuals can now be expressed as (27) From the NDM parameters only a and b are linearly independent, and thus their optimal values can be easily estimated by applying standard convex optimization techniques on (27) given the noise content in the data 9. After this treatment we are now ready to cast the forward model in an abstract form using the nonlinear residual operator Λ^⋄ : ℝ²ⁿ × ℝ⁴ⁿ → ℝ²ⁿ (28)

5. The inverse problem

5.1. Linearization

This section addresses the formulation of the inverse problem in the context of parameter estimation, where one seeks to evaluate the pair of ocean currents (u, v) that fit the NDM integral momentum equations (28) given data containing instrumentation and physically induced noise uncertainties. If X ⊂ ℝⁿ is the discrete space of admissible OCVP, it becomes clear that the desired solution is given by the minimization problem (29) Assuming that the optimal solution is situated at a small distance δ from an estimate such that u_* = u+δu and v_* = v + δv, then from a first-order Taylor expansion on the residuals we obtain (30) In fact, since the data are noisy the expansion will yield a vector with norm equal to ‖w‖, however here we consider the general case where . Some trivial algebra eventually leads to the linearized problem (31) where Λ^⋄′ ∈ ℝ^2(n−1)×2n is the Jacobian matrix, and δ ∈ ℝ²ⁿ is the column vector holding the update directions (linear step solution) in the variables of interest. The computation of δ from (31) is not feasible since the inverse of is not well defined as the Jacobian is rank deficient and ill-conditioned. Consequently, some form of regularization is necessitated for recovering a stable solution. For u,v sufficiently smooth the norm ‖Rδ‖₂ is small this can be used as a priori information to regularize (31). In effect the linearized regularized problem can be finally formulated as a constrained optimization problem, from where the optimal step solution is (32)

5.2. Algorithm for the nonlinear problem

The nonlinear inverse problem of reconstructing the ocean currents from the knowledge of noisy data is solved via Newton's algorithm for nonlinear convex problems 9,14. In this, the original problem (29) is iteratively linearized and regularized using Tikhonov regularization as in (32) until a ξ ≤ ‖w‖ is attained. Given initial or previously recovered solution (u, v), a pseudocode describing this process is given as follows:

•	Compute the regularized residual
•	Assemble the block diagonal regularization matrix
•	while ‖ξ‖ > ‖w‖ do • Evaluate • Compute linearized step • Update directions u → u + δu, v → v + δv • Update misfit
•	end.

5.3. Angle of attack prediction

In the preceding sections, we focussed attention on predicting the ocean currents from tension and positioning data. In order to allow for optimal steering, aside predicting the currents with adequate resolution, it is critical to make an accurate prediction on the angle of attack (10). From the above analysis the impact of noise on the reconstruction of currents can be established with a high level of confidence, however their influence on α is less straightforward. To accommodate realistic constraints on the operation of SE, the angle of attack is maintained within the range −1/3 ≤ α ≤ 1/3 in order to avoid stalling the SE. In this region, the arctangent becomes nearly linear. Hence, in the range of interest and for zero control angle the definition of the angle of attack can be approximated by (33) which translates to a constraint in the relative velocities ratio A useful insight into the performance of the proposed method in predicting α can thus be obtained by evaluating the sensitivity of the angle with respect to the two currents (34) Notice that the angle restriction coefficient appears only in the derivative of α with respect to the in-line currents. This implies that S^α(u) depends on the actual angle value, hinting that different angles will have different sensitivity for in-line current variations. From (34) it is easy to see that the sensitivity of the angle with respect to the cross-line currents is at least three times higher compared to that of in-line currents. Moreover, as the relative in-line velocity rises, e.g. through an increase of |ν|, both S^α(u) and S^α(v) become ‘flatter’ making the angle prediction more tolerant to noise in the expense of spatial resolution in the detected OCVP.

6. Numerical results

To assess the performance of the proposed scheme in inferring the OCVP two numerical test cases have been simulated. To aid comparison the cable configurations and vessel trajectory are maintained the same in both cases. In this, the towing vessel is set to perform a straight northbound motion at a speed of 2.57 m s⁻¹ for 8000 m, towing a streamer cable of length L = 6000 m and diameter d = 0.045 m, equipped with twenty 1 m long SE. The SE have diameter D = 0.05 m, and are distributed equidistantly at 300 m intervals. In the specification of the model, the tangential and normal hydrodynamic drag coefficients have been set to C_t = 0.006 and C_n = 2, in accordance to some experimental studies reported in 2. In the numerical simulation, a rather fine mesh was employed to solve the forward problem at the required level of accuracy while a coarser mesh was used to address the inverse problem. In particular, if s_f = s∖s_se denotes the SE-free part of the cable, for the forward problem a Δs = 10 m on s_f and Δs = 1 m on s_se were implemented, yielding a finite model with 620 linear elements, while for the inverse problem grid the discretization level on s_f was increased to 100 m resulting in a coarser grid with 80 elements. In both cases the time step was kept constant at Δt = 10 s. In the conversion of the momentum equations into their integral form, a regularization factor λ = 10⁻⁴ was used while for the NDM process the parameters were estimated at , b = 200π and c = aL.

In the first case, ocean waves with sinusoidal velocity profiles ν₁(t) = 0.5 sin(πt/3) and ν₂(t) = 0.5 cos(πt/3) impinge upon the cable while the controlled steering angle is maintained at zero. The forward simulations were implemented via finite differences at an error tolerance of 10⁻⁴, and in sequence the forward data were infused with noise, emulating realistic survey conditions. To the positioning data an additive white Gaussian noise of SD 1 m and a random walk of amplitude 1 m at a period of 200 s were introduced. The noise was used to perturb the coordinates of the nodes after each time step, essentially yielding a systematic error in the profiles of the orientation angle and velocities. For the tension data we have assumed a white Gaussian noise signal of SD equal to 1% of the mean tension value at each time step. To eradicate the impact of noise the inverse problem was solved with a regularization parameter of λ = 10⁻². This value has been optimally selected to sustain stability throughout the computations. The impact of the regularization parameter is explained and illustrated in 5 while some generic methods for its selection appear in 9,15. As the noise level was kept fixed, the choice of λ was adequate to yield the desired results, however in dealing with real measurements a routine for optimizing the regularization parameter would be more appropriate.

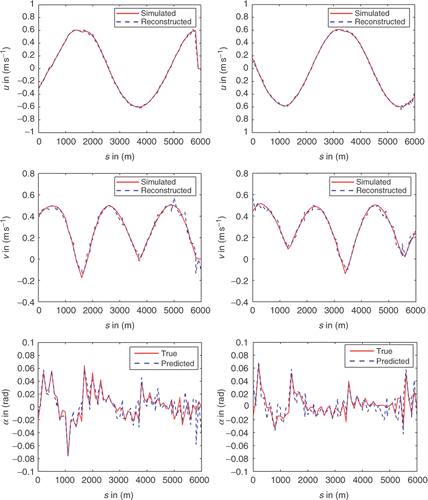
The graphs in Figure 5 correspond to the simulated and reconstructed OCVP and angle of attack at times t = 100Δt and t = 200Δt after the start of motion. These show that the smooth profile of the currents is reconstructed with adequate accuracy with this moderate amount of noise, although the quality of reconstruction in in-line currents is superior to that of the cross line. The bottom graphs of the same figure illustrate the performance of the method in predicting the angle of attack based on the measured noise contaminated cable velocities and the reconstructed regularized ocean waves. Although to some extend there is a good agreement with the simulated profile, the prediction suffers from the inaccuracies in the recovered normal currents. As expected from (34), the prediction is indeed more sensitive to the errors in the reconstructed cross-line currents, and hence accurate positioning information is critical, hence in this context the consideration of a weighted Euclidian norm residual in (29) could be a promising alternative.

Figure 5. Results from the first test case with additive noise in the data. Left column: reconstructions of OCVP u, v and angle of attack α at t = 1000 s after the start of simulation, and right the corresponding results at t = 2000 s.

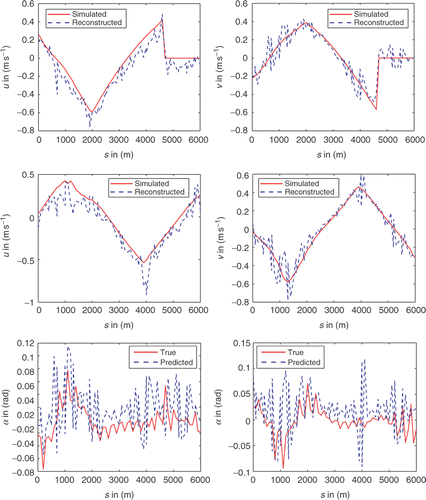
To expose some of the limitations of the proposed methodology as well as to motivate further research, a second simulated study with greater error content in the measurements was performed. Here, ocean waves of ramp function profiles were assumed in simulating the motion of the cable, and the controlled steering angle was set constant to α_c = 2.5 rad. To the additive white Gaussian and random walk noise used previously another variation was introduced. The positioning measurements were further contaminated with a correlated variation relative to the trajectory of the vessel. This error was assumed to attain its peak magnitude of 2 m at the middle of the streamer, and set to diffuse towards the two ends where more reliable GPS information is typically available. In addition, a dynamic random offset of magnitude 15% of C_t's nominal value was imposed on the tangential drag coefficient. The reconstructed OCVP obtained in this later case and the corresponding predictions on the angle of attack are presented in Figure 6 at two different time instants. In comparison to the results of the previous case, the spatial resolution is significantly compromised with the impact of the noise being more profound on the prediction of α. Despite enforcing a greater degree of smoothness the inverse solution was significantly distorted. These results show that although the low-frequency spectrum components of the reconstructed OCVPs are indicative of the target waves, there is arguably little, if any, useful information in the predicted angle of attack.

Figure 6. Results from the second test case with positioning errors and dynamic offset on the in-line drag coefficient. Left column: Reconstructions of OCVP u, v and angle of attack α at t = 800 s, and right the corresponding results t = 2000 s after the start of simulation.

In general terms, evaluating the total drag forces on the two axes, namely and , reveals that the norm of the residual is most sensitive to variations in u, while that of relies mostly on v. In effect, tension inaccuracies affect mostly that relates the in-line drag forces to the regularized gradient of tension. Similarly, involving the gradient of the angle θ dominates the error in normal currents. Hence, the imposed positioning errors have a significant impact on the gradient of the orientation angle inevitably causing a more profound deterioration on the reconstructed v.

All numerical simulations, including forward and inverse computations have been performed on a 1.8 GHz personal computer with 2 GB of RAM, running MATLAB 16. The computational cost of the algorithm is fairly low for moderately powerful computers, with the solution of the forward problem on the finer grid yielding a linear system of dimension 2500 taking on average around 1 s per time step. The temporal resolution of the inverse problem based on the coarser grid was found to be in the range of 1 s per data frame, thus well below the rate by which data are realistically acquired. It is also worthwhile quoting that the forward simulator experienced convergence difficulties in a few ‘extreme’ situations where it was provided with very coarse spatial or time discretization, or in occasions where the computed curvature of the cable became unrealistically complicated due to highly discontinuous OCVPs or intense controlled steering and abrupt vessel maneuvering.

7. Conclusion

This article addresses the inverse problem of reconstructing the OCVP on a towed streamer cable equipped with SE. Having specified the fundamental differences from the non-steered case we have shown how the conventional quasi-static hydrodynamic model can be augmented to accommodate the steering deflector elements on board the cable and indicated that these forces relate dynamically and nonlinearly on the ocean velocities. In sequence, we have demonstrated the need of casting the model momentum equations in an integral NDM form to preserve stability in the inverse solution. The resulted nonlinear residual equations were approached in the context of Newton's method with the aid of generalized Tikhonov regularization, which was shown through the numerical results to perform well for smooth current profiles. Our study has shown that in-line current resolution depends mostly on how accurately one estimates the gradient of tension, which through the introduction of SE becomes a highly discontinuous function. For similar reasons, cross-line current resolution depends on the quality one estimates the discontinuous curvature of the cable. With regards to the angle of attack, this was shown to be more sensitive to the quality of cross-line current reconstructions, while as anticipated the predicted angle of attack profile is more tolerant to errors in in-line currents.

Acknowledgements

The authors would like to express their gratitude to Smith Institute for Industrial Mathematics for organizing the ‘Study Group with Industry’ that brought together the second and third authors to work together on this problem. The authors would also like to thank Dr J.O. Paulsen of WesternGeco, Oslo Technology Center for his help and support of this work. The second author is now with Validus Engineering AS. The authors would also like to acknowledge the two anonymous referees for their remarks and suggestions in improving the quality of the script.

Notes

Notes

1. In the text, we often make use of the notation a_1:k:n to denote the incremental instances of the variable a in the closed interval [1, n], spaced by k. When k = 1, this is omitted giving χ_1:3 = χ₁, χ₂, χ₃.

2. In nautical terms this is the equivalent of five knots.