A meshless CFD approach for evolutionary shape optimization of bypass grafts anastomoses

Abstract

Improving the blood flow or hemodynamics in the synthetic bypass graft end-to-side distal anastomosis (ETSDA) is an important element for the long-term success of bypass surgeries. An ETSDA is the interconnection between the graft and the operated-on artery. The control of hemodynamic conditions through the ETSDA is mostly dictated by the shape of the ETSDA. Thus, a formal ETSDA shape optimization would serve the goal of improving the ETSDA flowfield. Computational fluid dynamics (CFD) is a convenient tool to quantify hemodynamic parameters; also, the genetic algorithm (GA) is an effective tool to identify the ETSDA optimal shape that modify those hemodynamic quantities such that the optimization objective is met. The present article introduces a unique approach where a meshless CFD solver is coupled to a GA for the purpose of optimizing the ETSDA shape. Three anastomotic models are optimized herein: the conventional ETSDA, the Miller cuff ETSDA and the hood ETSDA. Results demonstrate the effectiveness of the proposed integrated optimization approach in obtaining anastomoses optimal shapes.

Keywords:

• end-to-side distal anastomoses
• intimal hyperplasia
• shape optimization
• meshless CFD
• genetic algorithms

1. Introduction

Meshless methods are novel numerical techniques intended to eliminate the structured mesh generation task required by traditional numerical methods such as the finite volume method (FVM) and the finite element method (FEM). The meshless techniques are well suited to simulate physical phenomena for problems that involve complex geometries, surface discontinuities, large boundary deformations and shape optimizations. The advantage of using the meshless numerical technique, which solves the governing differential equations on a non-ordered set of points distributed in space, is due to the fact that it lends itself ideally to automated point redistribution 1. As such, this technique is ideally suited for shape optimization as we will demonstrate in this article through the shape optimization of bypass graft anastomoses 2. Meshless methods are still under development and they have, so far, proven to be accurate in application to traditional computational fluid mechanics and heat transfer 3–16.

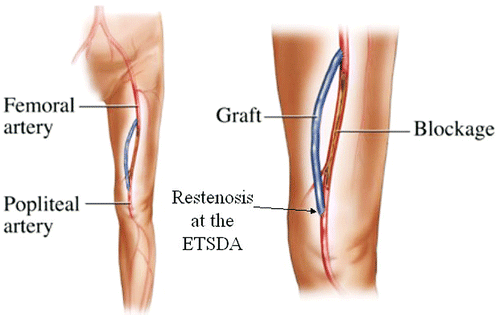
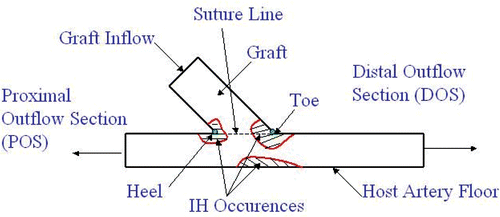
Although vascular surgeons are currently taking the path of minimally invasive endovascular procedures such as the balloon angioplasty and stenting, they still rely on bypass procedures when an endovascular procedure is simply unfeasible 17. The downside of a bypass procedure is the poor post-operative graft performance due to the occurrence of intimal hyperplasia (IH) at the end-to-side distal anastomosis (ETSDA) as depicted in Figure 1. Anastomosis is the connection of two structures, often tubular, and in our case refers to connection between the bypass graft and the arterial vessel. Hyperplasia is a medical term referring to the abnormal proliferation of cells within a tissue or an organ, while IH is the thickening of the tunica intima, the inner-most layer of the various tissues composing the arterial wall, as a complication of a surgical intervention. IH preferably localizes at both the floor of the operated-on/host artery and at the graft-artery suture line area as illustrated in Figure 2. This phenomenon was observed by many investigators such as Sottiurai et al. 18, Bassiouny et al. 19 and Trubel et al. 20. It was suggested in 20 that the IH on the floor of the host artery is purely caused by hemodynamics forces. The suture line IH is associated with the compliance mismatch resulting from the mechanical properties difference between the synthetic graft and the artery biological tissues. A comprehensive review on bypass grafts ETSDA IH can be found in Lemson 21.

Figure 1. The occurrence of IH at the ETSDA.

Figure 2. The ETSDA sites of IH localization.

The spatial wall shear stress gradient (SWSSG) is a critical hemodynamic parameter that bears consideration as its high values are indicative of the presence of disturbed flow conditions such as flow separation and reattachment, stagnation point flow and flow recirculation. The in vitro work of Tardy et al. 22 suggested that the high values of the SWSSG causes a denudation of the endothelium, which will very likely lead to an IH mechanism. In addition, the experimental work of Hsu et al. 23 demonstrated that high values of the SWSSG delay the motion of the endothelial cells that are migrating to re-generate a denuded section of the endothelium. In healthy circumstances, an undisturbed laminar flow with very low SWSSGs would result in a fast re-endothelization and inhibition of the proliferating cells 23. The experimental visualization of Ojha 24 and numerical simulation of Lei 25 for the ETSDA flowfield reveals high SWSSG values at the ETSDA host artery floor, which is practically an IH site.

In order to mitigate the hemodynamic factors believed to cause IH growth, several researchers attempted to optimize the shape of the ETSDA. For instance, the shape optimization approaches of Lei 26 and O'Brien 27 are direct ones that might not yield the optimal ETSDA shape under a given optimization objective, especially when the geometry design variables become numerous. To that effect, Rozza et al. 28 incorporated a gradient-based approach to optimize the graft shape at the ETSDA toe and their objective was to reduce the flow vorticity. Nonetheless, as the gradient-based methods locally search for an optimal solution they might lead to a premature convergence, i.e. converge to a local optimal solution that is not necessarily a global optimal solution as the optimization space might have several local maxima/minima. Consequently, a genetic algorithm (GA) optimization approach that employs a meshless technique is presently proposed to enhance the ETSDA shape. The GA is an evolutionary approach that relies on a global search for the optimal solution within a prescribed search range. The usage of the GA is more advantageous than the gradient-based methods. Due to the evolutionary aspect of the GA it becomes very hard to converge to a local optimal solution as the GA search mechanism constantly scans the global search range to uncover the global optimal solution(s).

The purpose of this article is to create a shape optimization suite that consists of a GA, a meshless computational fluid dynamics (CFD) solver, and an automated pre-processor. The application of this suite will be for the steady Newtonian flow in the ETSDA; this preliminary application lacks a number of physiological aspects, even so it serves as a test for the functionality of the proposed optimization suite. Following this introduction, a presentation of the meshless numerical method as formulated to solve the incompressible Navier–Stokes equations is followed by a brief description of the functionality and advantages of its automated pre-processor. Results are presented thereafter for the meshless method computations of the velocity fields and the wall shear stress (WSS) for laminar steady flow in three different ETSDA geometries. The meshless method results are compared to those produced by an established commercial finite volume CFD solver for validation. Subsequently, a section is stated about the features of the GA and the manner of the GA coupling to the meshless CFD solver. Finally, several shape optimization examples are executed for the three considered anastomosis models.

2. The localized meshless method numerical solution of the N–S equations

For the current ETSDA flow in peripheral host arteries, we will assume that the blood flow is steady, laminar and incompressible with no body forces accounted for. Although they are significant, the effects of pulsatile flow and non-Newtonian rheology are ignored in the flow model at this point because the technical aim of this article is to prove the concept of coupling a CFD solver to an ETSDA shape optimizer; those effects will be reported later on in the literature as the meshless CFD solver will be improved. The flow is governed by the N–S equations that consist of the continuity Equation (1) and the momentum Equation (2), (1) (2) where is the velocity vector, p the pressure, ρ the density, and μ the dynamic viscosity. Regarding the velocity boundary conditions, a volumetric flow rate is prescribed at the inlet, a no-slip condition (zero velocity) is prescribed at the wall knowing that blood is viscous, and a non-reflective boundary condition is assigned at the outlet(s).

2.1. The velocity correction scheme

In the present meshless method, the N–S equations are solved by an explicit formulation that is based on time-marching the velocity solution at each internal point through controlled time steps until a steady state is reached. For a given internal point i, an artificial velocity is estimated at every new time step k + 1 from the momentum equation by sampling the values of the convective term the viscous term , and the pressure gradient term from the previous time step k such as, (3) Note that does not satisfy the continuity equation and should be corrected. This correction is done by determining the correction potential from the Poisson equation for the mass defect, (4) Equation (3) can be explicitly solved by imposing an homogeneous second kind boundary condition type at the inlet and walls and a homogeneous first kind boundary condition at the outlet(s). When is solved, it is directly used to correct and consequently yield a velocity field that should satisfy the continuity equation, that is (5) The pressure field can be obtained by explicitly solving a Poisson equation that is obtained by taking the divergence of the momentum equation at the new time step k + 1, (6) Equation (6) can be solved by imposing a pre-determined second kind boundary condition type at the inlet and walls and a prescribed first kind boundary condition at the outlet.

2.2. Localized interpolation topologies

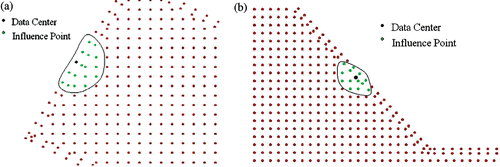
A key task when explicitly solving the artificial velocity, the potential, the corrected velocity and the pressure is to evaluate their derivatives in a stable manner. The current meshless technique relies on localized interpolations to evaluate the field variables first-order and second-order derivatives at each point on both the domain boundary and interior. What makes the meshless method stands with respect to other traditional numerical methods is its capability to interpolate the derivatives of any given field variable to a high-order of accuracy over a set of non-uniformly distributed points. Other traditional numerical techniques, such as the FVM or finite difference method (FDM), require that the solution points to be uniformly distributed or at least ordered in some sense so that derivatives can be computed with a high order of accuracy. In the current meshless technique, each point in the domain is treated as a data centre that acquires influence from a neighbouring set of points. The data centre and its influence points are grouped together in a local topology over which the interpolation is executed. The local topologies of two arbitrary boundary and internal data centres are illustrated in Figure 3(a) and (b) respectively.

Figure 3. The local topology of (a) a boundary data centre and (b) and interior data centre.

In order to suppress the oscillations arising from the non-linearity of the convective terms in the momentum equation, the local topology is further reduced to an upwind topology by appropriate skewing of the point selection and over which a solution limiter is applied. Taking the pressure field variable as an example, it can be interpolated over a local topology according to an expansion about a given data centre x_c; this expansion is illustrated in Equation (7), (7) where NF is the number of points in the local topology of x_c, α_j are the expansion co-efficients and χ_j are the expansion functions that depend solely on the geometrical position of the points within the topology. Two types of expansion functions are used for the current meshless technique: the least-squares-enhanced polynomials and radial basis functions. Those types of expansion functions can predict derivatives with a high-order of accuracy at a data centre even with non-uniformly distributed influence points in its local topology (such as shown in Figure 3). To estimate the field variable derivatives at x_c, any linear differential operator ℒ can be applied over Equation (7) such as: (8) where x_c is the data centre of the topology. The ℒ operator can be either a first-order derivative, a second-order derivative, or even a cross derivative. Thus, in a matrix-vector form: (9) Therefore, the evaluation of the derivatives at each of the data centres x_c is provided by a simple inner product of two small vectors: {ℒ} which can be pre-built and stored and {p} which is the sampled field variable through the topology of the data centre x_c from the previous time step k. A more detailed discussion of the localized meshless method as applied to the N–S equation can be found in 14–16.

2.3. The automated geometry pre-processor

The advantage of using the automated pre-processor is in its ability to re-deploy a point distribution in the physical domain of interest as it evolves in the shape optimization process without the need for user interaction. When dealing with any geometry, classical numerical techniques such as the FVM and the FDM require a well-structured body-fitted mesh in order to produce valid results. However, the process of building a body-fitted mesh usually requires interaction by the user to develop meshes in a careful manner that avoid, amongst other things, grid skewness and grid misalignment with the flow. Besides dividing the domain into multi-blocks becomes necessary in the case of a complex three-dimensional geometric model, which further makes the mesh generation task daunting and time-inefficient. Unstructured meshes provide some relief, however, to capture the boundary layer a structured meshes is still required close to the walls and moreover, unstructured mesh solvers are often too dissipative. As such, the localized meshless method we utilize in this study offers many advantages in shape optimization application.

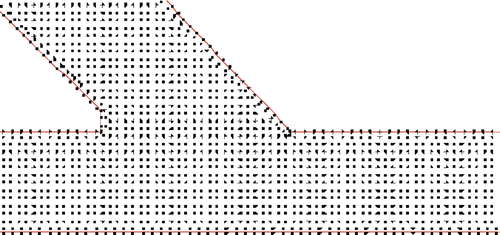
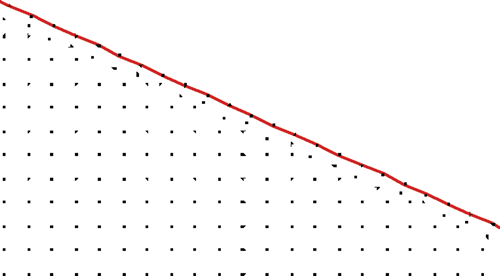
The automated pre-processor only requires the geometry information as an input. In the present two-dimensional analysis, the geometry corners coordinates and the point distribution density on each boundary edge can give the input information. Once the geometry information is specified, the boundary points will be distributed uniformly along the boundary; following its normal vector, each boundary point will then create one neighbouring shadow point in the interior. The shadow point serves to determine the normal derivatives at its corresponding boundary point. Next, the internal points are automatically created in the domain interior following a Cartesian order that is independent from the order of the boundary and the shadow points. An example showing the automated point distribution executed by pre-processor in the ETSDA vicinity is shown in Figure 4. Although the interior points seem to follow a Cartesian uniform distribution, they assume no order or connectivity with respect the boundary points as it is shown in Figure 5. This non-ordered relation between the interior and the boundary points really gives the current CFD numerical technique a ‘meshless’ aspect. Note that the Cartesian distribution of the points in the domain interior will significantly mitigate the numerical diffusion of the solution, hence putting the usage of current pre-processor at an advantage over the usage of a traditional FVM/FDM unstructured mesh generator.

Figure 4. The automated pre-processor output.

Figure 5. The order independence between the boundary and internal points.

2.4. Numerical validation of the meshless solver

Since the localized meshless method is a relatively newcomer to CFD modelling, we benchmark its results with a well-established FVM CFD solver (FLUENT 6.2) for incompressible laminar flows in identical geometries and under the same physical conditions. It is critical for the present shape optimization approach to have the meshless CFD solver produce accurate results for any general case. Three standard ETSDA models are selected for validation: the conventional model, the Miller cuff model, and the hood model. For all the current ETSDA models, the blood flow is simulated as steady and Newtonian at a Reynolds number of 450 based on the graft diameter. The blood density and dynamic viscosity are taken to be equal to 1060 kg m⁻³ and 0.004 Ns m⁻², respectively. The bypass graft diameter is specified as 6 mm for all the three anastomotic models. The host artery diameter is equal to 4 mm, which is within the diameter range of the popliteal artery (at the knee level) where bypass surgeries with synthetic grafts are usually performed. For both the conventional and Miller cuff models, the anastomotic angle is chosen to be 45°. Besides for the Miller cuff model, the cuff height is chosen to be 3 mm. For the hood ETSDA model, the geometry of the hood consists of a cubic spline that is defined by four control points c_g, c₁, c₂ and c_a. Besides the artery cut length (CL) is taken as 1.5 mm (the artery CL is the horizontal distance between the heel location and the toe location). For all the ETSDA models, we assume that there is no proximal flow due to a complete blockage of the host artery at the proximal side. The two-dimensional schematics of the conventional, Miller cuff and hood ETSDA models are shown in Figure 6(a)–(c).

Figure 6. The schematics of the three bypass graft ETSDA geometries.

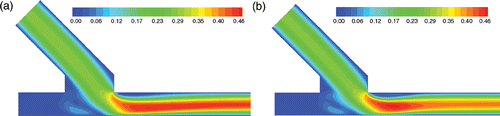
The difference in the pre-processing nature between the meshless method and the FVM is illustrated in Figures 7 and 8 for the given three ETSDA models. For the meshless pre-processing, one can notice that the distribution of the internal points is always Cartesian regardless of the geometry boundaries. For the FVM pre-processing however, the disposition of the mesh cells is dictated by the shape of the boundaries; unless the mesh propagates in a manner that fits the geometry, the FVM will yield un-converged results. In the event of a change in one or more of the geometry design variables, the internal points re-distribution for the meshless solver does not need a human effort as long as there is a simple automatic command performing a Cartesian distribution of those points. Conversely, the re-meshing of the modified geometry for the FVM solution cannot be done automatically and it does need a user to ensure a proper fit of the mesh within the modified geometry. This argument establishes the effectiveness of the meshless method in the area of GAs-based shape optimization, which will be discussed in the following section. It should be noted that the benchmark FVM solutions, against which the localized meshless CFD solutions are gauged, are obtained using the QUICK upwinding scheme.

Figure 7. The meshless point distribution.

Figure 8. The FVM meshes.

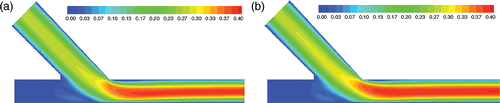
The localized meshless and the FVM results are compared qualitatively in terms of velocity magnitude, x-velocity profiles and the WSS computed on the floor of the host artery. The velocity magnitude comparison is provided in Figures 9–11 for the conventional, Miller cuff and hood ETSDA modells respectively. The velocity magnitude contours of the three ETSDA models demonstrate a very good qualitative agreement between the values predicted by the FVM and the localized meshless solvers. Particularly, the meshless method is capable of capturing the flow recirculation at the floor of the host artery consistently with the FVM. Moreover, the flow acceleration as it emerges from the graft to the artery as predicted by the meshless solver agrees well with that predicted by the FVM solver.

Figure 9. Conventional ETSDA model meshless (a) and FVM (b) velocity magnitude contours.

Figure 10. Miller Cuff ETSDA model meshless (a) and FVM (b) velocity magnitude contours.

Figure 11. Hood ETSDA model meshless (a) and FVM (b) velocity magnitude contours. Available in colour online.

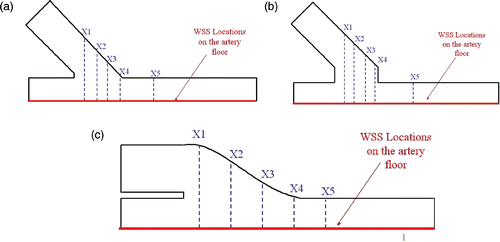
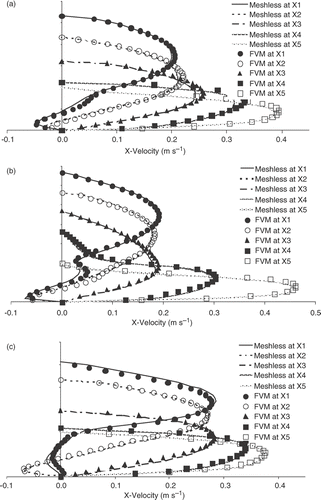
To validate the accuracy of the meshless method quantitatively, we plot the meshless and FVM x-velocity profiles at five vertical sections (X1, X2, X3, X4 and X5) across the anastomoses of the three given ETSDA models. The locations of the velocity profiles for the three given ETSDA models are revealed in Figure 12(a)–(c). The velocity profiles results are shown for the conventional ETSDA model, Miller cuff ETSDA model and the hood ETSDA model in Figures 13(a)–(c) respectively. Although minor discrepancies are evident, the velocity profiles indicate a high level of quantitative agreement between the meshless method and the FVM.

Figure 12. The x-velocity profiles and WSS locations for the three ETSDA models.

Due to the adverse effects of its spatial and temporal gradients on the endothelium, we benchmark the meshless results of the WSS at the floor of the host artery with the WSS results generated by the FVM solver for all the ETSDA models. The development of the IH on the host artery floor is thought to be purely caused by fluid mechanics factors, unlike the situation at the suture line where injury and graft-artery compliance mismatch play a main role. 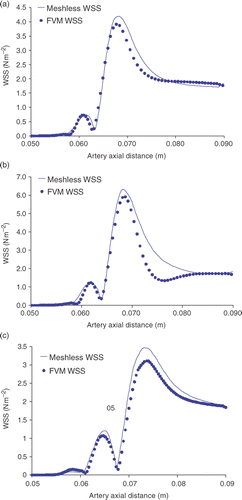The two-dimensional WSS magnitude is expressed such as: (10) where is the traction vector and its x and y components are: (11) (12) where n_x and n_y are respectively the x- and y-components of the outward drawn unit normal vector at the boundary. The meshless and FVM plots of the WSS for the conventional, Miller cuff and hood ETSDA models on their host artery floors (marked by the red line in each of Figure 12(a)–(c) are presented in Figure 14(a)–(c), respectively. The WSS results in Figure 14 reflect an acceptable agreement between the meshless method and the FVM. The minor discrepancies in the WSS between the two methods is directly attributed to the discrepancies found in the x-velocity profiles already pointed out in Figure 13. Should the x-velocity profiles perfectly match, there will be no differences in the WSS as extracted from both methods.

Figure 13. The x-velocity profiles for the three ETSDA models.

Figure 14. Meshless and FVM WSS plots at the artery floor for all the three ETSDA models.

3. The GA-based ETSDA shape optimization

3.1. The operation of GAs

Genetic algorithms are evolutionary optimization techniques, that is they utilize ideas and take inspiration from the natural evolution of living systems. Evolutionary optimizations are well suited to the optimization of systems that exhibit high non-linear behaviours and they are characterized by several features that distinguish them from other optimization algorithms. First, they work with an assembly of different solutions, this is called the population of individuals, instead of only working with a single individual representing one solution. Second, there is communication and information exchange among individuals in the population. Such communications and information exchange are the result of the individuals selection and/or recombination at each generation of the evolution. Third, all the evolutionary optimization algorithms converge to a final generation mostly consisting of ‘elite individuals’ that represent the best solutions.

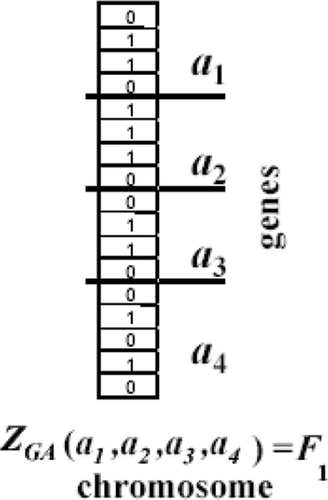
A comprehensive review and insight on the GA can be found in Goldberg 29. For a shape optimization application, the GA process begins by randomly setting an initial population of possible individuals, where each individual represents a random geometry defined by a set of design variables. This population maintains the same number of individuals as it evolves throughout successive generations. Each individual is referred to as a ‘chromosome’ containing the binary representation of its design variables referred to as ‘genes’ of the chromosome to which genetic operators are applied. Figure 15 illustrates the genetic encoding of a given individual or chromosome. Each design variable is bounded with a minimum and a maximum value, forming a search range for the optimal solutions are sought. The genetic representation of the problem will be crucial to the success of the GA. The fitness, F₁, of each individual in the population treated by the GA is evaluated through an objective function, Z_GA.

Figure 15. Example of an individual characterized by four genes encoded in a chromosome.

A typical GA relies on an iterative approach and at each iteration, the processes of selection, cross-over and mutation operators are used to alter the individuals optimization parameters such that Z_GA is minimized 30. A selection operator is first applied to the population in order to determine and select the individuals that are going to pass information in a mating process with the rest of the individuals in the population. The probability of being a selected individual is calculated as the ratio between the value of the fitness function of each individual and the sum of all objective function values. A weighted roulette wheel is generated, where each member of the current population is assigned a portion of the wheel in proportion to its probability of selection. The wheel is spun as many times as there are individuals in the population leading to the survival of the best chromosomes and the death of the worst ones. The selection process could be elitist whereby a number of the selected individuals are transferred directly to the new generation without undergoing the cross-over and mutation processes 31,32. The elitist selection approach has been proven to speed-up the GA convergence by preventing the loss of the identified good solutions 33. The selection approach employed in this article is not formally elitist as only the best selected individual is directly transferred to the new generation. For the rest of the selected individuals which have not been directly transferred to the new generation, the cross-over or mating process starts to allow the genetic information contained of those individuals to be combined and hence generate offsprings. The mutation is the final operator that is applied to randomly affect the information obtained by the mating of individuals for further genetic improvement. Two types of mutations are commonly utilized in GA's 29,34: the creep mutation and the jump mutation. With regards to creep mutation, a creep probability is assigned to every bit of each individual/chromosome in the population; if the mutation is effective, the bit will be switched from 0 to 1 or vice-versa. This process is implemented by generating a random number within the range (0, …,1) for each bit within the chromosome. If the generated number is smaller than the mutation probability the bit is mutated. Concerning the jump mutation, a jump probability is applied to every chromosome/individual in the population. If the jump mutation is effective, all bits within the chromosome/individual are switched from 0 to 1 and vice-versa. Djurisic 31 introduced an adaptive mutation technique by which each gene within of a newly-born individual is mutated based on that gene average value for all the individuals within the given population. Following selection, crossover and mutation the new population is ready for its next evolution until the convergence criteria ‘fitness’ is reached. In summary, the GAs can be applied as follows:

1.	Generate the initial population P(0) at random and set i = 0
2.	REPEAT a. Evaluate the fitness of each individual in P(i). b. Select parents from P(i) based on their fitness as follows:Given the fitness of n individuals as F1, F2, …, Fn. Then, select individual i with probability expressed in Equation (13) (13) This is often called roulette wheel selection. c. Apply CROSSOVER to selected parents. d. Apply mutation to crossed-over new individuals. e. Replace parents by the offspring to produce generation P(i + 1).
3.	UNTIL the desired criterion is satisfied.

3.2. The ETSDA shape optimization objective function

Having already discussed the damaging impact of the SWSSG on the endothelium, an ideal objective to be achieved by shape optimization of the ETSDA would be to arrive at a geometry that minimizes the high values of this hemodynamic wall parameters on the floor of the host artery. The two-dimensional SWSSG magnitude is expressed as: (14) The SWSSG is essentially a tensor, and the expression of its magnitude in Equation (14) only considers the tensor entries that tangentially affect the endothelial cells. Kleinstreuer et al. 35 discussed the formulation of the current SWSSG magnitude expression. Examining Figures 9–11, one can predict high SWSSG values at the floor occurring near the disturbed flow area where there is a flow recirculation and a stagnation point resulting from the flow impingement. On the other hand, the SWSSG values are expected to drop in the dead zone area at the host artery proximal side near the blockage and towards the outlet at the host artery distal side where the flow tends to regain its laminar parabolic shape. Plots of the SWSSG values for typical and optimal shapes of the conventional, Miller cuff and hood ETSDA models are shown in Figures 19, 22, and 26, respectively; note the spiking SWSSG values at the artery floor section across from the suture line (flow impingement site) as well as the SWSSG small values near the designated outlet at x = 0.009 m (recovered parabolic flow site). Thus, we would like to formulate a shape optimization objective function that represents the high values of the SWSSG at the host artery floor section where IH tends to develop. The objective function can be selected as the L₂ norm of the SWSSG magnitude at every boundary node on the host artery floor section that is opposite to the suture line; we call this section as the ‘floor optimization section’. Thus, the objective function, F, can be expressed as: (15) where N_BF is the number of boundary points on the floor optimization section. The magnitude values of SWSSG are controlled by the design variables of the ETSDA. After all, the anastomotic geometry plays a big role in modifying the fluid mechanics parameters at the boundary walls. Hence, F implicitly depends on the ETSDA design variables that control the magnitudes of SWSSG.

Figure 16. The IPL flowchart.

Figure 17. The conventional ETSDA model generatrix.

Figure 18. The convergence history for all the conventional ETSDA model cases.

Figure 19. SWSSG plots for the standard and optimized conventional ETSDA models.

Figure 20. The generatrix of the Miller cuff ETSDA model.

Figure 21. The objective function drop for all the Miller cuff ETSDA model cases.

Figure 22. SWSSG plots for the standard and optimized Miller cuff ETSDA models.

Figure 23. The generatrix of the hood ETSDA model.

Figure 24. The objective function minimization for all the hood ETSDA cases.

Figure 25. The optimized hood shapes for the reference and the four supportive cases.

Figure 26. SWSSG plots for the standard and the optimized reference hood ETSDA models.

3.3. The ETSDA shape optimization objective function

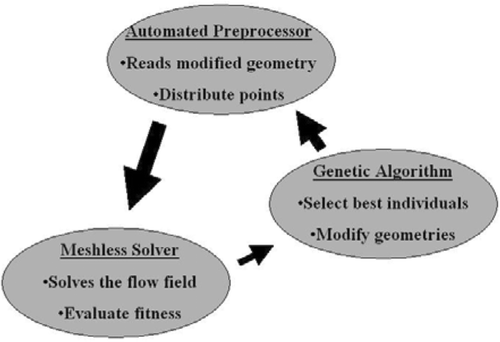
The current shape optimization is based on an information passage loop (IPL) that is comprised of three different computational objects: (1) the automated pre-processor, (2) the meshless solver and (3) the shape optimization genetic algorithm (SOGA). The goal of establishing the IPL is to provide a tool that can iteratively search for the optimal ETSDA shape within a design variable search range. This search should be autonomous from beginning to end, without any user intervention, see Figure 16, for a simple flowchart.

This GA-based optimization starts by setting an initial population of individuals, each representing an ETSDA geometry. Each individual or geometry possesses genes that represent its design variables. The initial population of ETSDA geometries undergoes an evolution throughout several generations following an iterative process, where each generation is considered as an iteration. At each iteration of this evolutionary process the following three tasks are executed within the IPL. First, the automated pre-processor reads the geometry of each ETSDA geometry and performs a point distribution therein. Second, all the ETSDA pre-processed geometries are exported to the meshless solver where the flow field is solved within each model. Once the flow field is solved, the SWSSG magnitudes on the host artery floor are post-processed and the fitness function is evaluated for each individual. It should be noted that the fitness function value for each individual is simply computed as the inverse of the objective function value. Third, all the ETSDA fitness function values are sent to the SOGA where the selection, mating and mutation processes occur leading to a new modified set of design variables. This new set of design variables is passed to the automated pre-processor to again start a new iteration. It is important to mention at this point that without having an automated pre-processor, it would not be possible to establish the IPL in an autonomous fashion. In other words, without the automated pre-processor, the user will have to intervene at every iteration to interactively pre-process the geometries which design variables have been modified by the SOGA. This intervention will make the current optimization tool highly inefficient.

The shape optimizations of the conventional, Miller cuff and hood ETSDA models depend on a set of design variables that control their geometries. Those design variables are limited by a search range over which the optimal shape of the ETSDA has be located. The search ranges for the three ETSDA models considered in this article are chosen arbitrarily. In the event of a patient-based peripheral bypass surgery, the search ranges should be set up to the discretion of the vascular surgeon, who is the principal person to estimate the surgical feasibility. For all the three ETSDA models, a population with a fixed size of 34 is chosen. The jump and creep mutation probabilities for the current GA-based optimization are taken as 0.02 and 0.2, respectively. Also, the host artery diameter is taken as constant and equal to 4 mm for all the three anastomotic models and the inlet volumetric flow rate is taken as 480 mL/min⁻¹ (corresponding to a graft-diameter-based Re number of 450).

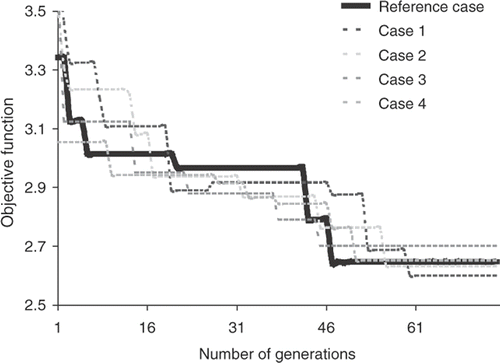
For each of the three ETSDAs shape optimizations there is one reference case and four supportive cases. The purpose of the reference case is to establish a basic convergence history of the objective function and use it as a basis of comparison. The four supportive cases are run to support the consistency argument of the algorithm. All the reference and supportive cases follow the same composed objective function and they operate in the same search ranges. The only difference between each of these cases is the initial population which the evolutionary optimization algorithm starts off. The convergence consistency should give more confidence in the identified optimal variables. There is no preset convergence criterion, rather each optimization run is allowed 75 generations. While this might not lead to the absolute optimal solution, a significant drop in the objective function should be noted through the 75 generations. A limitation for not allowing a larger number of generations is the CPU time consumed by the numerical solution of the N–S equation; this numerical solution is inevitable as there is no analytical or empirical approaches to assess the SWSSG values in an intricate geometry such as the one in the ETSDA.

3.3.1. The conventional ETSDA model shape optimization results

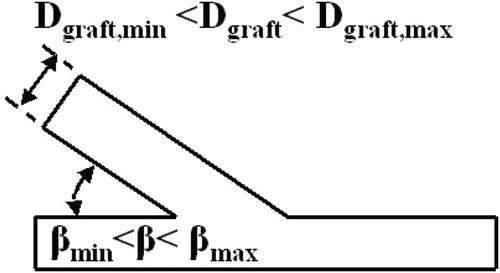
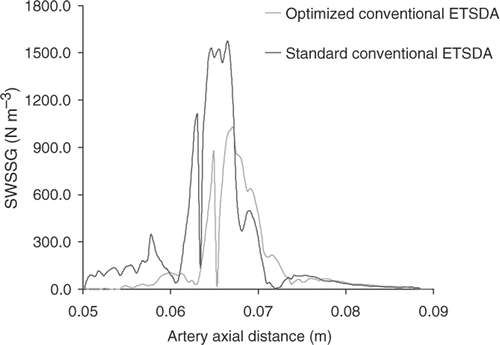
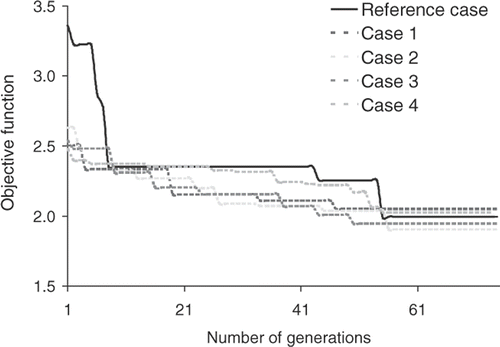
The set of design variables for the conventional ETSDA model consists of two parameters: the anastomotic angle, β, and the graft calibre D_graft. The search range for β is limited between 30 and 60°, whereas the search range for D_graft is limited between 4 and 6 mm. The generatrix of the Direct ETSDA model is shown in Figure 17. The predicted optimization outcomes and statistics at the 75th generation for the conventional ETSDA optimization variables are reported in Table 1. The convergence history of the reference and supportive objective functions for the conventional ETSDA shape optimization are displayed in Figure 18. In order to illustrate the gain achieved by the conventional ETSDA shape optimization, we plot in Figure 19 the SWSSG values on the floor optimization sections of both the current optimized shape and a selected standard shape considered for optimization. We choose the standard shape to be the one shown in Figure 6(a) (β=45° and D_graft=6 mm). Although both SWSSG plots in Figure 19 exhibit similar trends, notice that the red curve (corresponding to the standard shape) has been lowered to the level of the blue curve (corresponding to the optimized shape) thanks to the shape optimization process.

Table 1. Shape optimization results and statistics for the conventional ETSDA model.

	Graft diameter (mm)	Angle (°)
Reference case	5.96863	30.71
Case 1	5.96500	31.57
Case 2	5.73100	32.31
Case 3	5.90000	31.78
Case 4	5.75700	30.67
Mean value	5.86433	31.41
Standard deviation	0.11356	0.71

A conclusion can be withdrawn from the conventional ETSDA optimization results that the optimized shape tends to take the lower limit of β and the upper limit of D_graft. To reinforce this conclusion, a supplemental optimization solution was carried out with wider variable search ranges whereby D_graft and β were allowed to vary respectively within the following search ranges [3–7 mm] and [20–70°]. The resolved optimal values were identified as 6.937 mm for D_graft and 20° for β. Therefore, it can be concluded that a conventional ETSDA model should have the lowest possible angle and the highest graft diameter for a minimal SWSSG at the host artery floor.

3.3.2. The Miller cuff ETSDA model shape optimization results

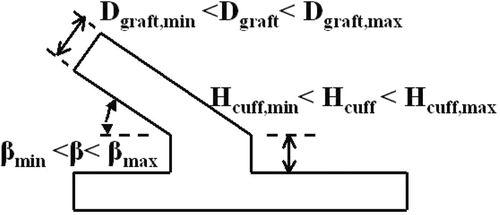
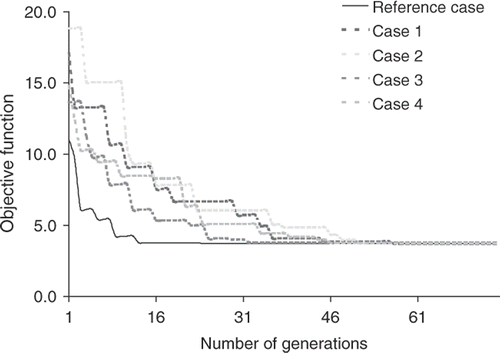
The set of design variables for the Miller cuff ETSDA model consists of three parameters: the anastomotic angle, β, the graft calibre D_graft and the cuff height, H_cuff. The cuff is made of a vein material that is interposed between the bypass graft and the host artery. The purpose of using the Miller cuff is to reduce the compliance mismatch between the synthetic graft material and the biological material of the host artery. Reducing the compliance mismatch with the Miller cuff have proven better post-operative performances of synthetic bypass grafts 36. Similarly to the conventional ETSDA model, the search range for β is limited between 30 and 60°, and the search range for D_graft is limited between 4 and 6 mm. Besides the search range for H_cuff is set between 3 and 6 mm. The generatrix of the Miller cuff ETSDA model is shown in Figure 20. The predicted optimization outcomes and statistics at the 75th generation for the Miller cuff ETSDA optimization variables are reported in Table 2. The convergence history of the reference and supportive objective functions for the Miller cuff ETSDA shape optimization are displayed in Figure 21. Considering the Miller cuff ETSDA shape shown in Figure 6(b) as a standard model, the SWSSG reduction due to the shape optimization process is revealed in Figure 22.

The Miller cuff ETSDA optimization results may be inferred such that the optimized shape tends to take the lower limits of both β and H_cuff as well as the upper limit of D_graft. To endorse this argument, a supplemental optimization solution was carried out with wider variable search ranges. As such, D_graft, β and H_cuff were allowed to vary respectively within the following search ranges [3–7 mm], [20–70°] and [2–7 mm]. The resolved optimal values turned out to be 7 mm for D_graft, 20° for β and 2 mm for H_cuff. The results of this supplemental case endorsed the observation offered for the original reference and supportive cases in regards to the optimal solution trend.

3.3.3. The hood ETSDA model shape optimization results

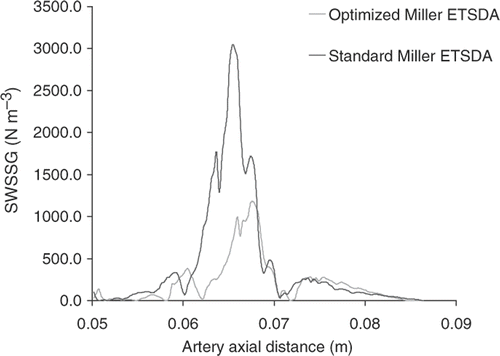
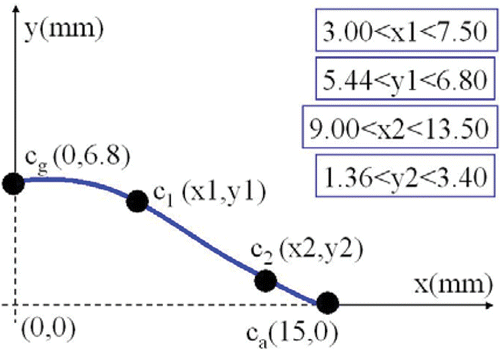
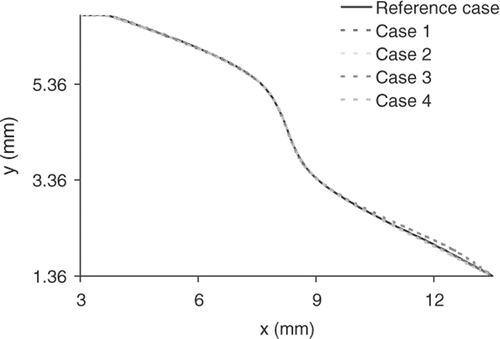
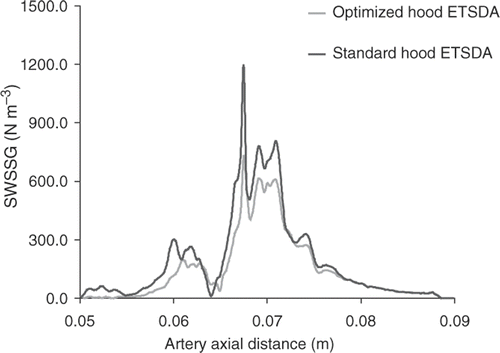
For the hood ETSDA model, we adapt a fixed diameter of 6 mm for the graft. Given a CL of 15 mm, the anastomosis shape variability only depends on the cubic spline defining the hood shape. The two end control points of the spline c_g and c_a are kept fixed whereas the other two control points c₁ and c₂ are allowed to move within limited specified two-dimensional ranges. The ranges of motion for c₁ and c₂ are specified within a two-dimensional coordinate system representing the ETSDA hood model generatrix that is shown in Figure 23. The predicted optimized coordinates and statistics at the 75th generation for c₁ and c₂ are reported in Table 3. The convergence history of the reference and supportive objective functions for the hood ETSDA shape optimization are displayed in Figure 24. Additionally, the optimized shapes of the reference and supportive cases are revealed in Figure 25; the prominent similarity of those shapes illustrates the convergence consistency of all the considered hood ETSDA shape optimization cases. The hood ETSDA model shown in Figure 6(c) is picked as a non-optimal shape; the coordinates of the moving control points of this model are: x1 = 3.75, y1 = 6.12, x2 = 11.25 and y2 = 1.36. Plots of the SWSSG on the host artery floor of both the standard and the optimized hood ETSDA models are shown in Figure 26. The narrow modification from the standard hood ETSDA shape to the optimized hood ETSDA shape justifies the slight drop in the SWSSG values in Figure 26.

Table 2. Shape optimization results and statistics for the Miller cuff ETSDA model.

	Graft diameter (mm)	Angle (°)	Cuff height (mm)
Reference case	5.90588	32.94120	3.05882
Case 1	5.96100	31.82000	3.50000
Case 2	5.71200	31.69000	3.26700
Case 3	5.73900	30.70000	3.38100
Case 4	5.73900	32.71000	3.17000
Mean value	5.81138	31.97224	3.27536
Standard deviation	0.11366	0.89507	0.17298

Table 3. Shape optimization results and statistics for the hood ETSDA model.

	x2 (mm)	y2 (mm)	x1 (mm)	y1 (mm)
Reference case	12.378	1.857	4.027	6.717
Case 1	12.538	1.782	3.951	6.731
Case 2	12.434	1.936	4.065	6.710
Case 3	12.326	1.881	3.950	6.718
Case 4	12.416	1.810	3.965	6.723
Mean value	12.419	1.853	3.992	6.720
Standard deviation	0.07867416	0.06040085	0.05167812	0.008107732

4. Conclusion

The shape improvement of the bypass grafts ETSDA can lower morbidity and reduce medical costs for patients suffering from peripheral vascular diseases. Therefore, a serious effort should be taken to address this shape optimization subject. In this article, shape optimizations for the conventional, Miller cuff and hood ETSDA models were performed to inhibit IH growth on the host artery floor. The focus on the floor of the host artery is because IH thereat is mainly affected by hemodynamic forces. The present shape optimizations are based on a GA and their objective is to reduce the SWSSG on the floor of the host artery. The current optimization approach has proven to be successful in terms of building the communication between three different computational objects: the automated pre-processor, the meshless CFD solver and the SOGA. At the time being, we cannot extend recommendations to vascular surgeons on how to design their arterial anastomoses; however future recommendations will be potentially made once the blood pulsatility and the graft-to-artery compliance mismatch are accounted for in the optimization process. The study reported herein establishes the methodology as a viable means of achieving optimal ETSDA shapes. We leave the aspects of pulsatile and non-Newtonian flow to a follow-up study.