Abstract
In this study, a new finite element model for transient heat conduction problems is presented by the inverse method. The main advantage of this method is to minimize the discretization error in the general discretized equation with no use of the element shape functions in constructing the element matrices. In order to achieve the optimum terms for the element matrices, the inverse discrete model approaches the continuous model as much as possible. The inverse formulation yields more accurate eigenvalues than the consistent and lumped formulations. In addition, it reduces the violation of physical reality in solution process when compared with consistent formulation. Finally, it is shown that the performance of the results obtained on the basis of the new bilinear rectangular element matrices is superior to the consistent and lumped finite element formulations.
Nomenclature
| x, y | = | = space coordinates |
| t | = | = time |
| T, Ti,j | = | = temperature vector, temperature at node (i, j) |
| Tx, Ty | = | = transformation matrices |
| K, Ke | = | = global and element conductance matrices |
| C, Ce | = | = global and element capacitance matrices |
| = | = lumped, consistent, and mixed element capacitance matrices | |
| kij, cij | = | = terms of the element matrices |
| f | = | = global force vector |
| Δx, Δy | = | = element dimensions |
| r | = | = element aspect ratio |
| h | = | = element thickness |
| k | = | = thermal conductivity |
| ρ | = | = density |
| c | = | = specific heat capacity |
| α | = | = thermal diffusivity |
| A, m | = | = area and mass of the element |
| I, Ik, Ic, If | = | = functional, conductance energy term, capacitance energy term, boundary energy flow term |
| ϕi, Φc | = | = constant temperature modes |
| O(i) | = | = i-th order of the general discretized equation |
| G0, G2, G4 | = | = governing continuous equation and its second- and fourth-order derivatives |
| ηi | = | = weighting coefficients |
| θ | = | = weighting parameter |
| λi, | = | = computed and analytical eigenvalues |
1. Introduction
A parabolic diffusion equation can be transformed into a time-dependent system of ordinary differential equations (ODEs) by applying any finite element method, as follows
(1)
where T is the unknown temperature vector, t is the time, K is the global conductance matrix, C is the global capacitance matrix, and f is the global force vector. Note that the obtained ODEs can be solved using various numerical techniques.
The finite element model of the heat conduction problem usually ignores the physical reality governing in a short period of time and yields oscillatory results in the solution process. A few researchers Citation1–4 have presented several criteria to select the proper scheme and time-step needed to reach an accurate solution for the system of ODEs (1). The criteria have been presented in Citation5 to determine the operating regions of the critical time-step size on the basis of the positive coefficient rule of a physical phenomenon. It was shown that by approaching the time-step to zero, the various numerical solution schemes based on the standard finite element method generates unrealistic results in both the high order element models and consistent formulations.
Various forms of stabilized finite element methods have been developed to improve the accuracy of standard finite element methods Citation6–11. The stabilized formulations can be driven by the fact that the time-discrete equations at small time-steps closely resemble a singularly perturbed problem. It should be noted that these stabilized formulations lead to semi-discrete Galerkin approximations that are free of non-causal oscillations at small time-steps. Furthermore, since the corresponding stabilization parameter relies on the time-step size, the stabilized formulations are based on pathologies of numerical difficulties. Although the accuracy of the numerical finite element solution can be achieved by a stabilized formulation, this unwanted problem remains, provided the system of ODEs (1) is analytically solved to eliminate the role of time-step size. In other words, this problem is an intrinsic characteristic of finite element formulation in time-dependent problems which must be modified in element formulation by using an inverse method. In addition, the selection of the different shape functions for each of the conductance and capacitance matrices mainly influences the accuracy and the rate of convergence of the finite element solution.
An accurate plate element model has been obtained by Ahmadian et al. Citation12 to minimize the disretization error in the element formulation. The inverse formulation of a linear one-dimensional element for transient heat conduction problems has been introduced by Madoliat and Ghasemi Citation13. Kim Citation14, Hansson and Sandberg Citation15, and Fried and Leong Citation16 have shown that a non-consistent mass matrix constructed by a linear combination of the lumped and consistent mass matrices improves the accuracy of the natural frequencies of the structural modes.
In the inverse formulation, a generic element model is firstly built by satisfying certain physical requirements. Then the general discretized equation is obtained by using the Taylor series expansion of temperatures at each of the surrounding nodes in terms of the temperature of a reference node. The unknown terms in the generic element model can be identified by comparing different orders of the general discretized equation with the governing continuous equation and its corresponding order derivatives. This element formulation gives a small dicretization error and a small difference between the continuous and discrete models.
In the present study, a new bilinear rectangular element model is presented for two-dimensional diffusion problems by the inverse method without affecting any numerical considerations. Furthermore, it is presented as a mixed-inverse formulation to determine the weighting parameter of the linear combination of the lumped and consistent capacitance matrices. The results of the inverse and the mixed-inverse methods are compared with the consistent and the lumped methods.
2. Generic element model
The present method is independent of the type of boundary and initial conditions and is concerned with homogeneous and isotropic medium along with fixed uniform grids. Consider a bilinear (four-node) rectangular element with dimensions Δx and Δy, the area A = Δx Δy, the thickness h, the density ρ and the specific capacity c. The conductance and consistent capacitance element matrices are given using the standard bilinear shape functions, as follows
(2)
where r = Δy/Δx and m = ρ h Δx Δy are the aspect ratio and mass of the element, respectively. The corresponding lumped capacitance matrix obtained by the conventional row-sum technique has the form of
(3)
In this study, according to Equations (2) and (3), consistent formulation is concerned with the Ke and
whereas lumped formulation is concerned with the Ke and
when their assembled forms are used in the system of ODEs (1). Note that the inverse formulation is not reliant on choosing the shape functions in constructing the element matrices. Thus, in order to obtain the inverse element matrices, the conductance and capacitance matrices of the element are first written in the general form as
(4)
where kij and cij (i, j = 1, …, 4) are 32 unknown terms of the element matrices which must be identified. The corresponding variational statement of a diffusion problem can be given in three parts: the conductance energy term Ik, the capacitance energy term Ic and the boundary energy flow term If, expressed in the matrix form as follows
(5)
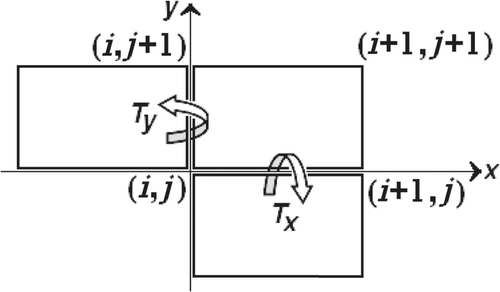
The symmetry of the element matrices, Ke = KeT and Ce = CeT, is guaranteed due to the symmetry of the scalar functional I. Hence, the unknown terms can be reduced to 20 ones as k11, k12, k13, k14, k22, k23, k24, k33, k34, k43, c11, c12, c13, c14, c22, c23, c24, c33, c34 and c43 after applying the symmetry considerations. As shown in , when the element rotates 180° about the axes of symmetries (x-x) and (y-y) by applying the transformations Tx and Ty, the element matrices remains unchanged.
(6)
Then, the comparison of the transformed matrices with the original ones which may be expressed in the forms of Ke =
Ke Tx, Ke =
Ke Ty, Ce =
Ce Tx and Ce =
CeTy gives the relations k44 = k11, k34 = k12, k24 = k13, k33 = k22, k22 = k11, k14 = k23, c44 = c11, c34 = c12, c24 = c13, c33 = c22, c22 = c11 and c14 = c23. These relations can reduce the number of the unknown terms to 8 as k11, k12, k13, k23, c11, c12, c13 and c23.
Consider an element with n constant temperature modes, ϕi, i = 1, …, n. The capacitance matrix is positive-definite, while the conductance matrix is positive-semi-definite. In general, the constant modes of the element represented by Φc = [ϕ1, …, ϕn] span the null-space of the conductance matrix. It is worthwhile noting that in the constant modes, there is no heat flux in the element. Furthermore, when the quadratic form of the constant modes is applied to the capacitance matrix, the total capacity of the element is collected on the principal coordinates of the element. Therefore, the conductance and the capacitance matrices should meet the following requirements
(7)
Note that the element has one constant mode, Φc = {1, 1, 1, 1}T. From Equation (7), one may obtain
(8)
Therefore, the generic model of a bilinear rectangular element with six unknown terms k11, k12, k13, c11, c12 and c13 containing a family of acceptable models can be driven as follows
(9)
(10)
3. Discretization error in the inverse formulation
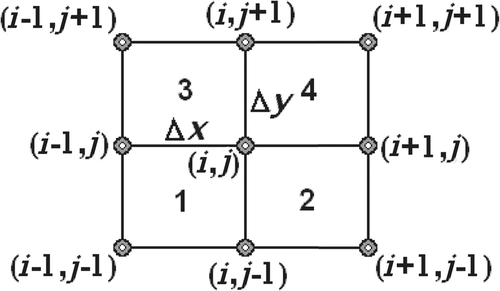
In order to achieve the general discretized equation, four bilinear rectangular elements are assumed, as shown in . The global nodal temperature vector related to the assembled model can be expressed as
(11)
The temperature at each surrounding node (m, n), in which m = i − 1, i, i + 1 and n = j − 1, j, j + 1, can be written in terms of the temperature and its derivatives with respect to x and y, at the reference (central) node (i, j) by using the Taylor series expansion
(12)
By substituting this equation into the system of ODEs (1), the general discretized equation of the reference node (i, j) is obtained. The second-, fourth- and sixth-orders of general discretized equation are given by
(13)
(14)
(15)
The governing continuous equation and its second-order derivative for the reference node (i, j) can be summarized in the forms of G0 and G2, as follows
(16)
By comparing the different terms of the second- and fourth-orders of the general discretized equation, Equations (13) and (14), with G0 and G2, the following equations are obtained as
(17)
(18)
(19)
(20)
(21)
(22)
(23)
The unknown weighting coefficients η1 and η2 are used to reduce and handle the residual errors in the discretized equations. The following relations are obtained by solving the Equations (17–23)
(24)
(25)
(26)
The fourth-order derivative of the governing continuous equation, G4, is used to determine the last unknown term c11 of the element matrices
(27)
After comparing the sixth-order of the general discretized equation, Equation (15), with G4 and using the unknown weighting coefficient η3, the following equations are obtained
(28)
(29)
(30)
(31)
(32)
(33)
(34)
The reliable value for the unknown weighting coefficient η3 can be achieved by applying the least-squares method to Equations (28–30) and (32–34), as follows
(35)
By substituting Equation (35) into Equation (31), c11 can be obtained. Then, the optimum element matrices are given by using the inverse method in the form of
(36)
(37)
For unit aspect ratio (r = 1), the weighting coefficient η3 is equal to 246; and the capacitance matrix is derived as follows
(38)
4. Discretization error in the mixed-inverse formulation
Recently, in some research studies Citation8–11 the linear combination of the lumped and consistent capacitance matrices, named as non-consistent (mixed) capacitance matrix, has been suggested to yield more satisfactory results for eigenvalues of the eigenproblem K x = λ C x with the global matrices. The mixed capacitance matrix is applied to the inverse finite element formulation in order to present a mixed-inverse method as follows
(39)
where θ is the unknown weighting parameter; θ = 1 and θ = 0 correspond to the lumped and consistent formulations, respectively. In references Citation9–11, the weighting parameter θ has been given for the total number of the considered eigenvalues, N, by
(40)
However, in this study the weighting parameter θ is determined through minimizing the disretization error in the element formulation. If the mixed capacitance matrix
is used instead of the generic capacitance matrix, given in Equation (10), the unknown terms of its generic form will be reduced from three (c11, c12 and c13) to one term (θ). Thus, the second-order term of the general discretized equation can be derived in the same way as Equation (13). After comparing Equation (13) with the governing continuous equation, Equations (17) and (18) can be similarly extracted. Then, the fourth-order of the general discretized equation of the reference node (i, j) is derived as
(41)
By comparing the different terms of this equation with G2 and using the unknown weighting coefficient η2, the following equations are obtained as
(42)
(43)
(44)
(45)
(46)
Solving these equations leads to obtain the unknown weighting coefficients and the unknown terms of the element matrices as
(47)
(48)
Thus, the element matrices are presented by the mixed-inverse method as follows
(49)
(50)
5. Results and discussion
The eigenvalues of the inverse and mixed-inverse formulations can be compared with those of the consistent and lumped formulations, as follows
(51)
(52)
From Equations (51) and (52) it can be seen that the inverse formulation yields the positive-semi-definite conductance and positive-definite capacitance matrices. shows that the eigenvalues of Ke obtained by the inverse method is greater than those obtained on the basis of the consistent method using the shape functions. In addition, the eigenvalues of Ce decreases from the lumped to mixed-inverse to inverse to consistent.
Figure 3. The eigenvalue λn versus the number of eigenvalue n (a) Ke and (b) Ce; (□) consistent; (○) lumped; (Δ) inverse; (∇) mixed-inverse.
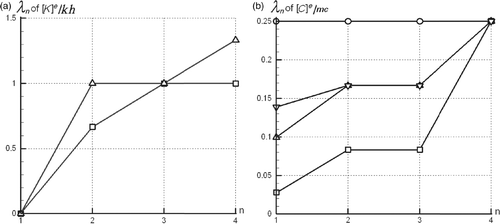
If the minimizing process of the discretization error is followed by the consistent and lumped formulations as that used for the inverse and mixed-inverse formulations, the orders of discretization error can be presented in , for all considered methodologies. It can be concluded that the discretization error in the inverse and mixed-inverse formulations is lower than lumped and consistent ones.
Table 1. The orders of discretization error for the considered methodologies.
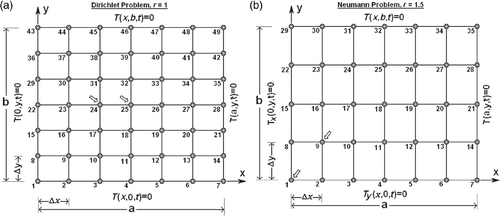
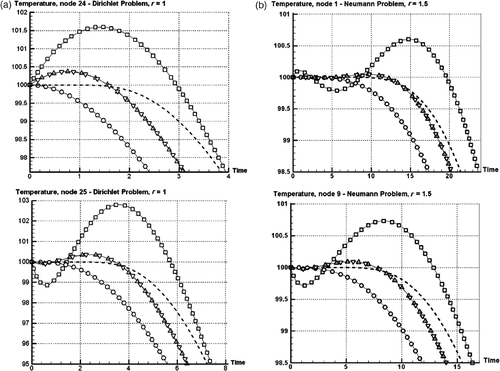
Herein, two illustrative problems are presented to show the validity and effectiveness of the new bilinear rectangular element matrices. Consider a rectangular plate in 0 ≤ x ≤ a and 0 ≤ y ≤ b, initially at temperature T0 = 100°C. The plate has the dimensions a = 6 cm and b = 6 cm, thickness h = 1 cm, thermal conductivity k = 2 w cm−1 °C−1, and heat capacity ρc = 20 J cm−3 °C−1. Let us now define a Dirichlet-type problem with square-mesh grids (r = 1) in case that the temperatures of all edges are kept at 0°C, as depicted in . A Neumann-type problem with rectangular-mesh grids (r = 1.5) is also defined by considering adiabatic boundaries for the edges x = 0 and y = 0 as well as zero temperatures for the edges x = a and y = b, as shown in . Assume that the domain of the Dirichlet and Neumann problems is divided into 36 and 24 bilinear rectangular elements, respectively. The analytical solution for the cases of Dirichlet and Neumann problems can be, respectively, obtained by the separation of variable method as follows
(53)
(54)
where α = k/ρc is the thermal diffusivity. After substituting the global form of the element matrices derived in Equations (36) and (38) as well as (49) and (50) into Equation (1) and using modal analysis, the solution of the system of ODEs (1) can be analytically obtained. shows the temperature distribution versus the time at nodes 24 (x = 2, y = 3) and 25 (x = 3, y = 3) for the Dirichlet problem and nodes 1 (x = 0, y = 0) and 9 (x = 1, y = 1.5) for the Neumann one. According to the physical law of the heat diffusion Citation17, the temperature diagram must ensure a monotonic solution in the time domain. It should be noted that the value of the initial temperature must continuously diminish for the transient solution process. Therefore, the finite element solution should not cause the temperatures to increase at internal nodes. Consequently, both the temperatures higher than the initial temperature and the oscillating outputs are unrealistic results and violate the physical reality. The results show that the violation of physical reality decreases from the consistent to inverse to mixed-inverse to lumped method. In other words, the inverse model applied to the bilinear rectangular element has a smaller error in comparison with the consistent formulation. Although the results obtained by the lumped formulation have no violation of the physical reality, it was shown in that its discretization error is large in comparison with the inverse and mixed-inverse formulations. Moreover, it will be demonstrated that the inverse and mixed-inverse formulations lead to more accurate eigenvalues for both Dirichlet and Neumann boundary conditions when compared with consistent and lumped formulations.
Figure 5. Temperature distribution versus time at nodes 24 and 25 of the Dirichlet problem and nodes 1 and 9 of the Neumann one; (□) consistent; (○) lumped; (Δ) inverse; (∇) mixed-inverse; (- - -) analytical.
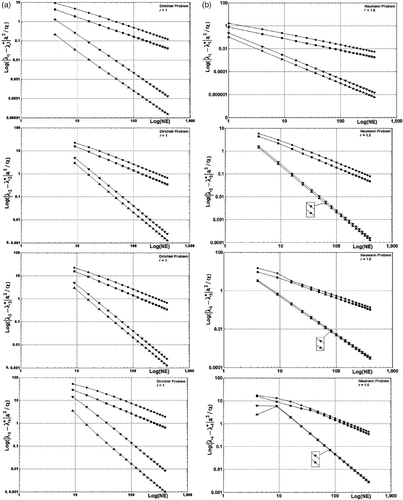
The normalized absolute value or indicating the difference between the eigenvalues of the analytical solution () and the finite element solution (λi) is defined as the measure of the error. shows the logarithm of the error for the first, second, third and fourth eigenvalues of the eigenproblem Kx = λCx versus the logarithm of the element numbers (NE) for the considered methodologies in both Dirichlet and Neumann cases. The amount of error in the inverse finite element formulation of the bilinear rectangular element is less than that in the other finite element formulations. The results of the error in the mixed-inverse formulation using the mixed capacitance matrix suggested by a few researchers Citation14–16,Citation18 lie between the consistent and inverse formulations. Furthermore, the inverse formulation as well as the mixed-inverse formulation have more rapid rate of convergence in comparison with the consistent and lumped formulations. It can be concluded that both inverse and mixed-inverse formulations presented in this article ensure highly accurate results and rapid convergence rate, as the number of elements increases. As a result, the element matrices established by the inverse formulation (Equations (36), (37) and (38)) are suggested by the authors for the two-dimensional finite element model of the diffusion problems.
5. Conclusions
In the present article, a new bilinear rectangular element model for diffusion problems was presented to minimize the discretization error in the element formulation by using the inverse method. With no use of the element shape functions, the element model in the inverse formulation was obtained in such a way that certain requirements are satisfied in its generic form; and a small discretization error is realized in its element formulation. Two types of boundary conditions are considered to validate the present formulation. This formulation yielded more accurate eigenvalues than the consistent and lumped formulations. Furthermore, the eigenvalues obtained by the inverse and mixed-inverse finite element models converge to the exact eigenvalues more rapidly than those obtained on the basis of the consistent and lumped ones. In addition, the violation of physical reality and unrealistic results are improved in the inverse finite element solution process when compared with the consistent one. Although the lumped formulation achieves the monotonic solution, its discretization error is higher than the inverse and mixed-inverse formulations. For the bilinear rectangular elements, when the inverse formulation is established by the linear combination of the lumped and consistent capacitance matrices, the accuracy of the mixed-inverse method lie between the accuracy of the consistent and inverse methods. Therefore, the inverse approach introduces a more accurate and useful model in a finite element formulation of the transient heat conduction problems.
References
- Rank, E, Katz, C, and Werner, H, 1983. On the importance of the discrete maximum principle in transient analysis using finite element methods, Int. J. Numer. Meth. Eng. 19 (1983), pp. 1771–1782.
- Ouyang, H, and Xiao, D, 1994. Criteria for eliminating oscillation in analysis of heat-conduction equation by finite-element method, Commun. Numer. Meth. Eng. 10 (1994), pp. 453–460.
- Thomas, HR, and Zhou, Z, 1998. An analysis of factors that govern the minimum time step size to be used in the finite element analysis of diffusion problems, Commun. Numer. Meth. Eng. 14 (1998), pp. 809–819.
- Mohtar, RH, and Segerlind, LJ, 1999. Dynamic time step and stability criteria comparison for the heat diffusion equation, Int. J. Therm. Sci. 38 (1999), pp. 475–480.
- Madoliat, R, and Ghasemi, A, 2007. Operating regions for discrete models based on physical reality of diffusion problems, J. Thermophys. Heat Transf. 21 (2007), pp. 158–165.
- Frey, S, Martins-Costa, ML, and Saldanha da Gama, RM, 1999. Stabilized finite element approximations for heat conduction in a 3-D plate with dominant thermal source, Comput. Mech. 24 (1999), pp. 118–126.
- Ilinca, F, and Hetu, J-F, 2002. Galerkin gradient least-squares formulations for transient conduction heat transfer, Comput. Meth. Appl. Mech. Eng. 191 (2002), pp. 3073–3097.
- Harari, I, Frey, S, and Franca, LP, 2002. A note on a recent study of stabilized finite element computations for heat conduction, Comput. Mech. 28 (2002), pp. 63–65.
- Harari, I, 2004. Stability of semidiscrete formulations for parabolic problems at small time steps, Comput. Meth. Appl. Mech. Eng. 193 (2004), pp. 1491–1516.
- Franca, LP, Ramalho, JVA, and Valentin, F, 2006. Enriched finite element methods for unsteady reaction–diffusion problems, Commun. Numer. Meth. Eng. 22 (2006), pp. 619–625.
- Franca, LP, Hauke, G, and Masud, A, 2006. Revisiting stabilized finite element methods for the advective–diffusive equation, Comput. Meth. Appl. Mech. Eng. 195 (2006), pp. 1560–1572.
- Ahmadian, H, Friswell, MI, and Mottershead, JE, 1998. Minimization of the discretization error in mass and conductance formulations by an inverse method, Int. J. Numer. Meth. Eng. 41 (1998), pp. 371–387.
- Madoliat, R, and Ghasemi, A, 2008. Inverse finite element formulations for transient heat conduction problems, Heat Mass Transfer 44 (5) (2008), pp. 569–577.
- Kim, K, 1992. A review of mass matrices for eigenproblems, Comput. Struct. 46 (1992), pp. 1041–1048.
- Hansson, PA, and Sandberg, G, 1997. Mass matrices by minimization of modal errors, Int. J. Numer. Meth. Eng. 40 (1997), pp. 4259–4271.
- Fried, I, and Leong, K, 2005. Superaccurate finite element eigenvalues via a Rayleigh quotient correction, J. Sound Vib. 288 (2005), pp. 375–386.
- Patankar, SV, 1980. Numerical Heat Transfer and Fluid Flow. New York: Hemisphere Publishing Corporation McGraw-Hill Book Company; 1980.
- Barauskas, R, 2003. Optimum mass matrices for short wave pulse propagation finite element models, Nonlinear Analy.: Modeling and Cont. 8 (2003), pp. 3–25.