Geared five-bar path generation with structural constraints

Abstract

The specific contribution made by this work in the area of geared five-bar path generation is the formulation of a non-linear optimization problem that includes elastic deflection, static torque and buckling constraints. Using this model, geared five-bar path generators are also synthesized with respect to static torque, deflection constraints and buckling constraints for a given rigid-body load.

Keywords:

• path generation
• geared five-bar mechanism
• torque
• deflection
• buckling

1. Introduction

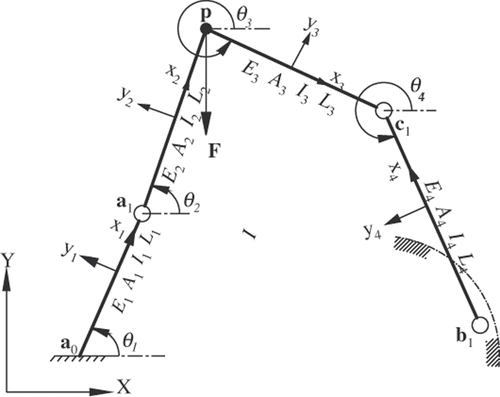
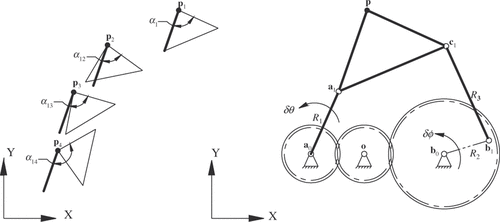
Mechanism synthesis is an inverse engineering field in which specific mechanism linkage dimensions are calculated to achieve or approximate a series of user-prescribed mechanism output parameters. In path generation (a subcategory of mechanism synthesis), the objective is to calculate the mechanism linkage dimensions required to achieve or approximate a set of prescribed rigid-body path points. This mechanism design objective is particularly useful when the rigid-body must achieve a specific path for effective operation (e.g. specific tool paths for accurate fabrication operations). In Figure 1, four sets of prescribed rigid-body path generation parameters are defined by variables p and α (prescribed path generation model input) and the model output are the calculated coordinates of the five-bar mechanism moving pivot variables a₁ and c₁ and scalar link lengths R₁ and R₃ required to approximate the prescribed path generation parameters. A conventional geared five-bar path generation model 1 is presented in the next section.

Figure 1. Prescribed rigid-body path generation parameters and calculated geared five-bar mechanism.

Path generation for planar five-bar mechanisms is a fairly-established field. Recent contributions include the works of Balli and Chand 2,3 that introduce a complex number method for the synthesis of a planar five-bar motion and path generator with prescribed timing and a method to synthesize a planar five-bar mechanism of variable topology type with transmission angle control. Mundoa et al. 4 performed an optimization of the five-bar linkage with non-circular gears as a mechanism capable of precisely moving a coupler point along a prescribed trajectory. Zhou and Ting 5 analysed singularity-free path generation capability of five-bar slider-crank parallel manipulators. Ge and Chen 6 introduced a software-based approach for the atlas method on path synthesis of geared five-bar mechanisms.

Although a substantial number of contributions have been made regarding planar five-bar path generation, the concept of including structural conditions in mechanism synthesis is not nearly as established. With the exception of Huang and Roth 7 whose work includes analytical synthesis models for planar four-bar mechanisms with a prescribed rigid-body load, most other works that investigate the structural behaviour of mechanisms under load do not consider the structural behaviour in the context of mechanism synthesis. The works of Dado 8, Venanzi et al. 9, Sönmez 10, Plaut et al. 11 and Sriram and Mruthyunjaya 12 do consider flexible links and/or buckling in mechanism design, but they consider the design of compliant mechanisms as opposed to classical linkage-based mechanisms.

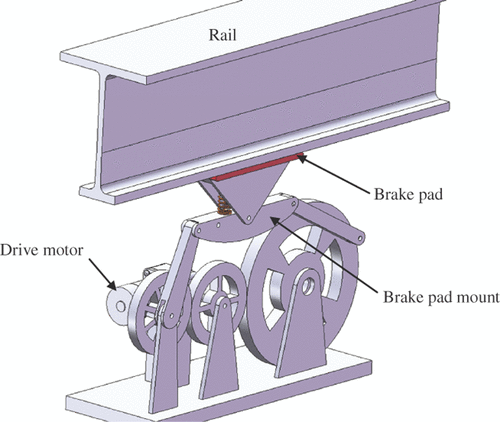
One application where a planar five-bar mechanism is subjected to rigid-body loads in static positions is braking. Figure 2 illustrates a five-bar traveller braking mechanism. This mechanism is used in suspension bridge travellers (a moving platform to carry personnel and equipment beneath suspension bridges for inspection and maintenance) when calliper brakes are not practical. When the brake is applied due to a driver torque (supplied by the drive motor in Figure 2), a reaction load is applied to the brake pad and subsequently the rigid-body. Other applications where a five-bar mechanism would be subjected to rigid-body loads in static or quasi-static positions include pressing, stamping and boring. Although the work of Huang and Roth 7 does consider planar mechanisms in static positions with rigid-body loads, this work does not consider link deflection and buckling due to the rigid-body loads-structural responses that will compromise the structural integrity of the mechanism and subsequently the accuracy of the precision points achieved.

Figure 2. Geared five-bar traveller braking mechanism.

The specific contribution made by this work regarding path generation with structural conditions for geared five-bar mechanism is the formulation of a non-linear optimization problem that includes elastic deflection, static torque and buckling constraints. Being a non-linear optimization problem, an indefinite number of prescribed rigid-body path points can be incorporated. As demonstrated in the included example, using the non-linear optimization problem formulated in this work, a geared five-bar mechanism is synthesized to approximate a set of prescribed rigid-body path points and also satisfy specified elastic deflection, static torque and buckling conditions for a given rigid-body load.

2. Geared five-bar path generation

Equations (1–3(1) ) encompass a conventional geared five-bar motion generation model 1. (1) (2) (3)

These equations are ‘constant length’ constraints and ensure the fixed lengths of links a₀a₁, b₀b₁ and b₁c₁ throughout the prescribed rigid-body displacements. Variables and in Equations (1–3(1) ) are the prescribed squared scalar lengths of links a₀a₁, b₀b₁ and b₁c₁ respectively. Variables R₁, R₂ and R₃ are interchangeable with , and . (4) (5)

Equation (4(4) ) is a rigid-body planar displacement matrix. Equation (5(5) ) is the angular displacement matrix for link b₀b₁ where and (δφ)_1i = k(δθ)_1i. Variable k represents the gear ratio of the gear train joining grounded links a₀a₁ and b₀b₁. From this conventional planar five-bar path generator model, 12 of the 13 unknown five-bar mechanism variables a₀, a₁ R₁, b₀, b₁, R₂, c₁ and R₃ are calculated with one arbitrary choice of parameter for five sets of prescribed rigid-body path generation parameters (where a₀ = [a_0x, a_0y, 1], a₁ = [a_1x, a_1y, 1], b₀ = [b_0x, b_0y, 1], b₁ = [b_1x, b_1y, 1] and c₁ = [c_1x, c_1y, 1]). If R₁, R₂ and R₃ are replaced with a₀, a₁, b₀, b₁ and c₁, then nine of the 10 unknown five-bar mechanism variables are calculated.

3. Geared five-bar mechanism under rigid-body load

In this work, the moving pivot b₁ is affixed to the gear centred at the fixed pivot b₀ (Figure 1). The moving pivot does not extend beyond the pitch circle. Also, the gears are considered rigid and subsequently not subject to deflection due to rigid-body loading.

Figure 3 illustrates a statically-loaded geared five-bar mechanism deflection model diagram. In this work, link a₀a₁ is only connected to its corresponding gear at a₀. Because of this condition, link a₀a₁ is illustrated in Figure 3 as having a single connection to the ground. A load {F} is applied to the mechanism (in this work, at rigid-body point p). An analytical model to calculate the deflections {U} at any element node on this mechanism is formulated using Equation (6(6) ) where the 15 × 15 global stiffness matrix [K_gobal] for the mechanism is composed of Equation (7(7) )–the element stiffness matrix for each mechanism link. The element stiffness matrix for link a₀a₁ and the rigid-body (link a₁pc₁) is given by Equation (8(8) ) 13. Because link b₁c₁ is a two-force member (and therefore under columnar loading only), its element stiffness matrix [k_axial] is given by Equation (9(9) ) 13. Equation (10(10) ) transforms each local element coordinate frame to the global coordinate frame by rotating each element node by the associated element angle θ_j 13.

Figure 3. Statically-loaded geared five-bar deflection model diagram mechanism.

In Figure 3 variables E_j, A_j, I_j and L_j (where j = 1, 2, 3, 4) are the modulus of elasticity, cross-sectional area, moment of inertia and length of each link, respectively. Because link a₁pc₁ is to be a uniform rigid-body in this study, E₂ = E₃, A₂ = A₃, I₂ = I₃ and its modulus of elasticity is one million times higher than those of link a₀a₁ and link b₁c₁ (specifying such a large modulus makes the coupler link virtually rigid). The angular orientation of each link (using the positive x-axis as reference) is denoted by angle θ_j (where j = 1, 2, 3, 4). These angles are used in the transformation matrix (Equation (10(10) )). (6) (7) (8) (9) (10)

4. Driver static torque constraint

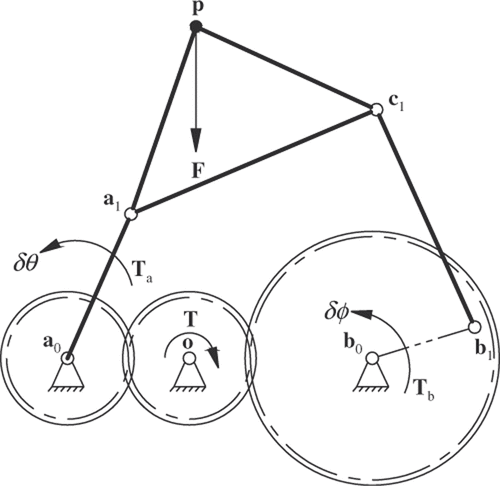
With an external load F acting on the rigid-body of the geared five-bar mechanism, a torque T applied to the driver (which is the intermediate gear in this work) achieves static equilibrium. In Figure 4, the load F is applied to rigid-body at point p. To formulate the driver static torque constraint, the moment condition ΣM = 0 (Figure 5b) is taken about the fixed pivot a₁. The equilibrium moments equation about the fixed pivot a₁ is (11) where (12)

Figure 4. Geared five-bar mechanism in static equilibrium.

The reaction load R_c is a real number that varies with the mechanism position. Equation (12(12) ) is the product of the columnar load along link b₁c₁ (R_c) and the unit vector for link b₁c_1. Solving for R_c from Equations (11(11) ) and (12(12) ) and substituting it in Equation (11(11) ) we get R_c1 as (13)

Figure 5. Geared five-bar mechanism link a₀a₁ (a) rigid-body (b) and link b₀b₁ (c) in static equilibrium with reaction loads R_a1 and R_c1.

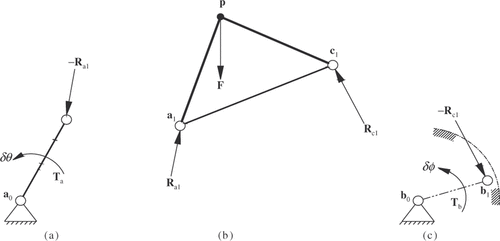
The resulting equilibrium of force equation for the rigid-body in Figure 5(b) is (14)

Substituting Equation (13(13) ) into Equation (14(14) ) and solving for R_a1 produces (15)

With the rigid-body reaction load Equations (13(13) ) and (15(15) ) formulated, torque equations for the gears about a₀ and b₀ are formulated next. The moment condition ΣM = 0 is taken about the fixed pivot a₀ for link a₀a₁ in Figure 5(a). The resulting equilibrium equation of the moments about a₀ is (16)

Substituting Equation (15(15) ) into Equation (16(16) ) and solving for torque T_a produces (17)

The moment condition ΣM = 0 is now taken about the fixed pivot b₀ for link b₀b₁ in Figure 5(c). The resulting equilibrium equation of the moments about b₀ is (18)

Substituting Equation (13(13) ) into Equation (18(18) ) and solving for torque T_b produces (19)

In Equations (17(17) ) and (19(19) )

As mentioned earlier, the intermediate gear is the designated driver in this work. Neglecting power loss, the static equilibrium driver torque is (20) where . Variables r_a, r_b and r are the pitch radii of the gears centred at a₀, b₀, and o, respectively (Figure 4). Equation (20(20) ) calculates the five-bar mechanism driver static torque for a given rigid-body load. Expressing Equation (20(20) ) as an inequality constraint to limit the maximum driver static torque for N prescribed rigid-body path points yields (21)

5. Link buckling and elastic deflection constraints

As previously discussed, link b₁c₁ is under columnar loading only because it is a two-force member. The Euler formula for critical buckling load for a column with pinned ends 14 is (22) where variables E, I and L are the modulus of elasticity, moment of inertia and effective column length, respectively. The equation for scalar columnar load R_c in link b₁c₁ is formulated by substituting Equation (12(12) ) into Equation (11(11) ) and solving for R_c. Expressing Equation (3(3) ) as an inequality constraint to prevent link b₁c₁ buckling for N the prescribed rigid-body path points yields (23) where the right-side term is L² in Equation (22(22) ). Because the right-side term in inequality constraint (23) is the squared scalar length of link b₁c₁, this link is constrained to a length that is less than its buckling length.

Unlike link b₁c₁, link a₀a₁ is not a two-force member and subsequently not under columnar loading only. Because this link is held in static equilibrium by a torque about a₀, there is also a transverse load component acting on link a₀a₁. In this work, the buckling of link a₀a₁ is not explicitly considered because the link stiffness required to limit transverse deflection is generally sufficient in avoiding link buckling (especially as the maximum permissible transverse deflection becomes smaller). As shown in Figures 3 and 5(a), this link is a fixed-end cantilevered beam under a load with a transverse component. Because the constraint and loading conditions on link a₀a₁ make link deflection a common occurrence, constraining the deflection of link a₀a₁ is critical.

The Euler formula for the deflection of a fixed-end cantilevered beam 14 is (24) where variables P, L, E and I are the free-end transverse load, beam length, modulus of elasticity and moment of inertia, respectively. Equation (15(15) ) is the total load on the moving pivot a₁. The transverse component of this load is (25)

Expressing Equation (1(1) ) as an inequality constraint to limit crank deflection for N the prescribed rigid-body path points yields (26) where the right-side term is L² in Equation (24(24) ). Because the right-side term in inequality constraint (26) is the squared scalar length of link a₀a₁, this link is constrained to a length that produces a maximum static deflection that is less than the specified maximum static deflection.

6. Path generation non-linear optimization problem

Formulating Equations (1(1) ) and (3(3) ) into a single objective function that accommodates an indefinite number of N sets of prescribed path generation parameters to be minimized yields (27) where . Equation (27(27) ) and inequality constraints (21), (23) and (26) constitute a non-linear optimization problem from which mechanism solutions that approximate the prescribed rigid-body path points and satisfy maximum static torque, maximum elastic deflection and buckling conditions are calculated.

The algorithm employed for solving this non-linear optimization problem (a non-linear constraints problem) is sequential quadratic programming (SQP) which uses quasi-Newton approach to solve its quadratic programming (QP) subproblem and line search approach to determine iteration step. The merit function used by Han 15 and Powell 16 is used in the following form: (28) where represents each inequality constraint, m is the total number of inequality constraints and the inequality constraint penalty parameter is (29)

The value of r for successive minimizations can be found as (30) where IR at the start and is incremented by 1 after each successive suboptimum is found. The factor FAC can be set arbitrarily although 10 is suggested for normal use 1. In Equation (30(30) ) l is the iteration index for calculating the penalty parameter for each inequality constraint (l = 0, 1, 2, 3, …). The Lagrange multiplier, which is the rate of the change of the objective function being optimized with respect to the constraint variables, is (31)

After specifying initial guesses for the unknown variables in the non-linear optimization problem (X), the following SQP steps were employed to calculate the unknown variables:

1.	calculate and , (where l = 0 and k = 1, …, m)
2.	solve Equation (28(28) ) using quasi-Newton method
3.	calculate using Equation (29(29) ) (where l = l + 1 and k = 1, …, m)
4.	repeat step 2 with newly-calculated .

Steps 2–4 constitute a loop that is repeated until the penalty term in Equation (28(28) ), is less than a specified penalty term residual (which is 0.001 for the example in this work).

The SQP algorithm does not guarantee global optimization. The quality of the initial guesses could determine whether or not the algorithm converges (or if it does converge, to what values). The authors employed computer-aided drafting software to assist in specifying the initial guesses. Drafting and superimposing the prescribed rigid-body precision positions in 2-D space enabled the authors to determine likely locations (and subsequently likely initial guesses) for the fixed and moving pivots.

Rather than codifying the SQP algorithm as a stand-alone program, the authors used Mathcad–a commercial mathematical analysis software with SQP built in. Other commercial mathematical analysis software such as Mathematica and Matlab also include non-linear optimization problem solvers like SQP. The non-linear optimization problem formulated and presented in this work ran efficiently in Mathcad–having run times that measured in seconds.

7. Example

Table 1 includes the x- and y-coordinates (in inches) of eight prescribed rigid-body path points and displacement angles (therefore N = 8 in Equation (27(27) )). This is nearly twice the maximum number of prescribed path points available with the conventional path generation method included in this work 1. The maximum allowed driver torque is τ_max = 6350 in-lbs and the rigid-body load at p is F = (0, −1000, 0)^T lbs with gear pitch radii r_a, r_b and r of 5, 10 and 5 inches, respectively. Link a₀a₁ and b₁c₁ shall be constructed of solid rectangular steel tubing (E = 29 × 10⁶ psi) of ¾ in (deep) × ½ in (wide) and 9/32 in × ¼ in, respectively. This example assumes that the links will be constructed of ‘off-the shelf’ steel bars of standard sizes (as opposed to custom made bars where the moment of inertia could be a design variable). For each prescribed rigid-body position, the maximum deflection of link a₀a₁ shall not exceed 0.31 inch and preventing the buckling of link b₁c₁ is critical.

Table 1. Prescribed rigid-body path generation parameters.

	pPrescribed (in)	αPrescribed (°)
Pos 1	12.6931, 14.5459	0
Pos 2	11.8060, 15.9834	−1.0796
Pos 3	8.8795, 17.6313	−4.5053
Pos 4	6.3575, 17.6999	−6.2497
Pos 5	3.0503, 16.6618	−5.1847
Pos 6	−0.4948, 14.1519	−2.6701
Pos 7	−3.0512, 10.9525	15.9055
Pos 8	−4.3877, 6.2947	30.4887

Using the path generation non-linear optimization problem (where N = 8 results in m = 24 in Equation (28(28) )) with prescribed values (in inches) of a₀ = (0, 0), b₀ = (25, 0), b₁ = 33, 6) and R₂ = 10, and initial guesses (in inches) of a₁ = (10, 5), R₁ = 10, c₁ = (20, 20) and R₃ = 15 the calculated solution is a₁ = (6.9002, 4.2070), R₁ = 8.0815, c₁ = 22.3731, 17.9572) and R₃ = 15.9274. Table 2 includes the resulting static torque and deflection of the crank link as well as the resulting columnar loads for link b₁c₁. Using Equation (22(22) ), the calculated critical buckling load for link b₁c₁ for the synthesized mechanism is 411 pounds. The length required to satisfy the transverse deflection condition for link a₀a₁ also results in safe buckling load of 78,612 pounds.

Table 2. Crank static torques, deflections and follower link columnar loads.

	Crank static torque (in-lb)	Crank deflection (in)	Follower-link load (lbf)
Pos 1	6086	0.2023	270
Pos 2	4658	0.1352	299
Pos 3	1327	0.0126	335
Pos 4	1067	0.1166	354
Pos 5	3703	0.2305	373
Pos 6	5727	0.3084	355
Pos 7	6339	0.3097	274
Pos 8	5242	0.2310	75

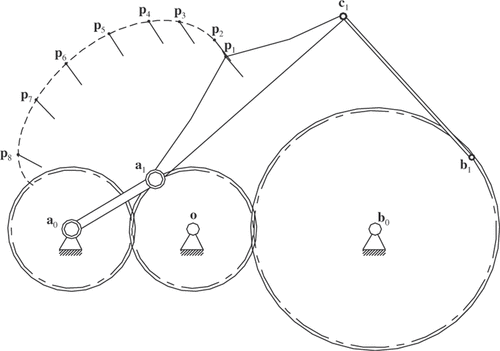
Because links a₀a₁ and b₁c₁ are flexible, the deflections of these links simultaneously compromise the accuracy of the rigid-body path points achieved by the synthesized mechanism. Table 3 includes the rigid-body path points (and corresponding angles for link a₀a₁) calculated after incorporating the parameters of the synthesized mechanism in the geared five-bar mechanism deflection model in Section 3. Table 3 also includes the scalar difference between the achieved and prescribed rigid-body path points. Figure 6 illustrates the synthesized geared five-bar path generator. As illustrated in this figure, the moving pivot b₁ is on the pitch circle of the gear centred at the fixed pivot b₀.

Figure 6. Synthesized geared five-bar path generator.

Table 3. Rigid-body path points achieved by synthesized elastic geared five-bar mechanism, crank angle and precision point scalar structural error |p_Prescribed − p_Achieved|.

	Driver angle, θ1 (°)	pAchieved (in)	|pPrescribed − pAchieved| (in)
Pos 1	31.3702	12.6865, 14.4296	0.1165
Pos 2	46.3962	11.7291, 15.9050	0.1098
Pos 3	75.3991	8.8854, 17.4951	0.1363
Pos 4	95.2591	6.4339, 17.4962	0.2176
Pos 5	119.9135	3.2257, 16.3313	0.3742
Pos 6	149.7264	−0.5949, 13.6911	0.4715
Pos 7	178.2751	−2.9873, 10.6270	0.3317
Pos 8	222.5464	−4.3624, 6.1295	0.1671

Using the conventional path generation model with initial guesses (in inches) of a₀ = (0, 0), a₁ = (10, 5), b₀ = (25, 0), b₁ = (33, 6) and c₁ = (20, 20), the calculated solution is a₀ = (5.1549, 3.6340), a₁ = (11.6178, 8.0042), b₀ = (9.5497, −0.3464), b₁ = (31.2905, 4.7351, and c₁ = (10.9531, 11.5631). This five-bar mechanism solution has a b₁c₁ length of R₃ = 21.4530 which is 34.69% longer (and more susceptible to buckling with a critical buckling load of just 227 pounds).

8. Discussion

The non-linear optimization problem presented in this work does not consider the load contribution made by the link masses because the five-bar mechanism is assumed to be static and the rigid-body loads considered are assumed to far exceed the link body forces. Planar five-bar applications as such are best suited for this methodology. Equations (17(17) ), (19(19) ) and subsequently (20) become invalid when the pivots a₁, b₁ and c₁ are collinear. Such a state is possible when the five-bar mechanism reaches a ‘lock-up’ or binding position. When pivots a₁, b₁ and c₁ are collinear, the denominator in Equations (17(17) ) and (19(19) ) become zero (making these equations and subsequent driver torque constraint invalid). The specific geared five-bar mechanism design considered in this work is one where a₀a₁ is a link attached to the gear centred at a₀ and b₁ is a moving pivot on the gear centred at b₀. If the moving pivot a₁ is to be mounted directly to the gear centred at a₀, the deflection constraint (Equation (26(26) )) can be excluded from the non-linear optimization problem since the gears are considered rigid. Different types of gear-to-link attachments change the mechanism elastic behaviour (Equation (5(5) )) and subsequent deflection constraints (Equation (26(26) )). The mathematical analysis software MathCAD was used to codify and solve the formulated goal program.

9. Conclusion

A non-linear optimization problem to synthesize geared five-bar path generators that also includes static torque, elastic deflection and buckling constraints was formulated and demonstrated in this work. Given a set of rigid-body path points, a rigid-body load, maximum driver torque and deflection values and Young's modulus and moment of inertia data for links a₀a₁ and b₁c₁, a geared five-bar mechanism was synthesized using the non-linear optimization problem formulated in this work.