A method for identifying a spacewise-dependent heat source under stochastic noise interference

Abstract

We consider an inverse problem of determining a spacewise-dependent heat source in the time-dependent heat equation using the usual conditions of the direct problem and information from temperature measurements at a given single instant of time. This spacewise-dependent temperature measurement ensures that the inverse problem has a unique solution, but the solution is unstable and hence the problem is ill-posed. Furthermore, it is assumed that information about this temperature measurement is available only at a finite number of points, and moreover, these measurements are blurred by a stochastic noise. The continuous problem is discretized using a finite element method and for the discrete model an estimate of the heat source is obtained by a Tikhonov regularization. It is proved that increasing the number of measurements and decreasing the mesh size produces a sequence of solutions which under appropriate conditions converge to the continuous heat source.

Keywords:

• finite element method
• heat source
• inverse problem
• parabolic heat equation
• stochastic noise
• Tikhonov regularization

AMS Subject Classifications::

• Primary: 35R25
• Secondary: 35K05

1. Introduction

When solving applied engineering problems, there is usually a certain amount of uncertainty involved, for example, the material coefficients are known only up to some accuracy or through random external influences. Furthermore, the model is usually of the form that the solution does not depend continuously on the data, i.e. the problem is ill-posed. In this article, we study one such model having these properties, i.e. being both ill-posed and stochastic. This model is described below.

We consider the problem of source identification from measured data for the time-dependent heat equation. There are several important applications of such a model, for example, in finding a pollution source intensity, given measurements of the pollutant concentrations at a later time and also for designing the final state in melting and freezing processes.

Assume that we have a non-homogeneous and non-isotropic body, denoted by Ω, occupying a bounded domain in Rⁿ, where n ≥ 1. For simplicity, assume that the temperature is zero on the boundary Γ of Ω. Then the temperature u, heat source f(x) and the initial temperature ϕ(x) satisfy (1) where T > 0. Here, L is a linear elliptic operator of the second-order with time-independent smooth coefficients. A possible expression for L is Lu = −∇ · (k(x)∇u), where k > 0 is the thermal conductivity of the body. Using linearity, one can also consider the case of a non-homogenous Dirichlet boundary condition. Moreover, the ideas presented can, in principle, be applied to other types of boundary conditions and to operators L with non-smooth coefficients corresponding to, for example, layered materials.

In inverse problems it is of importance to specify appropriate data so that the parameter to be reconstructed is uniquely identifiable. In our model, this will be assured by using information about the solution obtained from a spacewise temperature measurement at a later instant of time. This type of inverse problem of determining an unknown inhomogeneous spacewise-dependent heat source function in the parabolic heat equation has mainly been considered in a few theoretical papers concerned with the existence and uniqueness of the solution, notably in 1–3. Recently (see, e.g. 4), an iterative procedure, using these rigorous mathematical conditions, was proposed and analysed for finding the source given the additional information (2) Let us mention that the problem of determining ϕ from the spacewise-dependent temperature measurement (2), given that f = 0, i.e. the backward heat conduction problem, has been studied extensively (see, e.g. 5,6).

In most of the practical applications, however, only a finite amount of data is available. In this work, we will therefore assume that there are N noisy measurements U_i of the temperature u at time T > 0 at (random) points X_i described by an inverse regression model (3) Here, (X_i, ϵ_i) are independent and identically distributed random variables and further requirements on these variables will be imposed below. The function v describes the conditional variance of the measurement errors, and if v is constant the model is called homoscedastic, otherwise is heteroscedastic. We point out that for the method constructed in this article no a priori information is required on the noise level, i.e. the method is fully data driven. We also mention that similar results hold in the case of a deterministic design model, i.e. when the points X_i are known and fixed. Moreover, we apply a frequentist's approach and do not invoke Bayesian statistics in this work. For different concepts of probability that can be incorporated, for example, belief and plausibility, see the introduction in 7. Also note that we consider the coefficients of the operator L, the domain Ω and the initial data ϕ as fixed, i.e. not stochastical.

An outline of this article is as follows. In Section 2 we introduce some additional assumptions and notations, and review some facts about the direct and inverse source problems. In order to overcome the instability of the solution to (1–2), we consider u(x, T), where u solves (1), as a control that has to be determined to satisfy (2). For the construction of the function f, we wish to minimize a functional relating the discrepancy between the known and the calculated values on Ω × {T}. In Section 3, we review some results for this functional proved in 8, for example, it is twice Fréchet differentiable. We further show that the functional is weakly continuous (Lemma 3.2). For practical applications, we discretize the source problem using a finite element method (FEM), see Section 4, and prove in Theorem 4.2 that the solution of the discretized minimization tends to the solution of the continuous one. Then, in Section 5, we consider the case where instead of (2) we have only finite amount of data of the form (3). A method for obtaining an approximation of the heat source is proposed in the beginning of Section 5. In the first step of this method, an estimate of ψ is obtained from the measurements (3) using a local polynomial estimator, and then this estimate is used in our discretized model to obtain an approximation to the heat source using stochastic Tikhonov regularization. Employing recent results about the stochastical properties of this approach 9, we show that increasing the number of measurements and decreasing the mesh size produce a sequence of solutions which is a minimizing sequence for the continuous discrepancy functional (Theorem 5.2). In Section 6, we present some numerical results based on the proposed procedure. From these results it can seen that it is possible to obtain an accurate reconstruction of the heat source. Finally, in Section 7, we present some conclusions.

2. Solvability for the direct and inverse problems

2.1. Functional spaces

Let Ω be a bounded domain of Rⁿ, where n ≥ 1, with Lipschitz boundary ∂Ω = Γ. The space L²(Ω) consists of square integrable functions on the domain Ω with the usual norm ‖ · ‖_L²(Ω) and scalar product (·, ·). As usual, the space H^k(Ω), where k = 1, 2, …, denotes the standard Sobolev space on Ω, i.e. the space of functions with generalized derivatives of order ≤ k in L²(Ω). Since the boundary of Ω is Lipschitz, the trace of functions in H¹(Ω) to the boundary is well-defined and consists of functions in H¹(Ω) with u|_Γ = 0.

Let T > 0 be a fixed number. The space L²(0, T; X), where X is a Hilbert space, denotes the space of measurable functions u(·, t) : (0, T) → X, such that By C([0, T]; X), we mean functions u such that u(·, t) : [0, T] → X is continuous (in the usual norm).

Let (Ω_𝒫, ℱ, 𝒫) be a complete probability space, where Ω_𝒫 is the set of outcomes and ℱ is a σ-algebra of events and 𝒫 is a probability measure (𝒫 : ℱ → [0, 1]). Assume that Y is an R^d-valued random variable in (Ω_𝒫, ℱ, 𝒫), which is in L¹(Ω_𝒫). By E[Y] we denote the expected value of Y, i.e. E[Y] = ∫_Ω𝒫Y(ω)dP(ω), and, when defined, the variance is Var[X] = E[(X − E[X])²].

For the random variables in (3), it is assumed that E[ϵ_i|X_i] = 0 and . Moreover, E[Y_i|X_i] = ψ(X_i) and for the variance Var [Y_i|X_i] = v(x_i), where the function v ∈ L²(Ω_𝒫). The random variables X_i have values in Ω distributed according to a common, but unknown design density f_Ω𝒫.

2.2. The differential operator L

Let (4) where a_i,j = a_j,i and a_i,j, and . We suppose that this operator L is elliptic, i.e. there exists a constant C such that Since we can always change u into e^λtu, the coefficients are assumed chosen such that there exists a constant C > 0 with (5) for all and λ ≥ 0, where Given these conditions, the operator −L generates a C₀ (continuous) contraction semigroup {G(t)}_t∈R⁺ in L²(Ω) with a dense set of its domain (see, e.g. 10). Moreover, −L is strictly dissipative and hence (6)

The space can be compactly embedded into L²(Ω), which implies that G(t) is a compact operator for every t > 0. We point out that the above results hold under weaker assumptions on the coefficients, for example, the coefficients can be piecewise smooth, corresponding to a layered material.

As a direct consequence of the fact that −L generates a semigroup, we have the following solvability result due to [11, Chapter 3].

LEMMA 2.1

Suppose that the initial temperature ϕ and the heat source f are given in L²(Ω). Then (1) has a unique solution in the distributional sense and (7)

Note that the homogeneous Dirichlet boundary condition in (1) is satisfied since the solution belongs to the space .

2.3. Solvability of the inverse problem (1–2)

We only consider the case of strong solutions, and therefore assume that and that the heat source f is sought in L²(Ω). The set of admissable temperatures consists of functions u with (8) Exploring the fact that the operator −L generates a contraction semigroup and condition (6), we have the following result due to [2, Theorem 1].

THEOREM 2.2

Let , then the inverse problem (1–2) has a unique solution among heat sources f ∈ L²(Ω) and temperatures u that satisfy (8).

This result can be extended to include weaker assumptions on the data, but then one has to consider an appropriate weak formulation of (1–2). In Lemma 3.1 in 8 it was shown that there exists a solution for all sources belonging to a dense set of L²(Ω). As was pointed out in 8,12, the assumption that both ‖ϕ‖_H¹(Ω), ‖ψ‖_H¹(Ω) → 0 is not sufficient to guarantee the stability of the heat source f.

3. A discrepancy functional and some of its properties

Let the operator A : L²(Ω) → L²(Ω) be defined by (9) where u is the unique (weak) solution to (1) with heat source f(x) = g(x), guaranteed by Lemma 2.1. This operator is well-defined and bounded according to Lemma 2.1, not linear (unless ϕ = 0) but affine linear. From [8, Section 3.1] Equation (9) has a unique solution and the range of A is dense in L²(Ω). To construct a solution to (1–2), we shall minimize the (quadratic) functional (10) with respect to sources g ∈ L²(Ω). The following result is the content of Theorem 3.2 in 8.

THEOREM 3.1

The functional J given by (10) is twice Fréchet differentiable and strictly convex. The gradient of J is given by (11) where v is the weak solution to (12) with ζ = 0 and g = u(x, T) − ψ_T, and

In the proof of this theorem given in 8, the following estimate is shown: (13) where u_h is a solution to (1) with f = h and ϕ = 0.

The next lemma is needed for the convergence of the regularizing method that we develop to reconstruct the heat source.

LEMMA 3.2

The functional J defined in (10) is weakly continuous.

Proof

Let f_k be a sequence in L²(Ω) that converges weakly in L²(Ω) to a function f ∈ L²(Ω). Denote by u_k the solution of the boundary value problem (1) with the source data f = f_k. Then from the definition of a weak solution in we have for every . Since f_k converges to f weakly, the right-hand side tends to zero when k → ∞. Therefore, This and the inequality (5) imply that u_k(·, t) converges weakly to u(·, t) in the norm for t ∈ (0, T]. Combining this with the compact imbedding of into L²(Ω) gives, in particular, that u_k(·, T) converges strongly to u(·, T) in L²(Ω). Now, using the definition of the functional J in (10) implies that J(g_k) converges to J(g).

Since the domain of A is closed and convex and by the Lemma 3.2 A is weakly continuous, we conclude by giving the following lemma.

LEMMA 3.3

The operator A in (9) is weakly closed.

4. A discretized version of the minimization problem

In this section, we introduce a discretization of the functional J in (10) using a FEM. We prove that the minimum to this discretized problem tends to the minimum of the continuous one as the mesh size tends to zero.

4.1. Some further assumptions and FEM spaces

For simplicity, to avoid singularities in the solution, we assume that Ω is a convex polyhedral domain. There are several different FEM's for parabolic equations, for an overview see, 13. In principle, any FEM can be applied for the discretization in the next section. For the sake of completeness, we outline one possible FEM in this section.

Let be a family of finite element approximation spaces consisting of piecewise linear continuous functions on conforming (non-degenerate) triangulations, τ_hx, of the domain, Ω, with a maximum mesh spacing parameter h_x > 0. Standard approximation estimates then hold for these finite element spaces, e.g. (14) where C is independent of both the function u and the mesh size h_x. By P_hx we denote the projection of L²(Ω) onto X_hx, defined (on H¹(Ω)) by Note that P_hx is not necessarily symmetric, but due to (5) it is positive definite on the space X_hx. Let be a finite sequence of numbers with t₀ = 0 and t_M = T, and maximum time-step size h_t. We consider the finite element space T_ht of (discontinuous) piecewise polynomials with degree ≤ 1 on each interval (t_m, t_m+1), m = 0, 1, …, M − 1. This space has the similar approximation property as (14), namely (15) We define the tensor space V_hx,ht = X_hx ⊗ T_ht. Let u be a solution to (1) and ϕ_hx = P_hx ϕ. The finite element approximation u_hx,ht ∈ V_hx,ht of u can then be defined as the element in V_hx,ht with u_hx,ht(x, 0) = ϕ_hx(x) and (16) for every v ∈ V_hx,ht and m = 0, 1, …, M − 1. Here, v⁺⁽⁻⁾(·, t_m) = lim_{s→0⁺⁽⁻⁾}v(·, t_m + s). It is a standard fact that u_hx,ht exists and is unique (see, e.g. 13).

4.2. The discretized functional J and some of its properties

Let ϕ_hx = P_hxϕ and P_hxψ = ψ_hx, where P_hx is the operator defined in the previous section mapping into the space X_hx.

Let be the weak solution to (1) guaranteed by Lemma 2.1. Let S_hx be the image of L²(Ω) under the projection P_hx and introduce the operator A_hx,ht : S_hx → V_hx,ht by (17) where u_hx,ht ∈ V_hx,ht is the (unique) Galerkin approximation of the weak solution u with initial data ϕ_hx, constructed in the previous section. From the properties shown for the operator A in Section 3 we note, in particular, that A_hx,ht is weakly closed and that the equation (18) has a solution in S_hx. To construct a solution let (19) where f ∈ S_hx. From Theorem 3.1 it follows that also J_hx,ht is twice Fréchet differentiable and one can find an expression for its derivative that will involve the corresponding Galerkin approximation of (12).

Denote by J* and the minimum of the functionals J and J_hx,ht, respectively.

LEMMA 4.1

Given a tolerance δ > 0, there is a number h_δ > 0 such that for max{h_x, h_t} < h_δ and f ∈ L²(Ω) (20)

Proof

From the definition of the functionals J and J_hx,ht we have (21) Applying the triangle inequality to the expression on the right-hand side of (21), one obtains (22) Due to the homogeneous boundary condition and the smoothness of ψ it follows that u is sufficiently smooth near t = T, so standard Galerkin error estimates can be applied showing that the right-hand side of (22) tends to zero as max{h_x, h_t} tends to zero.

We can construct a sequence f_hxj,htj, j = 1, 2, …, such that {h_xj, h_tj} tends to zero as j tends to infinity and (23) with → 0 as j → ∞. We can then show the following theorem from [14, Theorem 6].

THEOREM 4.2

For a given tolerance δ > 0, by choosing max{h_x, h_t} sufficiently small, we have

Proof

Given a δ > 0, there exists an element f_δ such that (24) According to Lemma 4.1 we can choose h so small that Combining this with (24) we conclude that for max{h_x, h_t} sufficiently small (25) Conversely, we also find that for max{h_x, h_t} sufficiently small (26) Then, employing the sequence in (23), we obtain (27) The first term on the right-hand side of (27) tends to zero according to Lemma 4.1, the second term tends to zero from the construction of and the last term tends to zero from the first part of the proof. The proof is thus complete.

Remark

Using the estimate (22) and standard Galerkin approximation estimates, it is possible to explicitly establish how to choose h_x and h_t so that the first and third term on the right-hand side in (27), each are less than δ/3. For the second term on the right-hand side in (27), one can undertake an analysis based on the singular value decomposition to control its size.

5. Minimization of the discrete functional (19)

From now on, we assume that data is chosen so that there exists a source solution to the inverse problem (1–2), and that the design density (for X_i) is in . Then, to minimize, in a stable way, the non-linear functional J_hx,ht defined in (19), we can apply a recent Tikhonov regularization method described in 9. We assume that we only have access to a finite number N of measurements of the function ψ of the form (3). The method we propose and investigate is the following:

1.	Obtain an estimate of ψ.
2.	Construct the Galerkin approximation of .
3.	Substitute for in (19) and minimize , where αN > 0 is the regularization parameter and f0 is a guess of the actual source.

We shall show that we can obtain a minimizing sequence to (10) by using the above method, where the number of measurements is increasing and the mesh size decreasing. For this, we choose a specific estimate of ψ such that (28) where β_N is a sequence of real numbers tending to zero when the number of observations N tends to infinity. To construct this estimate from (3) one can, for example, use a local linear polynomial estimator 9, Section 4].

Let be the Galerkin approximation of . We note that (28) implies that also (29) Now, let be a minimizer of (30) where is in S_h and and let be a minimizer of (19). Since the operator A_hx,ht is weakly closed, the following result is a consequence of [9, Theorem 2].

LEMMA 5.1

There exists a sequence of regularizing parameters α = α_N, N = 1, 2, …, such that (31) as N → ∞.

Remark

The regularizing parameters in Lemma 5.1 can be estimated by a priori methods 9, Section 3].

We can then prove the following result.

THEOREM 5.2

Given a tolerance δ > 0, one can find h_x, h_t and an integer N such that (32)

Proof

Note that by definition . From (27) we find (33) We can choose the mesh size so that the first and third term on the left-hand side each is less than δ/3 according to Lemma 4.1 and Theorem 4.2, respectively, and by Lemma 5.1 we can then choose N so that the second term is also less than δ/3.

We can then construct a sequence with as δ → 0. Since, according to Lemma 3.2, the functional J is weakly continuous we can conclude that also converges weakly.

We remark that instead of using a Tikhonov-type regularization for minimizing (19), one can apply, for example, a Landweber-Fridman-type iterative procedure 15. Invoking such an iterative procedure is deferred to future work.

6. Numerical simulations

In this section, we illustrate the method described in Section 5 by giving numerical results. Let the domain Ω be the interval (0, 1) and the final time T = 1. We choose the operator L as the negative Laplace operator, i.e. L = −Δ, the initial condition u(x, 0) = 2sin(πx) and homogeneous Dirichlet boundary conditions u(0, t) = u(1, t) = 0, where t ∈ (0, 1), in Equation (1). 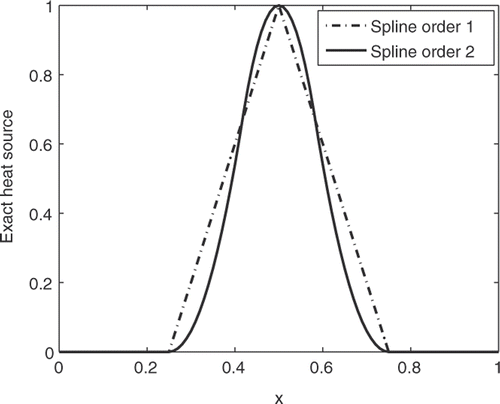The direct problem is described by (34) We consider the heat source given with the help of B-splines of order one and two, which reflects different smoothness of the solution u(·, ·) of the direct problem. We recall that the inverse problem we study here is to estimate the heat source f by the algorithm in section (19) given noisy measurements of u(·, 1). We illustrate in Figure 1 the exact heat source f as a spline of order one and two.

Figure 1. The exact heat source f as a spline of order one and two.

We use a piecewise linear ansatz as finite elements for the semi-discretization with respect to the spatial variable with M = 50 uniformly distributed nodes and the same uniform grid length is used for the time discretization. From classical results for the FEM, the order of convergence for our approximation space is 16. Since we aim to illustrate the stability of the problem, we consider noisy data with stochastic variance σ > 0, which corresponds to the deterministic noise level . Hence, we choose the mesh size M for the discretization of the problem to be smaller than , according to Section 4.1. For details of the FEM for the heat equation see Section 4.1, and further details can be found, for example, in 13,16.

To simulate our data, we assume an equally spaced deterministic design for our regression problem and we generate the data (Y_i)_i=1,…,N as where , i = 1, …, N, and ε_i are independent N(0, 1) random variables. To avoid an ‘inverse crime’ we choose 100 = N ≠ M.

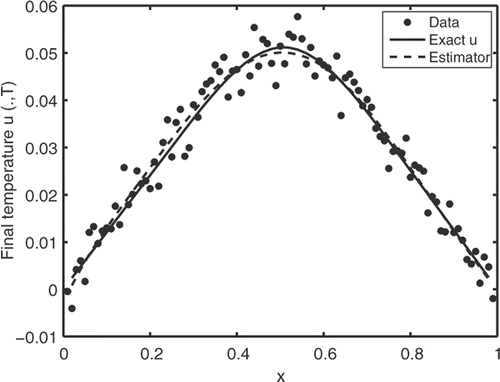
In the first step of our algorithm we estimate u(x, T) by a local polynomial estimator of order one, , with Gaussian kernel . Since our algorithm is data driven, we choose the bandwidth h by cross validation, which is a consistent adaptive choice of the smoothing parameter h (see, e.g. 17). In this case, we approximate the estimated squared error of ψ^(N) by a simple estimator In practical applications, we can also approximate the unknown variance σ by a consistent estimator (see, e.g. 18), making the method totally data-driven. Figure 2 shows the noisy data for a sample of size N = 100 and the local polynomial estimator of the exact data u(x, T) for the two cases we considered. Since is piecewise linear, it belongs to our ansatz space and it coincides with its Galerkin approximation.

Figure 2. The exact data, noisy data and the local polynomial estimator for σ = 0.1².

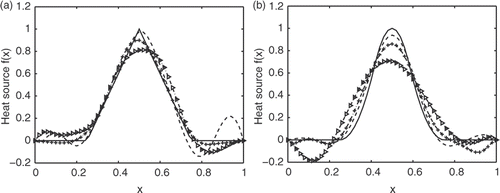
In the next step of our algorithm, we solve the minimization problem for the Tikhonov functional (30). We have at our disposal the Fréchet derivative of the operator J, but not the one of the operator A. Hence, we choose the steepest descent algorithm for the minimization of the Tikhonov functional. Even if this method is very slow, it converges to the global minimum of our functional. This minimum approximates well the exact solution f for a priori choice of the regularization parameter α ∼ β, as we noticed from the results in Section 5. Figure 3 illustrates the accuracy of the reconstruction of the spline of order one, respectively, two, for various amounts of noise. Since in this framework convergence results for statistical inverse problems in a continuous setting (when the variance σ → 0) are asymptotically equivalent to similar results in a discrete setting (as the sample size N → ∞), we consider the variance of the noise σ equal to 0.1², 0.05², 0.01² and we illustrate the results of Lemma 5.1, where the sequence of the regularization parameter is α ∼ β. We conclude that an accurate reconstruction of the heat source can be obtained with the proposed method given in Section 5 and, as expected, the accuracy increases when the variance decreases.

Figure 3. Estimation of the exact (–) heat source f for σ = 0.1² (− ⊳ −), 0.05² (− + −) and 0.01² (– – –). (a) Heat source f a spline of order one. (b) Heat source f a spline of order two.

7. Conclusion

We have proposed and investigated a stable numerical method for the problem of determining a spacewise-dependent heat source in the time-dependent heat equation, where only a finite amount of supplementary temperature measurements are given at a fixed time point, and these data are blurred by stochastic noise. The proposed method involves minimizing a certain functional using stochastic Tikhonov regularization, and in this method no a priori information is required on the noise level, i.e. the method is fully data driven. Numerical investigations were undertaken based on local polynomials, B-splines and cross-validation techniques. These numerical results show that accurate reconstructions of the heat source can be obtained without too many data points needed.