Determination of a time-dependent heat transfer coefficient in a nonlinear inverse heat conduction problem

Abstract

In this article, the determination of the time-dependent heat transfer coefficient, involving nonlinear boundary conditions of the third kind in the one-dimensional transient heat conduction from a non-standard boundary measurement is investigated. For this inverse, nonlinear, ill-posed problem, the existence and uniqueness of the solution are proved. Numerical results are obtained, using the boundary element method, and discussed.

Keywords:

• boundary element method
• heat conduction
• heat transfer coefficient
• inverse problem

1. Introduction

The (surface) heat transfer coefficient (HTC) characterizes the contribution that an interface makes to the overall thermal resistance to the system and is defined in terms of the heat flux across the surface for a unit temperature gradient. It is well-known that the HTC is an important value to determine in heat transfer, e.g. in the cooling of hot steel or glass in fluids or gases.

Non-intrusive experimental techniques to determine the HTCs currently in use, both in industry and academia, rely on certain theoretical models and temperature-driven physical phenomenon to accurately determine surface temperature histories. For instance, techniques based on characteristic colour changes of liquid crystal films at a given temperature 1 or on laser-induced fluorescence 2, both rely on the one-dimensional analytical temperature solution for a semi-infinite medium to determine the HTC at a point once the temperature history is obtained from the experiment. However, the impulsive change in boundary condition is difficult, if not impossible, to achieve in the laboratory. Moreover, traditionally transient experiments have been performed to evaluate HTC for steady-state processes, and thus this method is difficult to use in a truly time-dependent process where the HTC varies as a function of time.

Traditionally, partial boundary temperature and heat flux measurements are used as input to heat conduction models to extract the HTC values by solving a Cauchy ill-posed inverse heat conduction problem using, for example, Beck's function specification method, Tikhonov's regularization, Alifanov's iterative regularization or the mollification method 3–11. However, in this study we do not measure Cauchy data which may experience some practical difficulties, but instead we measure some non-standard boundary transient quantity of the heat conducting system, whilst allowing for convectional nonlinear boundary conditions of the third kind to be prescribed over the whole boundary. Further, the HTC is allowed to vary with time. Hence, a more realistic model can be proposed for the forced-convection flow boiling over the outer surface of a heated tube 8, quenching experiments 9, nucleate boiling on cylinders 7 or heat transfer in building enclosures 12.

As accurate values of the HTCs are critical for designing the thermal systems placed under increasingly harsh hostile conditions, a clear need to accurately model heat transfer in such cases exists in order to accurately reconstruct the HTC. Therefore, we consider an industrial device on whose boundary there is heat exchange with the ambient environment. This heat exchange is modelled as a linear or nonlinear boundary condition of the third kind. If it is linear, it describes the convective heat exchange with the environment taking place on the boundary of the space domain (Newton's law of cooling). If it is nonlinear, for the case of purely radiative transfer of energy, i.e. heat conduction subject to a black-body radiation at the surface, a fourth-order Stefan–Boltzmann power law is usual. The boundary condition of the third kind is the most important boundary condition for process simulation. It arises in the cooling of hot steel in fluids 13,14, or in the quenching heat treatment of metals in a liquid medium 15. It may also be considered as modelling the concentration of gaseous diffusion with a chemical reaction at the surface or, as the population density with a specific migration law at the boundary. The initial temperature of the body is given. Along with the temperature inside the solution domain, we seek to determine the time-dependent HTC from some additional information given by a non-standard boundary measurement. This inverse problem, where only boundary data is known, means that thermographic non-destructive testing can be performed in practice 16.

2. Mathematical formulation

Let us denote by Ω = (0, 1), Γ = ∂Ω and (u, v)_M = ∫_M uv for any Lebesgue measurable set M. In the case when M = Ω, we shall, for convenience, omit the subscript, i.e. (u, v) = ∫_Ω uv. The norm in L₂(Ω) is denoted by and analogously .

The following initial boundary value problem for the parabolic heat equation is investigated. Given t_f > 0 an arbitrary fixed time of interest, find the pair {T(x, t), σ(t)}, where T represents the temperature and σ is the time-dependent HTC satisfying (1) (2) (3) (4) where for some non-negative constants C and α. Examples of functions g satisfying (v) include the linear case g(T) = T, with C = α = 1, i.e. convective boundary conditions, and the nonlinear case g(T) = T³|T|, with C = 1, α = 4, i.e. radiative boundary conditions.

In order to solve (2.1–2.4) for the pair {T, σ} satisfying (i)–(v), we consider some additional information given by the non-standard boundary measurement (5) for some constants δ₀ and C₀, where E ∈ C²([0, t_f]) is a given function and (6) denotes the primitive (anti-derivative) of g. Although the quantity E does not have a very clear physical meaning, we mention that Equation (2.5) can be viewed as a non-local, non-standard boundary condition. Such non-standard formulations of inverse heat conduction problems have been considered before elsewhere (see, e.g. 17–19). Finally, note that the linear case g(T) = T has already been investigated recently by the authors 20, and in this article the analysis is extended to the nonlinear case satisfying condition (v).

3. The direct problem

3.1. Variational formulation

The variational formulation of the direct problem (2.1–2.4) for a given σ satisfying (i) reads as follows.

Definition 3.1

A function T_σ ∈ L₂((0, t_f), H¹(Ω)) with ∂_tT_σ ∈ L₂((0, t_f), L₂(Ω)) is called a weak solution to the direct problem (2.1–2.4) if T_σ(x, 0) = T⁰(x) and (7)

One can show that there is a unique weak solution to the direct problem (2.1–2.4) (see, e.g. 21).

We will need the following compatibility condition later. We assume that there exist σ₀ ≥ 0 and such that (8) The condition (3.2) implies the compatibility of the boundary condition and the initial condition at time t = 0.

Finally, as is usual in papers of this sort, C, ϵ and C_ϵ will denote generic positive constants depending only on a priori known quantities, where ϵ is sufficiently small and C_ϵ is large.

3.2. Regularity

The energy estimates for T_σ can be obtained in the standard way. Setting ϕ = T_σ in (3.1) and integrating the result in time we readily obtain Gronwall's lemma implies that (9) Choosing ϕ = ∂_tT_σ in (3.1) and integrating the result in time we readily obtain Now, we can write using (i) and (2.6) Further, on applying (iv) we have Putting things together and applying Gronwall's lemma, we deduce that (10) Let us note that the relations (3.3) and (3.4) describe the natural regularity of a weak solution to (3.1) and they also use the conditions on the data. Uniqueness is a simple consequence of the monotonic behaviour of g and the Gronwall lemma. Higher regularity of T_σ can be obtained in a similar way by adopting additional conditions on the data, namely (11) Then, differentiating (3.1) with respect to the time variable, setting ϕ = ∂_tT_σ and integrating the result in time we obtain Integration by parts implies that By standard arguments, we obtain the following regularity of T_σ using Gronwall's lemma: (12)

4. Solvability

In this section, we prove the existence and uniqueness, i.e. the solvability, of a (weak) solution {T_σ, σ} to the inverse problem (2.1–2.5). We will use Rothe's method 22 for the time discretization. We split the whole time interval [0, t_f] into n equidistant subintervals [t_i−1, t_i] with the length and t_i = iτ for . We introduce the following notation for the backward difference for , for any function u. Thus, we are left with the following recursive system of steady-state inverse problems.

For 1 ≤ i ≤ n, find a couple {T_σi, σ_i} such that E(t_i) = ∫_ΓΦ(T_σi) and (13) along with T_σ0 = T⁰.

According to the results from 23, we see that (4.1) admits a unique solution {T_σi, σ_i} if (14) where T₀(t_i) is the unique solution of the direct problem (4.1) with σ_i = 0.

Next, in Lemmas 4.1–4.3, we perform some stability analysis.

4.1. Stability analysis

LEMMA 4.1

There exists a C > 0 such that

Proof

Take any 1 ≤ j ≤ n. Put ϕ = T_σiτ into (4.1) and sum all the results for 1 ≤ i ≤ j. We obtain (15) The following inequality 24 plays an important role in the estimation process: (16) We use the Cauchy and Young inequalities, together with (4.4), to estimate the right-hand side of (4.3) as follows: This, together with (4.3), gives for a sufficiently small fixed ϵ > 0, that An application of Gronwall's lemma yields which is valid for any 1 ≤ j ≤ n. This implies the desired result.▪

LEMMA 4.2

Assume that (2.5) holds. Then there exist C, τ₀ > 0 such that

Proof

Take any 1 ≤ j ≤ n. Put ϕ = δT_σiτ into (4.1) and sum up the result for 1 ≤ i ≤ j. We obtain (17) According to the behaviour of g in (v) we can write (18) Therefore, using (2.5) we deduce that An application of the Cauchy and Young inequalities implies that We apply the Abel summation, Cauchy and Young inequalities and (4.4) to obtain Summarizing all the estimates we have obtained and choosing a sufficiently small ϵ > 0, we arrive at which is valid for any 1 ≤ j ≤ n. This implies the desired result.▪

LEMMA 4.3

Assume that (2.5) and (3.2) hold. Then there exist C, τ₀ > 0 such that

Proof

Take any 1 ≤ j ≤ n. Subtract (4.1), for i = i − 1, from (4.1). For the case when i = 1, use the compatibility condition (3.2) with δT_σ0 = ∂_tT_σ(0). Then put ϕ = δT_σi and sum all the results for 1 ≤ i ≤ j. We have (19) Using the Cauchy and Young inequalities and the trace theorem, we deduce that (20) and (21) The Abel summation gives (22) Using (4.6) we can write (23) where δE_i = (E(t_i) − E(t_i−1))/τ. Thus (24) The relations (4.10–4.12) give (25) Here, in addition of (iii), we also require . However, if σ₀ = 0, we only require ∂_tT_σ0 ∈ L₂(Ω). We recall from (2.5) that we have E′ ≥ δ₀ > 0. Therefore for τ ≤ τ₀ we deduce that δE_j is strictly positive and it cannot approach zero. Putting things together and choosing a sufficiently small ϵ > 0, we arrive at which is valid for any 1 ≤ j ≤ n. From this we can easily conclude the proof.▪

Now, let us introduce the following piecewise linear in time function and the step functions In the same way we define the step functions and . Using this notation, we rewrite (4.1) in the following form: (26)

Now, we are in a position to prove the existence of a weak solution to our inverse problem.

4.2. Existence and uniqueness

THEOREM 4.1

Assume that (2.5) and (3.2) hold. Then there exists a solution {T(x, t), σ(t)} to (2.1–2.5) satisfying (i)–(v) if (27) where T₀ is the unique weak solution of the direct problem (2.1–2.4) with σ = 0.

Proof

By virtue of the a priori estimates from Lemmas 4.1–4.3, and using Lemma 1.3.13 from 22, we observe that there exists a subsequence of T_σn (which we denote by the same symbol again to avoid unnecessary subscripts) such that (28) Using (4.4), we observe that Thus which is valid for all small ϵ > 0. Therefore In 1-D this implies the pointwise convergence. In higher dimensions we obtain the pointwise convergence a.e. on the boundary. From the continuity of g, we observe that The fact that is uniformly bounded allows us to write Now, take any t ∈ [0, t_f]. We integrate (4.14) in time over (0, t) and we obtain (29) According to the above considerations, we pass to the limit for τ → 0 and observe that (30) Finally, we differentiate this identity with respect to the time variable to conclude the proof of the existence of a weak solution.

The relation (4.15) follows from (4.2) when passing to the limit τ → 0.▪

The next theorem addresses the uniqueness of the solution of our inverse problem.

THEOREM 4.2

Let T_σ, be two weak solutions of the problem (2.1–2.4) according to Definition 3.1 corresponding to σ and , respectively. If T_σ, satisfy (ii) and , i.e. if , then and .

Proof

Subtract the variational formulations (3.1) for both solutions {T_σ, σ} and from each other and set . We obtain (31) It holds (32) Using (4.6) we deduce that Therefore, when we integrate (4.19) in time, we easily observe that which implies that in [0, t_f].

Subtracting the variational formulations (3.1) for both solutions {T_σ, σ} and from each other and using that , we obtain Using , we obtain (33) The relation (4.6) implies that According to the fact that E(t) > 0, we obtain from the relation (4.21) for ϕ = T_σ that , and this concludes the proof.▪

5. Boundary element method

Applying Green's formula, the heat equation (2.1) transforms into (see, e.g. 25) (34) where the initial condition (2.2) has also been imposed, (35) is the fundamental solution for the one-dimensional heat equation, H is the Heaviside function which is introduced in order to emphasize the fact that the fundamental solution is zero for t ≤ τ, and in (5.1), η(0) = η(1) = 1/2 and η(x) = 1 for x ∈ (0, 1).

Introducing the boundary conditions (2.3) and (2.4) into (5.1) results in (36) Applying the integral equation (5.3) at the boundary (x, t) ∈ {0, 1} × (0, t_f], one obtains two nonlinear integral equations in the three unknowns T(0, t), T(1, t) and σ(t). A further nonlinear equation is given by the measurement (2.5) which, when contaminated with multiplicative noise, reads as (37) where ρ is the percentage of noise and ε is a random variable taken from a uniform distribution in the interval [−1, 1] using the numerical algorithms (NAG) routine G05DAF.

Using a boundary element method (BEM) with constant elements (N₀ uniform cells for discretizing the space domain (0, 1) and N uniform constant boundary elements for discretizing the time interval [0, t_f]), we obtain a nonlinear system of 3N equations with 3N unknowns, which is solved using the NAG routine E04FCF in a nonlinear least-squares minimization sense. The constraint (i) that σ is non-negative is not imposed in order to avoid a more sophisticated constrained minimization problem. However, if it happens that σ takes negative values (Figures 2e and 3c), then these values are to be interpreted as zero values.

6. Numerical results and discussion

In order to illustrate and discuss the numerical results obtained by the BEM, we take t_f = 1, and the input data T⁰(x) = x², h₀(t) = 16t⁴(t + 1), h₁(t) = (1 + t)(1 + 2t)⁴ + 2, g(T) = T³|T|, f(x, t) = 0 and E(t) = 12.8t⁵ + 16t⁴ + 16t³ + 8t² + 2t + 0.2. Then, according to Theorems 4.1 and 4.2, the inverse problem (2.1–2.5) has a unique solution. 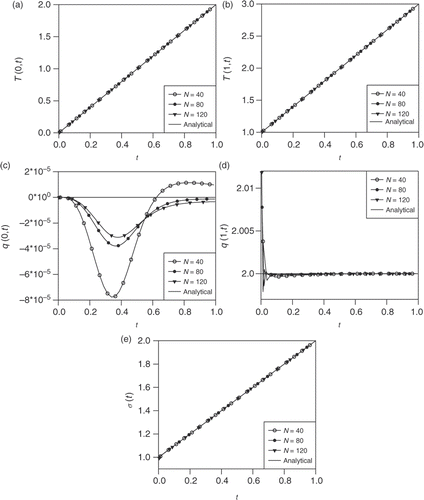It can be verified through direct substitution that this solution is given by (38) The numerical results for the boundary temperatures T(0, t) and T(1, t), the heat fluxes q(0, t) and q(1, t) and the HTC σ(t), obtained when in the BEM, N₀ = 40 and N is increased gradually from 40 to 120, and there is no noise, i.e. ρ = 0 in (5.4), are shown in Figures 1(a)–(e), respectively. From these figures it can be seen that the numerical solution converges to the exact solution, as the number of boundary discretizations N increases. Further, the results obtained are sufficiently accurate when (N, N₀) = (40, 40), and therefore, in the next figures we present numerical results obtained with this mesh size only.

Figure 1. The analytical and numerical boundary temperatures (a) T(0, t) and (b) T(1, t), the heat fluxes (c) q(0, t) and (d) q(1, t), and the HTC (e) σ(t), as functions of time t, when N increases from 40 to 120, N₀ = 40 and no noise, i.e. ρ = 0, is introduced in the measurement (5.4).

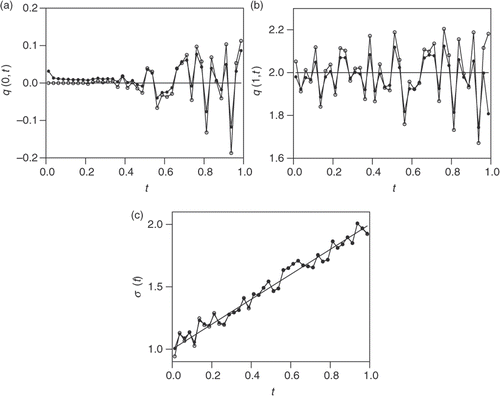
When noise is gradually introduced into the additional condition (5.4) from ρ = 0 to ρ = 5% and then to ρ = 10% (Figure 2f), we observe that the computed boundary temperatures T(0, t) and T(1, t) (Figures 2a and b), respectively, appear to remain stable when increasing the amount of noise, i.e. the numerical boundary temperature deviates from the analytical solution proportional to the amount of noise. This indicates that the results for the boundary temperature do not require regularization for the test example under investigation. In contrast to this, the numerical results for the heat fluxes q(0, t) and q(1, t) (Figures 2c and d), respectively, and the HTC σ(t) (Figure 2e), obtained when the amount of noise is increased become unstable. This is to be expected since higher-order derivatives are more difficult to calculate accurately than lower-order derivatives. In order to stabilize the results obtained for the heat fluxes, the regularization is necessary 26,27. This is achieved by solving the direct problem for the heat equation (2.1) subject to the initial condition (2.2) and the noisy Dirichlet temperature boundary conditions taken from Figures 2(a) and (b), using the Tikhonov regularization method with the choice of the regularization parameter based on the L-curve method. Then the regularized heat fluxes q(0, t) and q(1, t) (Figures 3a and b), respectively, and the HTC σ(t) (Figure 3c) undergo some improvement in stability.

Figure 2. The analytical and numerical boundary temperatures (a) T(0, t) and (b) T(1, t), the heat fluxes (c) q(0, t) and (d) q(1, t), the HTC (e) σ(t), and the measurement (f) E(t), as functions of time t, when the amount of noise in (5.4) is ρ ∈ {0, 5%, 10%}.

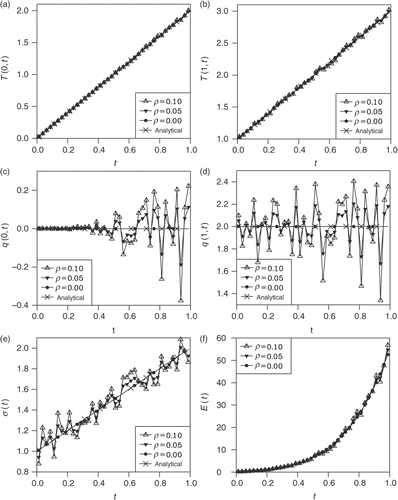
Figure 3. The (—) analytical and numerical heat fluxes (a) q(0, t) and (b) q(1, t), and the HTC (c) σ(t), as functions of time t, when the amount of noise in (5.4) is ρ = 5%, (–○–) unregularized solutions from Figures 2(c)–(e), and (–•–) regularized solutions with the regularization parameter λ = 1.2 × 10⁻³.

7. Conclusions

In this article, we have investigated an inverse heat conduction problem with unknown nonlinear boundary conditions. We have proved the solvability of the inverse problem. We have used the BEM to construct and solve numerically the missing terms involving the boundary temperatures, heat fluxes and the HTC. In the numerical example, when the number of discretizations increases, for exact data, the numerically obtained results are accurate and convergent. However, when noise is introduced in the non-standard boundary measurements, we obtained stable solutions for the boundary temperatures, whereas the numerical solutions for the heat fluxes and the HTC deviate much from the analytical solution, indicating that some instability may occur. To further stabilize the solution, we have used the Tikhonov regularization method, which resulted in some improvement in the approximations. Future work will involve extending the numerical BEM introduced in this study to higher-dimensional inverse HTC identification problems.

Acknowledgements

Slodička was supported by the BOF/GOA-project No. 01G00607 of Ghent University and the grant number 3G008206 of the Fund for Scientific Research–Flanders.