Determining a stable relationship between hedge fund index HFRI-Equity and S&P 500 behaviour, using filtering and maximum likelihood

Abstract

In this article we test the ability of the stochastic differential model proposed by Fatone et al. [Maximum likelihood estimation of the parameters of a system of stochastic differential equations that models the returns of the index of some classes of hedge funds, J. Inv. Ill-Posed Probl. 15 (2007), pp. 329–362] of forecasting the returns of a long-short equity hedge fund index and of a market index, that is, of the Hedge Fund Research performance Index (HFRI)-Equity index and of the S&P 500 (Standard & Poor 500 New York Stock Exchange) index, respectively. The model is based on the assumptions that the value of the variation of the log-return of the hedge fund index (HFRI-Equity) is proportional up to an additive stochastic error to the value of the variation of the log-return of a market index (S&P 500) and that the log-return of the market index can be satisfactorily modelled using the Heston stochastic volatility model. The model consists of a system of three stochastic differential equations, two of them are the Heston stochastic volatility model and the third one is the equation that models the behaviour of the hedge fund index and its relation with the market index. The model is calibrated on observed data using a method based on filtering and maximum likelihood proposed by Mariani et al. [Maximum likelihood estimation of the Heston stochastic volatility model using asset and option prices: An application of nonlinear filtering theory, Opt. Lett., 2 (2008), pp. 177–222] and further developed in Fatone et al. [Maximum likelihood estimation of the parameters of a system of stochastic differential equations that models the returns of the index of some classes of hedge funds, J. Inv. Ill-Posed Probl. 15 (2007), pp. 329–362; The calibration of the Heston stochastic volatility model using filtering and maximum likelihood methodsin Proceedings of Dynamic Systems and Applications, Vol. 5, G.S. Ladde, N.G. Medhin, C. Peng, and M. Sambandham, eds., Dynamic Publishers, Atlanta, USA, 2008, pp. 170–181]. That is, an inverse problem for the stochastic dynamical system representing the model is solved using the calibration procedure. The data analysed is from January 1990 to June 2007, and are monthly data. For each observation time, they consist of the value at the observation time of the log-returns of the HFRI-Equity and of the S&P 500 indices. The calibration procedure uses appropriate subsets of data, that is the data observed in a 6 months time period. The 6 months data time period used in the calibration is rolled through the time series generating a sequence of calibration problems. The values of the HFRI-Equity and S&P 500 indices forecasted using the calibrated models are compared to the values of the indices observed. The result of the comparison is very satisfactory. The website http://www.econ.univpm.it/recchioni/finance/w8 contains some auxiliary material including some animations that helps the understanding of this article. A more general reference to the work of some of the authors and of their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.

Keywords:

• stochastic volatility model
• filtering theory
• calibration problem

1. Introduction

In this article we test on real data the model proposed in 1 that describes the dynamics of a market index and of the index of some classes of hedge funds. Let us recall the model. We denote with t the time variable, and with (x_t, z_t, v_t), t > 0, a stochastic process. We interpret x_t, t > 0, as the log-return of a market index, z_t, t > 0, as the log-return of the index of a class of hedge funds and v_t, t > 0, as the stochastic variance of the market index. For t > 0 x_t, z_t and v_t are real random variables. In this article we consider the S&P 500 index as market index and the HFRI-Equity hedge fund index as index of a class of hedge funds. The model proposed in 1 can be used with several other choices of the meaning for the indices. In 1 the dynamics of the stochastic process (x_t, z_t, v_t), t > 0, is modelled with the following system of stochastic differential equations with initial conditions: (1) (2) (3) where , , , t ≥ 0, are standard Wiener processes such that and , , t > 0, are their stochastic differentials. The quantities χ, ϵ, θ, β and γ are real constants known as model parameters. We choose χ, ϵ, θ to be positive constants such that . This last assumption guarantees that when is positive with probability one, v_t, solution of (3) remains positive with probability one for t > 0. Note that , , are random variables that we assume to be concentrated on a point with probability one. For simplicity, we identify these random variables with the points where they are concentrated. In real markets, the random variables and are observable and the random variable cannot be observed. We note that, as shown later, without loss of generality we can choose , . We choose to be a positive constant that must be determined in the calibration of the model. Moreover we assume that (4) where ⟨·⟩ denotes the expected value of ·, and the quantities ρ_1,2, ρ_1,3, ρ_2,3 ∈ [−1, 1] are constants known as correlation coefficients. We remind that the autocorrelation coefficients of , i = 1, 2, 3, are equal to one.

Equations (1) and (3) are the well-known Heston stochastic volatility model 2. This model was introduced with the aim of overcoming some limitations of the Black–Scholes model 3 that are pointed out by market data such as, for example, the assumption of constant volatility. Letting S_t, t > 0, be the price at time t of an asset, the Heston model (1) and (3) describes the dynamics of the log-return x_t = log(S_t/S₀), t > 0, of the asset and of its stochastic variance v_t, t > 0. Note that with the previous choice, when t = 0 we have and in a similar way we have . A systematic data analysis has shown that the Heston stochastic volatility model is well-suited to model the behaviour of several market indices such as, for example, the S&P 500 index, the Down-Jones Industrials index and the Nasdaq Composite index (see 4,5). We note that Equation (3) is known as the equation that defines the mean-reverting process with speed χ and parameters θ and ϵ.

The model introduced in 1 and considered here is obtained adding to the Heston stochastic volatility model (1) and (3) a third equation, that is Equation (2), that describes the behaviour of the log-return of the index of some classes of hedge funds. In fact statistical studies, such as 6–9, of the time series of the data relative to the log-returns of the indices of several classes of hedge funds have shown that the log-returns of the indices of some classes of hedge funds are related to the log-returns of the S&P 500 index. In particular in 9 some discrete time models are proposed to study nine different classes of hedge funds. The model proposed in 9 to describe the dynamics of the index of the ‘long-short equity’ class of hedge funds is based on the assumption that up to a stochastic additive error there exists a kind of direct proportionality between the behaviour of the variation of the log-return of the index of the ‘long-short equity’ class of hedge funds and the variation of the log-return of the S&P 500 index. In 9, this assumption is supported by convincing empirical evidence. We can conclude that interpreting z_t, t > 0, as the log-return at time t of an index of the ‘long-short equity’ class of hedge funds, that is the HFRI-Equity index, x_t, t > 0, as the log-return at time t of the S&P 500 index and v_t, t > 0, as the stochastic variance of x_t, t > 0, the system of stochastic differential Equations (1–3) can be seen as a reasonable translation in continuous time of the model proposed in 9. In fact Equation (2) states that dz_t is given by the sum of β dx_t and a random disturbance given by .

The calibration problem of model (1–3) can be stated as follows: given a discrete set of time values t = t_i, i = 0, 1, …, n, such that t₀ = 0, t_i < t_i+1, i = 0, 1, …, n − 1, and the observation , of the log-returns of the market and of the hedge fund indices, that is the observation of (x_t, z_t), at time t = t_i, i = 0, 1, …, n, determine the values of the parameters appearing in (1), (2) and (3), of the correlation coefficients ρ_1,2, ρ_1,3, ρ_2,3 and of the initial stochastic variance . For later convenience we define t_n+1 = +∞. The choice t₀ = 0 corresponds to choosing the origin of the time axis in the first observation time where we choose . The choice of the origin of the time axis can be changed without changing substantially the problem considered. Note that the calibration problem is an inverse problem for the model (1), (2) and (3). In fact the calibration problem consists of the reconstruction of the parameters of the model, of the correlation coefficients of the Wiener processes and of the initial stochastic variance from the observation at discrete times of the variables x_t, z_t, t > 0.

In order to study time series of real data, the calibration problem of model (1–3) stated previously has been solved using the approach suggested in 1 based on the methods of filtering and maximum likelihood. This approach was introduced in the context of mathematical finance in 10 and further developed in 1,11.

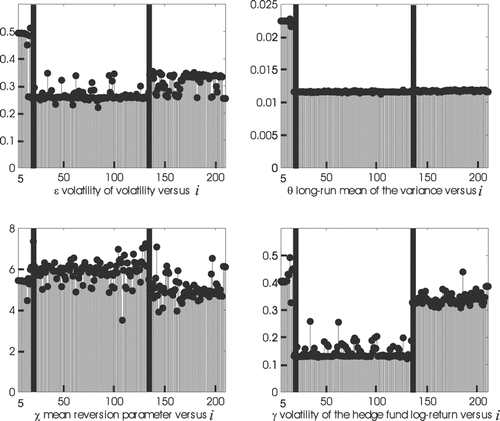
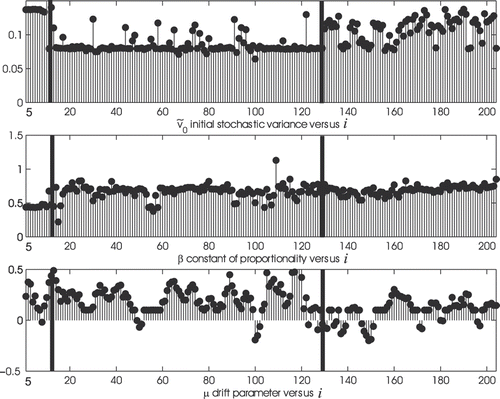
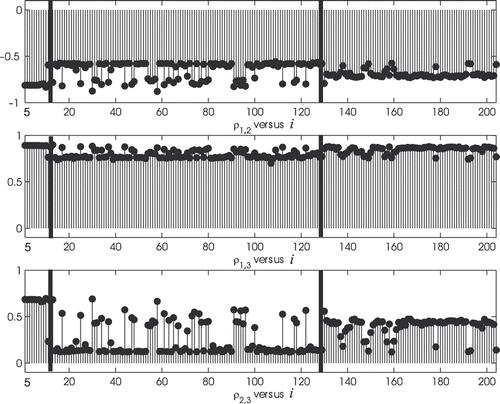
We consider the time series of monthly data of the S&P 500 and of the HFRI-Equity indices covering a period of 210 months from 31 January, 1990 to 30 June, 2007. The observation times will be denoted by , i = 1, 2, …, 210, and, for later convenience, we introduce corresponding to 31 December, 1989 and the observations of the values of the indices at time . From these data we derive the time series of the log-returns. We have applied the calibration procedure mentioned above using as data the data contained in a window of six consecutive observation times (that is a window covering the data relative to a period of 6 months). This choice is motivated in Section 3. The numerical results obtained considering the 206 (6 months) data windows obtained from the data time series are presented in Section 3 and show that the solutions of the calibration problems considered are really associated with the data time series, that is they are ‘stable’ when the time window of the data used in the calibration is shifted. In fact, as shown in Figures 1–3, the vector as Θ* solution of the calibration problem, as a function of the time window of the data used in the calibration, can be grouped into three sets associated with the data of three non-overlapping time periods and in these three sets the vectors Θ* found are approximately constants (see Section 3 for further details). After having calibrated the model using the data belonging to a 6 month window we use the resulting estimate of Θ to make the forecasts of the market and of the hedge fund indices 1, 3 and 6 months in the future counting as future the time after the last observation time contained in the data window used in the calibration. The forecasted values of the market and of the hedge fund indices are obtained using some formulae derived in 1 that adapt to the model (1–3) standard formulae of filtering theory. For the convenience of the reader these formulae are recalled in Section 2.

Figure 1. Reconstruction of the parameters ε, θ, χ, γ (in ordinate) of the model (1–3), as a function of the index i (in abscissa) of the last observation time contained in the data window used in the calibration.

The quality of these forecasts is established a priori (i.e.‘model implied’) using filtering theory and a posteriori (i.e. ‘empirically’) comparing the forecasted values with the historical data. The results obtained suggest that the model proposed describes satisfactorily the data, and that high quality forecasts (several months in the future) of the value of the hedge fund index returns can be obtained using the model. Forecasts of approximately the same quality are obtained for the returns of the market index. We remark that the forecasts that are expected to be good a priori (‘model implied’) on the basis of filtering theory are a posteriori (‘empirically’) better than the average forecast, that is, compared to historical data, these forecasts are better than the average forecast. This last fact can be really relevant in practical situations.

Figure 2. Reconstruction of the initial stochastic variance and of the parameters β, (in ordinate) of the model (1–3), as a function of the index i (in abscissa) of the last observation time contained in the data window used in the calibration.

From a macro point of view the three different time periods selected by the data analysis do not correspond exactly to different business cycles but they represent relevant economic periods that could be interesting to describe briefly.

Figure 3. Reconstruction of the correlation coefficients ρ_1,2, ρ_1,3, ρ_2,3 (in ordinate) of the model (1–3), as a function of the index i (in abscissa) of the last observation time contained in the data window used in the calibration.

Period 1 started with the end of the US expansion, which began after the 1987 collapse and it finished in the bulk of the 1990–1991 US recession started in July 1990. So Period 1 includes the end of an economic expansion and the starting point of a recession.

Period 2 is the longest US economy expansion ever seen in the US history. So, a long positive performing cycle that had its peak in March 2001 (Period 3) and that caused one of the major bubbles in US history (Period 3).

Period 3 includes two different environments: the burst of the so called ‘US IT bubble’ (with the end of the 1990s economic growth) and the recovery period still in place in 2008 (and started technically in March 2003).

The traditional approach followed by practitioners to forecast z_t, t > 0, is the use of discrete time models and linear regression analysis, with which (referred to our notation) one determines only z_t as a function of x_t and one does not consider v_t; a more sophisticated method is to use multi-regressions (linear or quadratic), but always in order to describe (HFRI returns) in respect to different explicative variables (generally market indices). One supposes that volatility does not follow a stochastic process and that the past history of a fund, or of an index, can be repeated in the future, with a confidence level. Volatility at time t depends on N previous data, that is (5) where is the estimated value of the volatility at time t, Δt is the discrete time step, x_t−iΔt, i = 1, 2, …, N, are observed log-returns and is the average of the observed log-returns. This strongly restrictive assumption leads to calculate values of β in the linear regression that depends too much from the data period considered: in our case, the total β calculated in the entire observation period (from 31 January, 1990 to 30 June, 2007) will be completely different with respect to the three values of β (different among themselves) calculated in the three periods (that is: Period 1: from 31 January, 1990 to 31 October, 1990; Period 2: from 30 November, 1990 to 31 October, 2000; Period 3: from 30 November, 2000 to 30 June, 2007).

Several approaches have been used to overcome this difficulty such as, for example, those proposed by Bollerslev 12 and Pearson 13. As shown in 6, this last approach is quite useful in the case of hedge indices when used to study data since the year 2000, however, it is less satisfactory when applied to single funds.

This article is organised as follows: in Section 2 we present the calibration procedure and the formulae used to make the forecasts of the log-returns of the indices and of the stochastic variance. Numerical results are presented in Section 3. In particular, the analysis of the forecasted log-returns is carried out and their quality is established. In Section 4 we draw some conclusions. Finally, in the Appendix we give some formulae useful for the implementation in a computer code of the numerical methods summarized in Section 2.

2. The calibration procedure and the formulae used to forecast the log-returns

Let us summarize the procedure used to solve the calibration problem formulated in the Introduction and let us recall some formulae used to forecast the log-returns x_t, z_t, t > 0, the stochastic variance v_t, t > 0, and to evaluate the quality of the forecasts. A more detailed explanation of these formulae is contained in 1.

Let ∈ ℝ¹⁰ be the vector of the model parameters, of the correlation coefficients and of the initial stochastic variance and let ℳ = Θ = |χ > 0, ϵ > 0, θ > 0, β ≥ 0, γ ≥ 0, be the set of feasible vectors. It is easy to see that the conditions that define ℳ express some elementary properties of the Heston stochastic volatility model and of the correlation coefficients. In detail, we denote with t > 0, the set of observations of the variables x_t and z_t available at time t > 0 and, given Θ, we denote with (x, z, v) ∈ ℝ × ℝ × ℝ⁺, t > 0, the joint probability density function of having x_t = x, z_t = z and v_t = v at time t > 0 conditioned to the observations contained in ℱ_t, t > 0, and to the initial condition . We remark that the initial conditions and are already contained in ℱ_t, t > 0. Note that we assume that the observations are known exactly, that is, they are known without the uncertainty that usually is represented in the observation process as an additive random variable. The (inverse) calibration problem considered here is translated into the following optimization problem: (6) where the log-likelihood function F(Θ) is given by (7) that is, the function F(Θ) is the sum of logarithms of integrals in dv′ of the probability density functions , i = 0, 1, …, n − 1, of making the observations actually made, that is, for i = 0, 1, …, n − 1, the probability of observing at time t = t_i+1 given the fact that the observations ℱ_ti have already been made at time t = t_i. Note that for i = 0, 1, …, n, when t_i < t < t_i+1 we have ℱ_t = ℱ_ti. In (7), denotes the left limit of as t → t_i.

The optimization problem (6) is a maximum likelihood problem and its solution Θ* is the solution of the calibration problem, that is, the components of Θ* are the estimates of the model parameters, of the correlation coefficients and of the initial stochastic variance obtained from the data.

We note that the choice (7) of the log-likelihood function as objective function of problem (6) is only one possible choice between many other possibilities.

Let us consider the joint probability density function (x, z, v) ∈ ℝ × ℝ × ℝ⁺, t > 0, of having x_t = x, z_t = z, v_t = v given ℱ_t, t > 0, and Θ. Recall that . The joint probability density function is the solution of a filtering problem, and in 1 it has been shown that is given by (8) where p_f (x, z, v, t, x′, z′, v′, t′|Θ), (x, z, v), (x′, z′, v′) ∈ ℝ × ℝ × ℝ⁺, t, t′ > 0, t − t′ > 0, is the fundamental solution of the Fokker–Planck equation associated with the system of stochastic differential Equations (1–3) and (9) where δ is Dirac's delta. Similar filtering problems for the Heston model have been studied in 10,11.

In order to determine the vector Θ we solve the calibration problem, that is, we solve the optimization problem (6). We use a computationally efficient procedure presented in 1 and summarized in the Appendix to evaluate the functions , v ∈ ℝ⁺, i = 1, 2, …, n, on a grid in the v variable. We maximize the (log-)likelihood function (7) using as optimization method a variable metric steepest ascent method introduced in 1 obtained adapting to the present circumstances the method developed in 14 to solve the linear programming problem. This method is a kind of steepest ascent method based on an iterative procedure that searches the maximum likelihood estimate Θ*, solution of (6), beginning from an initial guess Θ⁰ ∈ ℳ and that for k = 1, 2, … generates at step k a vector Θ^k ∈ ℳ satisfying the inequality F(Θ^k) ≥ F(Θ^k−1). That is, the objective function is monotonically non-decreasing along the sequence {Θ^k}, k = 0, 1, …. In the numerical experiment, presented in Section 3, in this optimization procedure we use the following condition as stopping rule: (10) where δ₁ and k_max are positive constants that will be chosen later.

Given the joint probability density function (x, z, v) ∈ ℝ × ℝ × ℝ⁺, t ≥ 0, (in particular, given Θ obtained solving the optimization problem (6)) we can forecast the values of the market index log-return, of the hedge fund index log-return x_t, z_t, t > 0, t ≠ t_i, i = 0, 1, …, n, and of the stochastic variance v_t, t > 0, using, respectively, the mean values t > 0, conditioned to the observations contained in ℱ_t, t > 0, of the random variables x_t, z_t, v_t, t > 0, that is, (11) (12) (13) The notation 𝔼(· | +) means expected value of · conditioned to +. As shown in 1 from formulae (8), (11–13) and (36) of the Appendix, we can deduce that (14) (15) (16) Recall that we use the notation t_n+1 = +∞. Note that from (14) and (15) it follows that and i = 0, 1, …, n.

The main advantage of formulae (14–16) when compared to formulae (11–13) consists of the fact that (14–16) contain only a one-dimensional integral that can be evaluated numerically very efficiently once the integrand function is known on a suitable one-dimensional grid, whilst (11–13) contain a three-dimensional integral whose numerical evaluation requires the knowledge of the integrand function on a three-dimensional grid.

The ‘model implied’ quality of the estimates (11–13) (or equivalently of the estimates (14–16)) depends on the variance of the random variables x_t, z_t, v_t, t > 0, conditioned to the observations contained in ℱ_t, t > 0, that is, we can estimate the (‘model implied’) quality of the estimates (11–13) computing, respectively, the quantities (17) (18) (19) As shown in 1, denoting with ξ_t, t > 0, the state variable x_t, t > 0, or the state variable z_t, t > 0, and with and the observation or the observation of , i = 0, 1, …, n, and the mean value conditioned to the observation contained in ℱ_t, t > 0, of ξ_t, t > 0, respectively, an elementary computation gives the following formula for the conditioned variance of the state variables x_t and z_t, t > 0: (20) where the constants l₁, l₂, l₃ and l₄ are defined as follows: (21) (22) (23) (24) and finally, for the conditioned variance v_t, t > 0, we have (25) Note that Σ²(·|ℱ_t, Θ) = 𝔼((· −𝔼(·|ℱ_t, Θ))²|ℱ_t, Θ), t > 0, and that the estimates (11–13) are supposed to be of high quality when the variances (17–19) are small. In the data analysis described in Section 3 we use formulae (11–13) to forecast the values of x_t, z_t, t > 0, t ≠ t_i, i = 0, 1, …, n, and of the stochastic variance v_t, t > 0, coherently with the observations contained in ℱ_t, t ≥ 0. The quality of the forecasts of the values of x_t, z_t, t > 0 is evaluated ‘model implied’ using formula (20) and established ‘empirically’ comparing the forecasts with the historical data. We recall that the stochastic variance v_t, t > 0, cannot be observed.

3. Analysis of the S&P 500 and HRFI-Equity data

Let us present the results obtained applying the procedure described in Section 2 to the historical time series of 210 monthly data relative to the variation ΔI_x,i of the S&P 500 index I_x,i, and the variation ΔI_z,i of the HFRI-Equity index I_z,i, i = 1, 2, …, 210. The variations ΔI_x,i, ΔI_z,i of I_x,i−1, I_z,i−1, respectively, are measured in per cent i = 1, 2, …, 210. The data cover the period of 210 months from 31 January, 1990 to 30 June, 2007. The observation dates , i = 1, 2, …, 210, are the last day of the month (i.e. 31 January, 28 February, 31 March, 30 April, 31 May, 30 June, 31 July, 31 August, 30 September, 31 October, 30 November, 31 December). First of all, we have processed the data ΔI_x,i, ΔI_z,i, in order to get the time series of the observed log-return , of the S&P 500 index and of the observed log-return , i = 1, 2, …, 210, of the HFRI-Equity index. We have added to these data the observation at date corresponding to 31 December, 1989. We choose I_x,0 = I_z,0 = 1 and . We have used the following recursive formulae to construct the log-returns: (26) (27) Recall that , correspond to the log-returns at time (31 December, 1989). The indices I_x,0, I_z,0 are chosen equal to one and I_x,i, I_z,i, are related to the monthly log-returns , , i = 1, 2, …, 210, given in (26) and (27) by the following formulae: (28) (29) that is, we have (30) (31) In the following, we refer to I_x,i, I_z,i, i = 0, 1, …, 210, and to x_t, z_t, t > 0, as the S&P 500 index, the HFRI-Equity index and their log-returns, respectively, as a function of time. The quantities I_x,i, I_z,i, i = 0, 1, …, 210, are not the actual values of the indices since they are obtained starting the data time series from the values I_x,0 = 1, I_z,0 = 1. We can conclude that the values of the indices have been rescaled dividing them by suitable normalization constants.

We consider a window of six observation times (that is a window covering a time period of 6 months) corresponding to 12 data and we move from a window to the next one removing the data relative to the first observation time of the window and adding the data corresponding to the observation time that follows the last observation time of the window. That is the j-th window contains the data , i = 1, 2, …, 6, j = 1, 2, …, 206. For each data window we solve the calibration problem (6). That is, we solve 206 calibration problems. Recall that in the solution of each calibration problem, coherently with the statement of the problem given in the Introduction, we translate the zero of the time axis to the first observation time of the data window considered and we adapt the data to this translation of the time origin. The choice of data windows made of the observations relative to six consecutive observation times, that is the choice of 6 months data windows, is motivated by the fact that several numerical experiments have shown that the estimates of the parameter vector Θ obtained from the calibration remain substantially unchanged when we use in the calibration data corresponding to data windows made of the observations relative to 12, or 24 consecutive observation times. The solution of a calibration problem using the data corresponding to a window of six consecutive observation times requires about 1 min of CPU time on a Centrino Duo Intel Personal Computer using a Fortran 90 code. However, the 206 calibration problems considered here are independent from the others and can be solved in parallel when adequate computing resources are available (for example, they can be solved in parallel on the ENEA grid). That is, the CPU time required to solve the 206 calibration problems that use a 6 months data window as data is approximately 206 min on 1 processor, or 1 min on 206 processors.

The data analysis presented in this section investigates two problems. The first one consists of understanding if the calibration procedure described in Section 2 to determine the value of the vector Θ, that is, the procedure used to solve the maximum likelihood problem (6), gives values of Θ that are really associated with the data time series, that is, values of Θ that are not an artefact of the computational procedure used to determine them. The second one, to be faced only if the first one is solved positively, is the problem of evaluating the ability of these estimated values of Θ of forecasting the values of x_t, z_t in the future, that is the ability of forecasting using the model (1–3) and formulae (14) and (15) the values x_t and z_t relative to observation times posterior to the observation times contained in the data window used to estimate the vector Θ. This ability is evaluated a priori (‘model implied’) using formula (20) and established a posteriori (‘empirically’) comparing the forecasted values to the observations actually made.

As said previously, we have solved 206 calibration problems relative to the 206 data windows described above determining 206 values of the vector Θ. In the solution of the 206 maximization problems (6) we have chosen the initial guess of the maximization procedure to be always the same and in the stopping criterion (10), we have chosen δ₁ = 5 × 10⁻⁴ and k_max = 10,000. The choice of the initial guess is made exploiting the following information:

a.	the standard deviation of the time series of log-returns of xt and zt to choose the initial guesses of the stochastic variance , of the volatility of volatility ε and of the parameter γ appearing in Equation (2);
b.	the time series of the ratio , i = 1, 2, …, 210, to choose the initial guess of β;
c.	the empirical correlation between the time series ΔIx,i, ΔIz,i, i = 1, 2, …, 210, to choose the initial guess of the correlation coefficient ρ1,3. The magnitude of the initial guesses of the correlation coefficients ρ1,2, ρ2,3 is chosen to be of the order 10−2.

Figures 1–3 show (in ordinate) the components of the vector Θ obtained solving the maximum likelihood problem (6), as a function of i, the value of the index of the last observation time contained in the data window used in the calibration (in abscissa). That is, the vector Θ obtained using a given data window is associated with the index of the last observation time of the data contained in the window. Let Θ*^,i be the vector Θ obtained solving problem (6) using the 6 months data window ending at time , i = 5, 6, …, 210. Figures 1–3 show that, as a function of i, the parameters ε, γ, the initial stochastic variance and the correlation coefficients ρ_1,2 and ρ_2,3 appear to be approximately given by piecewise constant functions. In particular, two observation times (the black bars in Figures 1–3) where the piecewise constant functions jump are evidenced, the first one after approximately the first year of observation (that is around 31 October, 1990) and the second one after approximately 11 years of observation (that is around 31 October, 2000). That is, the data analysis carried out and illustrated in Figures 1–3 shows that roughly speaking the data can be divided into three periods:

•	Period 1: this period (from the beginning of the time series up to the first black bar) is very small and goes from 31 December, 1989 to 31 October, 1990;
•	Period 2: this period (between the first and the second black bar) is quite long and goes from 30 November, 1990 to 31 October, 2000;
•	Period 3: this period (after the second black bar until the end of the time series) goes from 30 November, 2000 to 30 June, 2007.

That is, roughly speaking, Figures 1–3 show that the vectors Θ determined by the calibration procedure can be considered approximately constants in each one of these three periods.

Note that the values of the initial stochastic variance obtained from the solution of the calibration problems are approximately constant over Period 1. This is probably due to the fact that monthly data are considered so that the micro structure of the variance is lost. Indeed, it is possible that the estimates of obtained are of low quality. This is due to the fact that is a parameter whose calibration is difficult. In 10,11 we have already faced the difficulty of estimating the initial stochastic variance when we have studied the calibration problem for the Heston model. We remark that in 15 the initial stochastic variance is not estimated together with the other parameters of the model as we do here. In fact in 15 the Black–Scholes implied volatility and the adjusted integrated volatility are used to estimate the initial stochastic variance.

We remark that Figure 3 shows that the correlation coefficient ρ_1,3 that measures the correlation between the stochastic differentials present in the equation of the log-return of the S&P 500 index and one of the stochastic differentials present in the equation of the log-return of the HFRI-Equity hedge fund index is almost constant and approximately equal to one over the entire observation period. This fact seems to confirm the validity of model (1–3) which assumes that the behaviour of the HFRI-Equity hedge fund index is strongly related to the behaviour of the S&P 500 index. Furthermore, the fact that the parameter β is substantially constant (exception made when we go from Period 1 to Period 2 when β goes approximately from 0.5 to 0.7) confirms the assumption of the existence of a kind of ‘proportionality’ between the variations of the log-returns of the HFRI-Equity hedge fund index and of the S&P 500 index.

Let us study the bias of the estimates , j = 1, 2, …, 206, solutions of the maximum likelihood problem (6) on some time windows chosen as representatives of the data time series. We use the bootstrap method proposed in 16 to generate new sample ‘data’. To fix the ideas we consider 5–6 months data windows: the first one falls in the first period (months 1–6 of the data time series), the second one falls between the first and the second period (months 10–15 of the data time series), the third one falls in the second period (months 70–75 of the data time series), the fourth one falls between the second and the third period (months 138–144 of the data time series), and the last one falls in the third period (months 190–195 of the data time series). The results obtained in these data windows represent the results obtainable with a more systematic analysis of the data time series. We use as reference estimate of the vectors Θ, , in the window j, j = 1, 2, …, 5, the solution of the maximum likelihood problem (6) (see 1). Note that we have: , , , , . Let N_R be a positive integer, to measure the bias of the corresponding estimators we generate N_R replicas of the observed data in each window and we estimate the vectors Θ relative to these sets of replicated data. That is, for j = 1, 2, …, 5, in the window j, a sample Θ^j,k, k = 1, 2, …, N_R is generated by solving the maximum likelihood problem (6) with the replicas of the observed data and the relative bias: (32) We consider N_R = 100 and N_R = 1000. Tables 1–4 show the values of the relative bias , j = 1, 2, …, 5, of the estimated parameters. Moreover let , k = 1, 2, …, N_R, j = 1, 2, …, 5, i = 1, 2, …, 10, be the relative errors of the components of the estimated vectors. For i = 1, 2, …, 10, j = 1, 2, …, 5, we compute the standard deviation of these samples. For j = 1, 2, …, 5, Table 5 shows the mean (over i, i = 1, 2, …, 10) of these standard deviations and the biggest of these standard deviations with the corresponding parameter name. The relative bias shown in Tables 1–4 for most of the parameters is satisfactorily small. In fact, the phenomenological character of the model that we are considering suggests that it is dubious to pretend very accurate results.

Table 1. Relative bias of the parameter estimators in the five windows (N_R = 100).

Window period		bχ	bε	bθ	bβ	bγ
Window 1	0.12838	0.000285	0.2080	0.39624	0.12838	0.2806
Window 2	0.00335	0.000051	0.02406	0.00355	0.00909	0.00263
Window 3	0.000417	0.00059	0.00545	0.01772	0.0668	0.108
Window 4	0.0233 × 10^−3	0.00283 × 10^−3	0.14 × 10^−3	0.45 × 10^−3	0.0111	0.0134
Window 5	0.000022	0.0000096	0.0000911	0.00058	0.000132	0.00273

Table 2. Relative bias of the correlation coefficients and of the initial stochastic variance in the five windows (N_R = 100).

Window period	bρ1,2	bρ1,3	bρ2,3
Window 1	0.09126	0.00779	0.0709	0.4903
Window 2	0.000918	0.00049	0.00179	0.0256
Window 3	0.000865	0.0035	0.00019	0.0113
Window 4	0.285 × 10^−5	0.38 × 10^−3	0.55 × 10^−3	0.00176
Window 5	0.594 × 10^−5	1.71 × 10^−3	0.45 × 10^−5	0.00023

Table 3. Relative bias of the parameter estimators in the five windows (N_R = 1000).

Window period		bχ	bε	bθ	bβ	bγ
Window 1	0.0066	0.0001	0.00543	0.1133	0.0277	0.0659
Window 2	0.000025	0.00002	0.0077	0.0142	0.0011	0.00005
Window 3	0.000005	0.0006	0.00045	0.0163	0.0572	0.1536
Window 4	0.000011	0.000005	0.000128	0.00365	0.00627	0.0153
Window 5	0.000026	0.00001	0.000087	0.000628	0.00017	0.0028

Table 4. Relative bias of the correlation coefficients and of the initial stochastic variance in the five windows (N_R = 1000).

Window period	bρ1,2	bρ1,3	bρ2,3
Window 1	0.0220	0.0092	0.0173	0.1388
Window 2	0.0003	0.00026	0.00012	0.01002
Window 3	0.00012	0.00615	0.000202	0.00971
Window 4	0.0000214	0.000628	0.000065	0.001303
Window 5	0.0000065	0.00177	0.0000063	0.0002546

Table 5. Mean of the standard deviations of the relative errors of the components of the estimated vectors and worst standard deviation and parameter where it occurs (N_R = 1000).

Window	Mean SD	Worst SD (parameter)
Window 1	0.0476	0.12 (), 0.09 (γ, θ)
Window 2	0.0189	0.04 (), 0.05 (θ)
Window 3	0.0410	0.239 (γ), 0.1 (β)
Window 4	0.0149	0.074 (γ), 0.035 (β)
Window 5	0.00061	0.0026 (γ), 0.002 (β)

We propose a second way of studying the bias of the estimated values of the vector Θ. We divide the 206 estimates of Θ obtained solving the 206 calibration problems in three sets. The first set, named Set 1 (relative to Period 1), corresponds to the estimates of Θ obtained using the first 13 data windows, the second one, named Set 2 (relative to Period 2), corresponds to the estimates of Θ obtained using the data windows that go from the 14th to the 130th data windows and the last one, named Set 3 (relative to Period 3), collects the estimates of Θ obtained using the data windows that go from the 131th to the 206th data windows. From these sets we proceed as follows. Let us consider, for example, Set 2. We further divide the elements of Set 2 into groups of estimates coming from disjoint data windows. Note that this procedure is applied only to Sets 2 and 3; in fact, Set 1 has too few elements to work with to make sense out of this procedure. We take as reference estimate of the vector Θ the mean value of Θ over a subset of disjoint 6 months data windows extracted from Sets 2 and 3. Tables 6 and 7 show quantities similar to those shown in Tables 1–4 obtained using these means as reference estimates of Θ and the solutions of the calibration problems as samples to evaluate the bias.

Table 6. Relative bias of the parameter estimators in Set 2 (Period 2) and Set 3 (Period 3).

Set		bχ	bε	bθ	bβ	bγ
Set 2	0.107	0.0114	0.0004	0.0001	0.0016	0.0077
Set 3	0.112	0.0087	0.0088	0.0002	0.0159	0.0051

Table 7. Relative bias of the correlation coefficients and of the initial stochastic variance in Set 2 (Period 2) and Set 3 (Period 3).

Set	bρ1,2	bρ1,3	bρ2,3
Set 2	0.0119	0.0082	0.0593	0.0067
Set 3	0.0077	0.004	0.0346	0.006

We note that the two procedures to study the bias are different. First of all, the first procedure uses replicated data, that is, a kind of synthetic data, while the second procedure uses only observations. That is, the ‘replicas’ are obtained starting from observations made in different time periods. Moreover, the first procedure measures the bias of the estimate in each window taking as reference estimate the value of the vector Θ obtained solving the calibration problem using as data the (real) observations made in that window. The second procedure measures the bias choosing as reference estimate the mean value of the optimal vectors Θ* computed using as data a subset of disjoint data windows contained in Period 2 and Period 3. Indeed, this second choice of the reference estimate has a negative effect on the magnitude of the bias obtained for the parameters whose value is not really constant during the time period considered. In fact this choice gives good results for the parameter χ in Period 2, and for the parameters ε, θ and γ in Period 3 (Figure 1). The same choice is not well-suited for the parameters , , ρ_2,3 (Figures 2 and 3) and we can expect these parameters to be biased. We observe that when we use in the second procedure to estimate the bias the mean over the components i = 1, 2, …, 10 of the standard deviations of the relative errors considered in Table 5 is 0.0620 in Period 2 and 0.0611 in Period 3. In both periods, the parameter having the largest standard deviation is μ (about 25%) followed by the parameters ρ_2,3 (about 20%) and γ (about 5%) in Period 2 and in Period 3 by ρ_2,3 (about 8%) and (about 5%).

The first procedure to estimate the bias, based on replicated data, does not suffer from the previous effect since the time window of 6 months is a reasonable time interval where all the parameters are constant. Note that Tables 1–5 show that the estimates of the initial stochastic variance and of the parameter γ are biased since in the last three windows, the relative bias does not decrease when N_R increases.

We can conclude that the data analysis carried out by solving the 206 maximum likelihood problems associated with the observation windows considered previously shows a convincing evidence of the fact that the values of the vector Θ determined by the maximum likelihood procedure are really associated with the data time series and supports some of the assumptions made to build model (1–3). That is, the results of the data analysis presented solve in the affirmative the first problem posed.

The second problem posed to our data analysis is the investigation of the quality of the forecasted values of the log-returns of the indices obtained using the model (1–3) and the values of Θ determined solving the calibration problem shown in Figures 1–3. That is, we use the values of the vectors Θ determined solving the maximum likelihood problem and formulae (14) and (15) to forecast the values of the log-returns and and of the increments of the HFRI-Equity index , i = 5, 6, …, 210 − m, m = 1, 2, …, 6, that is, 1 month, 2 months, … up to 6 months in the future. Recall that here ‘future’ means the time after the last observation time contained in the data window used to estimate the vector Θ.

Let N_tot be a positive integer that denotes the number of forecasted values m months in the future of returns of the S&P 500 index and of the HFRI-Equity index used in this study. Note that below we will choose N_tot independent of m, m = 1, 2, …, 6. The forecasted values are compared with the historical data and the following quantities have been defined to measure the accuracy of the forecasted values: (33) where quantities , , are given by (34) (35) The quantities , , are the observed values (real data) and the quantities , , are the corresponding m months in the future forecasted values and , j = 1, 2, …, m, are the variations of the index I_z,4+i+j−1 computed using the forecasted values , i = 1, 2, …, N_tot, m = 1, 2, …, 6. Finally, we have computed the mean value of the quantities , i = 1, 2, …, N_tot, that is , m = 1, 2, …, 6.

In Table 8 we show the values of the quantities ε_x,m, ε_z,m, ε_var,m and s_m, as a function of the forecasting period, m = 1, 2, …, 6 (1, 2, …, 6 months in the future), when we consider N_tot = 200 observation times.

Table 8. Quality of the forecasted values of the log-returns x_t and z_t and of the forecasted increment of the hedge fund index established comparing with historical data.

Forecasting period m	εx,m	εz,m	εvar,m	sm
1 month	0.1271	0.0214	0.0202	0.0217
2 months	0.1739	0.0332	0.0327	0.0365
3 months	0.1976	0.0397	0.0435	0.0499
4 months	0.2226	0.0478	0.0530	0.0631
5 months	0.2425	0.0577	0.0633	0.0770
6 months	0.2967	0.0616	0.0715	0.0907

We note that the quantities ε_x,m, ε_z,m are the mean values of the relative errors committed on the forecasted values m months in the future of the returns x_t and z_t of the S&P 500 index and of the HFRI-Equity index, respectively, and that ε_var,m is the mean value of the absolute errors committed on the forecasted values m months in the future of the HFRI-Equity index I_z,t = e^z_t, m = 1, 2, …, 6.

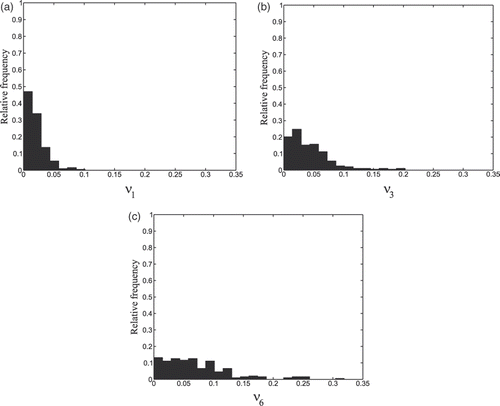
Finally, we show the histograms of the absolute errors committed on the quantities a_t,m, that is, the histograms of the values taken by the function ν_m(t) = |a_t,m − â_t,m|, , i = 1, 2, …, N_tot, m = 1, 3, 6 (Figure 4).

Figure 4. Histogram of the values taken by (a) ν₁, (b) ν₃ and (c) ν₆.

We conclude this section by showing the values forecasted using formulae (11) and (12) of the log-return x_t of the S&P 500 index, and of the log-return z_t of the HFRI-Equity index 1 month, 3 months and 6 months in the future (stars) and the corresponding historical data (squares) on a period covering 204, 202 and 198 months, respectively (Figures 5–7).

Figure 5. Forecasted values of the S&P 500 x_t (a) and of the HFRI-Equity z_t (b) 1 month in the future (*) and historical data of the log-return of the indices (□).

Figure 6. Forecasted values of the S&P 500 x_t (a) and of the HFRI-Equity z_t (b) 3 months in the future (*) and historical data of the log-return of the indices (□).

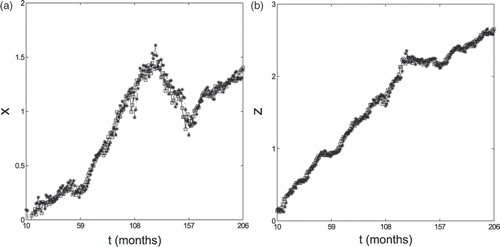
Figure 7. Forecasted values of the S&P 500 x_t (a) and of the HFRI-Equity z_t (b) 6 months in the future (*) and historical data of the log-return of the indices (□).

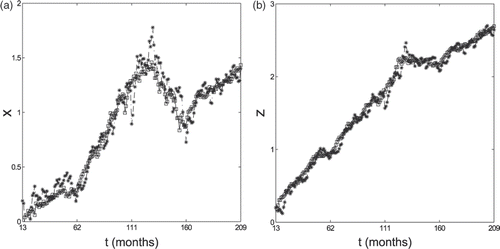
We note that, as expected, the quality of the forecasts of the returns of x_t and z_t degrades when we look further into the future, that is, for example, the forecasted values 1 month in the future are of higher quality than the forecasted values 6 months in the future. However, the forecasted values of z_t 6 months in the future are somehow satisfactory. In particular, we can say that our forecasts seem more reliable when compared to the forecasts obtained by traditional (multi)regression methods (these last ones do not have very high R² (determination coefficient) for hedge indices, in fact for the linear regression between HFRI-Equity and S&P 500, with our monthly data, R² is only 0.44). Moreover, when we consider 3 and 6 months in the future the forecasted values of HFRI-Equity index are of higher quality than S&P 500 ones. Recall that independently from equity movements, the relationship between HFRI-Equity and S&P 500 is stable (in the time period considered), with a constant β around 0.5–0.7. This is the case even if in the 3–6 months time periods of the forecasts is more likely that the market conditions have changed and that, therefore, the model parameters resulting from the calibration must be changed.

Obviously, it is not scientifically proved that the stability of this relationship remains true in totally different time contexts; however, its observed stability in this huge time period (1990–2007) leads us to consider it for strategic allocation choices. Each qualitative forecast about S&P 500, elaborated by the investment department of an asset management firm, according to macroeconomic convictions, can be translated in allocation decisions for long/short equity strategy, particularly to 6 months periods. Just because it is very difficult to determine macro scenario on this time horizon, the possibility of using a (demonstrated) stable relationship can be considered as an useful guide in the investments. This is even more important if we consider that in the hedge funds universe, statistically, only investments for medium/long period are satisfying in terms of performance, while a more tactical point of view is usually less gratifying.

Let us now try to establish the quality of the forecasts a priori (‘model implied’), that is, before comparing with the historical data.

Table 9 shows the observations and the forecasted values corresponding to the first 46 observation times. A complete table relative to the entire data time series is contained at the website: http://www.econ.univpm.it/recchioni/finance/w8.

Table 9. The first 46 monthly data and the forecasted values of the log-returns of the HFRI-Equity index 1 month and 6 months in the future compared with the historical data of the 1 month log-return and of the 6 months log-return .

i	Date	1 month variation of the S&P 500 index ΔIx,i (%)	1 month variation of the HFRI–Equity index ΔIz,i (%)	Observed 1 month return	Forcasted 1 month return	Observed 6 months return	Forecasted 6 months return
1	31/01/1990	−6.88	−3.34
2	28/02/1990	0.85	2.85
3	31/03/1990	2.43	5.67
4	30/04/1990	−2.69	−0.87
5	31/05/1990	9.20	5.92
6	30/06/1990	−0.89	2.52	2.52E-02	6.55E-03
7	31/07/1990	−0.52	2.00	2.00E-02	1.18E-02
8	31/08/1990	−9.43	−1.88	−1.88E-02	1.10E-02
9	30/09/1990	−5.12	1.65	1.65E-02	4.48E-03
10	31/10/1990	−0.67	0.77	7.70E-03	6.66E-03
11	30/11/1990	5.99	−2.29	−2.29E-02	2.33E-03	2.694E-02	3.993E-02
12	31/12/1990	2.48	1.02	1.02E-02	1.63E-03	1.191E-02	7.308E-02
13	31/01/1991	4.15	4.90	4.90E-02	−2.97E-03	4.068E-02	6.786E-02
14	28/02/1991	6.73	5.20	5.20E-02	3.42E-03	1.158E-01	2.717E-02
15	31/03/1991	2.22	7.22	7.22E-02	6.43E-03	1.769E-01	4.062E-02
16	30/04/1991	0.03	0.47	4.70E-03	2.00E-02	1.734E-01	1.409E-02
17	31/05/1991	3.86	3.20	3.20E-02	1.53E-02	2.393E-01	9.814E-03
18	30/06/1991	−4.79	0.59	5.90E-03	1.64E-02	2.341E-01	−1.766E-02
19	31/07/1991	4.49	1.41	1.41E-02	2.28E-02	1.930E-01	2.071E-02
20	31/08/1991	1.96	2.17	2.17E-02	5.36E-03	1.586E-01	3.921E-02
21	30/09/1991	−1.91	4.30	4.30E-02	6.54E-03	1.271E-01	1.262E-01
22	31/10/1991	1.18	1.16	1.16E-02	1.34E-02	1.348E-01	9.517E-02
23	30/11/1991	−4.39	−1.08	−1.08E-02	1.18E-02	8.777E-02	1.026E-01
24	31/12/1991	11.16	5.02	5.02E-02	1.00E-02	1.357E-01	1.445E-01
25	31/01/1992	−1.99	2.49	2.49E-02	1.48E-02	1.478E-01	3.261E-02
26	29/02/1992	0.96	2.90	2.90E-02	1.72E-02	1.560E-01	3.990E-02
27	31/03/1992	−2.18	−0.28	−2.80E-03	1.35E-02	1.052E-01	8.335E-02
28	30/04/1992	2.79	0.27	2.70E-03	1.06E-02	9.548E-02	7.318E-02
29	31/05/1992	0.10	0.85	8.50E-03	1.59E-02	1.169E-01	6.176E-02
30	30/06/1992	−1.74	−0.92	−9.20E-03	8.66E-03	5.369E-02	9.231E-02
31	31/07/1992	3.94	2.76	2.76E-02	4.94E-03	5.646E-02	1.079E-01
32	31/08/1992	−2.40	−0.85	−8.50E-03	4.88E-03	1.796E-02	8.346E-02
33	30/09/1992	0.91	2.51	2.51E-02	4.50E-03	4.644E-02	6.531E-02
34	31/10/1992	0.21	2.03	2.03E-02	4.80E-03	6.481E-02	9.928E-02
35	30/11/1992	3.03	4.51	4.51E-02	4.37E-03	1.035E-01	5.308E-02
36	31/12/1992	1.01	3.38	3.38E-02	1.22E-02	1.513E-01	3.001E-02
37	31/01/1993	0.70	2.09	2.09E-02	1.30E-02	1.438E-01	2.966E-02
38	28/02/1993	1.05	−0.57	−5.70E-03	1.90E-02	1.471E-01	2.731E-02
39	31/03/1993	1.87	3.26	3.26E-02	1.22E-02	1.555E-01	2.913E-02
40	30/04/1993	−2.54	1.30	1.30E-02	1.62E-02	1.472E-01	2.654E-02
41	31/05/1993	2.27	2.72	2.72E-02	1.18E-02	1.275E-01	7.539E-02
42	30/06/1993	0.08	3.01	3.01E-02	1.04E-02	1.235E-01	8.066E-02
43	31/07/1993	−0.53	2.12	2.12E-02	1.36E-02	1.238E-01	1.195E-01
44	31/08/1993	3.44	3.84	3.84E-02	1.54E-02	1.737E-01	7.566E-02
45	30/09/1993	−1.00	2.52	2.52E-02	1.75E-02	1.653E-01	1.015E-01
46	31/10/1993	1.94	3.11	3.11E-02	1.84E-02	1.861E-01	7.300E-02

Note that in Table 9 some values are highlighted in bold font. These values are some of the most satisfactory forecasted values of the returns a_t,m, 1 month and 6 months in the future when compared with historical data. We have computed the conditioned variance of the state variable z_t (formula (20)) that is, the conditioned variance of the forecasted values of the returns the HFRI-Equity index. We have found that the conditioned variances relative to the forecasted values of the returns 1 month and 6 months in the future marked in bold font in Table 9 are significantly smaller than the remaining conditioned variances. For example, while the mean value of the conditioned variances of the forecasted values of the returns of the HFRI-Equity index 1 month in the future is 1.27 × 10⁻² the values of the conditioned variances of the forecasted values marked in bold (in time order) are 7.4 × 10⁻³, 4.4 × 10⁻³, 6.1 × 10⁻³, that is, the conditioned variance of the bold forecasts is reduced by approximately a factor 0.5 with respect to the mean value. Note that we have variances smaller than 4.4 × 10⁻³ only 1 time in the historical series of the variances and that this smallest value is 4.8 × 10⁻⁴. The same happens in the case of the forecasted values 6 months in the future where the mean value of the conditioned variances is 2.5 × 10⁻² and the conditioned variances of the forecasted values marked in bold font (in time order) are 9.94 × 10⁻³, 9.96 × 10⁻³, 1.18 × 10⁻² and 1.23 × 10⁻². That is, also in this last case the conditioned variances of the forecasted values marked in bold is reduced by approximately a factor 0.5 of the mean value. Finally, we note that the smallest variance in the historical series of the conditioned variances of the 6 months in the future forecasted values is 87.81 × 10⁻⁴ and all the remaining values in the time series are greater than 9.94 × 10⁻³. We can conclude that the value of the conditioned variance allows us to assign ‘a priori’ (‘model implied’) a degree of reliability to the forecasted values, that is, a small conditioned variance corresponds to a great degree of reliability of the forecasted values and this is confirmed by the comparison with the historical data. This fact may be of great relevance in practical situations since by using the conditioned variances we can evaluate a priori the quality of the forecasts of returns of the HFRI-Equity index. A similar analysis can be carried out for the forecasts of returns of the S&P 500 index obtaining similar results.

4. Conclusions

The results contained in this article show that models made of stochastic differential equations can be used to solve well-known statistical and econometric problems. Moreover, the proposed stochastic differential model appears to work well also on relatively small data time windows possibly because the model has captured some relevant features of the data. The forecasts obtained from the model seem to be of high quality. In fact, as remarked in Section 3, these forecasts seem to be more accurate than those obtained by traditional (multi)regression methods.

Finally, the data analysis presented suggests several possible directions of future research. We mention only one of them. We remark that the previous analysis shows that the forecasts of the returns of the HFRI-Equity index are more accurate than those of the S&P 500 index. This fact suggests the idea of introducing a new stochastic model (not necessarily the Heston model) to describe the dynamics of the log-return of the HFRI-Equity index and then of trying to use the dynamics of the HFRI-Equity index to describe the dynamics of the S&P 500 index. Indeed, since the variation of the HFRI-Equity index is smoother than the variation of the S&P 500 index, it should be easier to find ‘ad hoc’ stochastic models of the HFRI-Equity index instead of modelling directly the behaviour of the S&P 500 index. This new model corresponds to the inversion of the cause–effect relation that has been used in the work of Pillonel and Solanet 9 and in the model proposed in 1, and was used here to describe the relation between the market and the hedge fund indices.

In the website http://www.econ.univpm.it/recchioni/finance/w8, we show the forecasted values of the indices I_x,t and I_z,t compared with the historical data and we provide some animations relative to the forecasting experiment during the complete observation period.

Acknowledgements

The numerical experiment reported in this article has been performed using the computing grid of ENEA (Roma, Italy). The support and sponsorship of ENEA are gratefully acknowledged.

Appendix

As shown in 1 (arguing as done in [17, p. 605] for the Heston stochastic volatility model) an explicit formula of the fundamental solution p_f (x, z, v, t, x′, z′, v′, t′|Θ), (x, z, v), (x′, z′, v′) ∈ ℝ × ℝ × ℝ⁺, t, t′ > 0, t − t′ > 0, of the Fokker–Planck equation associated with the system of stochastic differential Equations (1–3) can be derived, that is (36) where ι denotes the imaginary unit, I_ν(z), z ∈ ℂ, is the modified Bessel function of positive real order and (37) (38) (39) (40) (41) (42) (43)

Let us give the formulae derived in 1 that is needed to implement the computational method used to evaluate (8). Letting V, L, K, E be positive real numbers, we use the following formulae: (44) where (45) and (46) We recall that τ_i+1 = t_i+1 − t_i, i = 0, 1, …, n − 1, and that . For i = 1, 2, …, n, the procedure to approximate the integrals (45) and (46) is based on an expansion in powers of τ_i, as τ_i goes to zero, (see 1, Section 3 for further details). The first-order approximation in τ_i gives the following formula: (47) where is given by (48) where m* is a positive integer (see 1), p_1,1 = 1, p_2,1 = −0.44721359549996, p_3,1 = −1.3416407864998, the quantity μ(k, ξ) is given by formula (37), and the quantities d_j,m,ζ, j = 1, 2, 3, m = 0, 1, …, m*, ζ = 0, 1, …, 4^m − 1, are given by (49) (50) where α(k, ξ, τ) is given by (51) Note that the quantities defined in (49) and (50) are the coefficients of a truncated wavelet expansion of the function e^{−α(k,ξ,τ)v′}, and that when (k, ξ) = (0, 0) these expressions are not well-defined. However, it is easy to see that when (k, ξ) = (0, 0) the values of (49) and (50) can be determined with some elementary manipulations of the formulae written above. The index m* is a parameter that tells where the wavelet expansion has been truncated.

We note that using the fast Fourier transform algorithm the computational cost of evaluating formula (47) on a suitable grid of N_λ points in the λ variable using R points to discretize the integrals in the k and ξ variables is O(2R² + 2N_λ log N_λ), as R and N_λ go to infinity, where O(·) is the Landau symbol. This reduces dramatically the cost associated with a naive approach (an approach that does not take advantage of the fast Fourier transform algorithm) that we indicate as being , as R and N_λ go to infinity.