Bayesian inversion by parallel interacting Markov chains

Abstract

Markov chain Monte Carlo (MCMC) methods are known to produce samples of virtually any distribution. They have already been widely used in the resolution of non-linear inverse problems where no analytical expression for the forward relation between data and model parameters is available, and where linearization is unsuccessful. However, in Bayesian inversion, the total number of simulations we can afford is highly related to the computational cost of the forward model. Hence, the complete browsing of the support of the posterior distribution is hardly performed at final time, especially when the posterior is high dimensional and/or multimodal. In the latter case, the chain may stay stuck in one of the modes. Recently, the idea of making several Markov chains interact at different temperatures has been explored. These methods improve the mixing properties of classical single MCMC. Furthermore, these methods can make efficient use of large central processing unit (CPU) clusters, without increasing the global computational cost with respect to classical MCMC.

Keywords:

• inverse problem
• Bayesian inversion
• MCMC
• interacting Markov chains
• tempering
• history matching

1. Introduction

Monte Carlo methods are becoming increasingly important for the solution of non-linear inverse problems. Typically, the inverse problem is formulated as a search for solutions fitting the data within a certain tolerance, given by data uncertainties. In a non-probabilistic setting this means that we search for solutions with calculated data whose distance from the observed is less than a fixed, positive number. In a Bayesian context, the tolerance is soft: a large number of samples of statistically near-independent models from the a posteriori probability distribution are sought. Such solutions are consistent with data and prior information, as they fit the data within error bars, and adhere to soft prior constraints given by a prior probability distribution.

Precisely, we consider the study of a system X ∈ 𝒳, on which we have an indirect measurement d, that is function of the state of X, modelled by F(X), and some a priori information under the form of the prior distribution ℙ(X). We also consider that the measurement d is affected by an error and that we know how to simulate F up to an approximation error, both errors being accounted for by ℙ(d|X). We also define the joint distribution ℙ(d, X). Then, assuming that all these distributions admit a density with respect to the Lebesgue measure, denoted f(·), the conditional density of X with respect to d takes the following form: (1) This is the Bayesian formulation of inverse problem and ℙ(X|d), whose density f (X|d), is the posterior distribution, see 1. The formula (1) shows that this problem can be viewed as a classical statistical inference problem, where we want to sample independent realizations from the posterior distribution. Note that the normalization constant in (1) is generally intractable in high-dimensional problems. Therefore, we consider that the posterior is known up to a constant, being defined from the prior knowledge on the system studied and the data with its associated measurement error.

There exists several methods for solving (1) such as the Kitanidis–Oliver algorithm 2,3, developed for petroleum engineering applications and the neighbourhood algorithm 4,5, developed for geophysical inverse problems. In spite of its universality the speed of convergence of the first one is controversial: it consists in performing a large number of optimizations with an observed datum perturbed according to its measurement error. It is particularly difficult to know how many optimizations should be performed. The second one seems to be limited for low-dimensional problems: it can be seen as a geometric version of an iterated importance sampling scheme (see, e.g. 6, chapter 14). This article focusses on Markov chain Monte Carlo (MCMC) methods for their universality and the relative ease of their implementation.

MCMC methods suit this problem particularly well, as they are known to produce samples of virtually any posterior distribution. Two problems may arise then. On the one hand, the dimension of the problem may be so large that the chain has to be run for an intractable number of iterations to converge and to achieve an efficient sampling of the posterior, we say that they have weak mixing properties. On the other hand, an evaluation of the forward operator F can be very computationally demanding so that the practitioner wishes to minimize the number of iterations. Moreover, when the posterior has several disconnected modes in a high-dimensional space, which is often the case in non-linear Bayesian inversion, the problem of exploring the whole support of the posterior is a difficult one. It can be shown that even for very simple problems most classical Markov chain algorithms can fail at identifying the main modes of the posterior, because of their lack of mixing 7.

We expose a method to improve the global efficiency of the Markov chain by generating a collection of chains in parallel at different temperatures and allowing them to interact. This method is not more computationally demanding than classical MCMC since it can be easily parallelized.

This article aims at providing researchers and engineers with some methods for applying interacting MCMC methods. Thus, it begins in Section 2 with basics for MCMC methods, some examples of classical algorithm and earlier attempts to improve mixing properties like annealing and tempering techniques, which rely on the same basic principles as interacting MCMC techniques, exposed in Section 3. In Section 4, we will show an application to a reservoir engineering problem. This article ends with some conclusions and perspective of future work.

2. MCMC methods

MCMC, introduced by Metropolis et al. 8, is a popular method for generating samples from virtually any distribution π defined on (𝒳, ℬ(𝒳)), where ℬ(𝒳) stands for the Borel sets of 𝒳. In particular there is no need for the normalizing constant of π to be known and the space 𝒳 ⊆ ℝ^d (for some integer d) on which it is defined can be high dimensional. We recall here some classical results on MCMC methods. For a comprehensive review of MCMC, see 6, chapters 6–13. For a more detailed account on Markov chains theory, see 9.

2.1. Principles

The method consists in simulating an ergodic Markov chain {X_n, n ≥ 0} on 𝒳 with transition probability P such that π is a stationary density for this chain, i.e. ∀A ∈ ℬ(𝒳) (2) Such samples can be used for example, to compute integrals (3) estimating this quantity by (4) for some h : 𝒳 → ℝ. A very useful concept in constructing ergodic Markov chains is reversibility. A Markov chain is reversible if it satisfies the detailed balance condition: (5) This means that, if started in stationarity, the Markov chain has the same chance of starting at x and jumping to y as starting at y and jumping to x.

We illustrate the principles of MCMC with the Metropolis–Hastings (MH) update. It requires the choice of a proposal distribution q. The role of q consists in proposing potential transitions for the Markov chain. Given that the chain is currently at x, a candidate y is accepted with probability α(x, y) defined as (6) Otherwise, it is rejected and the Markov chain stays at its current location x. The transition kernel P of this Markov chain takes the form, for (x, A) ∈ 𝒳 × ℬ(𝒳) (7) The Markov chain defined by P is reversible with respect to π and therefore admits π as invariant distribution. Conditions on the proposal distribution q that guarantee irreducibility and positive recurrence are easy to meet and many satisfactory choices are possible.

2.2. Some examples of MH samplers

The arbitrariness of the choice of q(x, ·) allows considerable freedom to design a multitude of different chains, each with stationary distribution π, although in the Bayesian inversion framework, q should rely on the a priori distribution. Some examples include (see 6, chapter 7, for more examples):

1.	the independent sampler (IMH): q(x, y) = q(y), where q is generally the prior in Bayesian inversion,
2.	the symmetric increments random-walk sampler (SIMH): q(x, y) = q(|y − x|), where q can be a zero-mean version of the prior,
3.	the Langevin sampler (LMH): assuming that π is differentiable on 𝒳, it allows to take advantage of the gradient information to give the sampling direction, q takes the form: (8) where h is a parameter to choose according to e.g. 10 or 11. Note that a bad choice of h can induce erratic behaviour of the chain,
4.	the adaptive algorithm of 12 (ASIMH): In this algorithm, y is proposed according to qθn(x, ·) = 𝒩(x, Γn), where θ = (μ, Γ). We also consider a non-decreasing sequence of positive step sizes {γn}, such that and for some δ > 0. In practice, we generally use: γn = 1/n, as suggested in 12. The parameter estimation algorithm takes the following form: (9)
5.	the Gibbs sampler: Here 𝒳 = 𝒳1 × ··· × 𝒳d, and q = qi leaves all coordinates fixed except the i-th one, which it proposes according to the conditional distribution (xi|{xj}j≠i). This implies that α(x, y) = 1 for all x and y, so there are no rejections. If the resulting i-th component Gibbs sampler is called Pi, then these components can be combined to yield the random-scan Gibbs sampler which is the average , or the deterministic-scan Gibbs sampler which is the product PDU = P1 … Pd.

2.3. Comments

One of the problems with MH algorithms is the abundance of choice available for choosing the proposal distribution q(x, ·). For instance even if the type of algorithm (perhaps the SIMH) has been chosen, it is necessary to scale the proposal variance to be appropriate for π(·). Such a problem is known as a scaling problem. To make this question more concrete, consider the following problem. Suppose that q(x, ·) is distributed as the d-dimensional normal distribution 𝒩(x, σ²I_d), for some σ² > 0. We recall that the acceptance probabilities for this algorithm are given by (6). For very small values of σ², small jumps are attempted by the algorithm, and because of the form of (6), these moves are almost always accepted. The Markov chain mixes very slowly because its increments are so small. On the other hand, if σ² is chosen to be very large, long distance jumps are attempted by the algorithm, most of which are rejected. The algorithm therefore spends long period of time in the same state, and thus the algorithm still converges slowly. For this problem, ‘very large’ and ‘very small’ have to be interpreted in a way related to the particular form of π. It seems reasonable that ‘moderate’ values of σ² should be preferred. However, it is difficult to see how to figure out what values are ‘moderate’, especially if π is very complicated. In Bayesian inversion context, the random walk type algorithms, like the SIMH or the LMH, generally fail at identifying different modes. In large dimensional space, the scaling factor generally has to be ‘small’ so as to get an acceptable acceptance rate (6). Therefore, these two algorithms perform generally a local exploration and are hardly able to jump from one mode to another. We will then refer to them as ‘local’ samplers. Note that they are also generally really slow to converge towards the stationary regime in Bayesian inversion context.

Conversely, the IMH does not need any tuning. It will explore largely the surface of the posterior distribution and we will refer to it as a ‘global’ sampler. Nevertheless, in practical applications, unless q is the posterior distribution, the transitions will obviously almost always be rejected.

Finally, we can notice here that the chain generated by the adaptive algorithm is no longer homogeneous, but it can be proved (see 12–14 in a more general framework) that it has the correct ergodic properties. The idea of adaptive sampling is to improve the proposal efficiency, making it as close as possible to the posterior density. However, it should be stressed here that the algorithm presented above generally fails in a multi-modal context for a low number of iterations (see, e.g. 7). Regarding the Gibbs sampler, it does not seem to be well adapted to the Bayesian inversion problem: the important number of calls of the forward model limits its relevancy.

Due to the sequential nature of the MCMC algorithm and to tackle multi-modality problems, MCMC practitioners generally use several chains that they run in parallel. By simulating several chains, variability and dependence on the initial value are reduced and it should be easier to control convergence to the stationary distribution by comparing the estimation, using different chains, of quantities of interest. However, good performances of these parallel methods require a degree of a priori knowledge on the distribution of interest π, in order to construct an initial distribution on 𝒳 which takes into account the features of π (modes, shape of high density regions, etc.). This is rarely the case in Bayesian inversion. Moreover, in highly non-linear setups, like in Bayesian inversion, a slow mixing chain will presumably stay in the neighbourhood of the starting point with a high probability (see 6 chapter 12 for a more thorough discussion).

Due to the complexity of the posterior distribution (e.g. multi-modality and/or disconnected support) in Bayesian inversion problems and classical limitations of MH algorithms, other methods than classical MH algorithm should be investigated. Simulated annealing and tempering, which are presented in the following paragraph, consists in studying modified versions of the posterior.

2.4. Simulated annealing and tempering

The simulated annealing algorithm has been introduced by Metropolis et al. 8, then generalized by 15 for optimization problems. It can be applied to both optimization and simulation problems (see 6 and reference therein). The simulated tempering has been introduced independently in 16,17.

The fundamental idea of these algorithms is that a change of scale, named temperature, allows larger moves on the surface of the distribution to explore, compared with classical MCMC methods. Indeed, this change of scale avoids the chain remaining trapped in a local mode.

The name and inspiration of the first one comes from annealing in metallurgy, a technique involving heating and controlled cooling of a material to increase the size of its crystals and reduce their defects. The heat causes the atoms to become unstuck from their initial positions (a local minimum of the internal energy) and wander randomly through states of higher energy; the slow cooling gives them more chances of finding configurations with lower internal energy than the initial one. Conversely the tempering is a brutal cooling followed by controlled reheating of the work piece to a temperature below its lower critical temperature. Precipitation hardening alloys, like many grades of aluminium and super alloys, are tempered to precipitate intermetallic particles which strengthen the metal.

These two methods aim particularly at generating samples from Gibbs distribution.

Definition 2.1

A 𝒳-valued random field X, is a Gibbs field of energy E, if its probability density function (with respect to the Lebesgue measure) is (10) named Gibbs density.

For practical problems, the constant 𝒵 is generally intractable due to the dimension of 𝒳. Note that in a wide variety of inverse problems, the posterior distribution (1) takes the form (10); for instance when both prior and measurement error are assumed Gaussian. Note also that simulated annealing and tempering are not confined to cope with Gibbs distributions. We present here both algorithms in this framework for sake of simplicity. For other kind of target distributions π, the practitioner has to consider flattened versions given by π_T = π^1/T.

2.4.1. Simulated annealing

Given a positive temperature T, a Markov chain X is generated from the following Gibbs density: (11)

The simulated annealing is performed by gradually lowering the temperature T from a high value to near-zero. Close to T = 0 the Gibbs distribution approximates a delta function at the global minimum for E(x) (if it is unique). For simulation purposes, the cooling can be stopped at the value T = 1.

This algorithm can be viewed as a non-homogeneous version of the MH algorithm. Indeed, since T decreases along the algorithm, the kernel of the chain varies with time. Classical theoretical results on Markov chains does not apply for this algorithm. Heuristic rules are generally applied to ensure the validity of simulated annealing: the starting temperature must be high enough and its decrease slow enough. A convergence result exists, for optimization purpose, with the condition that T decreases as 1/log(n). In practice, a geometrically decreasing sequence is generally used.

2.4.2. Simulated tempering

The principle of simulated tempering is linked to the simulated annealing one in the sense that we will again consider Gibbs distributions scaled by a temperature parameter T. However, this algorithm aims at sampling from a Gibbs distribution π rather than minimizing the energy of the system. We consider here a finite sequence of temperatures and the associated Gibbs distributions. In this algorithm, we authorize the chain to change temperature level according to a given probability. This will allow the chain to go back to higher temperatures, escaping eventual local modes of the target distribution, that results in better mixing.

We first define an increasing sequence of temperatures 1 = T₀ < ··· < T_K, with its associated Gibbs densities , an auxiliary {0, …, K}-valued variable M and the joint distribution (12) We also define the probabilities p_U and p_D of moving ‘up’ from m to m + 1, and ‘down’ from m to m − 1, with only T changing, the chain being at temperature T_m and the probability of choosing a fixed level move (1 − p_U − p_D).

The principle is to simulate a 𝒳 × {0, …, K}-valued chain (X_n, M_n). Denoting, respectively, q_i→i+1(X_n+1|X_n = x_n) and q_i+1→i(X_n+1|X_n = x_n) the probabilities of transition proposition towards the superior and the inferior temperature level, the acceptance probability of a transition from T_i to T_i+1 is proportional to: (13) To maintain the detailed balance condition, it is then necessary that ρ_i+1→i(x_n+1, x_n) = 1/ρ_i→i+1(x_n, x_n+1) and to choose the proposition distributions q_i→i+1(X_n+1|X_n = x_n) and q_i+1→i(X_n+1|X_n = x_n) accordingly. Still, it is important to notice that (13) depends on the normalization constants of π_i+1 and π_i. We can bypass this difficulty by designing an equal number of moves from m to m + 1 and from m + 1 to m and by accepting the entire sequence as a single proposal, thus cancelling the normalizing constants in the acceptance probability, as described, for example, in 18.

2.4.3. Comments

Attempts to improve mixing properties of the chain by simulated annealing fail generally because of the monotonous decrease in temperature; if the chain gets in a local mode, it may be impossible to escape it if the temperature is already too low.

Concerning the simulated tempering, the potential gain in a better exploration of the support of the target distribution, so as to say, a better mixing does not seem to compensate for the increased amount of forward operator evaluations for inverse problems (2K bigger, for the scheme presented above). However, the presentation of this method is a good introduction to the interacting Markov chains algorithms discussed in the following section.

3. Parallel interacting Markov chains

The principle of making Markov chains interact first appears in 19 under the name parallel tempering (PT). It has mostly been applied in physico-chemical simulations, see 20 and references therein. It is known in the literature under different names such as: exchange Monte Carlo, Metropolis coupled-chain, see 21 for a review. The principle of PT is to simulate a number (K + 1) of replica of the system of interest by MCMC, each at a different temperature, in the sense of the simulated annealing, and to allow the chains to exchange information, swapping their current state. The high temperature systems are generally able to sample large volumes of state space, whereas low temperature systems, whilst having precise sampling in a local region of state space, may become trapped in local energy minima during the timescale of a typical computer simulation. PT achieves good sampling by allowing the systems at different temperatures to exchange their state. Thus, the inclusion of higher temperature systems ensures that the lower temperature systems can access a representative set of low-temperature regions of state space.

Simulation of (K + 1) replicas, rather than one, requires on the order of (K + 1) times more computational effort. This extra expense of PT is one of the reasons for the initially slow adoption of the method. Eventually, it became clear that a PT simulation is more than (K + 1) times more efficient than a standard, single-temperature Monte Carlo simulation. This increased efficiency derives from allowing the lower temperature systems to sample regions of state space that they would not have been able to access, even if regular sampling had been conducted for a single-temperature simulation that was (K + 1) times as long. It is also worth noticing that PT can make efficient use of large CPU clusters, where different replicas can be run in parallel, unlike classical MCMC sampling that are sequential methods. An additional benefit of the PT method is the generation of results for a range of temperatures, which may also be of interest to the investigator. It is now widely appreciated that PT is a useful and powerful computational method.

More recently, some researchers in the statistical community focussed attention on PT and more generally on interacting Markov chains. They proposed a general theoretical framework and new algorithms in order to improve the exchange information step addressed above. Two main algorithms draw our attention: the equi-energy sampler (EES) of 22 and the population importance-resampling (PIR) MCMC sampler of 23, which allows us to go back in the history of the chain. More precisely, these two last algorithms are based on self interacting approximations of non-linear Markov kernels, defined by Andrieu et al. 23. We now describe these methods in the Bayesian inversion context.

3.1. Description of the algorithms

We first recall that our aim is to simulate realizations from the posterior distribution (1). We assume that the posterior distribution π(X) = f(X|d) takes the form of a Gibbs distribution, that is: (14) where E(X) is the energy of the system at the state X. We first define the family {π^(l), l = 0, …, K } of distributions we want to simulate from, such that (15) where , where T_l is the temperature at which the system under study is considered. The T_l satisfy: T₀ = 1 < T₁ < ··· < T_K < +∞, so that π⁽⁰⁾ = π. These distributions are thus a family of tempered versions of ℙ(X|d). To go back to the analogy with the metallurgy, these distributions represent the states of the metal at each considered temperature. At high temperatures, the system can access to high energy states, whereas at low ones, it will attain lower energy, i.e. more stable states. We will also talk of tempered energies to denote the E_l. The parallel algorithms aim to simulate from (16) whilst allowing exchanges between states at different temperatures. Flattened versions of π⁽⁰⁾ : π⁽¹⁾, …, π^(K) are easier to simulate. Thus they can provide information on π⁽⁰⁾. Particularly, the system at T₀ can exhibit a wide range of disconnected meta-stable states (i.e. the different modes of the posterior) and typically, a single Markov chain is not able to visit all of them in the time of the simulation. So, exchanging with states generated at higher temperature allows to explore better support of the posterior.

Different strategies can be adopted to exchange information between chains at adjacent temperatures. For l = 0, …, K − 1, we define the important function (17) which is the unnormalized ratio of the distributions π^(l) and π^(l+1) at a given state x.

From now on, we denote by x = (x⁽⁰⁾, …, x^(K)) ∈ 𝒳^K+1 the current state of the Markov chain that aims at simulating from Π, defined in (16). The method can be formalized by defining the following kernel P_n at time n, given all the previous states x_0:n−1 = (x₀, …, x_n−1) and for A₀ × ··· × A_K ∈ ℬ(𝒳^K+1) (18) where we simulate from π^(K), the chain at the highest temperature T_K, using the classical MH kernel P^(K)(·, ·), whereas at the other temperatures, for , x^(l) ∈ 𝒳 and A ∈ ℬ(𝒳), we will use the heterogeneous Markov kernel: (19) where (20) and in the three algorithms considered here T^(l) will take the following form: (21)

In other words, Equation (19) states that at time step n, temperature T_l, with probability θ, a classical MH move will be performed according to the Markov kernel P^(l)(x^(l), A). Otherwise, with probability (1 − θ), an exchange move will be proposed. It consists in choosing a state y among , the past states of the chain at temperature T_l+1, from the empirical distribution (20). This move is then accepted or rejected according to T^(l) (21). Precisely, going back to (17), it is accepted with probability that is, if the energy of the proposed state y is lower than that of x^(l), the exchange will be systematically accepted.

The empirical distribution can be viewed as an important sampling estimate of π^(l) with the instrumental law π^(l+1) constructed from the past states of the chain at temperature T_l+1. Then, an exchange amounts to simulate directly from an approximate form of π^(l). Note that this will regenerate the chain and hence reduce the autocorrelation along time.

The three algorithms (PT, EES and PIR), considered in this article can be written in this framework and differ only in the formulation of the weights . For some (y, z) ∈ 𝒳², we have

1.	for the PT algorithm it is only possible to go to the current state of the chain at the adjacent higher temperature,
2.	for the EES algorithm, given a sequence of energy levels E0 < E1 < ··· < EK < EK+1 = ∞ defining a partition : of energy rings: 𝒳l = {x ∈ 𝒳 : El < E(x) < El+1} and the function I(x) = l if x ∈ 𝒳l, then the ωn,i takes the following form: that is, the new state of the chain at temperature Tl will be taken uniformly among the states of the chain at temperature Tl+1 that are in the same energy ring as the current state,
3.	for the PIR algorithm, the weights ωn,i take the following form: that is, we obtain the new state by resampling from with the weights ω.

The main idea behind the last two algorithms is that the kernel defined in (19) will converge towards the following limiting kernel: (22) where R^(l) is a MH kernel, whose proposal distribution is given by:

•	for the EES,
•	for the PIR algorithm.

Obviously the convergence towards R^(l) will not be achieved in the time of the simulation, but its approximation at time n will help to sample from the posterior, particularly to span a larger part of the state space.

Finally, it is worth noting that for all three algorithms, we can use the entire sample generated, reweighting the states according to the temperature by the following important weights: (23) in order to compute estimates of I_h = E_π0[h(X)], for some h. Hence, the estimate , after N iteration of the algorithm will take the following form: (24) It has been shown numerically in 22 that using the reweighted entire sample will provide better estimates than using only . Ergodic properties of the whole chain X ∈ 𝒳^K+1 and asymptotic results (law of large number, central limit theorem) regarding (24) follow directly from the properties of each chain used (22,23).

Concerning the choice of the parameters, some heuristic rules exist and are discussed in, for example, 21 for the PT algorithm and in 22 for the EES. Unfortunately, this kind of information does not exist yet in the literature for the PIR. The choice depends mainly on the problem addressed. We give below a few methods for tuning the parameters.

3.2. Tuning the parameters

As the algorithms proposed here are fairly new, we think that some comments from our experience can be useful for future practitioners. These guidelines are purely empirical, based on numerical experiments and our own reflection. We will focus on four different points for the EES and the PIR algorithms:

1.	the kernel to choose, as a function of the temperature,
2.	the sequence of temperature to choose,
3.	the number of chains,
4.	the probability of proposing exchange between chains.

As already claimed, the idea of applying these methods is to improve the mixing of the chain. Then we have to choose kernels that will make this assumption effective. At the highest temperature, large moves tend to be accepted, even though the energy level reached is not as low as the one finally aimed at. Thus, it is of great interest to use a fast mixing kernel that cannot be used at lower energy levels because its transition would be rejected. We then recommend to use a ‘global’ sampler like the independent sampler presented in Section 2.2. However, the highest temperature has to be chosen so that the transition acceptance rate is high enough. Conversely, at low temperatures, it is of interest to have a kernel with good local properties, like the Langevin sampler or a random walk with small steps, that will explore the posterior around the currently identified mode. The point is then to design the kernels between the highest and the lowest temperature levels. The difficulty is to choose kernels that progressively worsen their global properties, while increasing local properties, when descending the temperature ladder. We mean progressively in the sense that the exchange proposal acceptation rate has to stay at a satisfactory level between each chain. In this regard, the kernels proposed in 24 should be useful. In high-dimensional problems, the number of components affected at each transition should vary according to the temperature, modifying more components at high levels than at lower ones, see the application in Section 4.

The sequence of temperatures has to be chosen so as to obtain a satisfactory exchange acceptation rate. In the literature about PT (e.g 20,21), most authors propose to distribute the temperature geometrically. In our applications, we followed this advice and it appeared to work well. The problem is then to choose the highest temperature T_K and the number K, the lowest temperature being always 1. T_K has to be chosen according to the problem considered. Practically, a preliminary study of the energy has to be conducted. This study consists in the computations the energies for an i.i.d. sample (x₁, …, x_n) generated from the prior and calculating its mean . More precisely, assuming that the prior distribution on X is given by g(X) and that the measurement error is Gaussian with identity covariance, F denoting the forward model, the posterior will take the following form: (25) Considering that the realizations X from the posterior show no error, that is F(X) = d, the first term in the expression above vanishes and the energy of the system conditioned by d should be around 𝔼[−log(g(X))], where 𝔼 stands for the mathematical expectation, if the prior has been chosen correctly. The idea is then to choose the highest temperature T_K so as to have . Note that this rule works also when the measurement error is not Gaussian; it needs, however, to be centred. This choice will ensure a satisfactory transition acceptance rate when using the independent sampler affecting all the components at the highest level.

These considerations about kernels and temperatures are closely related to the number K of chains you use. Particularly, it is important not to employ too big a number. Indeed, using more chains will slow the input of information from the highest temperature level to the lowest, the one of interest. Conversely, the number of chains has to be large enough to allow them to exchange information at a good rate. The temperature ladder is then constructed distributing the temperatures geometrically between T_K and T₀ = 1. If the number of chains is sufficient, it allows generally a good overlapping of the histograms of the tempered energies, inducing the occurrence of exchanges. The number of temperatures to use should then be the minimum number that ensures a good overlapping of the histograms of the tempered energies.

Regarding the proposal rate of information exchange, again there is a balance to achieve between high and low rates. A high rate will encourage information exchange, but will slow local exploration. Conversely, a low rate will hamper the process of exchanging information. This depends highly on the dimension of the problem: local exploration is obviously slower in high dimensional spaces. It should generally be between 0.05 and 0.3.

As a conclusion, we can say that on each of the four points addressed here, there is a balance to strike. The idea is to tune the different parameters in order to allow efficient information exchange, while allowing good local exploration at low temperatures and fast mixing at high ones. It may depend strongly on the problem to solve. However, as explained above, a preliminary study of the energies of an i.i.d. sample generated from the posterior should allow the parameters to be tuned satisfactorily. Like MCMC methods, every applied use of these methods requires instinct and understanding both about the underlying model and about the Markov chains being used.

3.3. PT, EES or PIR?

Among the three algorithms proposed here, we claim that the PIR outperforms the two others for Bayesian inversion problems. It is clear that the PT has weaker properties than the two others because it does not account for the history of the chains. Comparing the EES and the PIR, we think the latter is the most suited for our problem. Indeed, considering that the lower the temperature, the slower the chain will enter the stationary regime, we can remark that the PIR does not need the chains to be in stationary regime before to allow exchanges, contrarily to the EES algorithm. Indeed, in the EES, the exchange proposal is made in the same energy ring as the current state. Then, if the chain of interest (i.e. at T₀) has not reached the stationary regime and is still at high energy levels, the exchange proposal will be in the same energy ring as the current state. Therefore, it will not help to attain stationary regime. Conversely, the PIR proposes exchange proposals according to an important sampling step, constructed on the states generated at the higher adjacent temperature. The proposals are then more likely at low energy levels and help the chain to enter the stationary regime more quickly.

4. Application to reservoir engineering

4.1. Introduction

In the oil industry and subsurface hydrology, geostatistical models 25 are often used to represent the spatial distribution of different lithofacies in the reservoir. Two main model families exist: multiple point 26 and truncated Gaussian models 27. We focus here on the latter.

Conditioning the spatial distribution of different lithofacies in the reservoir to production data, such as cumulative oil production water cut, is a highly challenging task in reservoir modelling. It consists in solving an ill-posed inverse problem: given a prior knowledge on the random field governing the lithofacies spatial distribution in the reservoir, typically a geostatistical model, we aim at finding multiple realizations of this model that will exhibit the same dynamical behaviour of the true reservoir. In other words, we want to sample from the posterior distribution defined in the Bayesian inversion framework. This will improve our knowledge of the reservoir and indicate to us what the best exploitation strategy should be, where to dig new wells, in function of all the information gathered. The dynamical behaviour of a given realization is computed by a fluid-flow simulator F.

4.2. The case

We consider a case where the prior on the lithofacies distribution is a 2-dimensional thresholded Gaussian model (see, e.g. 25), with the following characteristics:

•	its size is 2500 × 2500 m2,
•	it is discretized on a regular grid of N = 50 × 50 blocks,
•	it is 10 m thick,
•	the underlying Gaussian random field X has an isotropic spherical covariance structure with a value equal to 600 m (a quarter the field edge size),
•	it is composed of two lithofacies: A (50% with permeability 500 md) and B (50% with permeability 10 md),
•	we put two wells in this field: an injector at grid node (3, 3) and a producer at (48, 48),
•	the porosity is assumed constant at 0.25.

Practically, X is a Gaussian random field with mean zero and spherical covariance whose range a is a quarter the edge of the field 25. The lithofacies field is constructed thresholding X When T(X) = 1, the corresponding cells will be facies A, otherwise B, with its associated permeability value.

The field is assumed to be saturated in oil at time zero. The fluid flow is simulated with 3DSL^© 28, a streamline fluid flow simulator, during 5000 days with an injection rate at 5000 m³/day and a pressure of 200 bars at the producer.

Given a reference realization of the field X* and water cut D* computed on 2000 days, we attempt to condition the geostatistical model X to D* (the water cut being the proportion of water in the oil produced at each time step). According to the methodology introduced in 7,29,30, we choose to use a truncated Karhunen–Loéve 31 expansion with M = 100 components to represent the field. Hence, this approximation reduces the dimension of the inference problem from 2500 to 100, whereas the fluid flow results remain slightly unchanged. 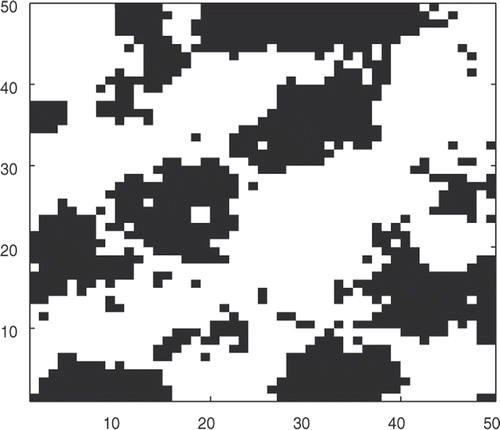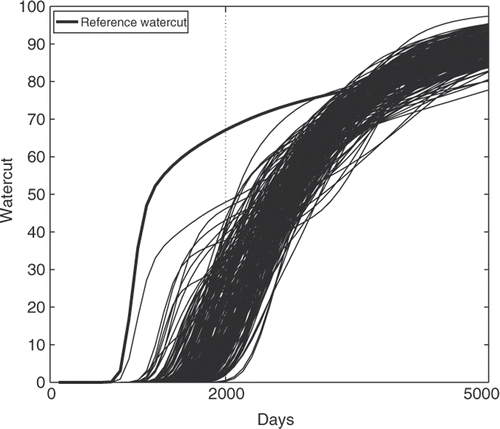The posterior distribution takes the following form: (26) where φ_i(x) and λ_i are, respectively, the eigenfunctions and eigenvalues of Γ_(M). Here, D* and F(X^(M)) are both functions of time. The covariance of the measurement error on the water cut is assumed to be the identity matrix. We represent the reference realization of the field considered here in Figure 1. Figure 2 presents the reference water cut curve together with a sample of curves computed for a sample of 200 independent realizations of the prior. This sample is used to tune the parameters of the algorithm as explained in Section 3.2.

Figure 1. Reference lithofacies map.

Figure 2. Water cut curves of an i.i.d. sample and reference.

4.3. Choice of the parameters of the PIR algorithm

We can see in Figure 1 that there is an important portion of highly permeable (500 md) facies (in white) in the diagonal axis linking the two wells. Figure 2 shows its particular water cut profile: after the early water breakthrough (time when the water cut becomes strictly positive), the water cut increases very quickly, then slows down. This profile is very different from that of the curves of 200 independent realizations of X. Indeed, the minimum energy calculated for this sample is about 3000, with an average around 20,000, whereas we expect the energies to be around 50 for the matched sample (Section 3.2). That proves how challenging our problem is. In order to solve it, that is to sample from (26), we implement the PIR algorithm and a classical component-wise independent MH algorithm, that we will call the single chain (SC) algorithm. The choice of the different parameters, set after some experiments, of the PIR algorithm is inspired by practical considerations given in Section 3.2.

We use five different temperatures, distributed geometrically between T₀ = 1 and T₄ = 400. A geometric distribution of the temperature is then chosen between the two extremal ones. Namely, we take for l = 1, 2, 3. Hence, we use the following temperature ladder: Thus, we simulate the five Markov chains (X^(l)) at the temperature T^l. At T₀, T₁, T₂, we simulate from a symmetric increments random walk MH algorithm with a step variance , affecting, respectively, 5, 20 and 50 components. At T₃, we simulate from an independent sampler affecting 80 components. At T₄, we simulate from a global independent sampler. In other words, proportionally to the temperature, we propose larger moves, using global samplers at the two highest temperatures. Modifying less components at low temperature results in better acceptance rates in our high-dimensional space (M = 100) and allows local exploration of the posterior. Moreover, the moves at the highest temperatures affect more components, thus improve the mixing of these chains and feed the chains (X⁽⁰⁾), (X⁽¹⁾), (X⁽²⁾) with states that they could not have attained without the exchange steps. After a few experiments, we allowed the chains to exchange information according to the PIR scheme just after the first iteration with a probability of 0.05, to ensure local exploration between exchange steps.

4.4. Results

We ran both algorithms for 10,000 iterations. The PIR algorithm took 50 h to run on a desktop computer with a single processor AMD Opteron 146 2.0 GHz and the SC algorithm took about 10 h. Note that having implemented the PIR algorithm on a parallel computer architecture, it would have taken the same time as the SC.

In Figures 3(a) and 3(b), we present, respectively, the energy of the states of the five chains used in the PIR algorithm, and the energy of the states generated by the SC.

Figure 3. Energy of the states, as a function of the number of iterations: (a) five chains by PIR and (b) SC.

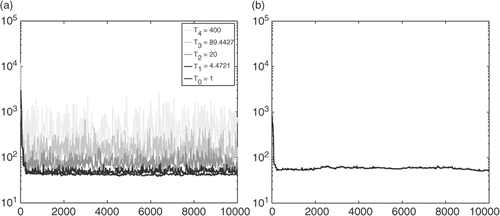
Figure 3(a) shows the energy of the states of the five chains, as a function of the number of iterations. For the lower curve, corresponding to T₀, we observe a stabilization after about 200 iterations, around levels of energy corresponding to the expected order of magnitude of the posterior mean energy. Indeed, allowing exchanges since the beginning of the chain accelerates its convergence. As all the other chains show a stabilized profile of energy after this number of iterations, we consider it as the end of the burn-in period, namely each chain is assumed in a stationary regime beyond this number of iterations. Moreover, we can see that each couple of chains at adjacent temperatures show overlapping energy profiles, allowing the exchanges between the two chains. Indeed, the empirical exchange acceptance rate has been found between 0.6 and 0.8 for each couple of adjacent chains.

Figure 3(b) shows that the SC algorithm exhibits a rather fast convergence towards the stationary regime, attaining energy levels around 50 in about 250 iterations. This amazingly fast convergence is probably due to the starting state generated. It has an energy below 1000, much lower than those observed in our preliminary sample.

Figure 4(a) and (b), shows some statistics computed from the samples generated, respectively, by the PIR algorithm and by the SC algorithm, namely, the median and the 95% percentile confidence interval of the water cut curves generated together with the reference water cut.

Figure 4. Median, 95% percentile confidence interval and reference water cut: (a) PIR algorithm, and (b) SC.

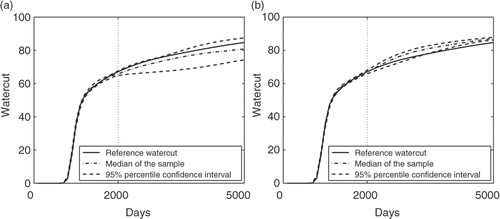
In Figure 4(a), we can see that for the matched period (up to 2000 days), the median of the sample water cut perfectly matches the reference. Moreover, the 95% confidence interval is extremely thin around the reference water cut until 2000 days. Then it widens for the next 3000 days. In addition, the reference water cut stays in the 95% confidence interval and is quite close to the median. This validates our sample for prediction purposes.

Conversely, in Figure 4(b), although the reference water cut is also correctly matched by the sample generated by the SC algorithm, its prediction abilities are rather weak with respect to the PIR algorithm: the confidence interval generated is still thin beyond 2000 days and does not include the reference water cut. This is due to the only local exploration performed by this algorithm.

Figure 5 shows seven realizations by the PIR and one by SC. First, the aspect of the realizations is far smoother than the reference. This is due to the approximation by a truncated Karhunen–Loéve expansion with only M = 100 components. Second, the realizations generated by PIR (a–g) are clearly different from each other (we did not reproduce here the whole variety of maps generated). This illustrates the good exploration of the posterior (26) carried out by the PIR, due to the improved mixing properties with respect to classical single MCMC. Finally, all realizations generated by the SC are similar between each other (Figure 5(h)). It has only performed a local exploration. Note that all the maps generated by both algorithms reproduce a link of highly permeable facies between the two wells.

Figure 5. Seven realizations from the posterior generated by the PIR (a–g). and one generated by the SC (h).

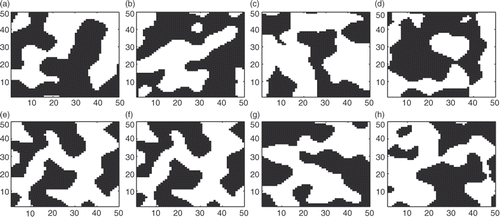
Besides, it is worth noting that the PIR exhibits a global empirical acceptance rate of about 0.4, whereas the SC shows a empirical acceptance rate around 0.1. In other words, comparatively, we throw away twice as many fluid-flow simulations with the SC than with the PIR.

To sum up the results on this synthetic test case, the PIR has shown improved mixing properties compared with the SC. It has provided a sample with good predictive properties, representative of different modes of the posterior.

5. Conclusion

In this work, we have first described the main principles of classical MCMC methods and related techniques simulated annealing and simulated tempering. We have then proposed an innovative application of a recent stochastic simulation method, based on parallel interacting Markov chains. We also provided some general guidelines for the tuning of the parameters of these algorithms. Finally, an application on a synthetic case of reservoir characterization has been performed. The numerical results show clearly that the PIR algorithm outperforms the single Markov chain for sampling the posterior. The sampling carried out by PIR explores better the posterior, therefore the sample produced has a better capacity of prediction. Moreover, this method is well suited for parallel computing, thus comparable with the classical MCMC in terms of computation costs.

The parallel interacting methods presented here, like other MCMC methods, aim at generating samples approximately distributed from a given distribution, without directly simulating from it. Although presented in the Bayesian inversion context, these methods can be applied in a wider range of applications, for instance simulation problems in statistical mechanics (see the literature about PT and references therein, e.g. 20,21). Moreover, parallel interacting Markov chains algorithms can be easily combined with surrogate or approximate models approach, where a faster version of the forward model is used (see e.g. 32–34).

Further improvements can be made on the parameterization of the parallel algorithm. It should be of great interest to imagine an automatic tuning of the kernels parameters, namely, the number of components affected at each iteration and the variance step used in random walks, according to the temperature.

Finally, the problem of integrating new data in an existing model can be performed in the following way: we could use either the above method with the kernel given by the final estimation of (22) or an important sampling resampling scheme 6. The latter consists in proposing a realization with the weights given by (23), then reweighting them according to the adequation of new data.