Abstract
In the present article, the inverse problem concerning the identification of suitable sensitivities for inertia measurement sensors, part of an inertial navigation system, is discussed. For a precise tuning of the navigation system, it is assumed that the sensitivities could modify their effective values as the consequence of instantaneous movements and environmental conditions. The goal is to set up a tool that is able to foresee any possible sensitivity scattering. The key point is to find a strategy to teach a neural network (NN) to be able to correct measurements when auxiliary global positioning systems (GPS) are not properly working. In this article the strategy is presented and discussed and several tests show some examples in which the procedure was successful or not. However, for all unsuccessful cases, it is possible to recognize the malfunctioning prior to complete the identification; therefore, data to discard in the NN training are easily identified. The final NN application is not discussed within this article because it is non-essential for the present aim that is the definition of optimal NN output parameters.
1. Introduction
Navigation systems are experiencing an enormous increase in diffusion, due to the commercialisation of very low-cost global positioning systems (GPS) receivers. However, GPS, exploiting information sent by satellites orbiting the earth, present some important restrictions. The visibility of satellites is not always guaranteed to vehicles in all situations (tunnels, roads surrounded by trees, high buildings all around, etc.), so that satellite data are not available at all times. As it is well-known, the overall precision for a non-stationary GPS receiver is above 10 m Citation1. This number represents a lack of precision for small and short time displacements, but it results in a very high accuracy when large distances are considered.
Inertia measurement systems (IMS), in strapdown platforms Citation2, are substantially based on acceleration and angular velocity measurements. In contrast with GPS, the IMS are characterized by fine accuracy only within a short measurement time. They suffer the so-called random walk that is generated by accumulated errors during integration over time. Therefore, for short-distance measurements, or for a small time, IMS demonstrate a finer precision if compared to GPS systems.
Furthermore, in any situation when GPS data are degraded at such a level to be useless, IMS are the most important navigation tool. The first systems were based on gimballed mounting of accelerometers, thus keeping the probe at a fixed orientation (towards any inertial reference system) while moving. Today Micro Electro Mechanical Systems offers the opportunity to introduce very efficient rotational-speed gauges, so that strapdown systems are the most widely diffused. Efficient, but expensive systems are used in military and aeronautical applications; these systems are based on high-class sensors, but the extension to other civil and worldwide applications would be possible only if low cost sensors could be used.
The main expectation is therefore an integrated use of the two systems – GPS and IMS – in order to gain the best advantages from both of them. It is, however, necessary to increase the overall precision of the IMS that cannot be considered reliable when low-cost gauges are used. As a matter of fact, low-cost sensors modify their responses according to: environmental condition, coupling of excitations in different orientations, effective movement experienced, power supply voltage, local pressure, temperature and humidity, etc.
The first proposed integrated systems were based on Kalman filtering Citation3 that is a tool able to deal with signals suffering noise. Even if good outcomes have been claimed by authors, the techniques proposed do not solve the problem in general applications Citation4,Citation5. The scattering of low-cost sensors cannot be simply modelled as a white noise; therefore, Kalman filtering is not indicated as the only main road to follow. Kalman filtering is able to study the response of linear systems, but some significant improvements have been proposed to extend its applicability Citation5,Citation6. Artificial intelligent systems (AIS) have been used for a decade to foresee the IMS errors by many authors. The results are encouraging, but the AIS results depend strongly on the likeness that happens between the phases of training and predicting phases Citation7,Citation8.
The attitude determination of a rigid body Citation9 leads to a strongly non-linear solution problem; therefore, any error on measurements is heightened by this complexity. The question of an optimal tool to integrate the satellite and the IMS was faced in Citation10, the authors clearly showed that this aspect is a key factor for navigation purposes. Assuming that the gauge's responses are the only cause of errors in the measurements, it is, however, not easy to make explicit the correlation between the inaccuracies of the sensors and the errors in the resulting position Citation11,Citation12. Rotations introduce a strongly non-linear behaviour to the dynamic study of a system, so that it is hard to find an explicit link between the individual errors of the sensors and the corrections of the six variables giving positioning and orientation.
The neural networks (NN) are an excellent tool to provide evidence of the correlation between input and output variables even if non-linear relations occur. However, the focus of this article is devoted to presenting the variables in such a form that the training phase is enormously simplified. The basic idea is to relate the output errors to the individual response of the six main sensors through the solution of the resulting inverse problem. Under these conditions, the sensitivities of each sensor are the unknowns; the correlations between each unknown and the history experienced are searched by the NN. The method uses a measurement platform that is illustrated in Citation13 and a NN approach that is described in Citation14.
This article does not report on NN response, but it is mainly interested in the solution of the inverse problem. This management of the results, according to the author, allows the NN to be trained in an optimal way, avoiding possible over fitting of the network, as well as its inability to connect the errors to measured physical quantities. In synthesis, the assumption is that the more the correction parameters are directly connected to the physical source of errors, the more the network will be capable of a general (that is to say not specialized) application.
2. Use of neural network in the navigation system
The NN approach divides the problem into training and predictive phases. We ideally consider the two phases as being separate, but it is important to consider that the training can be performed through the whole life of the system, so that shifts of the sensor characteristics during working could be faced.
In the case examined, GPS results are the reference ones. As previously mentioned, this is acceptable only if the measurements are taken under some conditions: optimal visibility of satellites; high number of satellites simultaneously in touch and optimal geometrical positioning of satellites; a period of stationary dynamic conditions such as those given by a straight road (given by stationary values of the gyroscopes); non-aligned attitude between two consecutive GPS positioning; data considering a reasonable distance. Therefore, a first point is the identification of an optimal reference group of GPS data. Couples of GPS data give the attitude and positioning of the initial point and the final point of a path.
Note that all the above conditions do not restrict the problem too much, since it is reasonable to assume that training is performed only if reliable data are managed. Thus training can be extracted and handled as partitions of a long acquisition time, with no need to manage only consecutive data.
When an optimal path is selected, we have the initial and final positions of each trip. By making use of this information, the search is performed on sensor effective sensitivities (the output).
After performing the training phase, the prediction consists in the real time correction of the sensitivities of the inertia sensors used during time integration. Of course, the prediction should be reliable when a GPS outage occurs.
The problem is first presented in the two-dimensional case for which a solution in closed form is provided, and then it is extended to the three-dimensional case for which an iterative solution is obtained.
2.1. The two-dimensional case
In the two-dimensional case, the unknowns consist of six calibration correction factors (αL, αT, βL, βT, γL, δL, L-longitudinal, T-transverse, N-normal) in a three degrees-of-freedoms problem (x,y,θ), as shown in . Six conditions must be satisfied.
Figure 1. Reference frames for the 2D (a) and 3D (b) problems.
For simplicity, the longitudinal direction at time zero lies on the x-axis.
In the two-dimensional case let us assume that the sensitivity errors are dependent upon constants and linear time-increasing values. Using subscript v for the true values of accelerations and angular velocities, they are linked to the measured ones through unknown correction factors (acting on sensor sensitivities)
(1)
(2)
(3)
It is assumed that position, angular speed and orientation are perfectly known at reference times 0 and tf. First, the jaw angle θ is defined through the integration of Equation (3)
(4)
Considering the first and the last terms in Equation (4), together with Equation (3), the solution for the unknowns γN and δN – being independent upon integration – is straightforward and consists in the solving of a two-variable problem. The only point on which to focus attention is to consider the number of eventual loops experienced during the trip. This information is embedded in the integrals of Equation (5). Of course, whenever the total error is higher than 2π, the solution gives erroneous values for the unknowns; but this is only possible if very degraded acquisition data are collected. An undetermined problem also occurs when the initial and the final orientations are the same and the angular speed is also unchanged (an homogeneous problem results). Dropping the subscript N on ω Equations (4) and (3) yield
(5)
The subsequent treatment of accelerations requires previous solution results together with a continuous reference change from L-T to x-y systems, as follows:
(6)
Now substituting Equations (1) and (2) in Equation (6), we get the relation between the true values in the fixed frame and the measured ones
(7)
Focussing attention on x-direction only, first and second integrals of (7) give
(8)
(9)
Analogous equations can be written for the y-direction.
Equations (8) and (9), written for both translational degrees of freedom, give a system of four equations with four unknowns. The solution always exists if the vehicle moves away from the original position during time tf, as explained above.
2.2. The three-dimensional case
Hereinafter the linear components of the sensitivity errors have been neglected for the sake of simplicity.
Again, two separate steps can be identified. The first one regards the correction of the attitude of the vehicle at the initial and the final measurement time. In this phase, the solution is restricted to the gyroscopes (here measuring angular velocities) and more precisely to their sensitivities. The second problem starts when optimal orientation towards time is found and the search for acceleration sensitivities that makes the positioning correct begins. It will appear soon that the first problem that regards gyroscope tuning is strongly non-linear, since the final orientation is subjected to all three sensor deficiencies at the same time. During the evolution of the attitude, in the actual reference frame of the sensor box, each instantaneous rotational speed vector projects on all components of the fixed frame. This projection accounts for the whole history within the path. Therefore, the contribution of each gyroscope error to the global error of the final attitude is hard to calculate.
An efficient strategy yields a stepwise procedure that accounts for each single rotation act. This way of proceeding is essential to guide the solution towards the correct one. The accomplishment of the solution is, however, not always guaranteed, but this limitation, as already stated, does not affect the NN training phase. As a matter of fact, when the solution is unavailable – and this fact is clearly evident from the non-convergence of the final attitude to the expected value – its contribution is discarded in the NN training. The subsequent tuning of accelerometers is then performed, it is the second part of the problem: it is again straightforward and gives a unique solution as discussed for the 2D case. In other words, the correct positioning of the vehicle is almost always possible, but the solution has an effective utility if both correct attitude and positioning are attained.
The reference figure is now .
The total number of unknowns is six (αL, αT, αN, γL, γT, γN) and the system is described on a six degrees of freedom base (x, y, z, θx. θy, θz) through the following measurements:
(10)
(11)
(12)
(13)
(14)
(15)
For the first step, attitude correction, it is not possible to write integral solutions in an analytical form. As a matter of fact, the error introduced by a sensor to the attitude values – evaluated in the fixed frame – depends on all previous movements in a non-linear way. This is due to reference transformations, similar to (6), introducing rotational matrices. However, one can memorize the overall influence of each motion act in the fixed frame and use this information to build a weight matrix. This matrix is then used to perform a conditioning of the solution itself. The weight matrix is hereinafter called Cbt. To clarify the matrix assembling, let us follow the transformation of a single motion act from the moving to the fixed frame. The actual orientation of the moving frame is defined through a direction cosine matrix CD.
For a time increment dt, the following infinitesimal rotations occur:
(16)
with an overall angle of rotation given by
(17)
In practice, the motion act is given by a rotation around an axis whose versors are given by
(18)
The rotation around the axis causes a rotation of the reference frame given by an exact rotational matrix dCD – where the t variable has been eliminated for clarity:
(19)
This matrix is used to get the new orientation of the moving frame at time t + dt, namely
(20)
At this stage, the contribution given by the local reference rotations to absolute directions x,y,z can be computed – independently on sign – by projecting the three components of axis R in the absolute reference:
(21)
A 3 × 3 dCbt matrix is thus built. Each step is characterised by its dCbt matrix; it is reasonable to sum up the absolute values of these matrices, for the whole measuring time, to get an overall influence of local ω in the absolute frame, namely
(22)
In its general form, this matrix is formed of all non-vanishing terms. As an example, the term 2–3 measures the overall influence that ωT has on final orientation θz.
The final orientation is defined by the matrix given by Equation (20), evaluated at time tf.
We also need a way to compare two different final reference frames. To this end, the inverse operator given in Equation (19) allows the angles formed by the axis of two reference systems, respectively to be found
(23)
(24)
(25)
The computation of the angles σ makes use of noisy measurements (16); therefore, these values are different from the expected values, here called Σ. Optimal values of unknowns γL, γT, γN should minimize the difference between σ and Σ.
The way to solve the correction factors γi turns into an iterative procedure. The values assumed in the right-hand side of Equations (13–15) are continuously updated at each iteration, so that γi tend to be infinitesimal.
Assuming that at each iteration step there is a simple linear relationship between the correction factors γi and Σi − σi, the new correction factors are given by
(26)
The vector loopABS accounts for absolute multiples of π in the integration of the angular speed, due to the periodicity of solutions (24) and (25).
Equation (26) does not take into account the Cbt matrix that shows the non-linear relation between angular errors and correction parameters. A new form for the iterative step is thus proposed
(27)
The use of this form, in the replacement of (26), proved to be very effective for the search of optimal attitude results. It helps start the search on the right path during the converging process. The iteration process ends when a target precision is gained, or if the process is unable to further improve the results.
In any case, checking the distance between σ and Σ enables the opportunity to continue with the second phase, the correction factors for accelerometers. Again the solution is exact, but its usefulness depends only on the precision previously attained in the attitude control. This is to say that it is always possible to find the correction factors of accelerometers that are able to correctly position the vehicle from the origin to its final location.
This second part is briefly explained, also considering the effect of gravity acceleration measured by accelerometers. The direction cosine matrix is
(28)
Remembering definitions (10–12) yields
(29)
Developing, as an example, for x-axis
(30)
(31)
The solving system is formed from three equations and three unknowns. Introducing the gravitational G vector and grouping integrals as follows:
The final system is found as
(32)
As mentioned, the solution is always found, but its physical meaning is connected to a previous good update of the attitude.
3. Discussion of results
As already mentioned in the preceding section, the focal point of the procedure is the correction of the measured angular velocities. Here only simulated tests are discussed; therefore, the effective values of the correction factors to be found (the objective) are known for the purpose of comparison. In this case, the quality of the solution can be checked from two points of view: the reconstructed kinematical variables towards the exact ones, and the distance between the true values of gauge sensitivities and the correction factors introduced for them. First, some examples are presented for the 2D case.
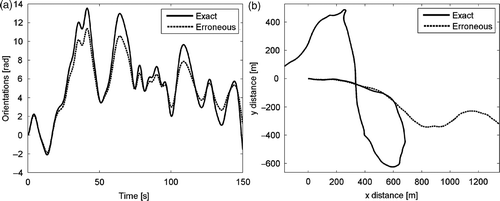
In , the scatter between the exact and erroneous (hereinafter erroneous stands for simulated measurement containing errors) is shown. The results are obtained adding a deterministic error on sensors sensitivity between 30 and 40% of the exact values. Note that orientation and trajectory are completely independent of each other, so that the vehicle is not forced to move tangent to its front end. As expected, although the initial paths are far away, the result is perfect after correction, as is shown in regarding corrected orientation and positioning (the two results are well superimposed).
Figure 2. Orientation error (a) and 2D trail on a map (b) during a 150 s simulation.
The same optimal solutions are found even if the initial error on sensors is amplified 10 times more than before ().
Figure 3. Optimal correction of orientation (a) and positioning (b) during a 150 s simulation.
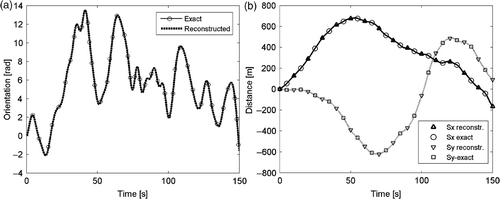
Even if the solution is exact, it is important to note that data used to get the solutions (position, attitude and eventually speed at initial and final time) are subjected to uncertainty. The robustness of the solution can be studied by considering a 2% change on these last reference data; the orientations move slightly, but the change is very evident for the other kinematic quantities, as shown in . According to this preliminary analysis, setting the expected GPS accuracy to 20 m, one should consider the path as long as 1000 m.
Figure 4. 2D trail on a map (a) and displacement components (b) when sensitivity errors are increased 10 times.
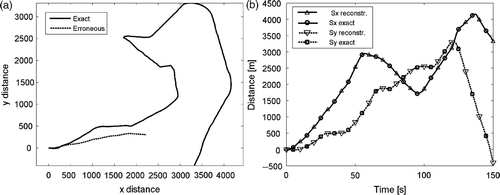
As a general outcome, proven by many other tests, any orientation error considerably amplifies the errors in the resulting trajectories. Therefore, a bad correction of the orientation should induce the analyst to omit the search for correction on accelerometer sensitivities. Also, if one reduces the measured time, the sensitivity towards uncertainty decreases significantly. It is thus possible to perform a trade-off by searching for the optimal time span of a path for the purpose of the correction of the sensors.
Figure 5. Identification on data containing 2% error in final positioning, orientation (a) and velocity correction (b).
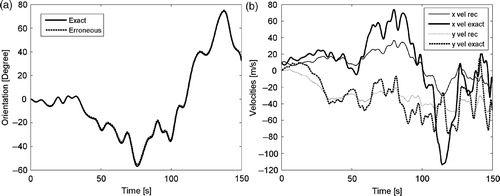
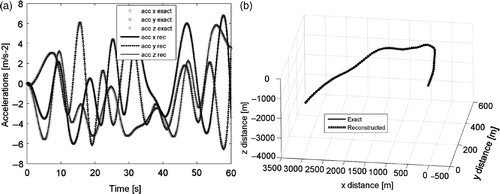
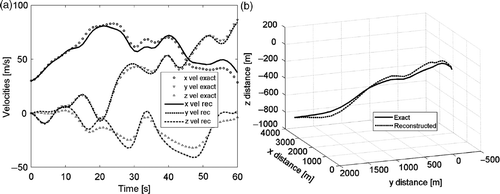
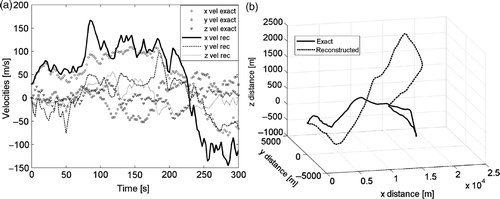
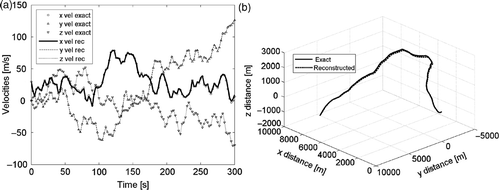
In the 3D examples, the solution is found through an iterative non-linear process. Depending on the whole history, it can happen that the solution is very good, (). But it can also happen that the solution is not excellent, as in the case presented in . It is not simple to have a clear idea whether the non-linear solution has to find a good result or not. However, a consistent error of attitude identification is the main sign of an unacceptable reconstructed path.
Figure 6. Example of optimal reconstruction of acceleration (a) and 3D path (b).
Even if the measurement time increases considerably, up to 6 min in the following examples, it can happen that the solution was good or not. In any case, the NN system only keeps the acceptable results for its training. The training can last as long as it is required until a sufficient amount of data is collected.
Figure 7. Non-optimal velocities (a) and 3D path reconstruction during 60 s measurement (b).
refer to a very bad case, the solution is completely missed. On the other hand, shows a successful case, even if the measurement time is likely to make the path quite complex.
Figure 8. Missed velocity (a) and 3D path reconstruction over a 300 s measurement (b).
Figure 9. Optimal velocity reconstruction (a) and 3D path on a 300 s measurement (b).
reports all the exact and estimated correction parameters presented for the cases shown in Figures .
Table 1. The exact and estimated correction parameters presented in Figure .
At the present stage of analysis, no criterion was found to know in advance if a non-linear solution, solving the inverse problem of measurement sensitivities, should be successful or not. This is not, however, significant for the training procedure. Furthermore, it seems interesting to avoid the use of attitude measurements to get optimal gyroscope sensitivities. It is probably possible to use several contiguous locations to find on-a-whole gyroscopes and accelerometer correction factors. This point addresses even more complex inverse solution processes, not discussed in this article, but it will be the subject of future developments.
4. Conclusions
The solution proposed to identify the effective sensitivities of inertia measurement sensors is able to give optimal results in all two-dimensional tests and most of the three-dimensional ones examined. However, the procedure fails in a certain number of cases, not necessarily in connection with the complexity of the path. Despite this, it is not essential to increase the effort to find solutions for such cases, since it is always possible to easily check the physical suitability of the solution. Future developments regard the chance to omit reference attitudes, but this increases the complexity of the solution.
References
- Grewal, MS, Weill, LR, and Andrews, AP, 2001. Global Positioning Systems, Inertial Navigation, and Integration. New York: John Wiley and Sons Inc; 2001.
- Garg, SC, Morrow, LD, and Mamen, R, 1998. Strapdown navigation technology: A literature survey, J. Guidance Contr. Dyn. 1 (1998), pp. 161–172.
- El-Sheimy, N, An expert knowledge GPS/INS system for mobile mapping and GIS applications. Presented at Proceedings of the 2000 National Technical Meeting of the Satellite Division of the Institute of Navigation. California, USA, 26–28 January, 2000.
- Brown, RG, and Hwang, PYC, 1992. Introduction to Random Signals and Applied Kalman Filtering. New York: John Wiley & Sons Inc; 1992.
- Vanýćek, P, and Omerbasic, M, 1999. Does a navigational algorithm have to use Kalman filter?, Can. Aeronaut. Space Inst. J. 45 (1999), pp. 292–296.
- Faruqi, FA, 2000. Non-linear mathematical model for integrated global positioning/inertial navigation systems, Appl. Math. Comput. 115 (2000), pp. 191–212.
- Noureldina, A, El-Shafiea, A, and Tahab, MR, 2007. Optimizing neuro-fuzzy modules for data fusion of vehicular navigation systems using temporal cross-validation, Eng. Appl. Artificial Intelligence 20 (2007), pp. 49–61.
- Peng, YK, and Golnaraghi, MF, A vector-based gyro-free inertial navigation system by integrating existing accelerometer network in a passenger vehicle. Presented at Proceedings of the Position Location and Navigation Symposium. 2004.
- Larin, VB, 2001. Attitude-determination problems for a rigid body, Int. Appl. Mech. 37 (2001), pp. 722–733.
- Wagnera, JF, and Wieneke, T, 2003. Integrating satellite and inertial navigation – Conventional and new fusion approaches, Contr. Eng. Practice 11 (2003), pp. 543–550.
- Wagner, JF, 2004. Adapting the principle of integrated navigation systems to measuring the motion of rigid multibody systems, Multibody Sys. Dyn. 11 (2004), pp. 87–110.
- Kong, X, 2004. INS algorithm using quaternion model for low cost IMU, Robotics Autonomous Sys. 46 (2004), pp. 221–246.
- Angeloni, F, Locci, A, Marotta, E, and Salvini, P, Applicazione di una Rete Neurale per la correzione di traiettorie. Presented at Proceedings of the XXXVI AIAS Conference. Ischia, September, 2007.
- Angeloni, F, Locci, A, Marotta, E, and Salvini, P, Un sistema di navigazione inerziale per il trasporto terrestre. Presented at Proceedings of the AIMETA Conference. Brescia, September, 2007.