A regularized solution for the inverse conductivity problem using mollifiers

Abstract

In this article, we present a reconstruction method for the inverse conductivity problem suitable for smooth conductivity distributions. The inverse problem is reformulated in terms of a pair of coupled integral equations, one of which is of the first kind which we regularize using mollifier methods. An interesting feature of this method is that the kernel of this integral equation is not given, but can be modified for the choice of mollifier. We are able to obtain conductivity reconstructions rapidly and without relying on accurate a priori information.

Keywords:

• inverse conductivity problem
• electrical impedance tomography
• integral equation methods
• mollifiers
• nonlinear inverse problems
• ill-posed problems

AMS Subject Classifications::

• 31B10
• 45Q05
• 45B05
• 47A52

1. Introduction

The inverse conductivity problem has attracted much attention and one of the main reasons is that although in its basic form the problem is relatively easy to state, it is extremely challenging mathematically. This is because it turns out to be both nonlinear and, above all, extremely ill-posed in the Hadamard sense. A further very positive aspect of the problem is that it has a practical realization which is known as electrical impedance tomography (EIT). This application, which has its own substantial challenges in the fields of biomedical engineering and instrumentation, offers the possibility of a whole range of exciting and extremely useful applications in medical or industrial tomography at a very modest cost.

Substantial progress has been made in determining the class of conductivity distributions that can be recovered from the boundary data 1–5, as well as in designing practical reconstruction algorithms applicable to noisy measurement data. Reconstruction procedures addressing the full nonlinear problem include a wide range of iterative methods based on formulating the inverse problem in the framework of nonlinear optimization. While these techniques are promising for obtaining accurate reconstructed conductivity values, they are often slow to converge and are quite demanding computationally particularly when addressing the three-dimensional problem. These concerns have encouraged the search for reconstruction algorithms which reduce the computational demands. Some use a priori information to reconstruct piecewise constant conductivity distributions e.g. 6–8 while others are based on reformulating the inverse problems in terms of integral equations 9–14. This list is by no means exhaustive and new approaches are constantly being presented 15.

In this article, we describe a reconstruction method suitable for smooth conductivity distributions. It uses a simple transformation to establish a connection between the equations defining the inverse conductivity problem and those used in inverse scattering 16. By combining this process with the concept of mollifiers 17–21 we are able to obtain conductivity reconstructions for arbitrary geometry, extremely rapidly and without relying on accurate a priori information. This is achieved by reformulating the inverse problem in terms of a pair of coupled integral equations, one of which is of the first kind which we solve using mollifier methods. An interesting feature of this method is that the kernel of this integral equation is not given, but can be modified for the choice of mollifier.

The article is organized as follows: Section 2 gives an outline of the basic reconstruction method. In Section 3, we describe the concept of mollifiers and discuss the advantages of this approach. In Section 4, we show how the technique described in Section 2 can be regularized using mollifiers and in Section 5, we discuss the choice of optimal boundary data. Section 6 contains the numerical experiments, which indicate the possibilities and limitations of the combination of these two powerful theoretical tools.

2. The basic approach

Let Ω ⊂ ℝⁿ, n = 2 or 3, be a bounded simply connected domain with boundary ∂Ω ∈ C² and let σ be an isotropic conductivity distribution in Ω, where 0 < c ≤ σ < ∞ and . It is well known that if an electric current is applied on ∂Ω then the induced electric potential Φ satisfies the equation (1)

Using the well-known change of variables we can rewrite Equation (1) in the form (2) where (3) (4) and Φ₀ is an arbitrary constant.

In this work we will assume that from data measurements on the boundary we have a knowledge of both σ and Φ and their normal derivatives on ∂Ω. The inverse conductivity problem is to use this information to identify σ in Ω. Although it might seem that our inverse problem is overdetermined, we do not use all this information but only certain linear combinations. In terms of the new variables, the reconstruction problem becomes that of finding V (and consequently σ) from a knowledge of Ψ and on ∂Ω, which is similar to the data normally used.

Definition 2.1

Suppose λ : Ω → ℝ is bounded. Let ℋ : Ω × Ω → ℝ be a bounded solution of the Schrödinger equation with respect to the second variable, i.e. (5) Let ℱ be the set of functions f : Ω → ℝ which satisfy the Schrödinger equation (6)

Remark 1

Since ℋ(x, ·) ∈ L^∞(Ω) and ℋ(·, y) ∈ H²(Ω), ℋ is a function of Hilbert–Schmidt type.

We can apply Green's second identity 22,23 to the functions Ψ and ℋ defined above, and to Ψ and the free space Green's function for Schrödinger's equation (4), 𝒢₀(x, y), to derive two integral representations of problem (2): (7) (8) where (9) (10) (11)

Remark 2

Note that the above formulation can also be applied to σ ∈ W^2,∞(Ω). The reconstruction algorithm described below needs more care when applied to such weakly constrained conductivities and we will consider this in future work.

This integral equation formulation will allow us to develop a procedure for determining σ that is described in Section 3. It is important to note that since Equation (6) is a Fredholm integral equation of the first kind, it is severely ill-posed and its solution has to be regularized. In this article, we examine the use of mollifiers to achieve this regularization. Finally, it is interesting to note that we have the possibility of choosing a function ℋ(x, y) which is either optimal in some sense or which has other desirable properties, yet to be determined.

3. A mollifier method for impedance tomography

Let us assume that σ, Ψ and are known on ∂Ω and that an appropriate function ℋ has been chosen. The reconstruction of σ in Ω using the formulation described in Section 2 then consists of four steps:

1.	Solve the linear problem AX = ζ (given by Equation (6)) where (12) The reconstructed X(x) will be an approximation to (V(x) − λ(x))Ψ(x), x ∈ Ω.
2.	Compute Ψ(x) for x ∈ Ω using a simple quadrature in Equation (7).
3.	Compute V(x) for x ∈ Ω using Equation (8) (13) Any computational difficulties related to very small or zero values of Ψ(x) in Ω can be avoided by an appropriate choice of the constant Φ0 defined in Equation (3b).
4.	Compute by solving (14) with given boundary values τ(x) and , x ∈ ∂Ω.

Note that this procedure has transformed the nonlinear ill-posed inverse conductivity problem into a linear ill-posed problem (step 1) followed by a nonlinear process (step 3) leading to a unique stable solution of the partial differential Equation (13) (step 4). Note also that once a regularized solution to Equation (6) has been found, the conductivity distribution inside Ω will be uniquely reconstructed by following the remaining steps of the algorithm.

The solution of the ill-posed linear problem in step 1 can be stabilized using any regularization method for integral equations of the first kind. However, mollifier methods offer certain advantages as follows:

i.	Applications in medicine or geophysics will require different resolutions in different regions of Ω. This requirement might depend on the distance of the reconstruction point x from the measurement equipment or allow us to incorporate some a priori knowledge about homogeneous subregions. Locally adapted resolution can be easily incorporated in a mollifier approach.
ii.	The inversion of A is an ill-posed problem and data errors of ζ are amplified in the reconstruction. The mollifier approach overcomes this problem by requiring us to solve an operator equation for every reconstruction point x with an analytically given exact right hand side. This intermediate step can be precomputed with arbitrary precision.
iii.	Once the pointwise reconstruction vectors have been precomputed, the final data-dependent reconstruction step simply requires the computation of one scalar product per reconstruction point.

The mollifier method is a pointwise reconstruction technique 17–20 and is a generalization of the Backus and Gilbert method 24,25. It is based on a Dirac-sequence , such that (15) A standard choice of mollifier is given by (16) and this is the one we use in this article. The parameter γ is called the resolution or the regularization parameter at the point and .

Now assume that a reconstruction point and a desired resolution γ have been chosen. The value of γ may vary for different reconstruction points but we will suppress this dependence to simplify the notation in this article. Instead of reconstructing X itself, we attempt a reconstruction of (17) Since is fixed for the moment, we have (18)

The adjoint operator A* of the operator A defined in (11) is given by

The use of mollifier methods as a regularization technique was introduced in 17. The basic idea is to find, at each reconstruction point , a function satisfying (19) or to compute a minimum norm approximation to by solving (20) We can then easily estimate (21) Consequently, the reconstruction at the point is achieved by simply computing a scalar product of the data ζ with the precomputed . The construction of requires us to solve the ill-posed operator Equation (18). However, this can be precomputed and, more important, the right-hand side of Equation (18) is known exactly.

4. The choice of mollifier

The choice of the mollifier will determine the quality of the reconstruction and its selection should reflect the properties of the operator as well as information about the quality of the data. However, we have another degree of freedom in the reconstruction process described above: the choice of the function ℋ. In other words, the choice of the kernel of the integral operator is at our disposal. This is very different from the situation in standard linear inverse problems and will be the key element for our further investigations.

Let us begin with a discussion of the mollifier , , . Let , where u_γ is the minimizer of Equation (19). This implies that we actually do not reconstruct (22) but rather (23) In order to determine we first need to determine the range of A*. This range depends on the choice of the integral kernel ℋ.

LEMMA 4.1

Range (A*) ⊂ ℱ.

Proof

Consider f ∈ L²(Ω), then it is straightforward to show that ▪

Hence we can aim at best at an effective mollifier , which satisfies the Schrödinger equation (4) in y.

Definition 4.2

We denote by (24) an orthonormal basis for ℱ.

The effective mollifier at point is given by (25) Since the range of a nondegenerate compact operator A* is not closed, we still cannot ensure that (19) can be solved with e_γ replaced by . However, the kernel ℋ of A* is at our disposal and we can easily ensure by choosing (26) with bounded coefficient functions {c_l(x)} satisfying (27) The computation of the reconstruction functional is now achieved using (28) Since h_l ∈ H²(Ω), then by embedding theorems h_l ∈ L^∞(Ω), and the validity of reversal of the summation and integration is guaranteed by the Weierstrass M-test 26. The solvability of gives another restriction on the kernel ℋ. Comparing Equations (24) and (27) we can see that this equation is satisfied for any {c_l} and u_γ provided (29) Let us summarize the previous calculations.

LEMMA 4.3

For a fixed point , let denote a mollifier function, and its projection on ℱ given by Equation (24). Determine and {c_l|l ∈ ℤ} satisfying Equations (26) and (28).

Choosing the kernel ℋ(x, y), x, y ∈ Ω, of A* by leads to a reconstruction functional such that

We can simplify these calculations since for the actual computation we do not need to use the special choices of c_l and u_γ. In order to see this let us be more specific. Recall that we have as data

THEOREM 4.4

For a fixed point , let denote a mollifier function, and its projection on ℱ given by Equation (24). Then the mollified approximation to the solution X of Equation (6) at is given by (30)

Proof

The right-hand side of the integral Equation (6) is given by Hence we have to solve AX = ζ. The reconstruction at is obtained by Inserting the series expansion of ℋ, see (25), and the definition of ζ yields The integral over the variable x gives the value 1 independent of l, see (28). Hence interchanging summation and integration (again justified by the fact that h_l ∈ H² and using the Weierstrass M-test) gives the desired result.▪

Remark 1

It is interesting to note that the calculation of the regularized solution X_γ at a point using Equation (29) involves only an integration over the boundary ∂Ω and not the whole domain Ω. Moreover, the above theorem applies to any equation of the form (6). However, if in addition we assume that (6) is an integral formulation of Equation (2) the result of Theorem 4.4 can be obtained with the use of Green's formula for the functions Ψ(x) and as follows:

5. Choice of currents and voltages

The choice of ℋ allows us to compute the projection of X = (V − λ)Ψ in ℱ from a single set of data measurements, namely (). Hence, in general, we can achieve only a partial reconstruction of V and σ with one set of measurements, but several strategies for combining different measurements have been investigated, see for example 27.

However, there may be special cases where a single set of measurements is sufficient to recover σ.

THEOREM 5.1

If X(x) = (V(x) − λ(x)) Ψ(x) ∈ ℱ and if {x ∈ Ω|Ψ(x) = 0} has measure zero, then V and σ are determined completely from one measurement of Ψ and on the boundary ∂Ω.

Proof

Let {h_l(x) | l ∈ ℤ} be an orthonormal basis for ℱ. We now compute the expansion coefficients of X for this basis. Using (2), integration by parts gives (31) Since X ∈ ℱ we can compute a full expansion . Now we follow the reconstruction procedure described in Section 3 and obtain Ψ in all of Ω using (7). Our assumption on the zeros of Ψ allows us to determine V(x) = X(x)/Ψ(x) + λ(x) almost everywhere. Subsequently τ and σ = τ² are determined by (3a).▪

The application of the above theorem requires the construction of a potential Φ such that X = (V − λ)Ψ ∈ ℱ. An applied current induces a potential Φ and consequently Ψ on ∂Ω. Using Equation (30) we see that the optimal input current which makes the part of X in ℱ as large as possible can be chosen as that which maximizes (32)

6. Further analytic development for constant λ

Although the analysis presented in the previous sections applies for any real valued function λ, the case of constant λ enables us to perform many of the calculations explicitly. Consequently, for the rest of this article we will take λ to be a positive constant and hence the functions {h_l} defined in (23) form an orthonormal set of solutions for the Helmholtz Equation (4). The fundamental solution of Equation (4) for λ > 0 is explicitly known for any dimension n ≥ 2, see 28. For example, where Y₀ is the Bessel function of the second kind.

LEMMA 6.1

For a given domain Ω ⊂ ℝⁿ, the function defined in Equation (24) becomes (33)

Proof

The inner product is given by (34) Using the mean value theorem for the Helmholtz equation 29 we can show that (35) It follows that (36) where . Therefore, (37) ▪

LEMMA 6.2

If λ → 0 then Equation (4) reduces to Laplace's equation and it is straightforward to show that C(γ, λ) → 1. In other words, the scalar product (35) is independent of the regularization parameter γ. Hence, the effective mollifier in (24) and, consequently, the reconstructed X_γ in (29) are independent of the resolution γ.

If we restrict ourselves to simple geometries further explicit calculations are possible.

LEMMA 6.3

Let Ω be a two-dimensional disc of radius R, Ω = {y = (r cos θ, r sin θ) ∈ ℝ² : ‖y‖ ≤ R}, the orthonormal solutions of Equation (4) for λ > 0 are given by (38) (39) where ρ_l are the normalization constants (40) Hence, (41) where (α, ψ) are the polar coordinates of , the centre of the mollifier disc. Furthermore, if the boundary data are sufficiently smooth to guarantee that Ψ ∈ C(∂Ω), and both Ψ′ and are piecewise smooth on ∂Ω, then (42) where a_l, b_l and c_l, d_l are the Fourier series coefficients of Ψ(R, θ) and , respectively.

Proof

It is straightforward to show that are orthogonal solutions to Equation (4). In order to guarantee an orthonormal set of solutions {h_l} we require that and the result given in Equation (39) follows. We can now derive the result for X_γ by substituting in Equation (29) the explicit formula for given in Equation (40). The smoothness assumptions on Ψ, Ψ′ and on the boundary ∂Ω imply that the Fourier coefficients a_l, , and c_l, , where ε > 0 26. From the asymptotic behaviour of Bessel functions, it is straightforward to show that for large l Similar results hold for the terms involving b_l and d_l.▪

7. Numerical implementation on the unit disc

The results of Section 5 suggest that we should be able to use our method to determine an acceptable reconstruction from one measurement only. In principle, this requires an optimal choice of the induced current but in this article we will investigate what can be reconstructed from a single measurement resulting from a standard pattern for the applied current.

The method described in this article is not restricted to particular geometries, but for simplicity, as in the previous section, we consider the unit disc Ω = {y = (r cos θ, r sin θ) ∈ ℝ² : ‖y‖ ≤ 1}. Our general procedure for performing the numerical test is as follows. We start by choosing a conductivity σ that we attempt to reconstruct. To simulate the measured values of the potential on the boundary we have to first solve the direct problem, and in order to avoid inverse crimes we use as forward solver the PDE Toolbox of Matlab which has no connection with the reconstruction method under consideration. Thus, we obtain Φ and Ψ as well as their normal derivatives at 214 equally spaced mesh points on the boundary.

The inversion algorithm is to use our mollifier method to compute X by means of Equation (41) and then follow the step-by-step procedure described in Section 3. Once X is known the calculation of Ψ inside the unit disc is straightforward: (43) The function ζ₀ is computed numerically from the boundary data using the composite trapezium rule: In order to compute the integral on the right-hand side of Equation (42) we note that the integral kernel 𝒢₀ has a weak singularity when (r, θ) = (ρ, ϑ). However, this possible difficulty can be overcome by using special quadrature methods 30 or a subtraction technique 31 as follows: (44) Since relation (43) can be further simplified to where {ρ_k, ϑ_k; w_k} is a set of 172 quadrature points and weights for the unit disc given by Engels in 32. V is then computed by means of Equation (12). Equation (13) can be solved for τ in a stable way, for instance, by means of a Fredholm equation of the second kind with a weakly singular kernel: (45) where the function τ₀ is computed numerically from the boundary data again using the composite trapezium rule: Using the same subtraction technique 31, Equation (44) becomes which can be reduced to a system of linear equations for the values of the function τ at the integration points (ρ_i, ϑ_i), i = 1, 2, …, 172: The above system can be solved using LU decomposition or any other appropriate numerical technique 31. To find the values of the function τ at any point of coordinates (r, θ) we cannot employ the usual Nyström continuation since our integral kernel 𝒢₀V in Equation (44) becomes very large if the point (r, θ) is close to a quadrature point (ρ_k, ϑ_k). In order to overcome this problem, we use a modified Nyström continuation where (ρ_i, ϑ_i) is the closest quadrature point.

8. Numerical examples

In the following numerical examples, we present reconstruction results for data with 1% random errors and λ = 1. A noise level of 1% is reasonable in many circumstances but in some medical applications greater accuracy can be achieved 33. In order to avoid any damping effects in the determination of V using Equation (12) the value of λ cannot be large. Numerical experiments showed that a value of λ = 1 is an appropriate choice. Since the reconstruction is achieved extremely rapidly for any value of the resolution parameter γ, there is no benefit in using an adaptive resolution. Therefore, we are able to use the same resolution γ = 0.1 for all reconstruction points. The optimal choice for the regularization parameter, γ, as given by the L-curve criterion, is approximately 0.1. This is in agreement with the theoretical minimum spatial resolution achievable using our integral equation approach which is derived in 34.

Example 8.1

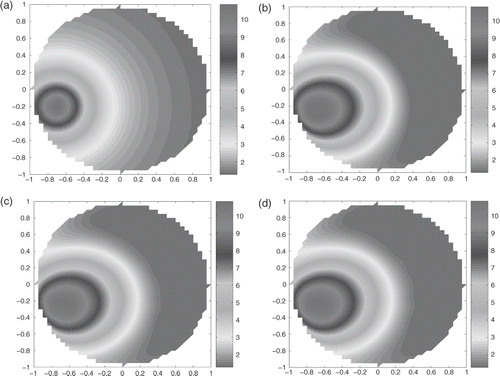
As a first example, we attempt to reconstruct a conductivity distribution consisting of an off-centred high conductivity region within a constant background, see Figure 1a, We present in Figure 1b–d the reconstructed conductivity for data with 1% random errors and different input currents.

Figure 1. (a) The conductivity distribution σ₁(x, y); the reconstructed conductivity, , for data with 1% errors: (b) j(θ) = cos(θ), ; (c) j(θ) = cos(2θ), ; (d) j(θ) = sin(θ), .

Example 8.2

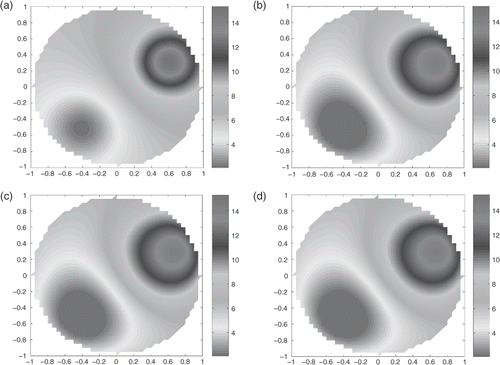
In the second example, we consider a conductivity distribution consisting of two regions, one of high conductivity and other of low conductivity, see Figure 2a,

Figure 2. (a) The conductivity distribution σ₂(x, y); the reconstructed conductivity, , for data with 1% errors: (b) j(θ) = cos(θ), ; (c) j(θ) = cos(2θ), ; (d) j(θ) = sin(θ), .

Example 8.3

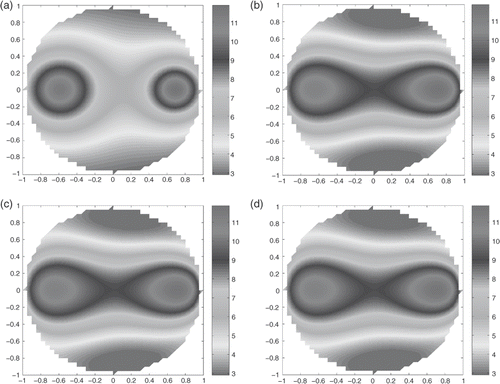
In the third example, we reconstruct a conductivity distribution consisting of two high conductivity regions, see Figure 3a,

Figure 3. (a) The conductivity distribution σ₃(x, y); the reconstructed conductivity, , for data with 1%: (b) j(θ) = cos(θ), ; (c) j(θ) = cos(2θ), ; (d) j(θ) = sin(θ), .

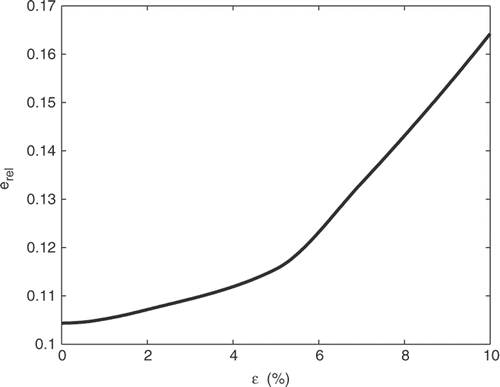
In our numerical experiments, the location of the significant features was well determined but the reconstructed conductivities were smoother than the targets. We also found that the reconstruction algorithm is stable with respect to noise in the input data for error levels of up to 5%. In Figure 4, we plot the L²-relative error, , as a function of noise level ε for the conductivity distribution considered in Example 8.2 and input current j(θ) = cos(θ).

Figure 4. The L²-relative error, , as a function of noise level ε for the conductivity distribution considered in Example 8.2 and input current j(θ) = cos(θ).

9. Conclusion

In this article, we have investigated an application of mollifiers to the inverse conductivity problem. It is based on an assumed knowledge of the boundary values of the conductivity σ and of the potential Φ and their normal derivatives. We reformulate the inverse problem as a linear Fredholm integral equation of the first kind, where the kernel is not given, but can be chosen in a number of ways. The linear problem is efficiently solved by applying the method of mollifiers. Our algorithm allows us to choose an optimal regularization, and since we use the free space Green's function the approach is not geometrically constrained and can be applied to any two- or three-dimensional simply connected domain. Both the theoretical investigations and the numerical experiments indicate that the algorithm gives good reconstructions of smooth conductivity distributions, and that it is quite stable with respect to the noise in the input data.