The modified component method for calculation of orientation distribution function from pole figures

Abstract

The main problem of the quantitative texture analysis is discussed. The sharp texture of nanocrystalline magnesium is under investigation. The well-known harmonic (Roe–Bunge) method of texture determination does not give good results for the materials with low sample symmetry. The robust component fit method for the determination of the orientation distribution function from the set of incomplete X-ray pole figures is used in this work. A unique and reliable solution is achieved.

Keywords:

• quantitative texture analysis
• orientation distribution function determination
• pole figure
• ill-posed problem
• component fit method

AMS Subject Classifications::

• 65D15
• 65K10
• 93B40

1. Introduction

The orientation distribution function (ODF) f(g) defined on the rotation group SO(3) gives full texture description, but it is not measured directly. The experimental pole figures (PF) denoted as are the projections of the ODF to the unit sphere S² 1: The problem of the ODF determination from the set of PFs is ill-posed mainly because of the solution non-uniqueness. This is caused by experimental undistinguishness of the crystallographic directions and . Another source of ill-posedness is the presence of experimental errors. This evokes the solution non-robustness.

The component fit method also referred to as the method of ODF approximation by standard functions is well-known in the quantitative texture analysis (QTA) 2–5. The method is served for the texture investigation in polycrystalline materials. Complete or incomplete PFs obtained by X-ray or the neutron scattering method are used for ODF determination. Various analogues of the Gaussian distribution on the rotation group SO(3) are proposed for mathematical modelling of an ODF and PFs 2,3,6. We used the normal distribution obeying the central limit theorem on the group SO(3) 4,5.

2. Peculiar properties of the experimental PFs

In this study, the specimen of nanocrystalline (submicroscopic) Mg is investigated. This is obtained from initial coarse-grained bar by repeated pushing through an equal-channel angular die at temperature T = 300°C (so–called ECAP procedure). There were six incomplete (i.e. determinated not on the whole sphere) non-normalized X-ray PFs {0002}, , , , and measured in the Institute of Metallurgy (IMET, Moscow, Russia). Distinctive features of the investigated material are the lattice hexagonal symmetry and the lack of specimen orthorhombic symmetry in the presence of fairly sharp texture. The main aim of this study is to determine ODF using the set of PFs. The ODF Fourier–coefficients are used in researching the superplasticity phenomenon of magnesium nanomaterials.

3. Difficulties connected with the material features

The Roe–Bunge 1 method associated with ODF and PFs expansion into Fourier series on corresponding manifolds, does not yield satisfactory results. Firstly, in classic scheme this method reconstructs only the even part of ODF, further the method is extremely sensible to measurement errors, which may reach a degree of 40% in X-ray diffraction experiment (this is the case in our investigation). Lastly, the method does not allow the control of the consistency of values at different PFs. Numerous modifications of this method 7–10 which allow these problems to be more or less overcome, do not work in the case of fairly sharp peaks on the PFs, combined with the specimen low symmetry. In this case, the sharp texture may be approximated only with long fragment of Fourier series, whose number of coefficients is too large.

4. The component fit method. Central normal distributions

The component fit method, which we employ, allows the modelling of the main texture features using a few parameters. Let be the orientation distance between rotations g and g_0k (here signifies the trace of the matrix product). The ODF is supposed to be a superposition of K central normal distributions both peak and axial with unknown weights c_k (c₀–background weight), dispersion parameters ϵ_k, maxima positions g_0k (for axial components with axes also), k = 1, …, K. Here denotes the Legendre polynomial of l–th order whose argument is the product of vectors and . Such kind of ODF generates the PF with the same parameters

These are the PFs which are usually measured in the experiment, so we can estimate unknown parameters mostly by fitting the set of measured PFs. Letting and be directions in the sample and in the space correspondingly, then In this equation, vector is a set of linear parameters (component weights), is a vector of nonlinear (remaining) parameters and are the measurement errors. The last ones depend on many factors, such as number of reflecting grains, non-ideal geometry, defocussing effects, etc. In our work, the measurement errors are assumed to be independent and to have identical accuracy.

The maximum likelihood estimators for unknown parameters of the model are the values which minimize the sum of weighted squared residuals Here the statistical weight reflects the degree of the significance of the measurement at point on . The parameters N_λ should be chosen to normalize the experimental PFs.

Consider first the linear problem. Suppose the texture to be formed of (K − 1) components with almost exactly known maxima positions (the class of correctness for the problem). Then the model ODF is so it generates the model PFs The number of linear parameters to be fitted is K. Let A = (A_sk) be the design matrix 11 of this problem and let vector represent the experimental PF data. Then the minimization of r² yields the normal equations of the least squares problem: In many cases, the normal equations are very close to singularity (the condition number is too large), so a regularization for this linear system is necessary. The regularization is realized by application of singular value decomposition of the design matrix A 12. The condition number of the system is decreased due to thresholding and zeroing small singular values.

In the case of nonlinear parameters the minimization has to be implemented iteratively. Starting from we update the values in each step of the iterations. The initial values are usually solutions of a simpler problem. Consider the quadratic approximation of the common residual where D = (D_pq) is the Hessian matrix In the Levenberg–Marquard method 13, the Hessian D is replaced by some approximation with some heuristic parameter μ, and the updating procedure is given by If , then assigns the new values and μ decreases by some factor, if it is not the case, then retains the old values and μ increases by some factor. Iterations stop when common residual value becomes stable. It should be noted that matrix may become degenerate if the dependence on some particular parameter (t_p) is rather weak, and in some other cases when μ is very small. That is why the regularization of the same type is desirable in the nonlinear case too.

5. Results

Only 2–3 PFs from the set are used for searching the parameters. All the set of model PFs is recalculated after definition of the parameters. The reliability of the model is checked by the response probability (RP)-criterion 1. The RP values for PFs used in the least squares approximation and for unused ones are the same.

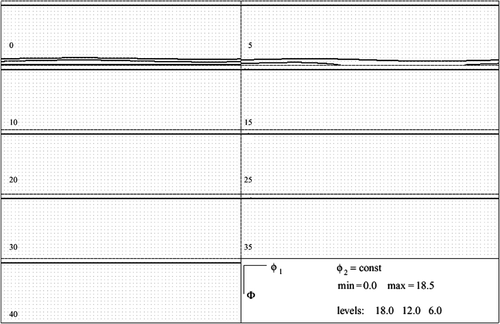
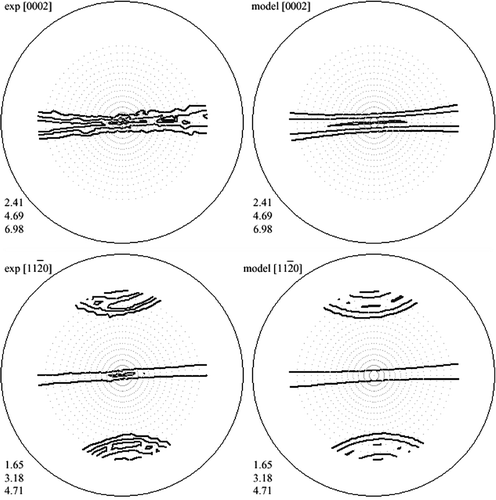
The texture of initial coarse-grained specimen is found to be axial. The complete ODF is equal to the even ODF part (so the odd ODF part is null). In Figure 1 some PFs before equal channel angular pressing are represented, the experimental data are to the left and model data to the right. In Figure 2 the sections of corresponding complete ODF are displayed.

Figure 1. Initial axial texture of coarse-grained specimen: experimental PFs (left) and model PFs (right).

Figure 2. Initial axial texture of coarse-grained specimen: the sections of the complete ODF.

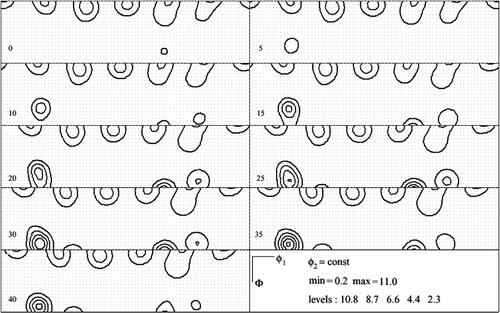
After ECAP procedure, the texture became very sharp and the ODF got significant odd part. In Figure 3, experimental and model PFs after ECAP are shown. Complete ODF and its even part are presented in Figures 4 and 5. The fit component parameters are given in Table 1.

Figure 3. Texture after equal channel angular pressing: experimental PFs (left) and model PFs (right).

Figure 4. Texture after ECAP: the sections of the complete ODF.

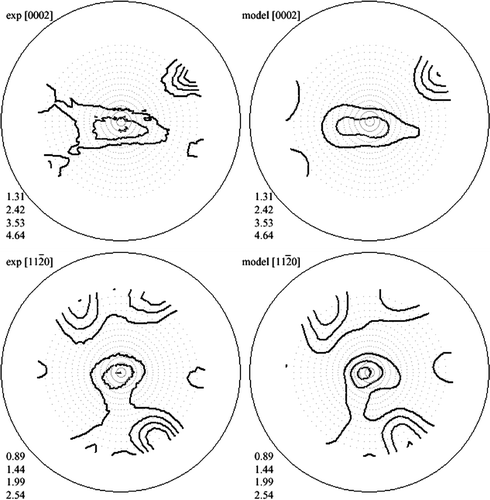
Figure 5. Texture after ECAP: the sections of the even ODF part. The regions of negative values are marked.

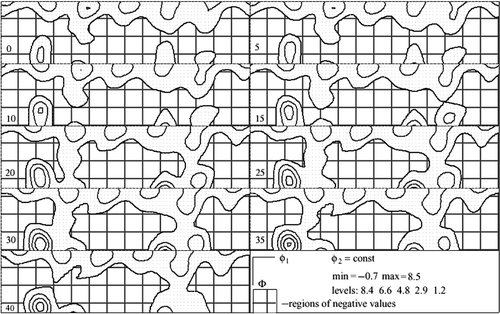
Table 1. The texture parameters after severe deformation.

component	ck		ϕ1, o	Φ, o	ϕ2, o
1	0.17	0.034	259	24	276
2	0.16	0.017	57	83	273
3	0.13	0.026	286	81	265
4	0.11	0.021	127	10	298
5	0.09	0.039	103	44	255
6	0.07	0.013	56	65	256
7	0.07	0.024	239	73	292
8	0.01	0.263	189	18	288
Background	0.19
Note: The components maxima are presented in Bunge angles.

6. Conclusions

The initial texture of the material is axial. Arising after severe deformation, the nanocrystalline texture is formed by eight peak components.

Due to material features the application of harmonic methods for ODF definition requires an enormous quantity of experimental data, which is inaccessible.

Experimental PFs contain large errors that makes the problem of ODF definition very unstable. The robustness is achieved by regularization. Zeroing the small singular numbers in the problem improves the statistic properties of the solution, by making it more smooth and stable.

The even part of ODF contains domains with vastly negative values and the maxima of the even ODF part are 30% less than the maxima of the complete ODF.

The robust component method using central normal distributions is the method of first choice, since it allows matched values of different PFs (to control consistency of different PFs–both used and unused in the approximation procedure), reconstructs full non-negative ODF and operates with a small number of parameters. This method results in an explicit form for the ODF coefficients.

Acknowledgements

This work is supported by the State contract ‘Investigation of textures and plastic anisotropy magnesium nanomaterials’ No. 02.513.11.3340. The authors thank research worker of IMET, V.I. Serebryany, for consultation about experimental part of the work and given PFs.