Application of the Abel inversion in case of a tensor field

Abstract

Abel's integral equations arise in many areas of natural science and engineering, particularly in plasma diagnostics. The axisymmetric physical field is determined using the Abel inversion. Until now, the Abel inversion has been applied almost exceptionally for the determination of scalar fields, i.e. fields, which at a point are characterized by a scalar. In several areas of engineering, the need to determine axisymmetric tensor fields arises, for example by measuring residual stress in axisymmetric glass articles with photoelasticity. In this article, we show how the Abel inversion can be used for the determination of an axisymmetric stress tensor field. The peculiarity in determining the tensor field is that on every ray two integrals of the field are measured and for complete determination of all the components of the stress tensor, equations of the theory of elasticity are used. The method is illustrated by an example.

Keywords:

• Abel inversion
• tensor field
• photoelasticity
• stress analysis
• residual stress

1. Introduction

Abel inversion is a popular technique by which various axisymmetric physical fields are investigated, particularly in plasma diagnostics 1–3. This technology has been applied almost without exception for the determination of scalar fields. At the same time, in physics and engineering, the problem of measuring axisymmetric tensor fields often arises.

In particular cases of photoelastic stress analysis, some stress tensor components can be directly determined with the Abel inversion; for example, by stress measurement in a cylindrical body with no stress gradient in axial direction 4,5. This problem is important by assessing the quality of optical fibres. The basic equation of photoelasticity can be written as (1) where C₀ is the photoelastic constant, σ₁ and σ₂ are principal stresses in the plane perpendicular to the polarized light beam, t is the thickness of the specimen and Δ is optical retardation between light vibrations along the directions of σ₁ and σ₂.

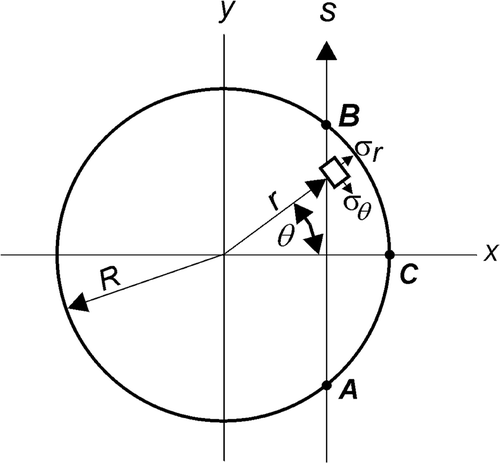
Let us consider passing of polarized light through the cross-section of a cylindrical body with no stress gradient in the direction of its z-axis (Figure 1). In cylindrical coordinates, stress in the cylinder is determined by three stress components: σ_r, σ_θ and σ_z. Due to the photoelastic effect, the cylinder becomes birefringent. One principal birefringence direction (and principal stress direction) is in the radial direction and the other is parallel to the z-axis.

Figure 1. Passing light through the cylinder parallel to the y-axis.

If the polarized light is passed through the cylinder parallel to the y-axis (Figure 1, ray s), optical retardation Δ(x) can be expressed as (2) Equation (2) follows from Equation (1) using notations (3) From the condition of equilibrium of the three-dimensional segment ABC of the thickness h, we have the following: (4) Equation (4) was first derived by Poritsky 6. Physically, Equation (4) means that since the external boundary of the cylinder is free of loads, due to the equilibrium condition in the x direction, integral of the stress σ_x along the line AB must be equal to zero.

Now from Equation (2) follows (5) Since dy can be expressed as (6) Equation (5) can be written in the form (7) The solution of this integral equation is given by (8) Thus, radial distribution of one component of the stress tensor, σ_z(r), can be determined directly with Abel inversion.

The problem of measuring stress in cylindrical bodies arises by investigating residual stress in glass cylinders, fibres and fibre preforms. In this case, the so-called sum rule 4,7 (9) is valid.

On the basis of the sum rule and of the equation of equilibrium, (10) the other stress components can be determined 8, i.e. (11) (12) Thus, all the stress tensor components have been determined. This method has been widely used by measuring stress in optical fibres and fibre preforms 8–10.

If the specimen has general axisymmetric shape and the stresses vary along the z-axis, Abel inversion cannot be applied directly. In this case, the stresses are usually approximated by certain functions (e.g. polynomials), the unknown coefficients of which are directly calculated from the experimental data 11,12. The aim of this article is to show that also in the general case of the measurement of axisymmetric stress with integrated photoelasticity 13,14, the Abel inversion can be applied.

2. The general case of axisymmetric stress distribution

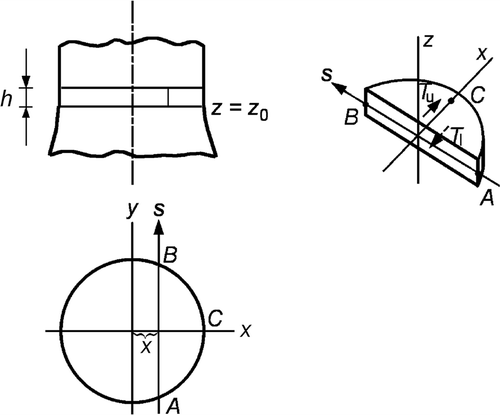
Let us consider determination of the stresses in an axisymmetric transparent object in the case when stresses vary in the direction of the z-axis. The state of stress in a section z = z₀ is determined by the stress tensor components σ_r, σ_θ, σ_z and τ_rz. Let us assume that photoelastic measurements are carried out in two parallel cross-sections of the test object, at z = z₀ and z = z₀ + h (Figure 2). The value of h depends on the stress gradient in the direction of the z-axis and on the precision of the measurements. It is important to reveal information about the stress gradient along the z-axis with sufficient precision.

Figure 2. Investigating an axisymmetric test object in the general case.

In the case of the absence of stress gradient in the z direction, by photoelastic measurements, only optical retardation Δ(x) is recorded since one of the principal directions is parallel to the z-axis, and therefore the principal stress directions are constant on the light ray. In the general case, when the shear stress τ_rz is present, the principal stress directions on the ray s are not constant and actually a rotation of the principal stress directions along the light ray takes place. Due to that optical phenomena are complicated and they are considered in integrated photoelasticity 13,14.

Let us assume that the birefringence of the test object is weak. In this case, optical phenomena can be treated in a simplified way 15,16. By weak birefringence we mean the case when optical retardation Δ(x) is less than about a third of the wavelength. In the case of weak birefringence, the refraction indices n₁ and n₂ in the direction of the principal stresses σ₁ and σ₂ are close to each other (n₁ − n₂ < 10⁻³). It has been shown 15 that in this case by photoelastic measurements in section z = z₀ on every light ray, the parameter of the isoclinic ϕ(x) and optical retardation Δ(x) can be measured and they are related to the integrals of the components of the stress tensor as (13) (14) Let us mention that the main area of the application of integrated photoelasticity is the measurement of residual stress in glass 16. Due to low photoelastic constant C₀ of glass, in glass articles often the birefringence is weak.

Measurements are also carried out in the auxiliary section z = z₀ + h. We denote by and the measurement data in the auxiliary section.

Let us consider equilibrium of the three-dimensional segment ABC (Figure 2) in the direction of the x-axis. We may write (15) where T′ and T are shear forces on the upper and lower surfaces of the segment, respectively, (16) Taking into consideration the relationships (15) and (16), Equation (13) reveals that (17) From Equation (17), the distribution of the axial stress can be determined using the Abel inversion as (18) Equation (14) can be written in the form (19) or (20) From Equation (20), the distribution of the shear stress can be determined using the Abel inversion (21) If σ_z and τ_rz are known, the stress components σ_r and σ_θ can be determined from the equation of equilibrium (22) and from the generalized sum rule 17,18 (23) where D is an integration constant. Equation (23) is to be used when measuring residual stress in glass. If stresses are caused by a mechanical load, instead of Equation (23) the compatibility equation (24) is to be used. Here μ is the Poisson coefficient.

Thus in the general case of the axisymmetric stress tensor field, the axial stress σ_z and shear stress τ_zz distributions are determined from the measurement data with Abel inversion. The other stress components σ_r and σ_θ are determined from the equations of the theory of elasticity. However, in order to use the Abel inversion for the calculation of the stress tensor components, the direct measurement data are to be modified and data from two parallel sections are to be used.

Let us mention that the onion-peeling method 19, a numerical algorithm equivalent to the Abel inversion, can also be used by measuring axisymmetric stress tensor fields 20,21.

3. Example

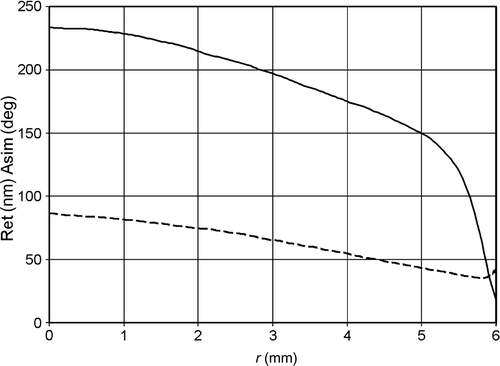
Let us consider measurement of the residual stress in the lower part of the stem of a wine glass (Figure 3). Figure 4 shows distribution of the optical retardation Δ(x) and azimuth of the first principal stress ϕ(x) in the section B–B, which is located at z = 16.61 mm from the lower end of the wine glass. Auxiliary section of photoelastic measurements was located at z + h = 17.61 mm.

Figure 3. (a) Geometry of the wine glass and (b) and fringe pattern in the area A.

Figure 4. Radial distribution of optical retardation Δ(x) (––––) and azimuth of the first principal stress ϕ(x) (–––) in section z = 16.61 mm.

Figure 5 shows distribution of the axial stress σ_z, obtained with Abel inversion from Equation (18), using the onion-peeling method. For comparison, distribution of σ_z, obtained with standard technology of integrated photoelasticity 13,16, is also shown (σ_z has been approximated as a polynomial with three terms). Distribution of stress components σ_r and σ_θ was determined using the equilibrium equation (22) and the generalized sum rule (23) (Figure 6). All stress components are approximated as polynomials with three terms.

Figure 5. Axial stress σ_z distribution, obtained with the onion-peeling method (—) and with polynomial approximation (––––).

Figure 6. Normal stress components in section B–B.

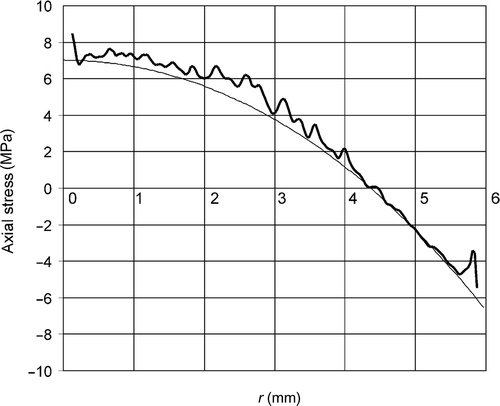
In the case of residual stresses, the average stress in any section should be zero. The average value of the axial stress σ_z, shown in Figure 6, is 0.27 MPa. That makes less than 4% of the maximum value of σ_z. That is an indication of precision of determining the axial stress.

4. Conclusions

It has been shown that the Abel inversion, which is essentially the method for determining scalar fields, can also be applied by investigating tensor fields. The particular case of residual stress measurement in an axisymmetric glass article with integrated photoelasticity has been considered. In this case, on every light ray, two integrals of the stress tensor components can be measured and measurements are to be carried out in two parallel sections. From these measurement data, the Abel integral equations ((18) and 21) for the axial stress and shear stress can be constructed. A peculiarity of the tensor field measurement, in this particular case, is the possibility to use equations of the theory of elasticity as a priori information. Due to that, the stress tensor field can be completely determined. The developed algorithm is illustrated by measuring residual stresses in the stem of a wine glass. An area of application of the generalized Abel inversion is residual stress measurement in axisymmetric glass articles with integrated photoelasticity.

Acknowledgements

The authors appreciate the support of the Estonian Science Foundation (grant No. 7840).