Bioluminescence tomography for media with spatially varying refractive index

Abstract

Biomedical imaging has developed into the level of molecular imaging. Bioluminescence tomography (BLT), as an optical imaging modality, is a rapidly developing new and promising field. So far, much of the theoretical analysis of BLT is based on a diffusion approximation equation for media with constant refractive index. In this article, we study the BLT problem for media with spatially varying refractive index. We introduce a general framework with Tikhonov regularization for this purpose, present its well-posedness and establish the error bounds for its numerical solution by the finite element method. Numerical results are reported on simulations of the BLT problem for media with spatially varying refractive index.

Keywords:

• bioluminescence tomography
• spatially varying refractive index
• inverse problem
• well-posedness
• numerical solution
• error estimate

AMS Subject Classifications:

• 92C55
• 34K29
• 49K40
• 34K28
• 65N15

1. Introduction

With the development of science and technology, these years have witnessed the rapid progress in biomedical imaging. Bioluminescent imaging (BLI), as one of the optical imaging modalities, has its own advantages over traditional imaging methods such as computed tomography (CT), positron emission tomography (PET) 1,2, magnetic resonance imaging (MRI) 3,4 as well as their combinations. For instance, compared to PET and MRI, BLI is low in cost. It is particularly attractive for in vivo applications because no external excitation source is needed, and thus background noise is low while sensitivity is high. For in vivo studies in a big biological object such as human body, BLI is limited to superficial sites owing to the absorption and scattering properties of tissue to light and in this case, PET and MRI are preferred modalities 5.

Table 1. Error for different parameter r.

r	NT = 968, N = 502	NT = 3872, N = 1971	NT = 15,488, N = 7813
0	1.32667e − 3	1.21078e − 3	1.14923e − 3
0.1	1.32654e − 3	1.21022e − 3	6.84920e − 4
0.3	1.32644e − 3	1.20880e − 3	1.12576e − 3
0.5	1.32634e − 3	1.20844e − 3	1.07552e − 3
0.7	1.32619e − 3	1.20680e − 3	1.15209e − 3
0.9	1.32607e − 3	1.20620e − 3	1.15432e − 3
0.99	1.32600e − 3	1.20596e − 3	1.15331e − 3
0.999	1.32600e − 3	1.20511e − 3	1.15330e − 3
1	1.32600e − 3	1.20553e − 3	1.15330e − 3

Bioluminescence tomography (BLT) is a promising BLI because of the possibility of revealing molecular and cellular activity in real time 6,7. Over the past several years, numerous articles have been devoted to the theoretical analysis and numerical simulations of BLT, (see e.g. 8–16 and references therein). The main objective of BLT is to determine the photon density distribution within small-animals or on the surface of some organs from the light measurement on the boundary. With BLT, a bioluminescent source distribution inside a living small animal can be located and quantified in 3D. Because the transport of light in any entity is subject to both absorption and scattering, the accurate representation of the photon transport in a biological tissue is required. The first step of BLT is to determine the optical properties of tissue and this is the issue of a diffuse optical tomography (DOT) problem. In general, the bioluminescent photon propagation in a tissue can be described accurately by either the radiative transfer equation (RTE) or the Monte Carlo model (MCM) 17. However, at the moment, neither is computationally feasible. Usually a diffusion approximation of the RTE is employed when the wavelength of light is in the range of around or bigger than 600 nm 18.

In the literature, the BLT is mostly studied based on a diffusion approximation equation to the RTE with constant refractive index of media. In this work, we consider the BLT problem for media with spatially varying refractive index. Consideration of media with spatially inhomogeneous refractive index can be found in 19–25 and 26,27, the DOT problem for such media is studied.

Let Ω ⊂ ℝ^d be a non-empty, open and bounded set with a Lipschitz boundary Γ ≜ ∂Ω and S^d−1 the unit sphere in ℝ^d. In applications, d = 3. With the diffusion approximation, our BLT problem in spatially varying refractive index media consisting of determining a source function S so that the solution of the following boundary-value problem (BVP): (1) (2) satisfies the measurement condition (3) Here, Ω₀ and Γ₀ are measurable subsets of Ω and Γ, respectively, both with a positive measure. The symbol χ_Ω0 stands for the characteristic function of Ω₀ which takes on the value 1 in Ω₀ and 0 in Ω∖Ω₀. The coefficient , μ_a and are the absorption and reduced scattering coefficients, and n is the refractive index. We denote ∂_ν· for the outward normal derivative on Γ. The measured light flux g on Γ₀ is an element in space L²(Γ₀). In applications, it is unrealistic to have measurement on the entire boundary. In this article, we focus on the situation where Γ₀ is a proper subset of Γ.

As in 12, we can show that the pointwise formulation (1)–(3) of the BLT problem is ill-posed. In this article, the BLT problem is studied through a Tikhonov regularization.

We will need some function spaces. For a set G as Ω, Ω₀ or Γ etc., we denote by W ^m,s(G) the standard Sobolev spaces of degree s and order m with norm ‖ · ‖_m,s,G, and rewrite them as L^s(G) when m = 0. Particularly, H^m(G) represents W ^m,2(G) with corresponding inner product (·, ·)_m,G, norm ‖ · ‖_m,G and seminorm | · |_m,G. Moreover, denote L²(Ω₀) by Q. We further denote by c a constant which may have different value in different place.

The structure of this article is as follows. In the next section, we study the BLT problem with a Tikhonov regularization. We address the well-posedness of the regularized BLT problem and explore the limiting behaviours as regularization parameter tends to zero and infinity. In Section 3, we use the finite element method to approximate the regularized BLT problem and obtain some error estimates. We present some numerical examples in the last section.

2. A formulation for BLT with spatially varying refractive index media

By a standard process, we obtain the following weak formulation of the BVP (1)–(2): (4) where the bilinear form (5) Let Γ₁ = Γ\Γ₀. Since the measurement (3) is available on a proper subset of Γ only, we have |Γ₁| > 0. Define an inner product [·, ·] and the corresponding norm ||| · ||| over H¹(Ω) as follows: It is well-known that the norm ||| · ||| defined above is equivalent to the norm ‖ · ‖_1,Ω.

We will make the following assumption throughout this article:

Assumption (A) Let 0 < b₁ ≤ D ≤ c₁, μ_a > 0, ‖μ_a‖_0,∞ ≤ c₂, n ∈ W^1,∞(Ω), , ‖v‖_0,Ω ≤ c₄|||v|||, and min{b₁, 1/2} > c₁c₃c₄.

Under Assumption (A), it is shown in 26 that for each S ∈ Q, the problem (4) admits a unique and stable solution u ∈ H¹(Ω).

We comment that it is possible to weaken Assumption (A). In applications, the index function n is nearly piecewise constant, i.e. it is piecewise constant in most parts of Ω except in a small neighbourhood of the interfaces of the sub-regions. In other words, there is a small number ϵ > 0 such that for a subset Ω_ϵ of Ω with |Ω_ϵ| ≤ ϵ, ∇n = 0 in . Consider the case of one dimension, d = 1. By a Sobolev embedding theorem (28), there is a constant c₁ such that (6)

Assumption (B) For b₁, c₁, c₃, c₄ and given as in Assumption (A) and (6), .

Proposition 2.1

In the case d = 1, under Assumption (B), for each S ∈ Q, the problem (4) admits a unique solution u ∈ H¹(Ω) such that (7) for some constant c > 0, which is independent of S but may depend on the parameters Ω, D, n and μ_a.

Proof

We apply the Lax–Milgram lemma 28; the only major task is to prove the coercivity of the bilinear form a₁(·, ·). By using the Hölder inequality, (6) and Schwarz' inequality, we have (8) Hence, from Schwarz' inequality together with (8), and by noticing μ_a ≥ 0 in Ω, we have (9) Therefore, we attain the coercivity of the bilinear form a₁(·, ·).▪

We note that Assumption (B) is weaker than Assumption (A) for small ϵ. More delicate arguments are needed to weaken the conditions on data for the coercivity in two/three dimension spaces.

Since the BLT problem in the pointwise form is ill-posed, we will study the BLT problem through a Tikhonov regularization 29–31. We shall only consider the case where the refractive index is constant near the domain boundary. Consequently, the boundary condition (2) reduces to (10)

Combine (3) and the boundary condition (10) to get (11)

From (3), we obtain another mixed boundary condition (12)

We form two boundary value problems: Equation (1) with boundary condition (10) and Equation (1) with boundary condition (12). We then try to minimize the differences between the solutions of these problems with 2 g on the boundary Γ₀. In addition to a₁(·, ·) defined in (5), let

For any T ∈ Q, denote by u₁ = u₁(T), u₂ = u₂(T) ∈ H¹(Ω) the corresponding weak solutions: (13) (14) Under Assumption (A), both problems are uniquely solvable. Moreover, we have the bound (15)

For r ∈ [0, 1] and α ≥ 0, we introduce the following cost functional: (16)

Then we define a general regularized BLT problem as follows.

Problem 2.2

Find S_r,α ∈ Q_ad such that (17) where Q_ad is a convex closed subset of the space Q.

We comment that here we have introduced a family of regularized BLT problems, depending on a parameter r ∈ [0, 1]. The conventional choice for solving the BLT problem is r = 1. However, the numerical results in the final section suggest that a proper choice of the parameter r leads to an improvement in the reconstruction accuracy compared to the conventional choice, with only a slight increase in the computational effort since the stiffness matrix and the load vector in the finite element solution of the problem (13) can be used in constructing the finite element system for the problem (14).

By extending the arguments used in 10,12, we can show the following main properties of Problem 2.2.

Proposition 2.3

For any α > 0 and r ∈ [0, 1], Problem 2.2 has a unique solution S_r,α ∈ Q_ad which can be characterized by a variational inequality (18)

When Q_ad is a subspace of Q, the inequality reduces to a variational equality for any T ∈ Q_ad

The solution S_r,α depends continuously on the measurement g ∈ L²(Γ₀), the regularized parameter α > 0, coefficients D ∈ L^∞(Ω), n ∈ W^1,∞(Ω) and μ_a ∈ L^∞(Ω).

Assume that 0 ∈ Q_ad. Then ‖S_r,α‖_0,Ω0 → 0 as α → ∞.

Assume taht 𝒮_r ⊂ Q_ad, the solution set of Problem 2.2 for α = 0, is nonempty. Then, S_r,α → S_r,* as α → 0⁺, where S_r,* ∈ 𝒮_r satisfies

We also have the following result.

Proposition 2.4

Let α > 0. Denote by S_0,α and S_1,α the unique solutions of Problem 2.2 for r = 0 and r = 1, respectively. Then S_r,α → S_0,α in Q as r → 0⁺, S_r,α → S_1,α in Q as r → 1⁻.

Proof

We only prove the second assertion, i.e. S_r,α → S_1,α in Q as r → 1⁻. The first assertion can be proved similarly. For each parameter α,

So the sequence {S_{r, α}}_r is bounded, and there is a subsequence denoted again by {S_r,α}_r and an element S_*,α ∈ Q, such that Apparently, S_*,α ∈ Q_ad. Denote u_1,r = u₁(S_r,α), u_2,r = u₂(S_r,α). Then (19) (20)

From relations (7) and (15) as well as the boundedness of sequence {S_r,α}_r, we gain the boundedness of sequences {‖u_{1, r}‖_{1, Ω}}_r2 and {‖u_{2, r}‖_{1, Ω}}_r2. Consequently, resorting to a further subsequence if necessary, there are u_1,*, u_2,* ∈ H¹(Ω) such that

Particularly, u_1,r ⇀ u_1,* in L²(Γ) and u_2,r ⇀ u_2,* in L²(Γ₁), as r → 1⁻. Then pass through r → 1⁻ in (19) and (20) to get

Hence, u_1,* = u₁(S_*,α) and u_2,* = u₂(S_*,α), that is,

Letting r → 1⁻ in (18), we have (21) which gives S_*,α = S_1,α from the uniqueness of the solution of Problem 2.2 for r = 1. Therefore, the entire sequence {S_r,α}_r converges weakly to S_1,α as r → 1⁻, from the independence of the choice of subsequences in the arguments above. Strong convergence is shown as follows. Take T = S_1,α in (18) and T = S_r,α in (21), and add the two resulting inequalities to obtain

We conclude the strong convergence of {S_r,α}_r to S_1,α as r → 1⁻.▪

3. Numerical approximation of BLT

In this section, we consider numerical approximation of Problem 2.2. The standard FEMs are applied to discretize the BLT problem. Let {𝒯_h}_h be a regular family of triangulations over domain with meshsize h > 0. For each triangulation 𝒯_h = {K}, define the linear finite element space . Here 𝒫_k denotes the space of all polynomials of degree ≤ k. Assume that {𝒯_0,H}_H is a regular family of triangulations of with meshsize H. Define the space Q^H = {T ∈ Q ∣ T|_K ∈ 𝒫₀(K) ∀K ∈ 𝒯_0,H} and set . Let Π^H: Q → Q^H be an orthogonal projection operator defined by (22)

Define , by

Then we introduce a discrete cost functional (23)

Problem 3.1:

Find such that

Results similar to Propositions 2.3 and 2.4 hold for Problem 3.1.

The solution of Problem 3.1 is characterized by the inequality (24)

We now provide a sample error bound for the approximate solution of Problem 2.2. For this purpose, assume Γ ∈ C^1,1, D ∈ C ^0,1, n ∈ C^1,1 and g ∈ L²(Γ₀). Then for the solutions of the BVP (13) and (14), we have the regularity u₁(T) ∈ H²(Ω) and u₂(T) ∈ H^3/2(Ω) 32. The following error bounds are useful 12: there exists a constant c > 0 independent of α, h and H such that for any T ∈ Q,

From these error bounds, together with the trace inequality for any v ∈ H¹(Ω), we obtain (25) (26)

Therefore, similar to the proof of Lemma 4.7 in 12, we have (27) (28)

Denote

Then we have the following error bound.

THEOREM 3.2

There exists a constant c > 0 independent of α, r, h and H such that (29)

Proof

Substitute in (18), T^H = Π^HS_r,α in (24), and add the two resulting inequalities to obtain

Applying (22), (27) and (28), we obtain (29).▪

Under additional assumptions, we can deduce more concrete error bounds from Theorem 3.2. For instance, if Q_ad is a bounded set in the space Q, then there is a constant c > 0 independent of α, h and H such that

We note that as we have seen in Section 3 that with proper choice of α related to h and H, we can show the convergence of to S_r,* as h, H, α → 0⁺, assuming that 𝒮_r is nonempty, where S_r,* has minimal L²-norm among the solution set of Problem 2.2 with α = 0.

4. Numerical experiments

In this section, we will show some simulation results. We limit ourselves to the two-dimensional case.

4.1. Implementation detail

Let ϕ_i(x) ∈ V^h be the nodal basis functions of the finite element space V ^h associated with the grid nodes x_i, i = 1, 2, …, N (N is the number of nodes of the triangulation 𝒯_h). Then, , , with and , respectively. Denote triangulation 𝒯_0,H = {K_0,l}, l = 1, 2, …, N₀ (N₀ is the number of elements of triangulation 𝒯_0,H), that is, , then an approximate light source S^H ∈ Q^H has form S^H ∣_K0,l = s_0,l with s_0,l ≥ 0, l = 1, 2, …, N₀. Assume that 𝒯_0,H and 𝒯_h are consistent, that is, 𝒯_0,H can be viewed as a restriction of the triangulation 𝒯_h on . We further let the end points of Γ₀ be grid points of the triangulation 𝒯_h. For the ease of our statement, denote I = {1, 2, …, N}, I₀ = {1, 2, …, N₀}, I_b = {i ∈ I ∣ x_i ∈ Γ}, with and the number of the grid nodes on the boundary , and with the number of the grid nodes on the boundary . Moreover, define where and is the support of the basis function ϕ_i. We further denote by U ⁽¹⁾ and U ⁽²⁾ the vectors and , respectively, and again by S the vector (s₁, s₂, …, s_N0)^t, where a superscript t stands for transposition. For numerical simulation, b_ij is computed as follows.

Here (ρ(x))_GK denotes the value of function ρ at the gravitational centre of the triangle K. To obtain the representation of matrix form, we let where we use the same symbol g for the function g(x) and the vector with . Then we have the systems (30)

We can solve the linear system (30) with any fast methods including direct and iterative methods. In our experiments, we use direct method when the system size is relatively small and use bi-conjugate gradient method (BiCG) 33 when the system size is large. Consequently, the functional reduces to where |K_0,l| is the area of the element K_0,l.

Define , which is spanned by . Express the solutions U ^(k) (k = 1, 2) of the linear systems (30) as U ⁽¹⁾ = M¹S and U ⁽²⁾ = η + M²S with and η a vector of N components. Let We further have Then Problem 3.1 reduces to the following quadratic programming problem: (31)

4.2. Numerical results

In our simulations, the problem domain Ω ⊂ ℝ² is a circle centred at the origin with radius 20 mm, the reduced scattering coefficient , the absorption coefficient μ_a = 0.020, and the refractive index

With a given permissible region Ω₀, we use Q_ad = {S ∈ Q | S ≥ 0 a.e. in Ω₀} for the admissible set of the light source function. We assume that the observations are available on part of the boundary Γ₀ = {(x, y)| x² + y² = 20²; x ≥ 0}, the measurement g on Γ₀ is polluted by noise with level 10%, and the Tikhonov regularization parameter α = 1 × 10⁻⁵. We use Delaunay elements for the triangulations. For a triangulation, denote by NT and N the numbers of elements and nodes.

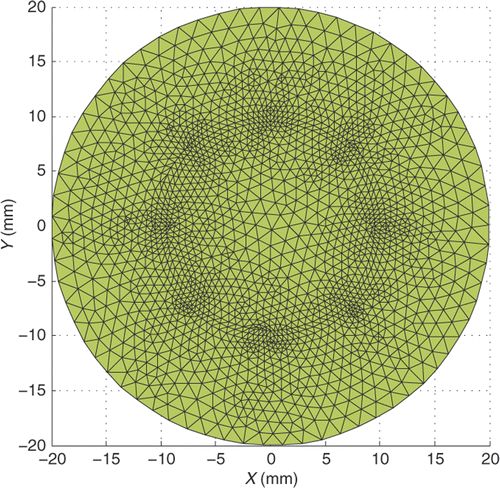
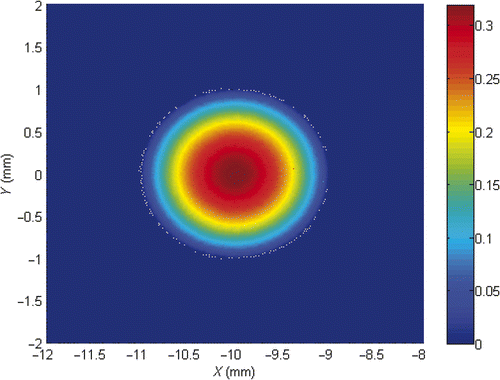
We first consider a single light source reconstruction problem. A light source of density S(x, y) = (1 − (x + 10)² − y²)/π is placed on a circle centred at (−10, 0) with radius 1 mm. Let the permissible region Ω₀ = {(x, y) | (x + 10)² + y² < 2²}. We show the triangulation and the exact light source function S in Figures 1 and 2. Figures 3–5 show approximate light source for partition with NT=968, N=502, NT=3872, N=1971 and NT=15488, N=7813, respectively. Each figure contains four pictures corresponding to r = 0, r = 0.5, r = 0.9 and r = 1. We conclude from these figures that the smaller the meshsize is, the better the light source reconstruction.

Figure 1. Triangulation of for a single light source problem.

Figure 2. (Available in colour online). Exact single light source.

Figure 3. (Available in colour online). Reconstructed single light source with NT = 968, N = 502 for r = 0, r = 0.5, r = 0.9 and r = 1.

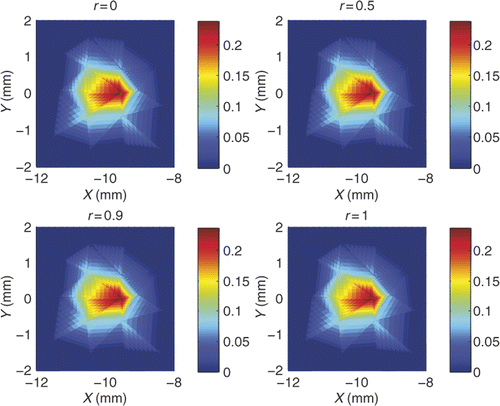
Figure 4. (Available in colour online). Reconstructed single light source with NT = 3872, N = 1971 for r = 0, r = 0.5, r = 0.9 and r = 1.

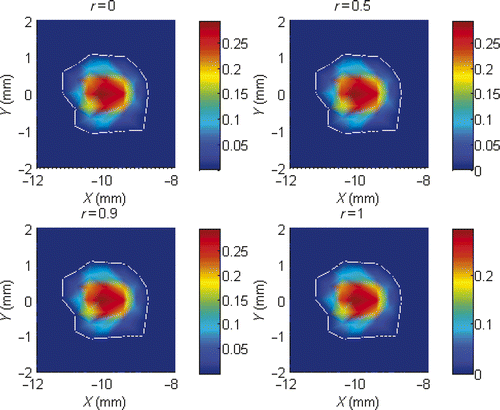
Figure 5. (Available in colour online). Reconstructed single light source with NT = 15488, N = 7813 for r = 0, r = 0.5, r = 0.9 and r = 1.

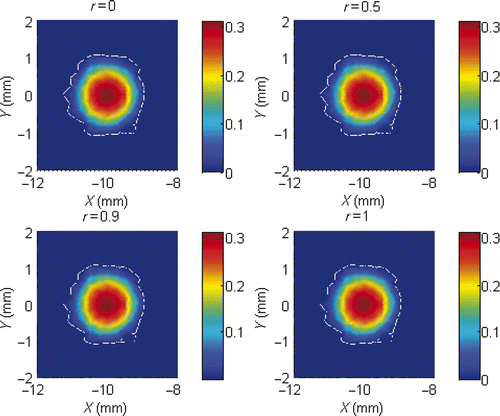
To see the influence of the parameter r on the accuracy of the numerical solution, we report in Table 1 the numerical solution errors for several choices of the parameter. It can be seen from Table 1 that for a fixed triangulation, error in approximate light source gets smaller slightly when the parameter becomes bigger until near r = 1. We also observe that it is possible to adjust the value of the parameter r so as to achieve better accuracy of the approximate light source function than the conventional formulation (r = 1, corresponding to a single forward boundary value problem). How to determine an optimal value for the parameter r is a topic worth further investigation. The numerical results also suggest that generally the conventional choice r = 1 is quite satisfactory.

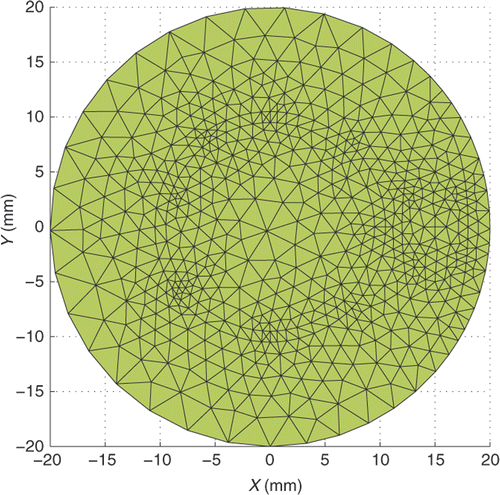
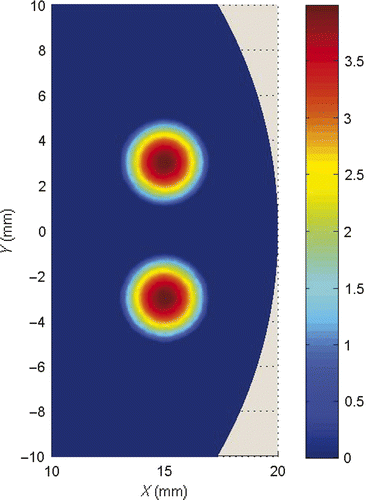
We then consider a reconstruction problem with two distinguish light sources. Place two circular light sources with radius 2 mm at (15, 3) and (15, −3), with densities 4 − (x − 15)² − (y − 3)² and 4 − (x − 15)² − (y + 3)², respectively. We choose the permissible region Ω₀ = {(x, y) | (x − 15)²/9 + y²/100 < 1}. The triangulation and the exact light source function are plotted in Figures 6 and 7. Reconstructed light source functions are shown in Figures 8 and 9 with partition of 1225 triangle elements and 637 nodes, and partition of 4900 triangle elements and 2498 nodes respectively.

Figure 6. Triangulation of for a multiple light source problem.

Figure 7. (Available in colour online). Exact multiple light source.

Figure 8. (Available in colour online). Reconstructed multiple light source with 1225 elements and 637 nodes, r = 1.

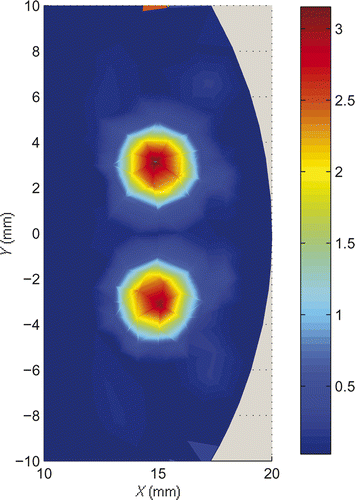
Figure 9. (Available in colour online). Reconstructed multiple light source with 4900 elements and 2498 nodes, r = 1.

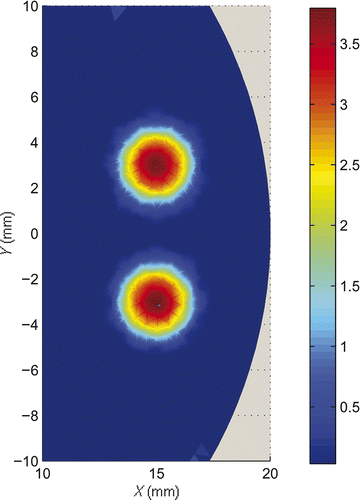
We observe that in all our numerical simulations, the light source functions are well reconstructed.

Acknowledgements

This work was supported by the National Science Foundation of China under Grant No. 10871179 and the National Basic Research Programme of China under Grant No. 2008CB717806.