Fast reconstruction of harmonic functions from Cauchy data using integral equation techniques

Abstract

We consider the problem of stable determination of a harmonic function from knowledge of the solution and its normal derivative on a part of the boundary of the (bounded) solution domain. The alternating method is a procedure to generate an approximation to the harmonic function from such Cauchy data and we investigate a numerical implementation of this procedure based on Fredholm integral equations and Nyström discretization schemes, which makes it possible to perform a large number of iterations (millions) with minor computational cost (seconds) and high accuracy. Moreover, the original problem is rewritten as a fixed point equation on the boundary, and various other direct regularization techniques are discussed to solve that equation. We also discuss how knowledge of the smoothness of the data can be used to further improve the accuracy. Numerical examples are presented showing that accurate approximations of both the solution and its normal derivative can be obtained with much less computational time than in previous works.

Keywords:

• alternating method
• Cauchy problem, Laplace equation
• Nyström method
• second kind boundary integral equation

AMS Subject Classifications::

• 35R25
• 65N20
• 65N35
• 31A10
• 31A05

1. Introduction

In many engineering problems for fluid and heat flow, such as in non-destructive testing and tomography, the governing model is the Laplace equation and overspecified data is given on a part of the boundary of the solution domain in the form of the solution and its normal derivative, see, for example, 1,2. This is termed a Cauchy problem, and even if a solution exists to it, usually it cannot be numerically calculated via classical methods since it is ill-posed, thus highly sensitive to measurement errors in the data.

To formulate our model, let Ω be a bounded domain in R² with Lipschitz boundary Γ and let Γ_C be a non-empty (open) arc of Γ. We are interested in finding a harmonic function u such that this function and its normal derivative satisfy given Cauchy conditions on Γ_C, and this means that u solves (1) where f_C and g_C are given functions, and ν is the outward unit normal to the boundary. Note that uniqueness of the solution u is well-established, see for example 3,4. We shall assume that data are given such that there exists a solution.

Due to the importance of the model (1), there are many different numerical methods in the literature for this Cauchy problem. In 1989, Kozlov and Maz'ya 5 proposed a procedure denoted as the alternating iterative method for solving Cauchy problems for general strongly elliptic and formally self-adjoint systems in bounded domains. One of the advantages of this method is that the governing partial differential operator is preserved and the regularizing character is achieved by appropriate change of the boundary conditions. In 6, the alternating iterative method is applied and investigated for Cauchy problems for the equations of anisotropic elasticity.

The alternating method gives relatively accurate numerical approximations and is suitable for use in practical applications. This has been verified in numerous papers, see for example 7–17. The number of iterations needed for an accurate approximation in this procedure can be large and time-consuming; in 18, it was noted that around 50,000 iterations were needed to get a reasonable approximation in the Stokes flow and it took more than one day to perform these computations using the boundary element method. Of course, the Stokes flow in itself is a more complex phenomena to numerically simulate than stationary heat flow but also for the Laplace operator the alternating method can be time-consuming. Note that there are various relaxation techniques to improve the rate of convergence, see 19,20, but the choice of relaxation parameters can be difficult.

However, in each iterative step of the alternating method, mixed problems are solved for the governing differential operator but only the solution or its normal derivative on the boundary of the solution domain are of interest. Thus, it should be possible to considerably speed up the procedure using boundary integral techniques and Nyström discretization schemes, and this possibility will be explored in this work.

Recently, see 21, a highly accurate and efficient method based on Fredholm integral equations of the second kind was proposed to solve mixed boundary value problems for the Laplace equation and the biharmonic equation. We employ this method for the alternating procedure and show that it is easy to do millions of iterations in only few seconds on an ordinary computer. The approximations are at least as accurate as those earlier reported in the literature and which are mainly based on the boundary element method. We then rewrite the Cauchy problem as a fixed point equation on the boundary, and discuss some additional techniques to solve that equation. In particular, to further improve the accuracy, we show how knowledge of the smoothness of the solution and its normal derivative on the boundary can be used to restrict the solution space, decrease the number of degrees of freedom, speed up the computations and increase stability. With such additional information, we can accurately reconstruct both the solution and its normal derivative on the remaining part of the boundary using little computational cost.

We point out that, in principle, in 2-dimensions one can apply conformal mappings to solve boundary value problems for the Laplace equation. We do not invoke this, however, since we are interested in methods that can be generalized to 3-dimensional domains.

The outline of the article is the following. In Section 2, we introduce some notation and function spaces. In Section 3, we recall the alternating method and some of its properties. Recursive forms of these methods in terms of updating boundary data are given in Section 4, and we also present direct methods for the Cauchy problem. Geometry and parameters for the numerical investigations are presented in Section 5. In Section 6, the numerical implementation of the alternating procedure is discussed, together with the integral equation method used, and the discretizations employed. To further improve the results and efficiency, construction of suitable initial guesses of the solution on remaining part of the boundary Γ are given in Section 7, together with ideas on incorporation projections into the procedure. The final results show that accurate approximations can be obtained both for the solution and its normal derivative on the remaining part of the boundary using very little computational time.

2. Notation and function spaces

Let Ω, Γ and Γ_C be as above and define , and note that Γ_U is the open part of the boundary where the solution and its normal derivative are unknown in (1). As usual, H¹(Ω) is the Sobolev space of real-valued functions in Ω with finite norm (2) where ∇ = (∂_x1, ∂_x2). By , we denote the subspace of functions of H¹(Ω) that vanish on Γ. The space of functions in H¹(Ω) vanishing on Γ_C (Γ_U) is denoted by .

The space of traces of functions from H¹(Ω) on Γ is denoted by H^1/2(Γ). This space is equipped with the norm (3) where dσ is an element of arc-length. Restrictions of elements in H^1/2(Γ) to the boundary part Γ_C (Γ_U) constitute the space H^1/2(Γ_C) (H^1/2(Γ_U)), where the norm is defined by (3) with Γ replaced by Γ_C (Γ_U).

We also use the space that consists of elements from H^1/2(Γ) vanishing on Γ_U. This is then a subspace of H^1/2(Γ) and one of the equivalent norms in this space is (4) In the similar way, is defined.

3. The alternating method and some of its properties

To present the alternating method of 5 for finding a stable approximation to (1), we introduce the following mixed boundary value problems: (5) and (6) The procedure is then as follows:

i.	The first approximation, u1, to u of (1), is obtained by solving (5) with gU = g0, where is an arbitrary initial guess of the normal derivative on ΓU.
ii.	Given that u2k−1 has been constructed, we find u2k by solving problem (6) with fU = fk−1/2, where fk−1/2 = u2k−1|ΓU.
iii.	The element u2k+1 is obtained by solving (5) with gU = gk, where (7)

In the case of exact Cauchy data the alternating procedure continues by iterating in the last two steps.

Note that the alternating method puts few restrictions on the governing operator and the solution domain. In fact, it can be applied to strongly elliptic self-adjoint operators in Lipschitz domains.

In the remark below we give another version of the alternating method and, to distinguish between the various sequences obtained, we use the index k for the normal derivative on Γ_U and k + 1/2 for function values on Γ_U in the first method. The opposite notation, k for function values and k + 1/2 for derivatives on Γ_U, is used in the second method.

Remark 1

We point out that instead of starting the alternating procedure by guessing the normal derivative on Γ_U and solving (5), one can instead make a guess of the function itself on Γ_U, say f_U = f₀, and start by solving (6). The scheme is then as follows:

i.	The first approximation, u1, to u of (1), is obtained by solving (6) with fU = f0, where f0 ∈ H1/2(ΓU) is an arbitrary initial guess of the solution on ΓU.
ii.	Given that u2k−1 has been constructed, we find u2k by solving problem (5) with gU = gk−1/2, where .
iii.	The element u2k+1 is obtained by solving (6) with fU = fk, where (8)

We will refer to this latter method as the second version of the alternating procedure.

In Section 4, we rewrite these schemes in term of recursions in boundary data on Γ_U and then these recursions will be numerically implemented and investigated in Sections 6 and 7.

3.1. Convergence

For the convergence of the alternating method, we have the following result 5,6:

THEOREM 3.1

Let f_C ∈ H^1/2(Γ_C) and be chosen such that (1) has a solution u ∈ H¹(Ω). Let u_k be the k-th approximate solution in the alternating procedure. Then (9) for any initial data element .

Note that using trace estimates, we also get convergence of u_k|_ΓU to the correct solution. Moreover, as was pointed out in 9, in the interior, we have convergence also of derivatives of higher order.

COROLLARY 3.2

Let the assumptions of Theorem 3.1 be fulfilled and let Ω′ be a domain with . Then, for l = 1, 2, …, (10) for any initial data .

To see this, note that since u_k − u satisfies system (1), we can use local estimates for the Laplace equation, and get (11) Then the results of the corollary follow by referring to Theorem 3.1.

Let us briefly recall the ideas in 5,6 of proving Theorem 3.1, since this gives a reformulation of the Cauchy problem that we shall use for effective numerical implementation.

Let u₁ be the solution to (5), for given functions g_U and f_C = 0. Then let u₂ be the solution to (6) with g_C = 0 and f_U = u₁ on Γ_U. The operator is defined by (12) This is a well-defined linear operator. In the similar way, let v₂ be the element obtained from the second approximation in the alternating procedure, with initial guess g_U = 0, and define the element G_NN(f_C, g_C) by (13) The Cauchy problem (5) is equivalent with the fixed point equation (14) Then in the alternating procedure when G_NN(f_C, g_C) = 0, one can show that . Thus, for the convergence one has to investigate properties of the operator B_NN. From 5, it can be shown that B_NN is self-adjoint, non-negative, non-expansive, and that the number one is not an eigenvalue. This implies convergence of the procedure (for non-discretized operators) in the Sobolev space stated in the above theorem.

Remark 2

For the second version of the alternating method, now let u₁ be the solution to (6), for given functions f_U and g_C = 0 and let u₂ be the solution to (5) with f_C = 0 and (15) The operator B_DD : H^1/2(Γ_U) → H^1/2(Γ_U) is defined by (16) Then let v₂ be the element obtained from the second approximation in this version of the alternating procedure, with initial guess f_U = 0, and define the element G_DD(f_C, g_C) by (17) The Cauchy problem (5) is then equivalent with the fixed point equation (18)

To prove convergence in this case, let Sf_U be the restriction of the normal derivative to Γ_U of the solution to the Laplace equation in Ω with Dirichlet conditions u = f_C on Γ_C and u = f_U on Γ_U. Starting the alternating method with g₀ = Sf₀, the second step and onwards will be precisely like starting the second version of the alternating procedure with initial guess f_U = f₀. Thus, from Theorem 3.1, convergence is settled also for the second version of the alternating procedure. Corresponding to (14) and (18), we have the equation (19)

4. Recursive schemes of the alternating methods

4.1. Recursion in the original alternating method

We can rewrite the alternating procedure in various ways for an effective numerical implementation. In particular, one only needs to construct function values or normal derivatives on the boundary part Γ_U. To exemplify this, let B_NN and G_NN be defined by (12) and (13), respectively. Then the original alternating method can be written in the form (20) where (21) and g₀ is the initial guess. The element g₀ is usually taken to be zero; another natural guess is G_NN(f_C, g_C). The evaluation of the operator B_NN involves the solution of two mixed boundary value problems corresponding to steps (ii) and (iii) in the alternating procedure. In fact, the operator B_NN can be split into a product of two operators. To show this, let (22) where u solves (5) with f_C = 0 and g_U = g. Furthermore, let (23) with u solving (6) with g_C = 0 and f_U = f. Then one can check that (24) We discuss how this operator can be efficiently discretized and numerically evaluated in Sections 6 and 7.

Similarly, we introduce (25) where v solves (5) with f_C = f and g_U = 0, and (26) with u solving (6) with g_C = g and f_U = 0. Note that (27) and (28)

Given the normal derivative g_k on Γ_U, we can obtain the function value f_k+1/2 by performing a single-step as (29)

We can also find a representation for the function values f_k+1/2 on Γ_U corresponding to (20). This formula can be obtained by using the operators for the second version of the alternating method and will be derived in the next section.

We point out that in a direct method instead of iterating we can rewrite (14) as (30) and solve for g. Then, if needed, simply compute f using (29).

4.2. Recursion in the second version of the alternating method

Let B_DD and G_DD be defined by (16) and (17), respectively. Then the second version of the alternating method can be written in the form (31) where f_k = u_2k|_ΓU and f₀ is the initial guess. The element f₀ is usually taken to be zero, another natural guess is G_DD(f_C, g_C). One can check, using the operators introduced in the previous section, that (32)

Given the function value f_k on Γ_U, we can obtain the normal derivative g_k+1/2 from (33)

There is also a formula for the normal derivative using B_NN. Simply use g_1/2 from (33) in (20), with, for example, f₀ = 0.

In the same way, there is a formula for function values in the original alternating method using B_DD and it is obtained by using f_1/2 from (29) in (31) with, for example, initial guess g₀ = 0.

We point out also here that in a direct method instead of iterating, in the second version of the alternating method, we can rewrite (18) as (34) and solve for f. Then, if needed, simply compute g using (33).

Remark 1

Since solving the Cauchy problem (1) is equivalent of finding a fixed point of Equation (14), then according to 22, Chapter 3, Section 3, the discrepancy principle can be employed as a stopping rule for the alternating method in the case of noisy data. Thus let the noisy data and , where δ > 0, be given such that (35) Then if k = k(δ) is the smallest integer with (36) for some given b > 1, then converges to the exact solution of (1) when δ → 0.

Remark 2

For the second version of the alternating method, we have Equation (18) to solve. Thus, one can apply the discrepancy principle also for that method.

5. Test geometry, software and hardware for the numerics

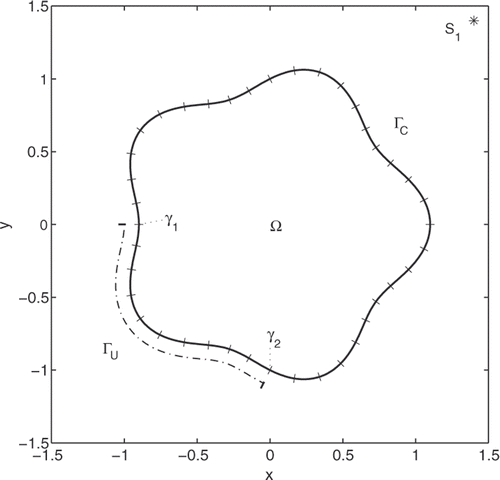
To keep the notation short we make no distinction between points in the real plane R² and points in the complex plane C; all points will be denoted z or τ. We mainly use the same geometry throughout the numerical experiments, namely an interior domain with boundary parametrization (37) see Figure 1, but we shall also vary this geometry to see how other geometries influence the numerical results. In fact, for the integral equation method outlined in the next section, the main requirement on the solution domain is that its boundary can be parametrized by a piecewise smooth function τ(t).

Figure 1. The solution domain Ω with boundary Γ = Γ_U ∪ Γ_C given by (37) and (38). The closure of the arcs Γ_U and Γ_C meet at the two points γ₁ and γ₂. A mesh of 40 quadrature panels is constructed on Γ, 10 of which are located on Γ_U. A source S₁, for the generation of Cauchy data via (39), is marked by ‘*’.

The boundary given by (37) is simple to produce, yet not trivial since its curvature is varying. The two arcs Γ_U and Γ_C are (38) The two points where the closure of Γ_U and Γ_C meet are γ₁ = τ(π) and γ₂ = τ(−π/2), and are referred to as singular boundary points. The Cauchy data will be chosen compatible with the harmonic function (39) where S₁ = 1.4 + 1.4i, see Figure 1.

All numerical experiments presented are performed in MATLAB version 7.6 and executed on an ordinary workstation equipped with an Intel Core2 Duo E8400 CPU at 3.00 GHz.

6. An integral equation method for the mixed problems

The numerical solution to the mixed problems (5) and (6) can be obtained by a recently developed integral equation based solver 21, which we now briefly review.

6.1. Fredholm second kind equations

Fredholm second kind integral equations (40) are constructed for (5) and (6), corresponding to Equations (22)–(23) in 21. Here superscript ‘(1)’ refers to (5) and superscript ‘(2)’ refers to (6) and K^(j) are integral operators. Due to the singular boundary points, K^(j) is not compact, but each K^(j) can be decomposed into the sum of a compact and a non-compact operator. The right-hand sides in (40) are (41) (42) The solutions sought, u(z) or ∂u(z)/∂ν with z ∈ Γ_U, can be obtained from the layer density ρ^(j)(τ) via integral representations that are a mix of single-, double- and quadruple-layer potentials, see further the Equations (21) and (24) in 21.

6.2. Discretization and transformation of the integral equations

The integral equations (40) are discretized using a Nyström scheme, relying on composite 16-point Gauss–Legendre quadrature as the basic quadrature tool; for more on Nyström schemes, see 23, Chaper 4]. A number n_Λ = 40 of quadrature panels, equisized in parameter, are, for this purpose, placed on Γ, see Figure 1. This corresponds to N = 640 discretization points on Γ, of which N_U = 160 points are located on Γ_U and N_C = 480 points are located on Γ_C. This is more than sufficient for full resolution, that means achieving the highest possible accuracy in the solver given the boundary and the boundary conditions of Figure 1. Hypersingular and logarithmic integral operators are discretized using a mix of two techniques denoted as local regularization and panelwise evaluation, respectively, see Section 2 of 21.

Upon discretization, the integral equations (40) are transformed, using a recursive compressed inverse preconditioning technique, to resemble the discretizations of Fredholm second kind integral equations with operators that are everywhere compact. The result can be written as (43) where all matrices have size N × N, I is the identity matrix, K^°(j) corresponds to the discretization of a compact integral operator, R^(j) is a compressed weighted inverse, is a discrete transformed layer density and h^(j) is the discretized right-hand side (function values at the discretization points), see further Equation (34) of 21.

6.3. Post-processor

Once (43) is solved for , discrete Neumann–Dirichlet and Dirichlet–Neumann maps can be computed in post-processors (44) where L^(j) are N × N matrices. If the right-hand sides h^(j)(z) of (40) are piecewise smooth, then the scheme given in 21 can produce highly accurate results irrespective of what the smoothness of the solution is in Ω.

When N is large and one only has to solve mixed problems a small number of times it is appropriate to use an iterative solver for (43) and implement the action of the post-processor (44) without explicitly forming the matrices L^(j). This is the approach taken in Equations (39) and (49) of 21. In the present context, where N is small and we may wish to solve millions of mixed problems, it is effective in the end to construct the N × N matrices (45)

Let the matrices B_DN, G_DC, B_ND and G_NC be discretizations via the above schemes of the operators B_DN, G_DC, B_ND and G_NC of (22), (25), (23) and (26), respectively. Then these matrices can be extracted as blocks from A⁽¹⁾ and A⁽²⁾ in the following way: (46) where i_U is the set of indices for points on Γ_U and i_C is the set of indices for points on Γ_C.

The discretizations of the operators B_NN, G_NN, B_DD and G_DD can be obtained by replacing these operators with their discrete counterparts in (12), (13), (16) and (17). The discretizations of f_k and g_k are denoted f_k and g_k. From now on in the text we shall refer to equations and recursions and let the context determine whether we mean discretized or continuous versions. Discretized quantities will always appear in boldface.

6.4. Accuracy, stability and speed

To illustrate the intrinsic stability and speed of our solver we run the double-step recursions (31) and (20) until 2k = 10⁶, starting with initial guesses f₀ = f_ref and g₀ = g_ref, which is the reference solution on Γ_U given by (39). The evolution of f_k and g_k are shown in Figure 2. The relative L²-error at step k = 1 is only 2 × 10⁻¹³ for f₁ and 2 × 10⁻¹¹ for g₁, which confirms the high accuracy claimed for our solver. As k increases, the errors grow and this is due to the fact that the spectral radii of B_DD and B_NN are larger than unity. In fact, the largest eigenvalue of both these matrices is approximately 1.00001. Note that, for example, the continuous operator B_DD acts on H^1/2(Γ_U), thus properties such as being non-expansive and self-adjoint are inherited for the discretization of this operator with respect to a discretization of the inner product in H^1/2(Γ_U) and do, therefore, not necessarily hold in the standard L²-setting. The schemes used for the discretization might then not be fully optimal and to correct this we shall introduce certain projections in the next section.

Figure 2. The double-step recursions (31) and (20) are run for 2k = 0, 2, 4, …, 10⁶ with the initial guesses f₀ = 0, f₀ = f_ref, g₀ = 0 and g₀ = g_ref. The symbols ‘○’ and ‘*’ refer to f_k, while ‘⋄’ and ‘+’ refer to g_k.

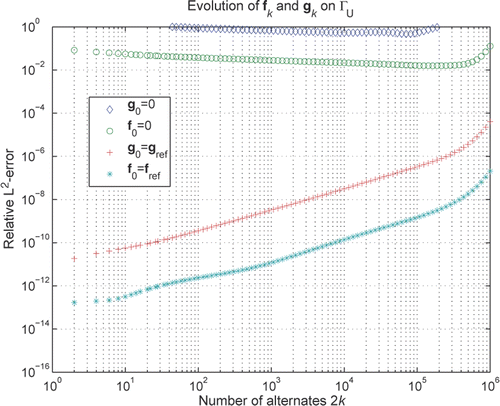
With 50 recursion steps in the construction of the R^(j) matrices, see Section 6 in 21 and in particular the discussion after Equation (44) in 21, the setup time for the matrices of (46) is around 6 s. The time needed to reach 2k = 10⁶ in (20) and (31) is around 5.5 s per initial guess.

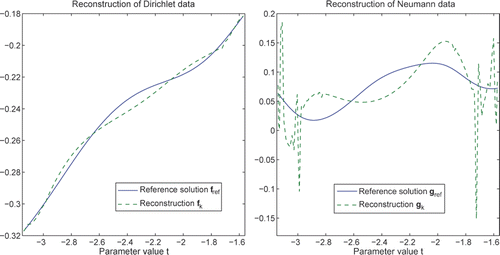
For comparison, Figure 2 also includes results for the initial guesses f₀ = 0 and g₀ = 0. Figure 3 shows f_k and g_k at 2k = 93,260; this is close to an optimal number of steps for both methods.

Figure 3. Reconstruction of the Dirichlet data f_k and Neumann data g_k with the double-step recursions (31) and (20) at 2k = 93,260. The initial guesses are f₀ = 0 and g₀ = 0, respectively.

7. Improved reconstructions from additional information

Cauchy problems are known to be severely ill-posed and thus discretizations of them give rise to matrices that are notoriously ill-conditioned. Note that the spaces in which the data are taken from contain a large class of functions and not necessarily only continuous ones. The reconstructions of Figure 3 are far from satisfactory, but may very well be the best one can get under such general assumptions. At least this holds in terms of accuracy. For improved speed one can rewrite (31) as (47) where (48) and compute f_k, for any k, essentially by evaluating the single N_U × N_U matrix power . The results produced by the closed multi-step expression (47) are surprisingly similar to those produced by the double-step recursion (31). In fact, for the evolution of f_k in Figure 2 and for both f₀ = 0 and f₀ = f_ref, the relative difference between results produced by (31) and (47) is of the order of machine precision for small k and not larger than 10⁻⁸ for large k.

If one has some additional information, besides the Cauchy data, to feed into the solver then this can change the situation completely, also in terms of accuracy. In this section we show how one can achieve much improved reconstructions by supplying such extra information.

7.1. Initial guesses

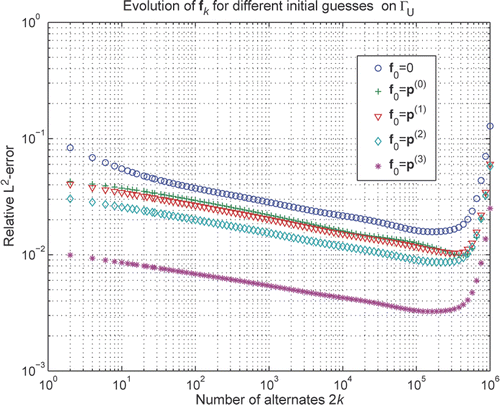
Information about the regularity of u(z) and ∂u(z)/∂ν across the two singular boundary points can be used to construct efficient initial guesses for the alternating schemes. As an example, assume that u(z) and m of its higher order tangential derivatives along Γ are known at the points γ₁ and γ₂. Then one can construct a polynomial p^(m)(t) of degree 2m + 1 in the parameter t on Γ_U, which matches these conditions. Upon discretization this polynomial can then be used as an initial guess for f₀. Figure 4 shows that with p⁽³⁾, which corresponds to the discretization of a matching polynomial of degree seven as initial guess, one can get almost an extra digit for f_k in the double-step recursion (31), compared to using f₀ = 0 as initial guess. The improved reconstruction at 2k = 93,260 shown in Figure 5, also illustrates this, compared with Figure 3.

Figure 4. The double-step recursion (31) is run for 2k = 0, 2, 4, …, 10⁶. The initial guess f₀ is either zero or equal to a discretized matching polynomial p^(m) of degree 2m + 1.

Figure 5. Reconstruction of Dirichlet data f_k and Neumann data g_k+1/2 with the double-step recursion (31) at 2k = 93,260. The initial guess is f₀ = p⁽³⁾. A single recursion step (33) is taken to get from f_k to g_k+1/2.

7.2. Smoothing projections

Information about the regularity of the solution u(z) and the normal derivative ∂u(z)/∂ν on the interior of Γ_U is even more useful. It can be used to restrict the solution space, decrease the number of degrees of freedom, speed up the computations, and increase stability by reducing the largest eigenvalue of the N_U × N_U matrices B_NN and B_DD. In the example of Figure 1 we know that u(z) and ∂u(z)/∂ν are both smooth and can be well-approximated with low degree polynomials on Γ_U.

To use this smoothness information to improve the approximation, introduce a scaled parameter s = 4t/π + 3, that is s ∈ [−1, 1] on Γ_U, and consider the n monomials s^j, j = 0, …, n − 1. Let s^(j) be the discretization of s^j on Γ_U, and let Q_n be a matrix whose columns form an orthonormal basis for the space spanned by the vectors s^(j). Clearly, Q_n can be obtained by a reduced QR-factorization of a Vandermonde matrix V_n with s^(j) as columns. Now introduce the representation of the vector f_k of length N_U in terms of the vector of length n via (49) Then, for example, the discrete projected counterpart of (31) reads (50) where (51) (52) and where superscript ‘T’ denotes the transpose. 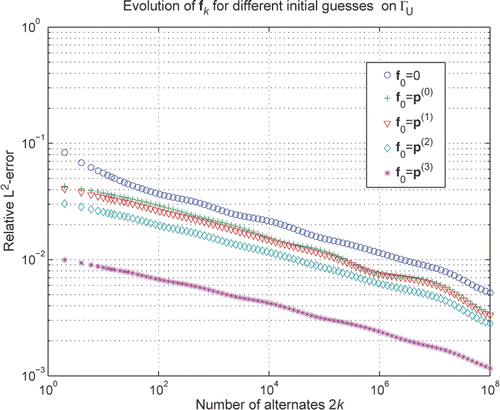The spectral radius of the projected n × n matrix appears to grow monotonically with n, starting at 0 for n = 1. It may be a good idea to choose n as the largest integer which still keeps this spectral radius less than unity. In the example of Figure 1 this corresponds to n ≈ 15.

Figure 6 shows how this projection stabilizes the alternating method; since the projected n × n matrix of (50) is much smaller than the original N_U × N_U matrix B_DD of (31), we can take more recursion steps in a given period of time. With n = 15 the time needed to reach 2k = 10⁸ in the double-step recursion (50) is around 60 s per initial guess.

Figure 6. The projected double-step recursion (50) is run with n = 15 for 2k = 0, 2, 4, …, 10⁸. The initial guess is either zero or equal to a transformed discretized matching polynomial of degree 2m + 1.

7.3. Direct methods

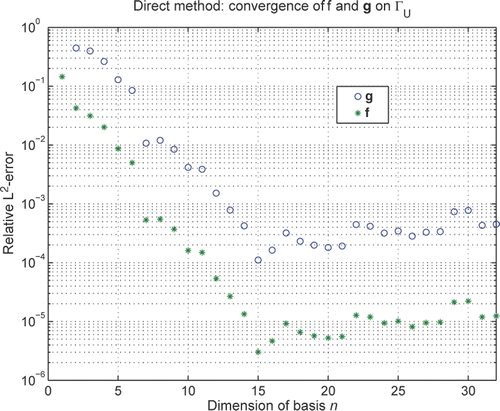
Direct methods may be even more efficient than the alternating schemes in the context of smoothing projections, and especially if n is small. The discrete projected counterpart of (34) reads (53) This n × n linear system can be easily solved with Gaussian elimination and partial pivoting (MATLAB's backslash for square system matrices) in less than a tenth of a millisecond. The solutions produced for f and g via and g = B_NDf + G_NCg_C are rather accurate. The relative L²-error at n = 14, not shown in any figure, is around 2 × 10⁻⁵ for f and around 5 × 10⁻⁴ for g. That is, they are approximately three digits better than the best results obtained by (31) and (20) with f₀ = 0 and g₀ = 0, see Figures 2 and 4.

The highest quality in the reconstruction of f and g from Cauchy data in our example, however, is obtained by the representation of the vector f in terms of a vector and the Vandermonde matrix itself (54) The discrete counterpart of (34) now reads (55) where (56) and c is as in (48). The overdetermined N_U × n linear system (55) is easily solved in the least squares sense with QR-factorization via Householder triangularization (MATLAB's backslash for rectangular system matrices).

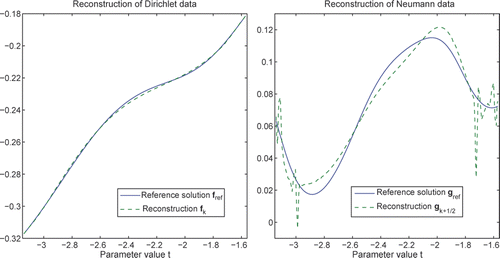
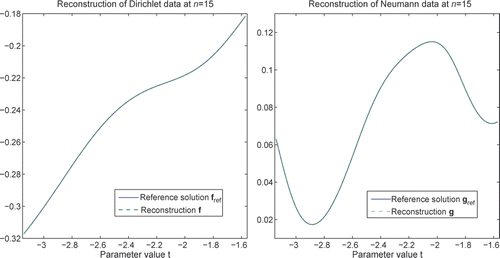
Figure 7 shows the relative L²-errors for the vectors and g = B_NDf + G_NCg_C for various n. The best results are obtained with n = 15, which is in agreement with the prediction of the eigenvalue analysis of Section 7.2. Furthermore, the system matrix of (55) becomes rank deficient in finite precision arithmetic when n = 17, and that too, can be used as a criterion for how large the number n should be chosen. The relative error for f at n = 15 is around 3 × 10⁻⁶ and for g around 10⁻⁴; these are almost four digits better than the best value obtained by (31) and (20) with f₀ = 0 and g₀ = 0, see Figures 2 and 4.

Figure 7. The direct method for f and g via (54), (55) and g = B_NDf + G_NCg_C.

Figure 8 shows f and g at n = 15, and the agreement with the reference solutions is now excellent, compare with Figures 3 and 5.

Figure 8. Reconstruction of the Dirichlet data f and Neumann data g via (54), (55) and g = B_NDf + G_NCg_C at n = 15.

Encouraged by the fast and accurate results produced by the direct method (54) and (55), we also performed an experiment with a more challenging geometry, similar to that of Figure 1, but where the interior domain has the boundary parametrization (57) The number of quadrature panels n_Λ placed on Γ was increased to n_Λ = 84, to ensure full resolution, see Figure 1 in 21 for an illustration, but note that the reference solution (39) is still generated by a single source S₁.

The results produced by (54) and (55) for the geometry of (57), not shown, are similar to those of Figures 7 and 8. Accurate results are again obtained for n ≥ 15, with the smallest relative L²-error for f of around 3 × 10⁻⁴, and for g of around 5 × 10⁻³ at n = 24.

8. Conclusion

We have investigated an implementation of the alternating method 5 using a recent technique 21 based on Fredholm integral equations and Nyström discretization schemes to solve mixed problems for the Laplace equation, for fast and stable numerical reconstruction of harmonic functions from Cauchy data. The Cauchy problem is rewritten as a fixed point equation on the boundary and various direct regularizing techniques for solving this equation have also been investigated. Using the method in 21, it was shown that it is possible to perform millions of iterations with the alternating method in only a few seconds on an ordinary computer. It was also demonstrated how additional information about the smoothness of the data can be incorporated into the procedure to obtain very fast and accurate approximations of both the function and its normal derivative. Future work involves employing these ideas to equations of elasticity and to use other function spaces for further improvement of the performance of the methods, and finally to also consider conjugate gradient schemes like those of 24,25.

Acknowledgements

The first author was supported by the Swedish Research Council under the contract 621-2007-6234.