Identifying intrinsic variability in multivariate systems through linearized inverse methods

Abstract

A growing number of industrial risk studies include probabilistic treatment of the numerous sources of uncertainties. In the uncertainty treatment framework considered in this article, the intrinsic input variability is modelled by a multivariate probability distribution, though only outputs of the physical model may be observed. The objective is to identify a probability distribution, the dispersion of which is independent of the sample size since intrinsic variability is at stake. In order to limit to a reasonable level, the number of (usually large CPU-consuming) physical model runs inside the inverse algorithms, and the linearized Gaussian framework is investigated within this article. First, a simple criterion is exhibited to ensure the identifiability of the model. Then, the inverse problem is re-interpreted as a statistical estimation problem with missing data structure. Hence, EM-type algorithms may be tested, and the expectation-conditional maximization either variant evidences advantages in overcoming the possible pathology of slow convergence which affects the standard EM algorithm. The estimation quality, as suggested through a ratio of epistemic uncertainty to intrinsic variability, proves to be closely linked to classical sensitivity indices. Numerical experiments on simulated and real data sets in nuclear thermal hydraulics highlight the good performances of these algorithms, provided an adequate parametrization with respect to identifiability.

Keywords:

• uncertainty modelling
• intrinsic variability
• linear approximation
• identifiability
• EM and ECME algorithms

1. Introduction

Probabilistic uncertainty treatment is gaining fast growing interest in the industrial field (as reviewed by de Rocquigny et al. 1). In the energy sector, such uncertainty analyses are, for instance, carried out in environmental studies (flood protection, effluent control, etc.), or in nuclear safety studies involving large scientific computing (thermo-hydraulics, mechanics, neutronics, etc.). Besides the uncertainty propagation challenges when dealing with complex and high CPU-time demanding physical models, one of the key issues regards the quantification of the sources of uncertainties. The problem is to choose reliable statistical models for the input variables such as uncertain physical properties of the materials or industrial process or natural random phenomena (wind, flood, temperature, etc.).

A key difficulty, traditionally encountered at this stage, is linked to the highly-limited sampling information directly available on uncertain input variables. An industrial case-study can largely benefit from two strategies: (a) integrate expert judgement, such as likely bounds on physical intervals or more elaborate probabilistic information or (b) integrate indirect information, such as data on other, more easily observable, parameters that are linkable to the uncertain variable of interest by a physical model. Methods for (b) demand the use of probabilistic inverse methods since the recovery of indirect information generally involves the inversion of a physical model. Roughly speaking, this inversion transforms the information into a virtual sample of the variable of interest, before applying to it standard statistical estimation. This field is acknowledged to have quite a large industrial potential in the context of rapid growth of industrial monitoring and data acquisition systems. Yet, it is mandatory to limit to a reasonable level the number of (usually large CPU-time consuming) physical model runs inside the inverse algorithms.

As in Rocquigny and Cambier 2, this article concentrates on the situation where there is an irreducible uncertainty or variability in the input parameters of a physical model. The risk assessment literature (reviewed, for instance, in Helton and Burmaster 3) proved how important it is to distinguish two types of uncertainty: namely the epistemic (or reducible lack of knowledge) type referring to uncertainty that decreases with the injection of more data modelling or number of runs and the aleatory (or irreducible, intrinsic, variability) type for which there is a variation of the true characteristics that may not be reduced by the increase of data or knowledge. In that perspective, classical data assimilation or parameter identification techniques involve the estimation of input parameters (or initial conditions, e.g. in meteorology, cf. Talagrand 4) that are unknown but physically fixed; this is naturally accompanied by estimation uncertainty for which an epistemic variance may be computed, in the sense that it will decrease with the injection of larger observation samples. This is not satisfactory in the cases which motivated the present research, whereby fluid mechanical systems do evidence intrinsically variable input. Input values not only suffer from lack of knowledge, but they also physically vary from one experience to another in the cases of flow observations taken at various times of the year on a fluctuating riverbed, or turbulent fluid flow measurements in a nuclear reactor with changing heat exchange properties. In those cases, the size of observation samples should impact the estimation accuracy, but it should not reduce the variance of the physical fluctuations.

Mathematically, observations are modelled with a vector of physical variables y that are connected to uncertain inputs x through a deterministic (and supposedly quite well-known) physical model y = H(x, d). As a clear difference to classical parameter identification x is not supposed to have a fixed, albeit unknown physical value: it will be modelled a random variable taking different realizations for each observation. The purpose of the algorithm will be to estimate its probability distribution function instead of its point value. On the other hand, d stands for fixed inputs that may represent (i) variables under full control (e.g. experimental conditions) or (ii) uncertainties affecting some model inputs that are considered to be negligible or of secondary importance.

More specifically, the following model is considered: (1) where

•	(Yi) in ℝp denotes the data vectors,
•	H denotes a known function from ℝq to ℝp,
•	(Xi) in ℝq1 denotes non-observed random data, assumed to be independent and identically distributed (i.i.d.) and with distribution 𝒩(m, C),
•	(di) denotes fixed observed variables, with dimension q2,
•	(Ui) denotes measurement-model errors, assumed i.i.d. with distribution 𝒩(0, R), R being known. Variables (Xi) and (Ui) are assumed to be independent.

The aim is to estimate the parameter θ = (m, C).

Before entering the technical part of this problem, a few remarks are to be highlighted.

Two different interpretations follow according to the status given to the random vector. In a first interpretation – which is the one adopted in this article – the distribution of U_i is supposed to be known, representing, for instance, a sensor measurement error deviating from an assumed reliable model. In a second interpretation, the distribution of U_i has to be calibrated to represent the unknown measurement model error, for instance, because the model is less reliable, and may deviate from data for other reasons than sensor fluctuations. Hence R has to be estimated as well.

As already mentioned, the present framework differs from data assimilation, as presented, for instance, in Talagrand 4, in the fact that the uncertain parameters are intrinsically considered as stochastic. In data assimilation algorithms (BLUE, 3dVar, 4dVar, Kalman-filters, etc.), the dispersion of X tends to zero when the sample size n tends to infinity, as discussed in Rocquigny and Cambier 2: the probability distribution obtained via these algorithms quantifies the lack of knowledge and not an intrinsically random behaviour.

Several difficulties may appear. One issue is the identifiability of the parameters of the random variables (X_i), which can be out of reach if the available information is not rich enough (e.g. because the non-observable variables dimension is larger than the dimension of the observed outputs). Another issue is the time needed to compute the physical function H, since H is often the result of a complex code.

A possible answer, used in the following, is to linearize the model around a fixed value x₀. The considered model becomes (2) where J_H(x₀, d_i) is the Jacobian matrix of the function H in x₀, with dimension p × q₁.

As a starting point, choosing the linearization point x₀ at the expert best-estimate value is the natural choice and leads to acceptable results provided that the resulting bias in fixing such expectation remains small compared to the scale of potential non-linearities. While not tested herein, a more advanced process could further involve an adaptive linearization through the fixing of a new x₀ through bias correction.

This method has some drawbacks associated to the approximation error induced and the potential difficulty in choosing an adequate linearization point before identification. Yet, provided that the expert have some reasonable knowledge about proper best estimates for the linearization point (e.g. close to the true expectation of the inputs), its big advantage is to reduce the computational cost to a minimum. Indeed, it requires the running of the potentially CPU-demanding model only for one run at the linearization point if the gradient is available, plus about q₁ to 3q₁ additional runs to estimate finite differences if the gradient is not available.

The remaining part of this article will concentrate on the linearized model. Moreover, both intrinsic variability and model measurement error will be assumed (namely X_i and U_i, i = 1, …, n), independent and identically distributed Gaussian vectors.

The data (X_i) being non-observed, the estimation problem is a missing data structure problem that can be solved with an EM-type algorithm. The EM algorithm was developed by Dempster et al. 5 and is an iterative algorithm with two steps: E-step (for Expectation) and M-step (for Maximization). An extension to this algorithm, called Expectation-Conditional Maximization Either (ECME) algorithm, was proposed by Liu and Rubin 6. This algorithm which can be expected to converge more rapidly than EM has also been employed in the present study. For model (2), the ECME algorithm has been proposed independently by De Crecy 7 under the name ‘Circe Method’.

This article is organized as follows. In Section 2, a criterion is proposed to ensure the identifiability of the linear model (2). In Section 3, the EM and ECME algorithms are described and compared to estimate the linear model at hand. In Section 4, the two algorithms are applied to two examples: The first example consists of simulated data obtained from a quite simplified flooding model and the second example is a real case thermo-hydraulics study carried out in Électricité De France (EDF). A brief discussion ends this article.

2. Identifiability of the model

In this section a criterion is proposed to ensure the identifiability of the linear model (2), rewritten here in a simplified form: where J_i = J_H(x₀, d_i). Further notation is introduced: Hence, Y has dimension np, while J, Γ, C and R are matrix with respective dimensions np × q, np × nq, nq × nq and np × np. Since U_i and X_i are i.i.d. Gaussian vectors, Y is a Gaussian vector with E(Y) = Jm and Var(Y) = ΓCΓ^T + R.

The identifiability of our probabilistic model means that, in addition to the well-known uniqueness of the deterministic identification problem, two different input probability distributions lead to two different output probability distributions.

Hence the studied model is identifiable if and only if for all (m₁, m₂) and (C₁, C₂) or equivalently if and only if for all (m₁, m₂) and (C₁, C₂) (3)

This is equivalent to the injectivity of J, i.e. q ≤ np and rank(J) = q.

Proof of this simple but essential property is a matter of simple linear algebra. The upper line of condition (3) is the definition of the injectivity of J as a matrix, so that injectivity is a necessary condition. Conversely, assuming that J is injective, then J(m₁ − m₂) = 0 implies m₁ = m₂ whatever may be the value of m₁ and m₂. Additionally, suppose Γ(C₁ − C₂)Γ^T = 0, then Γ^TΓ(C₁ − C₂)Γ^TΓ = 0. This implies that C₁ = C₂ if Γ^TΓ is also injective, and indeed a classical linear algebra result shows that the injectivity of J ensures that of Γ^TΓ = J^TJ.

Intuitively, identifiability first requires that there are more observations than parameters, but this is not sufficient. Additionally, it is necessary that each observable component (of vector Y_i) responds in manner that are distinct enough (linearly independent in fact) to a variation of each input component (of vector X_i) in order to be able to distinguish between them.

This identifiability condition provides an easy criterion to check at the very beginning of the study if the inverse problem at hand has a solution. Practically, if the model is not identifiable, several solutions can be envisaged, all based on the use of expert or engineering judgement. If expert knowledge is rich enough, a first solution – that will be illustrated in the flooding example – consists of fixing some of the parameters of the probability distribution of the random variables X; this may be tedious, especially when the parameter to be fixed are standard deviations, generally far more difficult to evaluate a priori than mean values. A simpler approach – illustrated in the real-case thermo-hydraulics example – is to assume that some of the Xs are fixed (equal to a mean value determined by experts), thus neglecting their stochastic nature. But as we will see, this simplification has a price: it can lead to the overestimation of standard deviations for the remaining parameters.

Remark (Empirical Identifiability)

In practice, the condition q ≤ np to get identifiability is not sufficient to ensure that enough data is available for estimation. Consider that q = p = 1; at least np = 2 observations are necessary in order to be able to estimate m and C. With np = 1 observation, only the mean can be estimated. Hence, in the Gaussian case practically, a supplementary condition could be added to ensure that the estimation is feasible. For example n₀q ≤ np, with n₀ greater than 2.

3. EM and ECME algorithms

In the context of missing data, an estimation method largely acknowledged as relevant is the EM algorithm Dempster et al. [5], which is an iterative algorithm with two steps: E-step (Expectation) and M-step (Maximization). An extension devoted to accelerate the EM algorithm, which is known to often encounter slow convergence situations, is the ECME algorithm of Liu and Rubin 6.

In this article, the focus is on the linearized model (2) where J_H(x₀, d_i) is the Jacobian matrix of H in x₀, with dimension p × q₁.

The following notation is used: , i = 1, …, n, denotes the completed data. We denote h_i = H(x₀, d_i); J_i = J_H(x₀, d_i), and consequently Y_i = h_i + J_i(X_i − x₀) + U_i. Moreover, we denote A_i = Y_i − h_i − J_i(m − x₀); ; .

Some preliminary results are useful to define the EM and ECME algorithms for model (2):

•	The variable Yi is a linear combination of Gaussian variables with mean and variance
•	Zi is a Gaussian vector with
•	Xi|Yi is also a Gaussian vector (using a theorem on conditional distributions of a Gaussian vector, see, for instance, 8, p. 35]) with (4) (5)

3.1. EM algorithm

At iteration k + 1, the EM algorithm is composed of two steps:

•	The E-step (Expectation): It consists of computing Q(θ, θ(k)) = E[L(θ, Z)|Y, θ(k)] where L is the completed log-likelihood.
•	The M-step (Maximization): θ(k+1) is obtained by maximizing the function Q, .

The following equations describe more precizely the EM algorithm in the particular case of model (2). Further, the following notation is used: where m^(k) and C^(k) are the value of m and C at iteration k of the EM algorithm.

Then, analytical equations can be derived to compute m^(k+1) and C^(k+1) with respect to m^(k) and C^(k).

Proposition 1

The updating equations for the parameter (m, C) of model (2) at the M step of the EM algorithm are

Proof

See Appendix B.

3.2. ECME algorithm

The ECME of Liu and Rubin 6 is an extension of the ECM algorithm Meng and Rubin 9. The ECM algorithm decomposes the M-step of EM in several CM-steps (Conditional Maximization) maximizing the conditional expectation of the complete-data log-likelihood (conditional on some of the parameters). In the ECME algorithm, some of the CM-steps are replaced by steps maximizing the corresponding constrained actual (incomplete-data) log-likelihood, ln L(θ), instead of the Q-function. This algorithm is expected to be dramatically faster than the EM and ECM algorithms in terms of the number of iterations required for convergence when EM is jeopardized with slow convergence.

More precizely, for model (2), the iteration (k + 1) is expressed as follows. The E-step is the same as in EM and the CM-step of ECM algorithm is replaced by two steps. The first CM-step is as the M-step of EM with m fixed to m^(k). The second CM-step maximizes the incomplete-data log-likelihood over m, assuming C = C^(k+1). According to Liu and Rubin 6, the ECME algorithm monotonically increases the likelihood function, as the EM algorithm does, L(θ): L(θ^(k+1)) ≥ L(θ^(k)); and under some assumptions it reliably converges to a maximum likelihood estimate.

Proposition 2

The ECME algorithm for model (2) leads to the following updating equations:

Proof

See Appendix C.

Remarks

•	Identifiability problems can lead to a singular matrix (see the flooding model example of Section 4.1).
•	Since EM and sometimes ECME algorithms can encounter slow convergence situations, we avoided to use threshold on the likelihood function to assess convergence. On the studied examples, the EM and ECME algorithms are stopped when a large iterations number, nbiter, is reached. The values of nbiter are chosen on an empirical ground for each example.

4. Applications

In this section, the EM and ECME algorithms are applied on two examples: the first example concerns simulated data from a flooding model and the second example involves thermal hydraulic flow within a pressurized water nuclear reactor, with experimental flow measurements.

4.1. Illustration on a flooding model

The model is related to the risk of dyke overflow during a flooding. The available model computes the water level at the dyke position (Z_c) and the speed of the river V with respect to the observed flow of the river upstream of the dyke (Q), and several non-observed quantities: the river bed level beyond upstream (Z_m) and at the dyke position (Z_v), and the value of Strickler coefficient K_s measuring the friction of the river bed, which is assumed to be homogeneous in this quite simplified model. Thus where the values of the section length L and its width B are given and assumed to be fixed (L = 5000, B = 300). U is a centred Gaussian variable with a diagonal variance matrix and standard deviation 0.2 m and 0.2 m s⁻¹.

The linearization point x₀ is chosen equal to the true expectation of (Z_m, Z_v, K_s), i.e. x₀ = (55, 50, 30).

The data have been simulated according to a protocol described in 10, assuming that (Z_m, Z_v, K_s) is a Gaussian vector

In this example, there is clearly an identifiability issue since columns 1 and 3 of the Jacobian J_H of H are linearly dependent (cf. Section 2).

In a first time, to try to solve the identifiability problem, the mean parameter m_Ks is fixed equal to 30 according to the expert judgement. Identifiability problems may be practically detected through the observation of large estimation error as evidenced in the fluctuation of the results of repeated identification. In order to control it, consider the normalized error coefficient (NEC) obtained through the ratio s_θj/σ_j of the standard deviation s_θj of the estimate of parameter θ_j characterizing the jth input (namely its mean m_j or standard deviation σ_j) to σ_j, the intrinsic standard deviation of X_j. We have and In other words, NEC measures the ratio of epistemic uncertainty to intrinsic variability, which should remain small in an efficient identification process which does not pollute the true input variability too much that needs to be estimated by an estimation error. Under identifiability, NEC should tend to zero with limitless data. On the contrary, non-identifiable settings lead to high NEC (see Celeux et al. 11). Roughly speaking, it means that the estimation algorithm is unable to differentiate the role of these physical parameters, and that the response of the algorithm among the infinite set of equivalent solutions is mainly driven by the starting point.

When specifically considering the estimation of mean parameters, another interpretation may be made of the estimation quality, as measured by NEC(m_j), in close relation to the relative importance of the jth input component. As the estimation is undertaken under maximal likelihood, the estimation variance may be approximated from the Fisher information matrix computed at accessible through closed-form differentiation of the Gaussian log-likelihood.

Assuming that the non-diagonal terms can be neglected, it leads to the sensibility indices (column SI in Table 3) (See Celeux et al. 11): where and and and are the variance estimates for . Hence which means that the estimation quality grows not only with n but also with the sensitivity index SI of the jth input which is, in the linear Gaussian case, the relative contribution to output variance explained by the jth input uncertainty. This rather intuitive result proves quite useful in order to control the process, e.g. through prior sensitivity analysis.

Finally, the parameters relative to K_s, m_Ks and σ_Ks, are fixed at the true values – which would require, in practice, a deep and tedious analysis by the experts – while the parameters relative to Z_m and Z_v are estimated through the EM and ECME algorithms with nb_iter = 100. Results from 25 random initial positions are summarized in Tables 1 and 2. NECs values indicate that identifiability is not an issue anymore; as a side effect, it can be seen that the parameter σ_Zv is now better estimated. The advanced expert knowledge is allowed to obtain a robust solution to the inverse problem; however, such a reliable expert judgement on a probability distribution (and not only its mean) is often difficult to get. Now NEC values are smaller with ECME: this comes from the slower convergence of EM, which results in a dependency on the starting point.

Table 1. Parameters estimates for the flooding model via EM, from 25 random initial positions, with fixed m_Ks = 30 and σ_Ks = 7.5.

		Max likelihood	Mean	Standard
Parameters	True values	estimates	estimates	deviation	NEC
mZm	55	55.2110	55.2419	0.1432	0.3098
mZv	50	50.0786	50.0827	0.0196	0.0432
σZm		0.5995	0.4622	0.1063	0.2230
σZv		0.4610	0.4530	0.0079	0.0175

Table 2. Parameters estimates for the flooding model via ECME, from 25 random initial positions, with fixed m_Ks = 30 and σ_Ks = 7.5.

		Max likelihood	Mean	Standard
Parameters	True values	estimates	estimates	deviation	NEC
mZm	55	55.2117	55.2128	6.7859e-04	0.0015
mZv	50	50.0788	50.0787	3.5020e-05	7.7290e-05
σZm		0.5978	0.4619	0.1063	0.2302
σZv		0.4608	0.4531	0.0079	0.0174

Table 3. Estimates, NEC and Sensibility indices (SI) for the mean vector with the ECME algorithm, for the thermo-hydraulics model.

Parameters	Estimates	NEC	SI
m1	0.0670	0.4452	0.1193
m2	0.8736	1.0402	0.0662
m3	−0.8432	0.5334	0.1118
m5	−0.1186	3.2669	0.0754
m8	0.5123	0.6086	0.0883
m9	0.3313	3.1854	0.2908
m10	−0.0005	9.8094	0.2627

4.2. Illustration on a thermo-hydraulics case study

The dataset studied in this paragraph comes from experiments carried out by EDF/R&D between 1990 and 1991 to study the redistributions of diphasic flows. The aim is to evaluate the capacity of a thermo-hydraulics physical model, named THYC, to assess void fractions in a beam of tubes.

The following elements are available:

•	Experimental results (Yi)1≤i≤n (void fractions measurements) are obtained for different thermo-hydraulics conditions (e.g. flows) and coordinates, these experimental conditions are denoted by (di); the experiments are considered as independent,
•	the standard deviation of the measurement errors (Ui)1≤i≤n,
•	the void fractions (H(x0, di))1≤i≤n, computed by THYC for the different experimental conditions (di), the uncertain input variables of THYC being fixed at ‘best estimate’ values x0 = 0,
•	the Jacobian matrices (JH(x0, di))1≤i≤n, which gather the partial derivatives of THYC's outputs with respect to the uncertain input variables.

Hence, the studied inverse problem is characterized by the equation where:

	(Yi): Scalar value (void fraction measurement),
	(Xi): Non-observed data vector of dimension ℝ11, assumed i.i.d. with a Gaussian distribution 𝒩(m, C),
	(di): Deterministic variables, with dimension q2,
	H: Function from ℝq to ℝ (q = 11 + q2),
	(Ui): Measurement errors assumed i.i.d. with a Gaussian distribution 𝒩(0, R), with R = 9×10−4.

The linearized model is Y_i = H(x₀, d_i) + J_H(x₀, d_i)(X_i − x₀) + U_i, 1 ≤ i ≤ n. The aim is to estimate the mean parameter m and the variance matrix C.

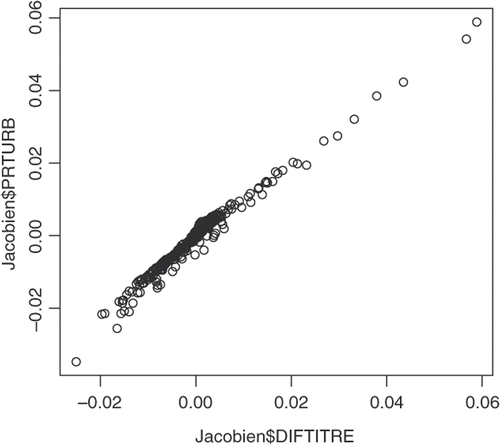
For first time, to ensure the model identifiability, the Jacobian matrix J_H has been studied as recommended in Section 2. Its determinant is actually quite close to zero. This means that identifiability is here an issue. Unlike the previous example, ECME provides results and a misleading appearance of convergence. But the results are littered with numerical inversion problems. Almost linear variables have then been identified from graphical analyses (see, e.g. Figure 1). Hence seven variables have been kept (number 1, 2, 3, 5, 8, 9, 10). For the other variables (numbers 4, 6, 7, 11), the approach used to overcome non-identifiability is different from that described in the flooding example. Indeed, it has been judged too difficult to fix arbitrarily relevant values of their standard deviations; these parameters have therefore been fixed at their best estimated values, thus neglecting their stochastic nature.

In Table 3 the estimates are given for the mean vector m, using the ECME algorithm, with nb_iter = 5000 and the same initial values. We have (see 11 for more details). This means that EM has not yet converged despite the large number of iterations. In this example, ECME fulfills its original goal: it outperforms EM in terms of convergence speed. Finally, it is worth noticing that the indices NEC and SI have the same interpretation. This analogous behaviour of both indices has also been observed for the flooding example (results not reported here and detailed in 11).

5. Discussion and conclusion

Identifying intrinsic variability of physical systems through probabilistic inversion is an important recipe for probabilistic uncertainty studies. Linearization is an attractive option when dealing with high-CPU physical models, as the number of calls is limited to those needed to estimate the Jacobian matrix, hence enabling for the numerically-cheap use of iterative algorithms to perform the probabilistic identification. Once the system is linearized and the input variability may be acceptably modelled by a multivariate Gaussian, the identification was viewed as a statistical estimation problem with a missing data structure.

Provided the fulfillment of a criterion for identifiability, the identification can be undertaken efficiently with two algorithms of the EM family fitting such a statistical structure: two variants, standard EM and ECME, were applied to the estimation problem and illustrated on two physical examples presented in Section 4. In both examples, the ECME algorithm appears to outperform the EM algorithm in terms of convergence speed (all the more so for the thermo-hydraulics example) and seems therefore sensible to solve the inverse problem at hand. However, the choice of the stopping criterion of the algorithm should be considered cautiously: slow convergence may sometimes affect ECME and give a misleading impression of convergence, even if it is less critical than for EM. And in any case, the use of this algorithm should always be preceded, in practice, by an analysis of the identifiability issue which was shown to be rather simple to detect and resolve. Obviously, the relevancy of these algorithms is intrinsically tied to that of the main assumptions, namely a linear approximation and Gaussian distributions. If at least one of these assumptions appears irrelevant, then the estimation problem will require further research. First, linearization could be considered with non-Gaussian distributions such as Weibull or extreme value distributions and still be amenable to maximal likelihood estimation while not requiring more calls to the physical models than the Gaussian case. In order to tackle the non-linearized statistical model (1) with a controlled number of runs of the physical model, several approaches are currently studied. For small input dimensions, de Rocquigny and Cambier 2 suggested a non-parametric algorithm. For larger multivariate systems, further research could include coupling a stochastic version of the EM algorithm with Monte-Carlo Markov Chains tools, or using an Importance Sampling procedure to approximate properly the likelihood. Even in those non-linear cases, linearization could help overcome the potential difficulties and tune efficiently the non-linear methods (choice of a starting point for complex stochastic algorithms, selection of variables to get an identifiable model, etc.), as should be studied further.

Figure 1. The values of the gradient of the H function for the variables six in function of the variable ten.

Acknowledgements

The authors would like to thank Agnès de Crecy (CEA) and Franck Maurel (EDF/R&D) for their support, comments and suggestions.

Appendix

It is assumed that the vector Z can be written Z = (X, Y) where X is the non-observed data vector and Y is observed. It is assumed that the density of Z can be written as where λ = λ(θ) is the vector of parameters called canonical parameter, t(Z) being the corresponding sufficient statistic and a(λ), b(z) real functions.

The E-step of the EM algorithm consists of computing Q(θ, θ^(k)) = E[L(θ, Z)|Y, θ^(k)] where L is the completed log-likelihood.

Using the canonical parameter λ, we can write with and p(x|Y, λ = λ^(k)) the density of non-observed data X conditionally to the observed data Y and the current value of parameter λ^(k).

Then .

The E-step consists of computing the conditional expectation of t(Z) conditionally to the observed data Y and the current value of the parameter λ = λ^(k).

The M-step consists of computing . Solving , λ^(k+1) satisfied (6)

The density of the complete data can be written as and This distribution belongs to the exponential family of distributions, and the EM algorithm described in Appendix A for the exponential family can be used. Considering the canonical parameter λ^T = (λ₁, λ₂) = (C⁻¹m, C⁻¹) leads to The sufficient statistic for λ is .

At (k + 1) iteration, the E-step of EM consists of computing E [t(X)|Y, θ^(k)] where θ^(k) = (m^(k), C^(k)).

We have According to (4), it leads to The M-step of the EM algorithm consists of updating the sufficient statistic t(X). From Equation (A1), it results in where .

Using the derivation of matrix and vector formula, we get The iteration (k + 1) of the EM algorithm is thus

The E-step is the same as in EM and consists of computing the expected completed data sufficient statistic. Denoting δ_i = X_i − m, we have Y_i = h_i + J_i(δ_i + m − x₀) + U_i and The matrix is the sufficient statistic for the canonical parameter λ = C⁻¹. In this case, the function a of the exponential family distribution is . Thus, at iteration (k + 1), the E-step consists of computing the term E[t(δ)|Y, m^(k), C^(k)]. According to (4) and (5), it leads to from which it is deduced that

CM-step 1 for ECME: (Estimation of the variance C)

Fixing m = m^(k), C^(k+1) is computed to maximize the expected complete-data likelihood for the exponential family distribution at hand (Appendix A). From according to the equality (A1), it leads to

CM-step 2 for ECME: (Estimation of the mean m)

The mean m is updated by maximizing the constraint actual (incomplete-data) log-likelihood with C fixed to C^(k+1). Since Y_i has a Gaussian distribution , the associated log-likelihood is Solving the equation leads to