Detection of anomalies inside hollow metal cylindrical structures

Abstract

The evaluation of the physical conditions of a hollow metal cylindrical structure is critical in many applications, such as those involving oil or power generating industries or water pipeline networks. Direct and internal inspection is often not possible or highly costly in terms of time and inspection tools. We present here a guided waves-based technique whose particularity is to detect and to quantify a circular anomaly inside a hollow metal cylindrical structure, while being deployed. The technique requires only one measurement point to obtain information on remote sections that are hundreds of metres apart. Radar equipment sends an electromagnetic wave through an open end of the structure and it receives the backscattered field, which is produced by variations of the internal hollow structure radius (deformations, welding joints, etc.). We derive the link between the recorded signal, which carries information on amplitude and propagation time, the circular anomalies parameters, defined by the percent radial reduction, r_ap, and the deformation length, l_a, avoiding the complications of the most classification algorithms. The anomaly identification is obtained through an inversion procedure that performs well with both the synthetic and real data. In the latter case, the estimated parameters of a given anomaly ( = 4.9%, = 3.85 m) are in good agreement with the actual ones (r_ap = 5%, l_a = 3 m).

Keywords:

• non-destructive investigation
• circular waveguides
• radar scattering
• time domain reflectometry
• phase constant

AMS Subject Classifications::

• 32A07
• 78A46
• 34M55

1. Introduction

The integrity of a hollow metal cylindrical structure is critical in many applications, i.e. power or oil generating industries or water pipeline networks, where proper inspection and maintenance is a demanding task, utilizing techniques such as direct assessment methods, hydrostatic testing and internal inspection tools. Direct assessment methods imply visual and physical (internal and external) observations; hydrostatic testing involves pressuring the structure to a level equal to or above its normal operating pressure; internal inspections are run with sophisticated technological tools (i.e. robots) that, moving along the structure, detect point-by-point loss of metal and, in some cases, deformations. The operators generally use a combination of direct assessments, internal inspection tools and/or hydrostatic tests for ensuring the integrity of the whole structure 1. In the last few decades, to overcome those difficulties and to save time, various non-destructive techniques were developed, among those based on the wave propagation in hollow cylinders 2, both empty and filled. Published works report on ultrasonic wave analysis to detect and classify defects and deformations 3–10. In another approach, defect classification is based on the identification of the signal features that are sensitive to the defect in the time domain and/or in the frequency domain by using numerical techniques and classification algorithm jointly 11.

We introduce here an indirect method for the evaluation of the physical condition of a metal cylindrical hollow structure by using electromagnetic waves that let us inspect the structure while being deployed up to distances of hundreds of metres. We restrict our study to a structure composed of the elements of known length, welded together, and we are interested in the detection of cylindrical deformations. Radar equipment sends a source signal through an open end of the structure and it receives the backscattered wave. Metal cylindrical axial sections are modelled as dispersive transmission channels. According to the theory of time domain reflectometry (TDR), the electromagnetic propagation along non-uniform transmission lines gives rise to transmission–reflection effects not present in a uniform structure 12. We use these effects to detect and to characterize any possible anomaly. The reflections produced by circular anomalies are unpredictable and their amplitude can be very low, depending on the extension and on the magnitude of the deformation. On the other hand, experimental data show that the joints between the cylindrical elements produce detectable reflections that can be easily modelled. So, instead of looking directly for the reflections from the anomalies, we look for the modifications of the reflections from the joints with respect to the reference (uniform structure) reflections. In fact, a deformation of a cylindrical element modifies the reference electromagnetic propagation constant, which in turn produces a modification in the reference signal transmitted through the element. Indeed, a source could excite all the modes which propagate in the system operating frequency bandwidth. That is why the experimental setup was designed to have the bandwidth of the dominant propagation mode. This let us develop a single mode model as the converted modes, that could possibly result from the discontinuities, are with negligible power compared to the dominant one.

We have studied and realized a simulator that computes the electromagnetic response of a hollow cylindrical structure including a circular anomaly: model parameters are the geometry of the elements and of the deformation. Anomaly detection is performed through an inversion procedure, whose objective is to fit the backscattered signal due to the joints (input) with the simulator output, for varying length and depth of a circular anomaly. We have tuned and optimized the procedure on synthetic data. Then, we have validated the system on real data acquired in a test site under controlled conditions.

Section 2 shows the TDR model. Section 3 describes the modelling of the circular anomaly, i.e. the calculation of the specific phase constant of a deformed metal cylindrical hollow structure, as a function of the circular anomaly parameters. Section 4 describes the inversion procedure, i.e. the estimation of the properties of a circular anomaly inside a hollow metal cylindrical structure. Section 5 shows the detection results on synthetic and real data. Conclusions and perspectives are drawn in Section 6.

2. TDR model

We assume in the following that

1.	the hollow metal cylindrical structure is made up of elements of equal length l and radius r, welded together;
2.	a section of the structure is composed by one or more consecutive elements;
3.	the welded joints produce a reflected signal described by a scalar (reflection coefficient), while their effect on the transmitted signal can be neglected and
4.	a circular anomaly is a constant and abrupt reduction of the internal radius inside one section.

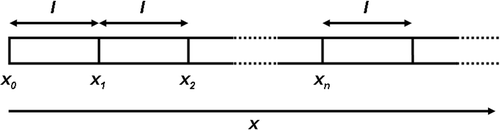
We define a curvilinear axis x along the structure. The opening of the structure is at coordinate x₀. The nth junction is at coordinate x_n (Figure 1). The input signal is a wavelet w(t, x₀), where t is the observation time (s), generated at the open end of the structure. The signal at the distance x_n, s(t, x_n), is given by the convolution of the transmitted wavelet w(t, x₀) with the channel impulse response h(t, x₀ x_n), or in the frequency domain, where f is the frequency (Hz).

Figure 1. Metal cylindrical hollow structure.

The global channel transfer function between the coordinates x₀ and x_n, H(f, x₀, x_n) can be written as follows: with A(f, x₀, x_n) and B(f, x₀, x_n) the corresponding magnitude and phase.

H(f, x₀, x_n) can be factorized in the product of the n transfer functions of the structure elements, where A(f, x_i, x_{i + 1}) and B(f, x_i, x_{i + 1}) are, respectively, the magnitude and the phase of H(f, x_i, x_{i + 1}). Similarly, A(f, x₀, x_n) and B(f, x₀, x_n) can be factorized as follows:

For a generic section between the joints at coordinates x_i and x_j, with x_i < x_j (Figure 2), we have or in the frequency domain,

Figure 2. Section of a metal cylindrical hollow structure.

The magnitude A(f, x_i, x_j) and the phase B(f, x_i, x_j) of H(f, x_i, x_j) are functions of the specific attenuation α(f) (Np m⁻¹) and of the phase constant β(f) (rad m⁻¹), both depending on the frequency 13 (1) (2) with l_s = x_j - x_i the section length.

The transfer function of the section can be estimated by the spectral ratio

A small anomaly in the section mainly affects the phase of the transfer function and we can observe the section integrity by measuring the specific phase constant. In practice, we record the reflections s_obs(t, x_j) and s_obs(t, x_i) (subscript ‘obs’ stands for the observed data) from the joints at positions x_j and x_i, and we compute (3) where the angle symbol ∠ represents phase.

Equation (3) is the key to the anomaly identification, provided we have the relations between the phase constant and the geometrical and electromagnetic parameters of the anomaly. These relations will be derived in the following section.

3. Circular anomaly in a hollow cylindrical structure

We analyse the effects on the electromagnetic propagation parameters of a circular anomaly in a hollow metal cylindrical section modelled as a circular waveguide. The determination of the propagation constant in a circular waveguide surrounded by a medium with infinite conductivity is well known. Here, we are interested in a solution that works: (a) for external medium with finite conductivity; (b) near the cut-off region and (c) with accurate approximation and low computational cost. Hence, the propagation constant is derived from the characteristic equation through a perturbation technique developed expressly. We consider a small anomaly so that only the phase constant β(f) is affected. We briefly remind the main results, while the reader is referred to 14 for details.

3.1. Specific phase constant of metal cylindrical hollow structures

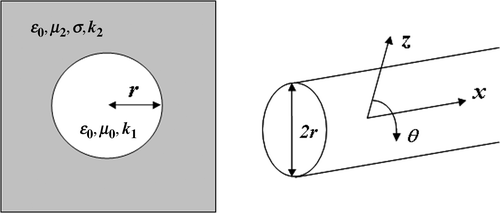
Let us consider a hollow circular cylinder of a radius r and of infinite length, surrounded by a dissipative medium of finite conductivity (Figure 3). k₁ is the propagation constant of the internal medium with permittivity ε₁ = ε₀ and permeability μ₁ = μ₀; k₂ is the propagation constant of the external medium with finite conductivity σ₂, permittivity ε₂ = ε₀ and permeability μ₂ = μ_r2μ₀.

Figure 3. System geometry and cylindrical reference system (z, θ, x).

Under the assumption of single mode model (Section 1) and among the four types of normal modes that occur in such a cylinder, we inspect the hybrid electric mode HE₁₁ which is the dominant one. Its propagation constant γ₁₁ can be calculated by solving the simplified characteristic equation 14 through a perturbation technique to single out the equation's roots

As long as the HE₁₁ mode is of interest, we obtain (4) (5) (6) (7) where ν₁₁ can be approximated as

The phase constant β is the imaginary part of γ₁₁, easily computed by solving Equation (7) (8)

3.2. Model of the anomaly in a cylindrical hollow structure

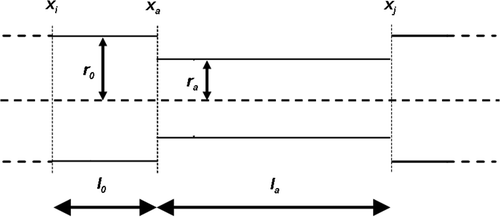
We can divide a deformed section delimited by the joints in position x_i and x_j, in two subsections: a regular one (x_i < x < x_a) and a deformed one (x_a < x < x_j). The coordinate x_a defines the starting position of the anomaly (x_i < x_a < x_j).

The anomaly profile is defined by the percent radial reduction as follows: (9) where r₀ and r_a(x) are the nominal radius of the structure and the reduced one, respectively, that can vary along the x direction.

Since we are looking for the transmission effects, we can approximate the anomaly in a section of the structure as a constant radial reduction (Figure 4).

Figure 4. Circular anomaly as a constant radial reduction.

In this case, the properties of the anomaly are its length (l_a), and the constant percent radial reduction of the deformed subsection (r_ap), so that Equation (9) becomes (10) with r_a the value of the reduced radius.

The global section transfer function H(f, x_i, x_j) can be factorized in the product of the regular and of the deformed subsection transfer functions,

Going to amplitude and phase representation,

We can express A(f, x_i, x_a) and B(f, x_i, x_a) in terms of the specific attenuation α₀(f) (Np m⁻¹) and of the phase constant β₀( f) (rad m⁻¹) of the regular subsection (11) (12) with l₀ = x_a−x_i the regular subsection length.

Similarly, A(f, x_a, x_j) and B(f, x_a, x_j) can be expressed in terms of the specific attenuation α_a(f) (Np m⁻¹) and of the phase constant β_a(f) (rad m⁻¹) of the deformed subsection (13) (14) with l₀ = x_j−x_a the deformed subsection length.

The global section transfer function H(f, x_i, x_j) becomes

From Equations (1), (11) and (13) we obtain (15)

From Equations (2), (12) and (14) we obtain (16)

We want now to relate the phase constant in Equation (16) with the anomaly radius, length and electromagnetic parameters. β₀(f) is computed from Equation (8) by substituting the radius r with the nominal radius of the regular subsection, r₀. Then, using Equations (8) and (10), it is possible to link explicitly the phase constant of the deformed subsection, β_a, to the percent radial reduction, r_ap (17)

Finally, β(f) can be calculated from Equations (16) and (17) as follows: (18)

For the sake of simplicity, we have omitted the frequency dependence of β, β₀, v₁₁ and k₁ in Equation (18).

4. Inversion procedure

The detection procedure iteratively analyses the reflections of the welded joints in order to infer the transmission properties of each structure element.

In the first step, we extract the echoes of the joints delimiting the section during the analysis from the backscattered signal. This task can be achieved by converting the known position of the joints (spatial coordinate) into the two-way travel time domain (time coordinate), using a reference propagation velocity. Then, we compute the spectra of the echoes and, from Equation (3), the phase constant β_obs(f). Finally, we obtain the parameters of the anomaly by inverting Equation (18), in the bandwidth of the signal. The input of the inversion procedure is the observed data β_obs (f) and the outputs are the length l_a of the anomaly and the percent radial reduction r_ap.

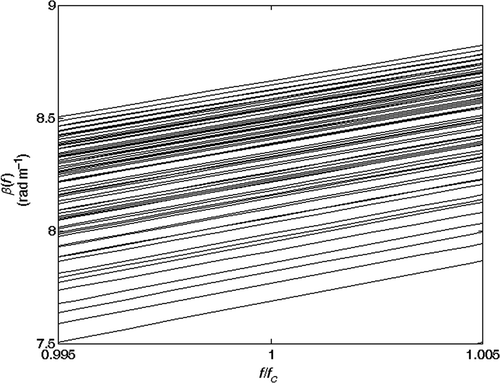
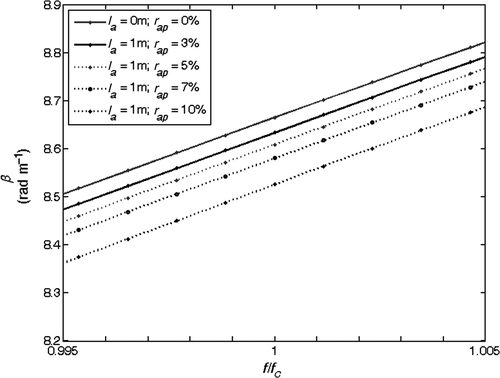
The presence of the product term β_a(f) · l_a in Equation (18) leads to a non-linear inversion. Due to the strong non-linearity of the inverse problem, we estimate the anomaly parameters through an exhaustive search technique. We pre-calculate by means of Equation (18) a look-up table with K different phase curves β_i(f) (i = 1, …, K): each curve corresponds to a pair (l_a, r_ap)_i of the anomaly. Figure 5 shows an example of a lookup-table with different curves β_i(f).

Figure 5. Lookup-table with different curves β_i(f) for different pairs (l_a, r_ap)_i. Note: l_a varies from 0 to 12 m with steps of 1 m; r_ap varies from 0% to 10% with steps of 1%. The curves are not equally spaced and the mapping is strongly non-linear.

The minimization of the L₂ norm of the distance between the observed data β_obs(f) and β_i(f) gives the recalculated data and the estimated model parameters 15. Analytically

In practice, the inversion is applied on a discrete and finite set of frequencies and the inverse problem can be formulated in matricial form.

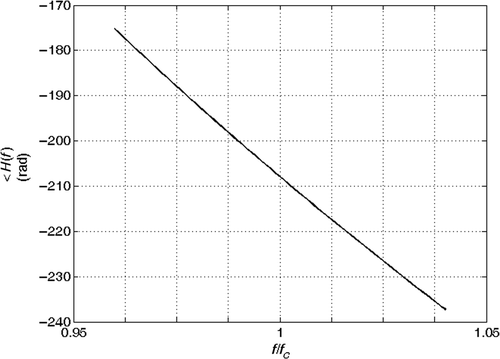
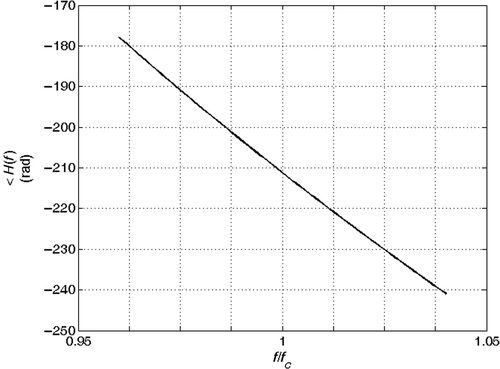
It is interesting to analyse the behaviour of the β_i(f) curves for different values of the section length l_s. Figures 6 and 7 show the curves for l_s = 12 and l_s = 24 m, respectively. We observe that for increasing l_s, there is a compaction of the curves, so that their relative distances decrease: the inversion procedure becomes more sensitive to noise and it could output inaccurate solutions. This suggests us to consider the minimum available section length.

Figure 6. β_i(f) curves as a function of normalized frequency, for some (l_a, r_a)_i pairs. Section length l_s = 12 m.

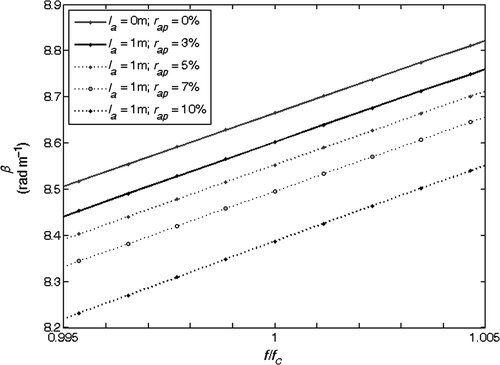
Figure 7. β_i(f) curves as a function of normalized frequency, for some (l_a, r_a)_i pairs. Section length l_s = 24 m.

The solution of this inverse problem is intrinsically not unique as different pairs could give the same β_i(f) curve. The lack of uniqueness has been overcome by pre-computing the lookup-table with a discretization step which ensures that the solutions that differ numerically result in the same physical solution.

5. Examples

The inversion procedure is validated on synthetic and real data.

5.1. Synthetic data

We test the detection procedure on a synthetic data set. We consider a realistic structure composed of elements of length l_s = 12 m, welded together. The section located between the coordinate x_i = 24 and x_j = 36 m has a radial reduction (circular anomaly) for a portion of its total length l_s = 12 m. We consider two cases: (a) the absence of anomaly and (b) the circular anomaly of radial reduction r_ap = 3% and length l_a = 2 m. We simulate the transmission of a typical band-pass signal 16, around a proper carrier frequency, f_c, inside the hollow metal cylindrical structure. We propagate the signal taking into account: the backscattering effects due to the joints, for both cases (a) and (b); the variations in the transfer function of the structure due to the presence of the anomaly to detect, in case (b) only.

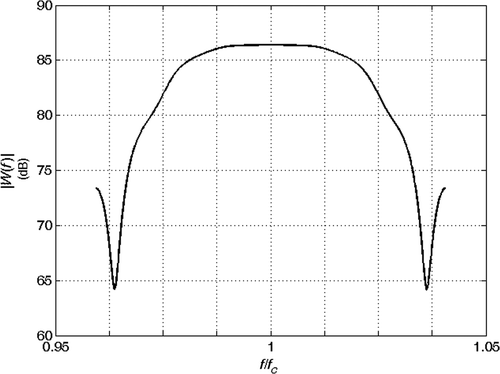
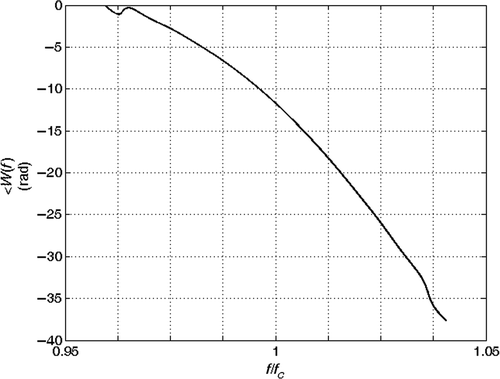
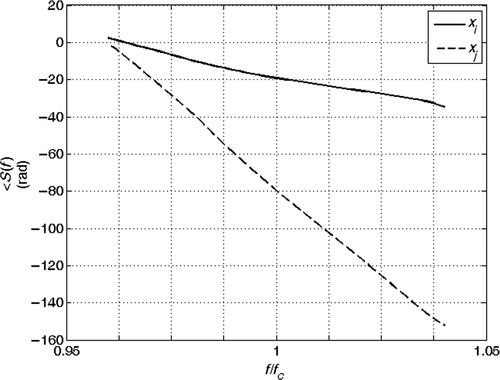
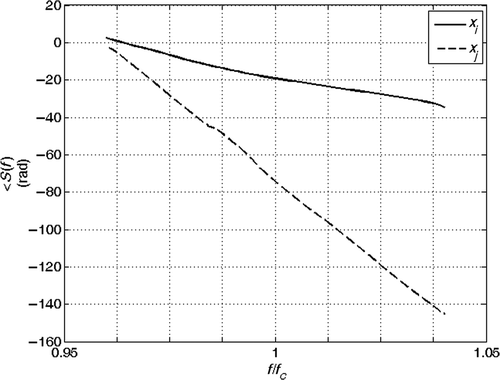
Figure 8 is the absolute value of the transmitted signal at x = 0 m, i.e. before its propagation in the section, as a function of time. Figures 9 and 10 are the magnitude and the phase of the corresponding frequency spectrum.

Figure 8. Absolute value of the transmitted waveform (after demodulation).

Figure 9. Spectrum amplitude of the transmitted signal shown in Figure 8.

Figure 10. Spectrum phase of the transmitted signal shown in Figure 8.

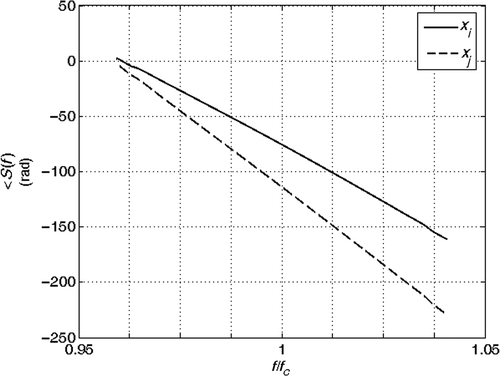
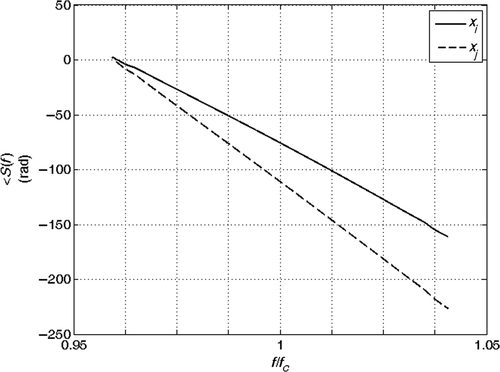
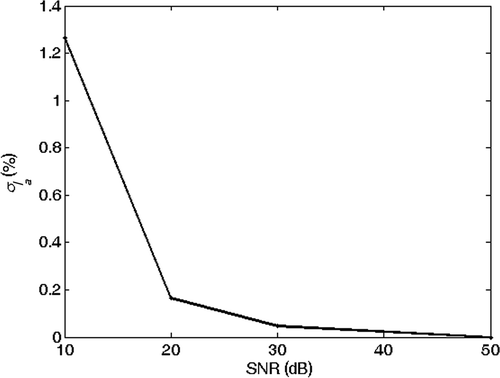
Figures 11 and 12 show the echoes (absolute value) from the joints at coordinates x_i and x_j for the two cases (a) and (b). Here we assume that the echoes of the joints during the analysis do not interfere with the echoes from other joints. This assumption is confirmed also by experimental results. Figures 13 and 14 show the phase of the spectrum of the echoes during the analysis and Figures 15 and 16 are the phase of their ratio, which is proportional to β_obs(f). The solution of the inverse problem is reported in Table 1: in the absence of noise, the estimated model is the exact model. We then performed the inversion of 1000 noisy realizations of the synthetic data of case (b), by adding to the received signal a Gaussian noise with zero mean and increasing variance, corresponding to a SNR changing from 50 to 10 dB. The mean value and the standard deviation (SD) of the inverted results are shown in Figures 17–20 for different SNRs. We think that the anomaly identification is accurate for most application down to SNR ≅ 20 dB.

Figure 11. Absolute value of the echoes from the joints at coordinates x_i and x_j: l_a = 0 m, r_ap = 0%.

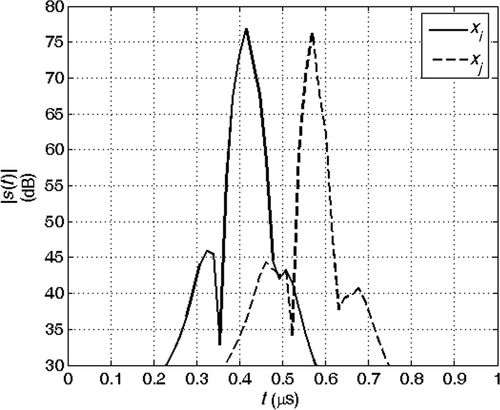
Figure 12. Absolute value of the echoes from the joints at coordinates x_i and x_j: l_a = 2 m, r_ap = 3%.

Figure 13. Spectra phase of the signals in Figure 11.

Figure 14. Spectra phase of the signals in Figure 12.

Figure 15. Phase of the spectra ratio of the joints at coordinates x_i and x_j: l_a = 0 m, r_ap = 0%.

Figure 16. Phase of the spectra ratio of the joints at coordinates x_i and x_j: l_a = 2 m, r_ap = 3%.

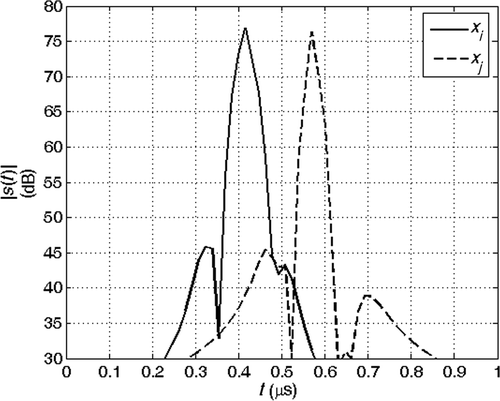
Figure 17. Mean value of the inverted anomaly length versus SNR. Exact solution: l_a = 2 m and r_ap = 3%.

Figure 18. SD of the inverted anomaly length versus SNR. Exact solution: l_a = 2 m and r_ap = 3%.

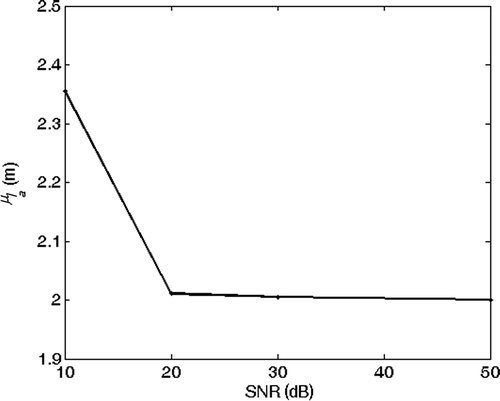
Figure 19. Mean value of the inverted percentage radius reduction versus SNR. Exact solution: l_a = 2 m and r_ap = 3%.

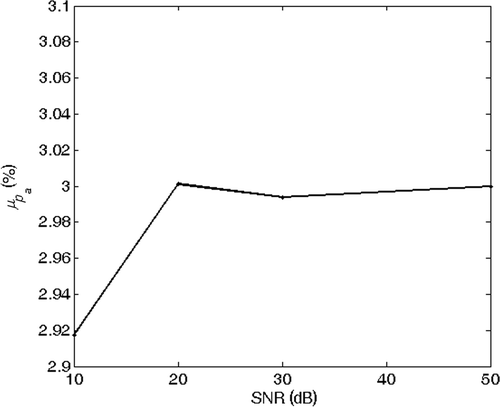
Figure 20. SD of the inverted percentage radius reduction versus SNR. Exact solution: l_a = 2 m and r_ap = 3%.

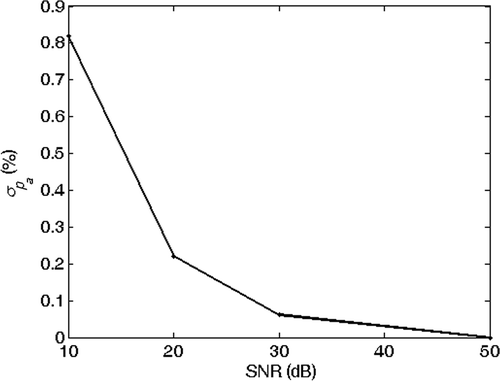
Table 1. Inverted parameters–synthetic data: regular (a) and deformed (b) elements.

Example	la(m)	rap (%)
(a), no noise	0	0	0	0
(b), no noise	2	3	2	3
(b), SNR = 10 dB	2	3	2.3 ± 3.8	2.9 ± 2.5
(b), SNR = 20 dB	2	3	2.0 ± 0.5	3.0 ± 0.7

5.2. Real data

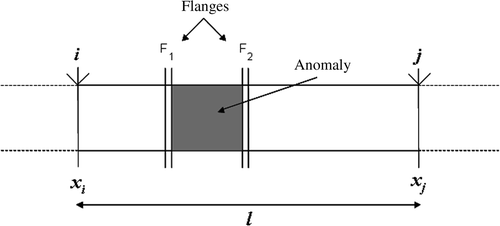
We have acquired a real data set in controlled conditions (known anomaly parameters), in order to validate the inversion algorithm. The hollow metal cylindrical structure is composed of elements of (known) length l ≅12 m, welded together. The section located between the coordinate x_i ≅ 96 m and x_j ≅ 108 m has a radial reduction for a portion of its total length l_s ≅ 12 m. The deformed element is inserted into the section by the means of two screwed flanges at the distances x_F1 ≅ 99 m and x_F2 ≅ 102 m (Figure 21). We report two cases: (a) the absence of anomaly and (b) the circular anomaly of radial reduction r_ap ≅ 5% and deformation length l_a ≅ 3 m.

Figure 21. Experimental setup for the detection of the circular anomaly.

The acquisition system is a quasi-monostatic pulse radar 17–20 equipped with an antenna operating at vertical polarization employed both as transmitter and receiver. Its response is assumed to be constant in the frequency range of interest. Coherent transmission and reception are performed. The input signal is the same one introduced in the synthetic data example (Figures 8–10). In order to increase the SNR, the system returns the mean of a given number (≈10,000) of acquisitions, with fixed geometry and input signal.

Real data are affected by different sources of noise (Figures 22 and 23):

1.	random noise (SNR ≅ 30 dB in the analysed signals);
2.	RF spurious noise signals;
3.	leakage at low frequency and
4.	spurious echoes due to the flanges.

Figure 22. Real data for a regular section. The arrows indicate the starting time of the echoes from the joints.

Figure 23. Real data for a deformed section. The arrows indicate the starting time of the echoes from the joints.

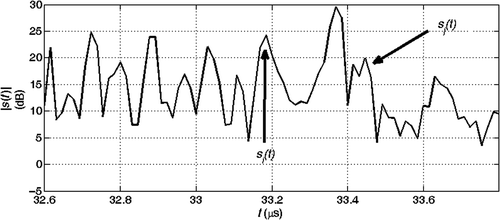
We successfully reduce the effect of the noise by filtering, except for the spurious echoes due to the flanges. These artificial discontinuities (i.e. not present in a structure made of constant length elements) generate backscattered signals that interfere with the echoes from the joints delimiting the section during the analysis.

We propose two approaches in order to lower the effect of the flange reflection noise:

1.	Estimate the echoes of the flanges and then remove them from the recorded data: this solution is complicated by the fact that it is necessary to model the flanges and
2.	Evaluate the phase constant from the reflections of one joint long way before the anomaly and the other past the anomaly, where the flange interference noise is strongly attenuated: this solution increases the condition number associated to the inverse problem.

We find a good compromise by applying both the previous approaches. First, we estimated and removed the echoes due to joints and flanges, thanks to an accurate knowledge of the position of the discontinuities along the structure. Then, since the previous procedure does not completely remove the interfering echoes, we doubled the section length, by considering the reflections from the joints at x_i ≅ 84 m and x_j ≅ 108 m (l_s ≅ 24 m).

Figures 24 and 25 are the extracted echoes (absolute value). Figures 26 and 27 show the phase of the spectrum of the echoes during the analysis and Figures 28 and 29 are the phase of their ratio, which is proportional to β_obs(f). The estimated anomaly parameters are reported in Table 2. The accuracy of the result is interesting for many applications.

Figure 24. Absolute value of the echoes from the joints at coordinates x_i = 84 m and x_j = 108 m: real data with regular section.

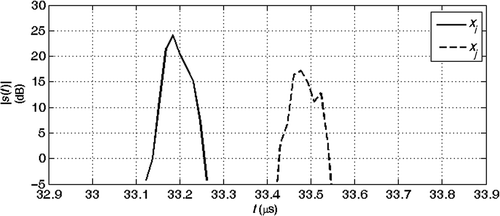
Figure 25. Absolute value of the echoes from the joints at coordinates x_i = 84 m and x_j = 108 m: real data with deformed section.

Figure 26. Spectra phase of the signals in Figure 24.

Figure 27. Spectra phase of the signals in Figure 25.

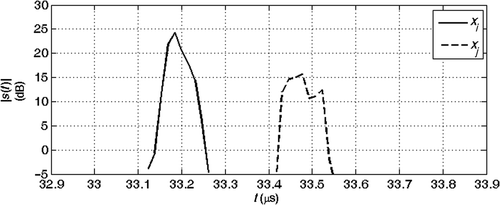
Figure 28. Phase of the spectra ratio of the joints echoes at x_i = 84 m and x_j = 108 m: real data with regular section.

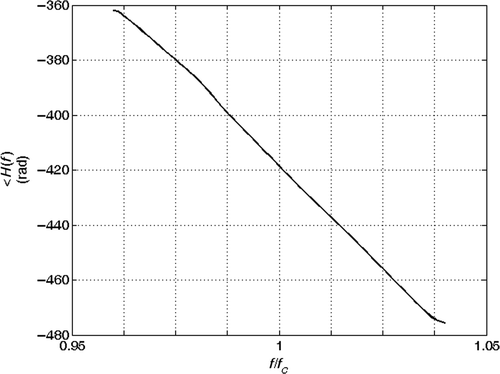
Figure 29. Phase of the spectra ratio of the joints echoes at x_i = 84 m and x_j = 108 m: real data with deformed section.

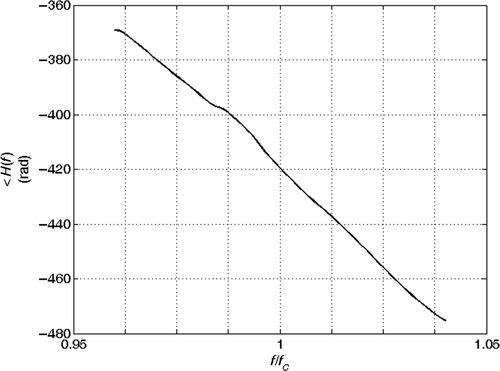
Table 2. Inverted parameters–real data: regular (a) and deformed (b) elements.

Example	la(m)	rap (%)
(a)	0	≅0	0.35	0.35
(b)	≅3	≅5	3.85	4.90

6. Conclusions

We have presented an indirect technique which is able to detect and to quantify circular anomaly parameters inside a hollow metal cylindrical structure. It operates remotely by sending an electromagnetic signal from an open end of the structure and by recording and processing the backscattered signal. The maximum distance of detection is limited by the noise and by the attenuation of the transmission line.

The detection procedure analyses the echoes due to the localized discontinuities along the structure (like the joints, whose position is known), and obtains the geometrical parameters of the crossed sections, by inverting the relation between the signal and the hollow element parameters. The condition number of the inverse problem increases with the distance between the joints, whose backscattered signals are used in the processing.

The precision of the inversion strongly depends on the correct extraction of the reflections from the junctions: this implies an appropriate SNR and a good description of the interference effects. Interfering events could be treated with a ‘section stripping’ approach: the section parameters are estimated and removed in sequence one at a time.

We have tested the procedure on synthetic and real cases, showing that the estimation accuracy can be interesting for many applications.

The inversion procedure presented here is quite general because it is based on the phase difference measurements and it is, therefore, independent from the transmitted signal and from the antennas. Future developments are the inclusion of higher order propagation modes and the extension of the operative frequency range.

Acknowledgements

We thank Adriano Calzavara (Saipem SpA), Antonio Passerini (Saipem SpA) and Roberto Visentin (Saipem Energy Services SpA Div SONSUB) for providing the real data set, for the permission to show these results and for the valuable discussions.