The method of fundamental solutions for the inverse conductivity problem

Abstract

In this article, we propose a simple method for detecting an inclusion Ω₂ embedded in a host electrostatic medium Ω₁ from a single Cauchy pair of voltage and current flux measurements on the exterior boundary of Ω₁. A nonlinear constrained minimization regularized method of fundamental solutions is developed for the numerical solution of this inverse problem. The stability of the numerical scheme is investigated by inverting measurements contaminated by random noise.

Keywords:

• inverse problem
• electrical impedance tomography
• method of fundamental solutions

AMS Subject Classifications::

• Primary 33A65, 65N35
• Secondary 65N22, 65F05, 35J05

1. Introduction

It is well-known (see, e.g. 1), that electrical impedance tomography (EIT) is a non-intrusive technique in which an image of conductivity of the interior of an object is inferred from the surface measurements of electrical quantities. Mathematically, if u denotes the electric potential and n the outward unit normal, given measurements of a pair of (u, ∂_nu) = (voltage, current flux) on the accessible outer boundary ∂Ω₁, we search for an unknown inclusion (anomaly) Ω₂ with conductivity k ≠ 1, representing, say, a tumour, within the conducting host medium Ω₁. Some uniqueness results exist for determining the inclusion Ω₂ in this case, this is a polyhedron or a ball from known single Cauchy data pair measurements 2,3. The problem is still, however, difficult to solve since it is non-linear, ill-posed (unstable) and computationally intensive 4–8. Prior to this study, this transmission problem was investigated using the boundary element method (BEM) and its variants in, for example, 9–12.

Very recently, a new inverse problem algorithm, which uses the method of fundamental solutions (MFS) iteratively for the determination of a perfectly conducting (k = 0) or a perfectly insulated (k = ∞) inclusion, has been proposed in 13 and 14, respectively. The goal of this study is to extend this approach to the more realistic (and difficult) case when 0 < k ≠ 1 < ∞.

This article is organized as follows. The mathematical formulation of the problem is given in Section 2. The MFS and the proposed nonlinear iterative regularization algorithm are described in Section 3. Numerical results are presented in Section 4 and, finally, in Section 5 some conclusions and suggestions for future applications are given.

2. Mathematical formulation

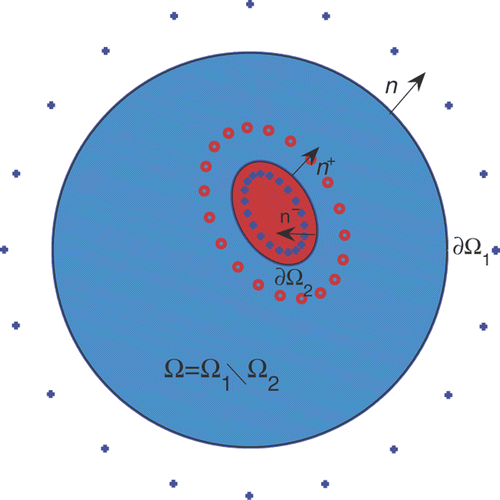
The inverse conductivity problem can be formulated mathematically in the following way. Let Ω₁ be a bounded domain in ℝ^d, d ≥ 2, with a Lipschitz boundary and Ω₂ a subdomain compactly contained in Ω₁, such that Ω ≔ Ω₁\Ω₂ is connected (Figure 1). The refraction (transmission, conjugate) problem for the electrical potential u is given by (1) subject to the Dirichlet boundary condition (2) and to refraction conditions related to the continuity of the voltage u and the current flux densities ∂u/∂n⁻ and k ∂u/∂n⁺ across the interface ∂Ω₂. Here n⁻ and n⁺ are the outward unit normals to the boundaries ∂Ω\∂Ω₁ and ∂Ω₂, respectively. In (2.1a), 𝒳_Ω2 denotes the characteristic function of the domain Ω₂ and f ∈ L²(∂Ω₁) is a given (voltage) function. It is well-known 15, p.197] that the direct problem of finding u ∈ H¹(Ω₁) satisfying (2.1a) and (2.1b), when k and Ω₂ are known, has a unique solution. Assuming that k is known, the inverse conductivity problem requires finding Ω₂ from the knowledge of the Dirichlet-to-Neumann map for finitely many data f ∈ L²(∂Ω₁).

Figure 1. Geometry of the problem. The dots show the location of the singularities in the MFS.

The refraction model under investigation given by Equations (2.1a) and (2.1b), and the corresponding transmission conditions on the interface ∂Ω₂ can be recast in a more convenient form, by defining u = u₁ in Ω and u = u₂ in Ω₂, where u₁ and u₂ satisfy (3) (4) (5) and (6) If we now assume that Ω₁ and Ω₂ are simply connected and have a C² boundary, then and u₂ ∈ H²(Ω₂), see 15, p.198].

In the inverse problem, given a non-constant voltage Dirichlet input data f ∈ L²(∂Ω₁), we measure the corresponding Neumann current flux (7) in order to determine the solution pair (u, Ω₂).

When k =constant, the geometrical inverse problem given by Equations (2.2a–2.2e) is well-suited for the application of the BEM 11,12, or the MFS, as will be described in Section 3.

3. The method of fundamental solutions

The MFS may be viewed as a meshless BEM in which the governing potential field is approximated by a linear combination of the fundamental solutions of the operator of the governing equation under consideration. These fundamental solutions are given in terms of singularities which are positioned outside the domain of the problem. In contrast to the BEM, the MFS provides accurate approximations directly at points arbitrarily close to the boundary. Moreover, since no integration of shape functions over boundary elements is involved, it is considerably easier to implement than the BEM 16,17. The MFS has been successfully used in the past for the solution of free boundary problems and composite material problems, see 18 and 19, respectively.

In the MFS we seek approximations and to the solutions u₁ and u₂, respectively, of Equations (2.2a–2.2e) with k =constant, as linear combinations of fundamental solutions in the form 20 (8) (9) where G is a fundamental solution of the Laplace equation, given by (10) The singularities (sources) are located outside , i.e. in , while the singularities are located outside . In particular, and are placed on (moving) pseudo-boundaries and similar to ∂Ω₂, at a distance δ > 0 inwards and outwards, respectively. The remaining singularities are placed on a (fixed) pseudo-boundary similar to ∂Ω₁, as depicted in Figure 1. In the MFS, taking the pseudo-boundary similar to the boundary yields, in general, improved results as has been demonstrated in a recent study by Gorzelańczyk and Kołodziej 21. In (3.1) and (3.2), the singularities are fixed, whereas the singularities and move with ∂Ω₂ as will be described in the iterative process presented in the sequel.

For simplicity, we take d = 2, and without loss of generality, we shall assume that the (known) fixed exterior boundary ∂Ω₁ is a circle of radius 1; otherwise, we first conformally map the exterior of Ω₁ onto the exterior of the unit circle. As a result, the outer boundary collocation and source points are chosen as (11) (12) respectively, where and , and R > 1 is fixed.

We further assume that the unknown boundary ∂Ω₂ is a smooth, star-like curve with respect to the origin such that in polar coordinates its equation can be written as (13) where r is a smooth 2π-periodic function. (A similar but more tedious analysis can be performed in three dimensions through the use of spherical coordinates.)

Using (3.6), the flux continuity condition in (2.2d) can be rewritten as (14) which, since (15) becomes (16) The discretized form of (3.6) for ∂Ω₂ becomes (17) and we choose the boundary collocation and inner and outer source points as (18) and (19) The way the parameter η ∈ (0, 1) is chosen is discussed at the end of this section.

The coefficients in (3.1) and (3.2) and the radii in (3.10) can be determined by imposing the boundary conditions (2.2b), (2.2d) and (2.2e) in a least-squares sense. This leads to the minimization of the functional S : ℝ^2N × ℝ^N × (0, 1)^N → ℝ₊ defined by (20) where λ₁, λ₂ ≥ 0 are regularization parameters to be prescribed.

Remarks

i.	Equation (3.13) represents the discretized version of the continuous L2-norms.
ii.	The current flux data (2.2e) comes from practical measurements which are inherently contaminated with noisy errors and we, therefore, replace g by gϵ such that (21) In computation, the noisy data are generated as (22) where p represents the percentage of noise and ρj is a pseudo-random noisy variable drawn from a uniform distribution in [−1, 1] using the NAG 22 routine G05DAF.
iii.	In (3.13), the outward normal vectors are defined as follows: (23) (24) where i = (1, 0) and j = (0, 1). In (3.16b), we use the finite-difference approximation (25) with the convention that rN+1 = r1, r0 = rN, ϑN+1 = 0 and ϑ0 = 2π.
iv.	Since Equation (3.13) imposes 2M + 2N equations with 4N unknowns, in general, we shall take M ≥ N. Also, the constraints , are imposed during the iterative minimization by simple adjusting scaling, if necessary. Alternatively, one could have included these physical constraints into the functional (3.13), but the introduction of additional Lagrange multipliers, to be prescribed, would have further complicated the minimization problem.
v.	Since the inverse problem is ill-posed, in (3.13) the regularization terms λ1 {|c1|2 + |c2|2} and/or λ2|r|2 are added in order to achieve the stability of the numerical solution for u1, u2 and Ω2. The coefficients c1 and c2 are also penalized in the regularization since it is well-known that the MFS is rather ill-conditioned, especially when the input data contains noisy errors 23.

The minimization of (3.13) is carried out using the MINPACK 24, routine lmdif which minimizes the sum of the squares of nonlinear functions. In lmdif, the Jacobian is calculated internally by forward finite differences. It terminates when the convergence to a user-specified tolerance (tol) is achieved or when a user-specified maximum number of function evaluations (maxfev) is reached. Hence, the number of function evaluations performed (nfev) might, in some cases, be less than maxfev. In all calculations carried out in this study, the tolerance was set equal to tol = 10⁻¹⁰. An arbitrary initial guess for the unknowns such as c¹ = c² = 0, r = constant vector is taken to start the iterative procedure.

The MFS algorithm described in this section for solving the inverse problem (2.2) for isotropic piecewise homogeneous conductors can be extended to anisotropic conductors. In such a case, we replace the fundamental solutions (3.3) by (26) where K is the symmetric positive definite anisotropy tensor entering the Laplace–Beltrami equation (27) |K⁻¹| is the determinant of the inverse matrix K⁻¹ and .

4. Numerical examples

4.1. Example 1

We first consider an example for which an exact solution is known and given by, 25, (28) (29) (30) where r₀ ∈ (0, 1), k ≠ 1 and Ω₁ = B(0, 1).

This exact solution satisfies problem (2.2), with (31) and (32) In our numerical experiments we consider the case r₀ = 0.5. We also take k = 10. In the minimization of (3.13), the initial location of ∂Ω₂ was taken to be a circle of radius r⁽⁰⁾ = 0.3 and c¹ = c² = 0.

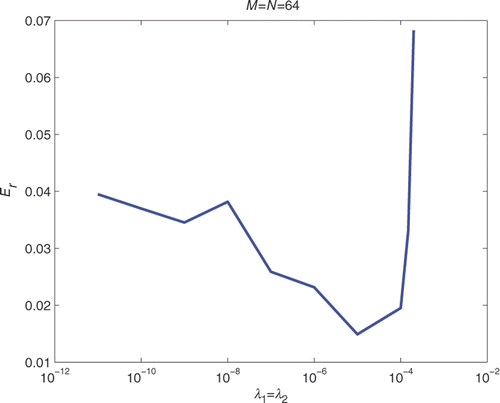
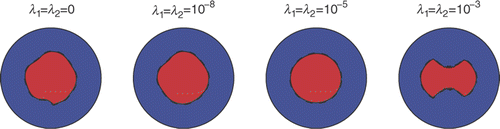
In Figure 2(a)–(d), we present the recovered contours obtained with no regularization for noise levels of p = 0, 1%, 3%, 5%, respectively, for nfev = 1000. The parameter η in (3.12) was chosen to be 0.6, and for each noise level we took N = M = 16, 32, 48 and 64. As expected, as the level of noise increases, the recovered contours start to deteriorate slightly. However, the numerical solutions presented in Figure 2 are still reasonably accurate and stable, even when no regularization is imposed in (3.13). In this case, the stability of the numerical solution is achieved by limiting the number of function evaluations to nfev=1000. Increasing the value of nfev to 5000, 10,000 and 15,000 tends to produce a slightly more unstable solution, as can be observed from Figure 3. In this case, the stability can be restored if one employs regularization, as shown in Figure 4. From this figure, it can be seen that for N = M = 64, p = 5% and nfev =15,000, the optimal value of the regularization parameters λ₁ = λ₂ in (3.13) appears to be of O(10⁻⁵).

Figure 2. Results with no regularization λ₁ = λ₂ = 0, nfev=1000, M = N ∈ {16, 32, 48, 64} and p ∈ {0, 1, 3, 5}%, for Example 1.

Figure 3. Results with no regularization λ₁ = λ₂ = 0, N = M = 64, p = 5% for various numbers of function evaluations nfev ∈ {1, 5, 10, 15} × 10³, for Example 1.

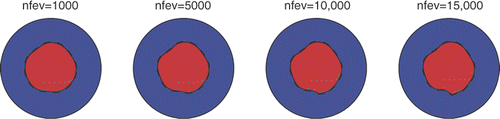
Figure 4. Results with N = M = 64, p = 5%, nfev=15,000 and various regularization parameters λ₁ = λ₂ ∈ {0, 10⁻⁸, 10⁻⁵, 10⁻³}, for Example 1.

In order to assess the accuracy of the numerical solution obtained in Figure 4, we calculated the maximum error in the final positions of the points defining the cavity, namely (33) Clearly, the smaller the E_r, the better the solution. In Figure 5 we present the plot of E_r versus the regularization parameters λ₁ = λ₂, from which it appears that the best results are indeed obtained for λ₁ = λ₂ = O(10⁻⁵).

Figure 5. E_r vs. λ₁ = λ₂, for N = M = 64, p = 5%, nfev=15,000, in Example 1.

Although not illustrated, it has been observed that smaller inclusions with radii up to r₀ = 0.1 = 10% of the characteristic size of the enclosing body Ω₁ were also detected with a reasonable accuracy. Obviously, smaller inclusions (tumours) are more difficult to detect both accurately and stably 5. On the other hand, in the extreme case when there is no inclusion, i.e. k = 1, the iterative algorithm terminates immediately by returning a vanishingly small unrealistic inclusion.

4.2. Example 2

In this example, we consider the more complicated bean-shaped inclusion ∂Ω₂ given by the radial parameterization (34) This example, which was also considered in 26, is significantly more difficult than Example 1 because of the presence of a sharp cusp-like portion mimicking a re-entrant corner.

The Dirichlet voltage data (2.2b) on ∂Ω₁ is taken as in 27 (35) We also take k = 6. Since in this case no analytical solution to problem (2.2) is available, the Neumann current flux data (2.2e) is simulated numerically by solving the well-posed direct problem (2.2a–2.2d) and (4.8), when ∂Ω₂ is given by (4.7), using the MFS with M = N = 96. In order to avoid committing an inverse crime, the inverse solver based on the minimization of (3.13) is applied using a different number M = N = 64. Furthermore, noise is added as in (3.15). The parameter η in (3.12) was chosen to be 0.2. The initial guess for ∂Ω₂ was taken to be a circle of radius r⁽⁰⁾ = 0.5 and c¹ = c² = 0.

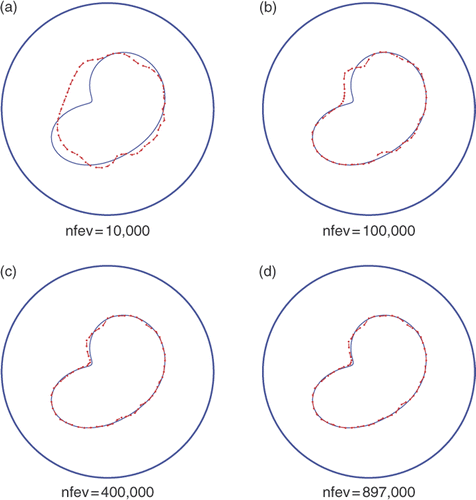
In Figure 6, we present the reconstructed and the exact shapes obtained with no noise and no regularization for various numbers of nfev. The results obtained for a sufficiently large nfev are in very good agreement with the exact shape. Note that maxfev was set to 1,000,000 but lmdif terminated for nfev=897,000 (Figure 6(d)), indicating that convergence was reached before the number of function evaluations reached maxfev.

Figure 6. Results with no noise p = 0, no regularization λ₁ = λ₂ = 0 and various numbers of function evaluations, for Example 2.

In Figures 7–9, we present the reconstructed and the exact shapes obtained with noises p ∈ {1, 3, 5}%, respectively, and no regularization for various numbers of nfev. The results indicate that visible instabilities start to manifest if no regularization is imposed and the amount of noise p and/or the number of function evaluations nfev increases. Note that maxfev was set equal to 1,000,000, but lmdif terminated for nfev=620,000 (Figure 7(d)), again indicating that the convergence was reached before the number of function evaluations reached maxfev.

Figure 7. Results with noise p = 1%, no regularization λ₁ = λ₂ = 0 and various numbers of function evaluations, for Example 2.

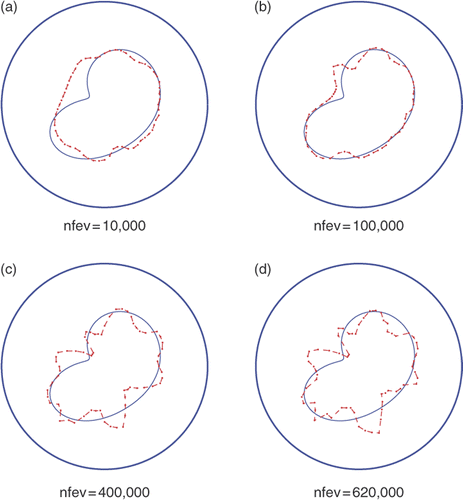
Figure 8. Results with noise p = 3%, no regularization λ₁ = λ₂ = 0 and various numbers of function evaluations, for Example 2.

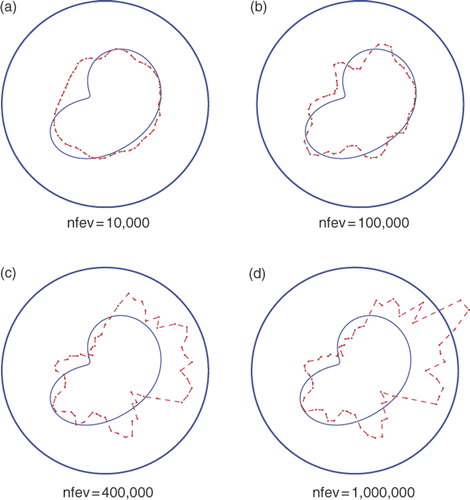
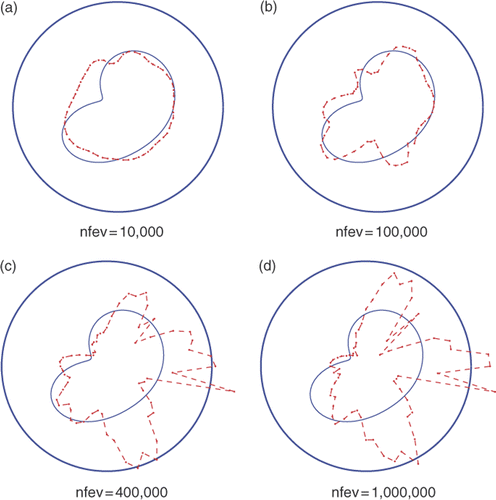
Figure 9. Results with noise p = 5%, no regularization λ₁ = λ₂ = 0 and various numbers of function evaluations, for Example 2.

In order to overcome the instability of the numerically reconstructed shapes, regularization is imposed in the functional (3.13). The numerical results with regularization for p ∈ {1, 3, 5}% are presented in Figures 10–12, respectively. Each of the figures presents numerical results for the reconstructed shapes when λ₂ = 0 and λ₁ ∈ {0, 10⁻⁶, 10⁻⁵, 5 × 10⁻⁵, 10⁻⁴, 10⁻³} and the maximum number of function evaluations is prescribed as maxfev=1,000,000. It is noteworthy that, unlike the results of Figures 7–9, in Figures 10–12 the presence of the regularization λ₁ > 0 can reduce the number of function evaluations nfev, i.e. convergence is reached for fewer function evaluations than the prescribed number maxfev=1,000,000.

Figure 10. Results with noise p = 1%, prescribed maxfev = 10⁶ and various regularization parameters λ₁ ∈ {0, 10⁻⁶, 10⁻⁵, 5 × 10⁻⁵, 10⁻⁴, 10⁻³}, λ₂ = 0, for Example 2.

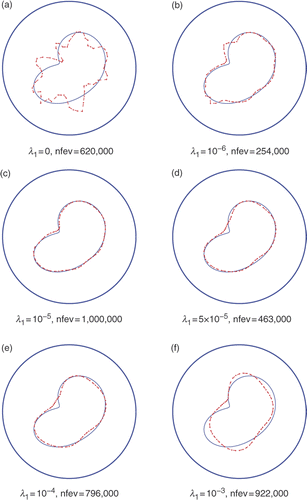
Figure 11. Results with noise p = 3%, prescribed maxfev = 10⁶ and various regularization parameters λ₁ ∈ {0, 10⁻⁶, 10⁻⁵, 5 × 10⁻⁵, 10⁻⁴, 10⁻³}, λ₂ = 0, for Example 2.

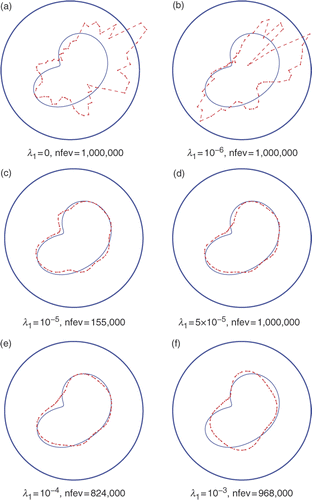
Figure 12. Results with noise p = 5%, prescribed maxfev = 10⁶ and various regularization parameters λ₁ ∈ {0, 10⁻⁶, 10⁻⁵, 5 × 10⁻⁵, 10⁻⁴, 10⁻³}, λ₂ = 0, for Example 2.

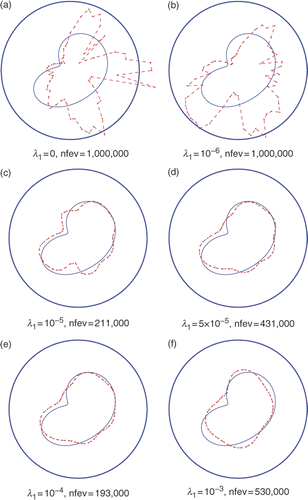
From Figures 10–12 it can be observed that the best results are obtained for λ₁ between 10⁻⁵ and 10⁻⁴.

5. Conclusions

A novel numerical method based on a regularized iterative MFS has been developed for the approximate solution of the inverse conductivity problem. The MFS was employed because, while it shares most of the advantages of the BEM for such geometrical inverse problems, it is considerably easier to implement and does not involve potentially troublesome integrations. In the inverse analysis a fast direct solver is often needed with iterative minimization procedures and, especially in higher dimensions, the MFS, being meshless, is much faster than other domain and boundary discretization methods. There is, however, a compensating cost to be paid for the ease of implementation of the MFS, for example, the method is rather ill-conditioned, especially when the input data contains noisy errors 23. The MFS was applied to two such problems with known and unknown analytical solutions, and the effects of the number of function evaluations and regularization was studied for noisy data up to 5%. The numerical results indicate that accurate reconstructions with reasonable stability against noisy data can be produced with the proposed method. Further numerical experiments indicated that for a noisy level above 10% the reconstructions began to deteriorate. While in this numerical study the regularization parameters λ₁ and λ₂ were chosen by trial and error, more rigorous criteria such as the discrepancy principle will be investigated in a future study. It is also possible that stopping the iterative minimization process at an appropriate threshold (depending on the amount of noise) plays the role of regularization. Future work will also involve extending the numerical implementation of the MFS to the retrieval of multiple inclusions and to three-dimensional problems.

Acknowledgements

The authors would like to thank the University of Cyprus for supporting this research. The comments of the referees and the associate editor are also gratefully acknowledged.