Abstract
In this study, mass transfer in deformed porous materials is investigated theoretically and analytical solutions of mass transfer equations for investigated materials are derived. In order to determine the variation of porosity degree of the material versus time and to estimate the region where the variation of effective diffusion coefficient is regular, an inverse ill-posed problem is solved by considering the experimental data concerned with the drying of the porous material. The numerical calculations of concentration profiles and experimental results concerned with the drying of the materials in a magnetic field are given.
Nomenclature
| ε | = | porosity of material |
| ε0 | = | initial porosity of the material |
| B | = | intensity of the magnetic field, T |
| X | = | moistness degree, kg m3−1 |
| X0 | = | initial moistness degree, kg m3−1 |
| R | = | radius of pore, m |
| μ | = | molecular mass, kg |
| ηP | = | sinuosity of pore |
| T | = | temperature, °C |
| M | = | moisture concentration in the material, kg m3−1 |
| Mp | = | moisture concentration in equilibrium with flux, kg m3−1 |
| DM | = | magnetic diffusion coefficient |
| DT | = | molecular diffusion coefficient, m2 s−1 |
| D* | = | effective diffusion coefficient, m2 s−1 |
| αM | = | magnetic polarization coefficient |
| ξS | = | shear viscosity of the porous medium, N · s m−2 |
| σD | = | internal deforming strain, N m−2 |
| l | = | distance calculated along the current line, m |
| s0 | = | cross-section area of the pore channel, m2 |
| v | = | air flow speed, m s−1 |
| ω | = | frequency of magnetic field, Hz |
| MR | = | relative moisture concentration |
| = | experimental values of relative moisture |
1. Introduction
Currently, the drying of porous materials is widely used in food and chemical industries and agriculture. There are many studies concerned with the experimental investigation of the drying of porous materials Citation1–4. In these studies, several empirical expressions which allow us to evaluate the dispersion of moisture concentration and diffusion coefficient versus time are derived by considering experimental data.
In references Citation5–7, the mass transfer problems in convective drying processes are analysed theoretically. The analytical solutions of convective diffusion equations are given to determine the criteria dependence of Sherwood number on Reynolds and Schmidt numbers for molecular transport phenomena of the moisture on the porous layer.
Drying processes in porous material are characterized by complex physical phenomena, such as movement of the moisture in irregular capillaries, phase transitions, etc. In reference Citation8, the density of the material and the variation of the porosity are investigated experimentally by considering the relative moistness degree and the correlation expression given below is obtained for the temperature interval of 30–60°C.
(1)
In Ref. Citation9, the experimental results denoting the dependence of diffusion coefficient on drying time are given for the temperature interval of 85–105°C since the moistness ratio depends on the drying time. It is necessary to emphasize that the porous layers of the material are deformed by the effect of the strains conducing the internal deformation and are intensified. Hence, the material drying processes accompany the change in the shape, volume and geometry of the material. In many theoretical and experimental studies concerned with the drying of porous materials, it is seen that mass transfer in these kinds of materials depends on the deformation characters including sliding, pressing and bending Citation8,Citation9. The reason for that is the dependence of the effective diffusivity coefficient of the material on the porosity degree and internal deforming strains.
Even the porous medium, including the solid phase are compressible. The evaporation of the liquid in the pores by drying causes the changes in the porosity degree, density and effective diffusivity coefficient of the material by time. However, it must be emphasized that the internal strains occurring at relatively high temperatures cause the formation of cracks and degradation in the structure of the material Citation10,Citation11. The basic mechanism of the drying process in the volume of porous material can be explained as follows:
| a. | The transport of the moisture from material volume towards the surface by diffusion. | ||||
| b. | The transport of air flux from the material surface towards the volume by convective diffusivity. | ||||
The mass transfer process in porous materials is determined with the geometry of the pore (e.g. sinuosity, pore dimensions, etc.). This situation is considered in the expression of effective Knudsen diffusivity coefficient as
(2)
where r is the radius of pore, T the temperature, μ the molecular mass, ε the porosity of material and
the sinuosity of pore. The most important stage in the drying process is the convective transport of the vapour from the material surface into the volume by considering the flow character (laminar, turbulent). The transport of vapour from the material surface into the volume for greater values of the Reynolds number is achieved by turbulent diffusion which depends on turbulence characteristics (e.g. specific energy dissipations, turbulent scales, etc.) Citation12,Citation13. The drying processes of porous materials can be intensified by using different methods, such as electrical and magnetic fields. In this case, the moisture flux transported over the porous material consists of the fluxes resulting from the diffusivity and the effect of the magnetic field.
(3)
where DM depends on the frequency of the magnetic field.
In the light of the explanations mentioned above, the determination of the diffusion coefficient in the volume of both material and gas flux is converted to the problem of the evaluation of the variable values of effective diffusivity depending on the time and porosity degree. In this study, the mass transfer during the drying of the porous medium is investigated by considering the magnetic field.
2. Mass transfer in drying processes by considering the shrinkage of the structure
Drying processes accompanied by heat-mass conversion enables physical and micro-structural changes in the porous material. The most important internal parameters in the drying of porous material are density and porosity parameters that are defined by the expression
(4)
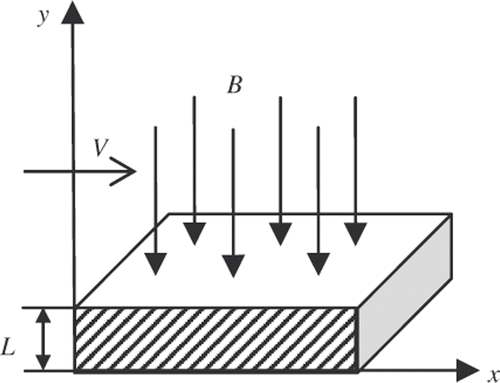
where ρ and ρp are the densities of the medium and porous material, respectively. There is a relationship between effective diffusivity coefficient and these parameters. The experimental results about the influence of moisture and temperature on the drying process demonstrate that the density and diffusion coefficient of the material decrease monotonously after they reach a maximum in the first stage of drying Citation14–16. So, the drying of deformed porous materials is characterized by the variable values of the density, porosity degree and effective diffusion coefficient of the material. The mass transferred from the planar lamina shaped isotropic porous material () located in the magnetic field is expressed for the cases of fixed temperature and laminar flow as
(5)
where Vx and Vy are the components of velocity of air flow in x and y directions.
The variation of the lamina porosity as a result of the shrinkage of the laminas by the effect of internal deforming strains is given as Citation17
(6)
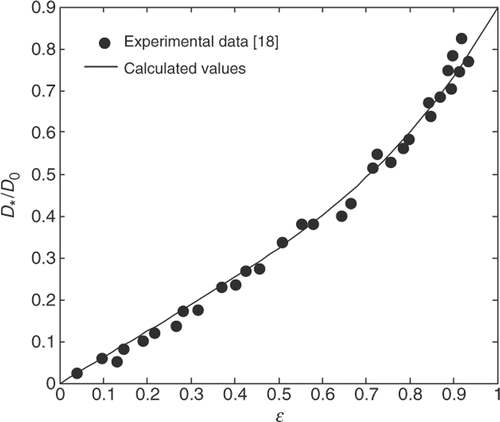
By utilizing many experimental investigations intended to determine the effective diffusivity coefficient in the porous medium, the following empirical expression is obtained Citation18
(7)
The variation of this expression versus porosity is illustrated in . For the values of ≪ 0.55, by considering the sinuosity of the pores, this expression is converted to a linear dependence given below
(8)
Figure 2. Dependence of relative effective diffusivity coefficient on the porosity. The experimental data were taken from Satterfield Citation18.
In general, the effective diffusivity coefficient is a function of coordinate and time in inhomogeneous and anisotropic porous laminas.
Let us analyse the solution of Equation (5) in the absence of a magnetic field and at the low values of the Reynolds number . If Equation (5) is rearranged by considering this approximation which is available in the cases: (1) the moisture in the pores is evaporated; (2) the diffusion coefficient is variable and (3) the deformations are small (
), then the following equations are obtained:
(9)
(10)
In the case that the effective diffusivity coefficient varies only as a function of time, the following expression can be written by considering Equation (8)
(11)
where
If Equation (9a) is rearranged by defining new variables, such as ,
and making some transforms for the one-dimensional transfer, then we obtain
(12)
The independent variable of in Equation (12) is quantitatively equal to the stationary transfer potential at the condition of
and expresses the spatial coordinates. In order to solve Equation (11), it is suitable to approximate the
function as
(13)
where α and b are any constants. In this case, by inserting Equation (12) into Equation (11) and making Laplace transform Citation19, we obtain
(14)
(15)
where λ is complex variable,
the image function and
the original function corresponding to the image function. The solution of Equation (13) is found by substituting
in modified Bessel equations obtained by inserting Equation (12) into Equation (13) as
(16)
where
and
are the first- and second-type modified Bessel functions, respectively. Let us find the special solutions of Equation (15) satisfying the boundary conditions given below:
(17)
(18)
The first term at the right-hand side of Equation (15) satisfies the boundary condition given by Equation (16b), then we obtain
(19)
By considering asymptotic equality of and the condition given by Equation (16a), the following expression is obtained for the low values of z:
Hence, if Equation (17) is rearranged then we get
(20)
(21)
The original of the image function is an incomplete Gamma function and obtained as
So, if the inverse Laplace transform is applied to Equations (18a and 18b) by considering then we get
(22)
(23)
If we substitute in Equation (19b) and utilize
expression, then we obtain
When Equation (19a) is differentiated with respect to t by considering Equation (19b), we obtain
(24)
It can be easily demonstrated that the solution given in Equation (20) satisfies Equation (12) and boundary values given in Equation (16). In this case, by considering boundary conditions, the solution defined by Equation (15) is rearranged analogously with Equation (20), and the following expression is obtained:
(25)
where
.
Equation (21) expresses the moisture transport for porous materials in the general case. As seen, since the solution of Equation (21) for arbitrary function is difficult, the equation can be solved numerically or by using exponential series. But, if the moisture concentration in the porous medium reaches the equilibrium state of
in l = L condition, then the solution defined by Equation (21) can be expressed as
(26)
If α = 1, then the right-hand side of Equation (22) converts to the probability integral. Hence, we obtain
(27)
where
(28)
(29)
and the effective diffusion coefficient D* is determined by using Equation (10).
It is obvious that the solution defined by Equation (21) is nonlinear in the case of , and so the dispersion of moisture concentration will be different from the solution defined with Equation (23). By using Equation (23), the vapour flux leaving the lamina surface S is obtained as
(30)
In this case, the unitless vapour flux or Sherwood number and its mean value will be found as
(31)
(32)
In the above expressions, while explaining the calculation of the Sherwood number, the convective transport of vapour from the surface into the gas flux is not considered. In the case that convective transport is considered, the several parameters of gas flow and vapour (e.g. temperature, moisture, turbulent, molecular diffusion coefficient, viscosity, etc.) must be taken into account.
3. The solution of an inverse ill-posed problem
The determination of the diffusion coefficient or the variable η described in expression (24b) by considering the measured and calculated values of relative moisture concentration is an inverse ill-posed problem Citation20–22. The estimation of effective diffusion coefficient is expressed by using the inverse problem Equation (23) as
(33)
The errors occurring in the experimental measurements and the calculation of moisture concentration result in big mistakes in the estimation of η parameter and the effective diffusion coefficient. So, the problem defined by Equation (27) is ill-posed. The basic criteria for the evaluation of the effective diffusion coefficient in the solution of inverse problem is the quadratic relative error magnitude, and it is expressed as
(34)
where
is the experimental values of moisture concentration.
However, it is required to determine the interval where the inverse problem is regular. In other words, the sensitivity of η parameter against the errors in experimental measurements and the deviations in the calculation of moisture concentration must be determined. If Equation (27) is differentiated with respect to moisture concentration, then we obtain
(35)
By inserting the derivative of Equation (23) with respect to η parameter into Equation (29) and making some simple transforms, the following expression is obtained for small variations:
(36)
In this expression
and
is the absolute error. So, Equation (23) determines the interval where Equation (27) is regular for sufficiently small values of
relative error. By using Equations (30) and (24b), the following expression is obtained for the effective diffusion coefficient
(37)
where the values of
change between 0 and 1, namely
As seen from Equation (31), the error occurring while finding the effective diffusion coefficient is determined by the square of the error occurring in the measurement of moisture concentration. So, the relative error is in the case of
,
and
. In this case, the infinite small increases of
correspond with the infinite small variations of
, namely the inverse problem concerned with the evaluation of effective diffusion coefficient is conditionally well-posed or ill-posed according to the approximation given in Ref. Citation20.
4. Experimental investigation of magnetic drying processes
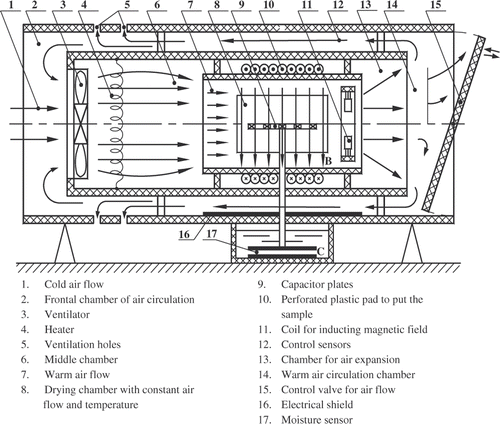
The investigation of the drying processes of porous materials in a magnetic field demonstrates that the parameters of the magnetic field affect the rate of moisture transport in the material. In the literature, the studies concerned with the drying of materials in magnetic and electrical fields are insufficient Citation23–26.
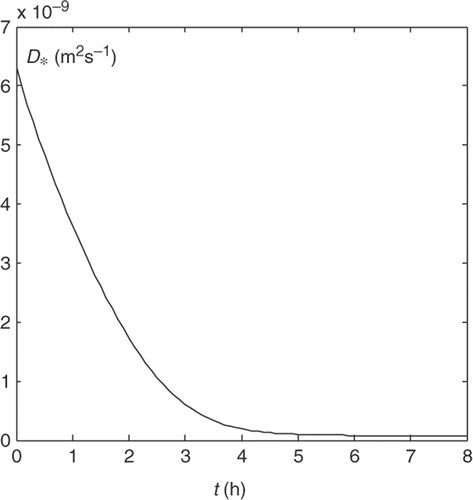
In these studies, the drying processes have been investigated experimentally and some empirical expressions have been derived for drying kinetics. In our study, the experimental setup seen in has been prepared to perform the drying process in different conditions. The experiments have been performed under the conditions of temperature T = 40–60°C, air flow speed v = 1.0–2.0 m s−1 and the frequency of magnetic field . In order to dry a laminar potato having an initial thickness of L = 10 mm, it is located in a medium where temperature is 50°C and air flow speed is 1.75 m s−1 (), and it is exposed to a magnetic field effect in different frequencies. The variation kinetics of the effective diffusivity coefficient is seen in in accordance with the experimental data and the criteria defined by Equation (28). In , the experimental results expressing the time dependence of normalized moisture concentration are illustrated at
and
. In these figures, the effects of the density, frequency and diffusion coefficient of the magnetic field on the drying processes of porous materials are illustrated.
Figure 5. Dependence of normalized concentration on drying time for different magnetic field frequencies under the conditions of T = 50°C and v = 1.75 m s−1.
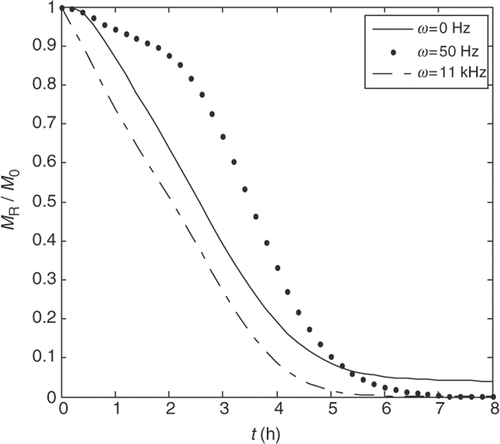
The analytical solution of the effect of a magnetic field on the drying processes of porous materials having a variable diffusivity coefficient seems to be impossible. So, the parameters of the magnetic field, such as the empirical terms including the frequency of the magnetic field, is required to be involved in the solution defined by Equation (23) in the absence of magnetic field. If Equation (23) is rearranged according to this approximation, then we obtain
(38)
where m is a coefficient calculated by using experimental data and defined as
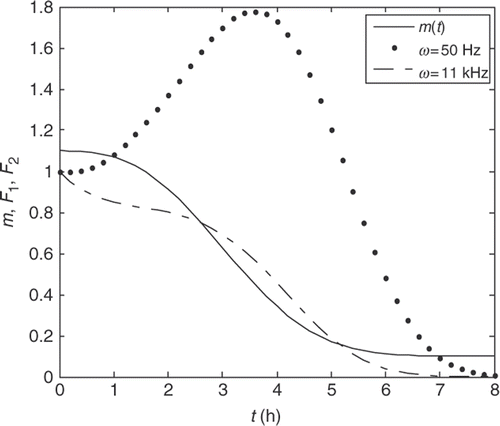
. In , the normalized moisture concentration values which are obtained from experiments and calculated numerically by using Equation (32) are illustrated for potato.
function is empirically determined by using experimental data as
. By considering the frequency of the magnetic field, the experimental values of a1, a2 and a3 coefficients are given in .
Table 1. The dependence of coefficients on the frequency of magnetic field.
As seen from the table, while the parameters of the magnetic field affect the coefficient strongly, they affect a2 and a3 coefficients weakly.
In , the dependences of and
on time are illustrated for different frequency values. By using
formula, the mean value of the effective diffusivity coefficient has been obtained as
. By considering that L0 and L∞ are initial and stabilized thicknesses of the material, the variation of the mean thickness of dried material resulting from the deformation can be determined as
. As we know, the parameters of the magnetic field affect the magnitude of the effective diffusivity coefficient, considerably. This means that there is a definite correlation between molecular diffusion and magnetic diffusion. In other words, it can be thought as if the effective diffusivity coefficient is the addition of magnetic and molecular diffusivities. It is not possible to understand the analytical theory of drying process in the magnetic field in the absence of definite values about magnetic diffusion. So, the usage of empirical expressions to explain the experimental results about the drying process in the magnetic field confirms itself at an acceptable rate.
5. Conclusion
In this study, by considering the magnetic field, the calculation of the drying processes in a deformed porous medium is proposed. It is emphasized that the effective diffusivity coefficient and the porosity of lamina are functions of time in the drying processes accompanying the deformation and collapse of the material.
The analytical solution of the mass transfer equation given by Equation (25) is presented in the absence of a magnetic field. By considering the effect of the magnetic field, the variation kinetics of the effective diffusivity coefficient and normalized moisture concentration are given. We must mention that by using the minimum condition of quadratic criteria defined by Equation (28), the inverse problem concerned with the evaluation of effective diffusivity coefficient can be accepted as a conditional well-posed problem. There are big deviations between the values of the effective diffusivity coefficient determined according to the criteria given in Equation (23) and the values of the effective diffusivity coefficient determined for different temperature, air flow and magnetic field frequency. The reason for this can be explained by the linearity of f function in the case of α = 1, or deformation of the structure in long time drying. To eliminate these deviations, a semi-empirical expression, given by Equation (29), considering the effect of the magnetic field and other factors on the drying processes is derived by utilizing Equation (22).
The application of the magnetic field recovers the drying process of porous materials considerably, and shortens the drying time. This also reduces the energy expenses in drying processes. Internal and external configurations occurring in the materials in the drying processes of porous materials affect the porosity degree and effective diffusivity coefficient of the material, considerably. This is primarily explained by the anisotropy in the geometry of the material and in this case the mass transfer cannot be expressed by simple transfer equations.
References
- Maskan, M, 2001. Drying shrinkage and rehydration characteristics of kiwi fruits during not air microwave drying, J. Food Eng. 48 (2001), pp. 177–186.
- Tayaraman, K, and Gupta, DK, 2005. Handbook of Industrial Drying. New York: Marcel Dekker; 2005.
- Karim, MA, and Hawlader, MN, 2005. Drying characteristics of banana: Theoretical modeling and experimental validation, J. Food Eng. 70 (2005), pp. 35–43.
- Hayaloglu, AA, Karabulut, I, Alpaslan, M, and Kelbaliyev, GI, 2007. Mathematical modeling of drying characteristics of strained yoghurt in a convective type tray-dryer, J. Food Eng. 78 (2007), pp. 109–117.
- Landau, LD, and Lifshitz, EM, 1953. Mekhanika Sploshnykh Sred (Mechanics of Continuous Media). Moscow: Nauka; 1953.
- Bird, RR, Stewart, WE, and Lightfoot, EN, 1960. Transport Phenomena. London: John Wiley; 1960.
- Lykov, AV, 1972. Teplomassoobmen Spravochnik (Heat and Mass Transfer: A Reference Book). Moscow: Energiya; 1972.
- Al-Muhtaseb, AH, McMinn, WA, and Magee, TR, 1960. "Shrinkage, Density and Porosity Variations during the Convective Drying of Potato Starch Gel". In: Proceedings of the 14th International Drying Symposium. Sao Paulo, Brazil. 1960.
- Ježek, D, Tripalo, B, Brnčić, M, Karlović, D, Vikić-Topić, D, and Herceg, Z, 2006. Modeling of convective carrot drying, Croat. Chem. Acta 79 (2006), pp. 385–395.
- Wang, N, and Brennan, JG, 1995. Changes in structure density and porosity of potato during dehydration, J. Food Eng. 24 (1995), pp. 61–76.
- McMinn, WA, and Magee, TR, 1997. Physical characteristics of dehydrated potatoes, J. Food Eng. 33 (1997), pp. 37–48.
- Altunbaş, A, Kelbaliyev, G, and Ceylan, K, 2002. Eddy diffusivity of particles in turbulent flow in rough channels, J. Aerosol Sci. 33 (2002), pp. 1075–1086.
- Levich, VG, 1959. Fiziko-Khimicheskaya Gidrodinamika (Physico-chemical Hydrodynamics). Moscow: Fizmatgiz; 1959.
- Hatamipour, MS, and Mowla, D, 2003. Correlation for shrinkage, density and diffusivity for drying of maize and green peas in a fluidized bed with energy carrier, J. Food Eng. 59 (2003), pp. 221–227.
- Pinto, LA, and Tobinaga, S, 2006. Diffusive model with shrinkage in the thin-layer drying of fish muscle, Drying Technol. 24 (2006), pp. 509–516.
- Rotstein, E, 1987. "The prediction of diffusivities and diffusion related properties in the drying of cellular foods". In: Jowitt, R, Escher, F, Kent, M, McKenna, BM, and Roques, M, eds. Physical Properties of Foods. London: Applied Science Publishers; 1987. pp. 131–145.
- Kelbaliyev, GI, 1985. Mathematical description of nonstationary processes in isotropic porous media by quasicontinious models, Theor. Found. Chem. Eng. 19 (1985), pp. 143–149, (in Russian).
- Satterfield, CN, 1970. Mass Transfer in Heterogeneous Catalysis. Cambridge, MA: MIT Press; 1970.
- Dech, G, 1965. Guide to Practical Application of Laplace Transform. Moscow: Nauka; 1965, (in Russian).
- Tikhonov, AN, and Arsenin, V, 1974. Methods for Solving Ill-posed Problems. Moscow: Nauka; 1974, (in Russian).
- Kanevce, LP, Kanevce, GH, and Dulikravich, GS, 2005. Application of inverse concepts to drying, Therm. Sci. 9 (2005), pp. 31–44.
- Kanevce, GH, Kanevce, LP, Dulikravich, GS, and Orlande, HRB, 2005. Estimation of thermophysical properties of moist materials under different drying conditions, Inverse Probl. Sci. Eng. 9 (2005), pp. 341–353.
- Sadek, SE, Fax, RG, and Hurwitz, M, 1972. The influence of electrical fields on convective heat and mass transfer from a horizontal surface under forced convection, J. Heat Transfer, Trans ASME 94 (Series C, 2) (1972), pp. 144–148.
- Knorr, D, and Angersbach, A, 1998. Impact of high electric field pulses on plant membrane permeabilization, Trends Food Sci. Technol. 9 (1998), pp. 185–191.
- Ade-Omowaye, BIO, Rastogi, NK, Angersbach, A, and Knorr, D, 2001. Effects of high hydrostatic pressure or high intensity electrical field pulse pre-treatment on dehydration characteristics of red paprika, Innovative Food Sci. Emerging Technol. 2 (2001), pp. 1–7.
- Aladjadjiyan, A, and Ylieva, T, 2003. Influence of stationary magnetic field on the early of the development of tobacco seeds, J. Cent. Eur. Agr. 4 (2003), pp. 131–137.