Numerical differentiation for periodic functions

Abstract

In this article we consider the numerical differentiation of periodic functions specified by noisy data. A new method, which is based on the truncated singular value decomposition (TSVD) regularization technique of a suitable compact operator, is presented and analysed. It turns out the new method coincides with some type of truncated Fourier series approach. Numerical examples are also given to show the efficiency of the method.

Keywords:

• numerical differentiation
• ill-posed problem
• TSVD method
• regularization method
• truncated Fourier series

AMS Subject Classifications::

• 65J20
• 65J22

1. Introduction

Numerical differentiation is the problem of determining derivatives of a function from its values on an interval or some scattered points. It arises from many scientific researches and applications, e.g. the identification of the discontinuous points in an image process 1; the problem of solving the Abel integral equation 2; the problem of determining the peaks in chemical spectroscopy 3, some inverse problems in mathematical physics equations 4, etc. The main difficulty is that it is an ill-posed problem, which means small errors in the measurements of a function may lead to large errors in its computed derivatives 4,5. A number of techniques have been developed for numerical differentiation 4–11. In 10, a theoretical result has been obtained for arbitrary numerical differentiation of a function in Hⁿ[0, 1]. But in their method, different solution processes are used for different n. In this article, we will give a method for numerical differentiation of periodic functions. In our method, the solution processes will be uniform for different n, which means that the method is self-adaptive.

One type of method of the numerical differentiation problem is to transform it into an operator equation of the first kind. In fact, for given g ∈ H¹[0, 1], finding f = Dg = g′ is equivalent to solving the Volterra integral equation of the first kind (1) In 11, a modified operator of K₁ in (1) has been presented for general functions. In this article, another modified operator will be considered for periodic functions. For the new operator, better properties will be obtained and we can successfully deal with high-order differentiation, as well as first order. In the present situation a singular system of the new operator can be obtained easily. Therefore, it seems natural to use the truncated singular value decomposition (TSVD) method for our problem.

The article is organized as follows. In Section 2, we will discuss a singular system and the properties of the new operator. In Section 3, an algorithm based on the TSVD method for first-order numerical differentiation is proposed and analysed, and in Section 4 it is extended to high-order differentiation. Some numerical results are given in Section 5, which show that the new method works well.

2. Singular system and its properties

Some notations will be used in the sequel. Let ℂ₁ = ℂ₁(ℝ) denote the space of continuous functions with period 1, the associated norm is given by (2) and let denote the space of square integrable functions on the interval [0, 1] with period 1, the associated norm is given by (3) Finally, let

It is obvious that the operator K₁ is the inverse of the following operator T₁: (4) We consider now a slightly different operator T defined by (5) where

In this article, ⟨·, ·⟩ denotes the inner product in space L². Then T is invertible and K = T⁻¹ : is given by (6) K is compact and its adjoint operator K* = −K. It can be verified that the eigenproblem K*Ke = λe is equivalent to (7) Thus the eigenvalues of K*K are There are exactly two eigenfunctions corresponding to each eigenvalue λ_l: Therefore the singular values and the corresponding singular functions of operator K can be taken as (8) For a function , the solution to the equation (9) can be expressed by the singular system of the operator K as follows 5: (10) The above formula shows that the expansion of function f by the singular functions is just the Fourier series of f on [0, 1]. The important thing is that these Fourier coefficients can be calculated in terms of the singular values and the Fourier coefficients of the given function g.

In the following, we discuss the generalized smooth scale of a function with respect to the operator K, which is a key index concerning convergence rates of a regularization method 5. We need some results of Fourier series. For a periodic function φ(t) with period 2l, its Fourier series has the form or where

LEMMA 2.1 12

Suppose that function φ(t) is 2l-periodic and of bounded variation on [0, 2l], and let be the Fourier coefficients of φ(t). Then (11)

Suppose now , then from integration by parts we have (12) and (13) On the other hand, we know that for a function , , if and only if 4 (14) Thus from Lemma 2.1, we have the following theorem.

THEOREM 2.2

Suppose , then we have (15) Moreover, if Dⁿ f is of bounded variation, then (16) Especially if , then (17)

Proof

If , let . If n is even, then we have (18) If n is odd, then we let . Then h₁ = −K*h, and therefore (19) It is well known that (20) Hence (14) holds. Moreover, if Dⁿ f is of bounded variation, then (15) results from Lemma 2.1 and (12–13).▪

Remark 1

Generally, a function is not in . Let (21) Then and . Thus the differentiation problem for g can be transferred to solving the following operator equation (22)

Remark 2

For a non-periodic function g ∈ Hⁿ[0, 1](e.g. g(t) = exp(t)), let be the periodic continuation of function g from the interval [0, 1] to all ℝ with period 1. Generally, we have , even if we let (23) we only have . Therefore, the present method can only be used in the following when the periodic continuation does not break the smoothness of the function.

3. First-order differentiation

Instead of g(s), in practice we usually only have perturbed data g^δ(s). Furthermore, the condition (24) is assumed with δ being a known error level. The perturbed form of Equation (21) is (25) where (26) We have (27) and it is clear that . The TSVD solution to Equation (24) can be given as follows: (28) where m = m(δ) is determined by the discrepancy principle (29) From the theory of TSVD method we have the following theorem.

THEOREM 3.1 13

Let g^δ satisfy (23), τ > 1, is defined by (27) and (28). Suppose , ν > 0, then (30)

and (31) where (32) From Theorem 3.1 and Remark 1, we have the following result.

COROLLARY 3.2

Suppose ‖g^δ − g‖ ≤ δ, f = g′, , then we have (33) Moreover, if Dⁿ g is of bounded variation, then for , the TSVD solution defined above satisfies (34)

4. High-order differentiation

Let (35) and the operator is compact. For a function , its k-th derivative h = D^kg(1 ≤ k ≤ n) satisfies the equation (36) The perturbed version of Equation (35) is (37) Similar to the discussion in the above, the singular values and the corresponding singular functions of operator B_k can be taken as (38) If k is even, (39) If k is odd, (40) Analogously, we have the following theorem.

THEOREM 4.1

Suppose , then (41) Moreover, if Dⁿ h is of bounded variation on [0, 1], then (42) Especially, if , then (43)

The TSVD solution to Equation (36) is given by (44) where m = m(δ) is determined by the discrepancy principle (45)

Remark 3

We have (46) Therefore, for 1 < k ≤ n, the value of m in (43) is equal to the one in (28).

We have the following result.

THEOREM 4.2

Let g^δ satisfies (23), τ > 1, is defined by (42) and (43), Suppose , ν > 0, then (47) and (48)

Especially, we have the following corollary.

COROLLARY 4.3

Suppose , h = D^kg, g^δ satisfies (23), τ > 1, is defined by (42) and (43), then we have (49) Moreover, if h is of bounded variation on [0, 1], then the TSVD solution h^δ defined above satisfies (50)

Next, we will give a uniform convergence result.

LEMMA 4.4 14

If h ∈ H¹[0, 1], then (51) where C₀ is a constant independent of f.

It can be verified that if is the TSVD solution to the equation , then is the TSVD solution to the equation . Thus from Corollary 4.3 and Lemma 4.4, we have the following theorem.

THEOREM 4.5

Suppose and Dⁿg is of bounded variation on [0, 1], and the estimate (23) is fulfilled, then converges uniformly to D^kg as δ → 0, and , (52)

5. Numerical examples

In this section, we present numerical results of some test examples. In all cases, the discretization knots t_i = ih, i = 1, …, N, with N = 2048, h = 1/N. The perturbed discrete data is given by where are generated by function (2 × rand(N + 1, 1) − 1) × δ₁ in Matlab.

In computation, one has to calculate the integrals First we obtain the cubic spline interpolation function s(t) for non-oscillatory function g^δ(t) with the periodic boundary conditions In this case, the function s(t) can be regarded as the perturbed data of function g(t) and the integrals where M_i = s″(t_i). We only need the error estimates δ in As in our example the error satisfies a uniform distribution, we let in practical computing.

All examples are computed by using Matlab with the parameter τ = 1.01. The L²-norm relative errors and the maximum-norm relative errors are given in Tables 1 and 2 to verify the theoretical results. Figures 1 and 2 with δ₁ = 0.5 and 0.1 compare qualitatively the computed solutions and the exact ones.

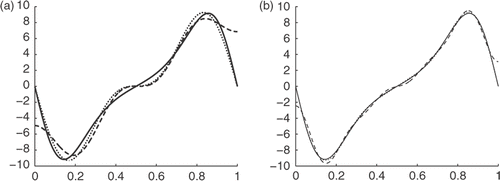
Let us first consider the numerical comparison between the present method (M1) and the method in 11 (M2) for computing the first-order derivative.

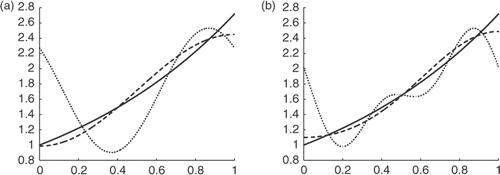
Here and in what follows, the solid curve means the exact solution, while the dotted–dashed curve indicate the solutions of M1 and M2, respectively.

Example 1

First we consider the periodic function From Corollary 3.2 and Theorem 3.1 in 11, we have that the convergence rates of M1 and M2 are O(δ) and O(δ^3/5), respectively. The numerical results are shown in Table 1 and Figure 1.

The numbers in columns 3, 4 and 7, 8 show that the results of M1 are much better than M2 for periodic function. Moreover, the numbers in columns 5 and 9 exhibit that the ratios are stable when δ → 0.

Figure 1. Comparison of M1 and M2 for periodic function: (a) δ₁ = 0.5 and (b) δ₁ = 0.1.

Table 1. Comparison of M1 and M2 for periodic function.

	M1				M2
δ1	m				m
1e−1	6	0.0180	0.0199	1.7511	10	0.0864	0.3378	2.6800
1e−2	8	0.0022	0.0025	2.1640	24	0.0203	0.1192	2.5061
1e−3	10	0.0003	0.0004	2.5210	54	0.0058	0.0482	2.8670
1e−4	12	2.42e−5	3.43e−5	2.3529	124	0.0017	0.0198	3.3202

Example 2

We consider the non-periodic function From Remark 2, Corollary 3.2 and Theorem 3.1 in 11, we have that the convergence rates of M1 and M2 are O(δ^1/3) and O(δ^3/5), respectively. The numerical results are shown in Table 2 and Figure 2. The numbers in columns 3, 4 and 7, 8 show that the results of M1 are inferior to the ones of M2.

These two examples show that the present method is fit for solving the derivatives of periodic smooth functions.

Next, we give the numerical results of the high-order derivatives of Example 1 in Table 3 and Figure 3. All results show that the new method works well.

Figure 2. Comparison of M1 and M2 for non-periodic function: (a) δ₁ = 0.5 and (b) δ₁ = 0.1.

Figure 3. Results of high-order derivatives of Example 1: (a) second-order derivative with δ₁ = 0.1 and (b) third-order derivative with δ₁ = 0.1.

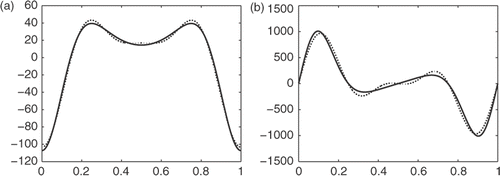
Table 2. Comparison of M1 and M2 for non-periodic function.

	M1				M2
δ1	m				m
1e−1	5	0.1464	0.3722	0.6772	4	0.0570	0.0194	0.1938
1e−2	20	0.0677	0.3273	0.6744	6	0.0094	0.0351	0.3741
1e−3	86	0.0343	0.3329	0.7354	14	0.0146	0.0026	0.4149
1e−4	318	0.0207	0.3663	0.9552	32	0.0063	0.0008	0.4725

Table 3. Results of high-order derivatives of Example 1.

	Second-order derivative				Third-order derivative
δ1	m				m
1e−1	6	0.0552	0.0391	43.2256	6	0.1303	0.1058	1.09e+3
1e−2	8	0.0085	0.0061	66.5999	8	0.0250	0.0195	2.08e+3
1e−3	10	0.0011	0.0011	88.3732	10	0.0038	0.0038	3.21e+3
1e−4	12	0.0001	0.0001	90.3034	12	0.0004	0.0004	3.70e+3

Example 3

8 We consider the function Let be the periodic continuation of g from the interval [0, 1] to all ℝ with period 1. Thus the original problem can be changed to find derivatives of . Since g^(k)(0) = g^(k)(1) = 0, ∀k ∈ ℕ, then . From the Corollaries 3.2 and 4.3, we have that the convergence rate of the present method is O(δ). The numerical results are shown in Table 4 and Figures 4 and 5.

We conclude the article by giving some remarks.

1.	A new method for the numerical differentiation of periodic functions is proposed and analysed. All the test numerical examples presented in the article show that the new method works well.
2.	The new method proposed in the article can be regarded as a truncated Fourier series method. The important thing is that the new operators K build a bridge between Fourier truncation method and regularization method. So we can choose a regularization parameter by a posteriori rule.

Figure 4. Results of first-order derivative of Example 3: (a) first-order derivative with δ₁ = 0.5 and (b) first-order derivative with δ₁ = 0.1.

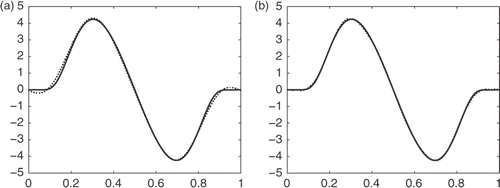
Figure 5. Results of high-order derivatives of Example 3: (a) second-order derivative with δ₁ = 0.1 and (b) third-order derivative with δ₁ = 0.1.

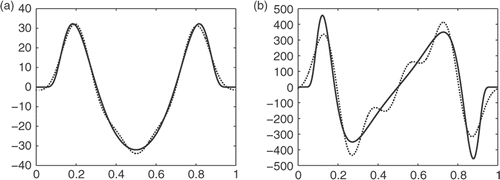
Table 4. Results of the first-order derivative of Example 3.

δ1	m
1e−1	10	0.0356	0.0415	1.5743
1e−2	12	0.0158	0.0174	6.9698
1e−3	14	0.0023	0.0039	10.2711
1e−4	20	0.0003	0.0004	13.4958

Acknowledgements

The authors are grateful to Prof. Daniel Lesnic and anonymous referees for their valuable suggestions that improved the article substantially. The project is supported by the Science Foundation of Guangdong Ocean University, No. 0812279.