A Green's function approach to Fisher information analysis and preconditioning in microwave tomography

Abstract

The Fisher Information Integral Operator (FIO) and related sensitivity analysis is formulated in a variational framework that is suitable for analytical Green's function and gradient-based approaches in microwave tomography. The main application considered here is for parameter sensitivity analysis and related preconditioning for gradient-based quasi-Newton inverse scattering algorithms. In particular, the Fisher information analysis can be used as a basic principle yielding a systematic approach to robust preconditioning, where the diagonal elements of the FIO kernel are used as targets for sensitivity equalization. The infinite-dimensional formulation has several practical advantages over the finite-dimensional Fisher Information Matrix (FIM) analysis approach. In particular, the FIO approach avoids the need of making a priori assumptions about the underlying discretization of the material such as the shape, orientation and positions of the assumed image pixels. Furthermore, the integral operator and its spectrum can be efficiently approximated by using suitable quadrature methods for numerical integration. The eigenfunctions of the integral operator, corresponding to the identifiable parameters via the significant eigenvalues and the corresponding Cramér–Rao bounds, constitute a suitable global basis for sensitivity and resolution analysis. As a generic numerical example, a two-dimensional inverse electromagnetic scattering problem is analysed and illustrates the spectral decomposition and the related resolution analysis. As an application example in microwave tomography, a simulation study has been performed to illustrate the parameter sensitivity analysis and to demonstrate the effect of the related preconditioning for gradient-based quasi-Newton inverse scattering algorithms.

Keywords:

• Fisher information analysis
• inverse scattering problems
• microwave tomography

1. Introduction

Inverse scattering problems offer many challenges in related sciences due to the ill-posedness of the reconstruction (see, e.g. 1–4). Important technical application areas include microwave tomography 5–8 and non-invasive medical imaging 9–11. In these applications, it is almost always necessary to employ some kind of regularization to stabilize the inversion algorithms and there is only a limited resolution attainable (see, for example 1,3,12–14).

The Fisher information and the Cramér–Rao bound are useful tools for resolution and sensitivity analysis in various signal estimation and imaging problems based on wave physics (e.g. 12,13,15–20). With inverse scattering problems, the Fisher information is able to connect a parameter-based description of the material and a physical model, together with some probabilistic assumption about the measurement errors. The Gaussian assumption, which is a simple yet realistic model for the measurement errors, yields a statistical bound for the estimation errors, and hence a quantitative measure on the inversion quality (see 12,13,17). In 12,13,18, the Cramér–Rao bound is employed as an analytical tool to quantify the ill-posedness of the reconstruction and to explicitly describe the inherent trade-off between the accuracy and the resolution, and in 21 the Fisher information is used in a preconditioning strategy to improve the convergence properties of a gradient-based quasi-Newton inversion algorithm.

The Fisher information analysis has mostly been given in a finite-dimensional setting (e.g. 22). One of the very few exceptions can be found in 23, where the Fisher information integral operator (FIO) for an infinite-dimensional parameter function has been employed in the estimation of wave forms (or random processes). In this article, the FIO and related sensitivity analysis is formulated in a variational framework that is suitable for analytical Green's function and gradient-based approaches in microwave tomography. A finite-dimensional Fisher Information Matrix (FIM) analysis approach for inverse scattering problems 12,13,21 is suffering from the necessity and related uncertainty of making ad hoc a priori assumptions about the underlying discretization of the material such as the shape, orientation and positions of the assumed image pixels, etc. An infinite-dimensional formulation with FIO analysis circumvents this drawback. There are two main reasons for this: (1) If analytical Green's functions can be used, these functions are defined on a continuous domain. (2) The integral operator can be efficiently discretized, e.g. by employing suitable quadrature methods for numerical integration 24 and/or Fourier series truncation. This is in contrast to employing an excessively small a priori pixel grid corresponding to a rectangular quadrature with poor numerical convergence and is hence much more preferable.

It should be noted that there is a close resemblance between the FIO analysis presented here and a SVD analysis of the corresponding linearized forward operator, i.e. a SVD analysis based on the Born approximation, the Jacobian or Fréchet derivative 𝒥, etc. (see 1,5,13,14,25,26). In fact, under the assumption that the measurement noise is an uncorrelated (white) Gaussian stochastic process and that the parameter functions belong to a pre-Hilbert space with suitable scalar products defined, these approaches can be shown to be equivalent, where the Fisher information operator is given by ℐ = 2𝒥*𝒥 and where 𝒥* is the Hilbert adjoint operator (e.g. 22) for the finite-dimensional case. The main point here is that the FIO analysis offers a statistically-based systematic approach to sensitivity analysis for inverse problems and can hence be extended, at least in principle, to include any kind of measurement noise statistics such as with arbitrary temporal and/or spatial correlations (optimal weighting of measurements with coloured noise, or optimal weighting of multi-physics data, etc.) as well as non-Gaussian noise.1 Furthermore the FIO analysis offers a quantitative measure of the parameter estimation errors in terms of the Cramér–Rao bound. Finally, and as a main application example considered in this article, the FIO analysis offers a natural basis for sensitivity analysis and preconditioning for gradient-based quasi-Newton inverse scattering algorithms. This can be motivated by the fact that the Fisher information operator (or Matrix) is given by the expected value of the Hessian of the log-likelihood function (the Hessian of the error functional) 21,22. Hence, the Fisher information analysis can be used as a basic principle yielding a systematic approach to robust preconditioning where the diagonal elements of the FIO kernel are used as targets for sensitivity equalization 21, (cf. also the Jacobi preconditioner in numerical analysis 27,28). As an example, a similar strategy can be found in 8, dealing with a two-parameter pre-scaling for Gauss–Newton image reconstruction to reduce the imbalance in the parameter sensitivity for microwave tomography. Note that the Jacobian matrix pre-multiplied by its transpose 7,8 is a FIM 21,22. Hence, the pre-conditioning presented here is similar to the reduction of multi-parameter imbalance given in 8. Note however, that the systematic feature of the Fisher information analysis presented here also implies a simultaneous reduction of the spatial imbalance of the distributed parameters. In microwave tomography, this spatial imbalance becomes significant with high contrast imaging in lossy background media using gradient-based quasi-Newton inverse scattering algorithms 6,21.

The analysis and numerical examples are concerned with two-dimensional electromagnetic inverse scattering problems based on the Helmholtz equation and related free space Green's function corresponding to a homogeneous background. For this two-dimensional problem with circular symmetry, an azimuthal Fourier series expansion is used to separate the two-dimensional eigenproblem into several one-dimensional problems, one for each Fourier component. The example problem has been chosen to be simple as well as generic and the proposed technique can thus be extended straightforwardly to deal with arbitrary background parameter profiles, provided that numerical electromagnetic solvers are employed. The two-dimensional example problem is also used to illustrate an efficient calculation of the Fisher information based preconditioning for a microwave tomography problem with circular geometry and a homogeneous lossy background, cf. 21.

The organization of this article is as follows. The FIO for inverse scattering problems is introduced in Section 2. In-depth analysis of a two-dimensional electromagnetic inverse scattering problem is treated in Section 3. Section 4 contains the numerical examples and in Section 5, the summary.

2. The FIO for inverse scattering problems

2.1. Variational formulation of the Fisher information

The FIO is a natural extension of the corresponding finite-dimensional FIM, and can hence be derived in close resemblance to the development given in 22 for example. Following the notation in 22, the symbol θ is used here to denote the unknown distributed parameter function to be estimated. In particular, let θ = θ(r) denote a real valued and piece-wise continuous parameter function, defined on a compact spatial domain Ω. Furthermore, let ξ ∈ Cⁿ denote a finite vector of complex valued sample measurements, modelled as a random vector with conditional probability density function p(ξ|θ).

To obtain the infinite-dimensional Fisher information kernel, a first order variational analysis is considered. Let δ𝒯 denote the first variation of an operator 𝒯 with respect to an incremental parameter function δθ ∈ C[Ω], where C[Ω] denotes the space of continuous functions on Ω. Hence, δ𝒯 = 𝒥δθ, where 𝒥 is the Fréchet derivative (or Jacobian) of the operator 𝒯 (see, e.g. 3). As an example, assume that the function F(h) = ln p(ξ|θ + hδθ) is differentiable in the real variable h, i.e. F(h) = F(0) + F ′(0)h + 𝒪{h²} where (·)′ denotes differentiation with respect to h and |𝒪{h²}| ≤ Ch² as h → 0. The first variation of ln p(ξ|θ) can then be calculated as δln p(ξ|θ) = F ′(0). Hence, it is straightforward to see that e.g. δ ln p(ξ|θ) = δp(ξ|θ)/p(ξ|θ). Moreover, since the Fréchet derivative 3 is a bounded linear operator, it has a representation of the form (1) where ⟨·, ·⟩ denotes a real scalar product over Ω and δ_θ(r) ln p(ξ|θ) the corresponding gradient 3, cf. also the Riesz representation theorems for bounded linear functionals 30.

Consider an unbiased estimator with (2) where ℰ{·} denotes the expectation operator with respect to the conditional probability density function p(ξ|θ). Assume that the variational and expectation operators δ and ℰ commute with the scalar products (integrals) over ξ and r, respectively. Taking the first variation of both sides of (2) yields (3) Furthermore, by employing the regularity condition ℰ{δ ln p(ξ|θ)} = ℰ{δp(ξ|θ)/p(ξ|θ)} = ∫δp(ξ|θ)dξ = δ1 = 0, it is concluded that (4)

Let a(r) ∈ C[Ω] and b(r) ∈ C[Ω] be arbitrary (test) functions, and let δθ(r) = b(r). Take the scalar product ⟨a(r), ·⟩ of both sides of (4) to obtain (5) The Cauchy–Schwarz inequality for stochastic variables 22 applied to (5) yields (6) By defining the following integral kernels: (7) (8) and the corresponding covariance and FIOs 𝒞 and ℐ (9) (10) the Cauchy–Schwarz inequality (6) finally yields (11)

2.2. Cramér–Rao bound for the principal parameters

Assume that the kernel ℐ(r′, r′′) is continuous on Ω × Ω and hence that the operator ℐ is compact and self-adjoint, with an associated discrete spectrum cf. 24. Consider the following eigenvalue problem (12) where r ∈ Ω and μ_l > 0 is a positive eigenvalue, ϑ_l (r) ∈ C[Ω] the corresponding normalized eigenfunction and l a countable index. Similar to the Karhunen–Loève expansion of a stochastic process 23, the principal parameters η_l and the corresponding unbiased estimator are defined here by (13) (14) By choosing a(r) = ϑ_l (r) and in (11) and by noting that , the Cramér–Rao bound for the principal parameters are given by (15)

2.3. The Gaussian measurement model

The results in Sections 2.1 and 2.2 are valid for general stochastic measurement models p(ξ|θ). Next, explicit results will be given that are related to finite stochastic measurements with Gaussian distribution. Hence, let (·)^T and (·)^H denote the transpose and the conjugate transpose, respectively, and consider the following Gaussian measurement model (16) where ξ ∈ Cⁿ is the complex measurement vector, ψ(θ) ∈ Cⁿ a complex vector valued functional of the real function θ(r) and N ∈ Cⁿ a complex Gaussian random vector with zero mean and covariance matrix ℰ{NN ^H} = R (see, e.g. 22). Hence, the probability density function p(ξ|θ) for the measurement vector is given by (17) By employing the correlation properties of the complex Gaussian vector 22, i.e. ℰ{(ξ − ψ(θ))(ξ − ψ(θ))^H} = R and ℰ{(ξ − ψ(θ))(ξ − ψ(θ))^T} = 0, it is straightforward to show that (8) becomes (cf. also 22). (18)

2.4. Measurements over a frequency interval

The results in Section 2.3 are now generalized to include measurements over an interval in the frequency domain, under the assumption of additive Gaussian measurement noise. Consider the following statistical measurement model regarding a single spatial measurement point: (19) where ξ(t) is the real time-domain stochastic measurement process, ψ(t, θ) the physical observation model, N(t) the noise and T the length of the observation interval. The noise is assumed to be sampled from a real Gaussian stochastic process with zero mean, correlation function r_N(τ) = ℰ{N(t + τ)N(t)} and power spectral density where f denotes the frequency. The correlation function is assumed to have finite support within some fixed interval [−T₀/2, T₀/2] where T₀ ≤ T. The complex Hilbert pair, or analytic signal2 corresponding to (19) is given by (20) where Ñ(t) is zero mean complex Gaussian noise with power spectral density where u(f) is the Heaviside unit step function (cf. 22,31,32).

Next, the stochastic processes in (19) and (20) are regarded to be periodic processes, where the correlation function r_N(τ) has period T 23,33. A discrete measurement model is then obtained from a Fourier series representation of (20) (21) where the Fourier coefficients are . The noise terms Ñ_p are zero mean complex Gaussian3 with covariance function where (·)* denotes the complex conjugate and δ_pq the Kronecker delta (see, e.g. 23). From (18) and (21), it is now concluded that (22) as T → ∞, and where the relations and have been used. Here ψ(f, θ) denotes the Fourier transform of ψ(t, θ). Since ψ(t, θ) is real and ψ(−f, θ) = ψ*(f, θ), the Fisher information integral kernel is finally given by (23) Note that the Fourier transform of a stationary stochastic process is an uncorrelated (white noise) process with infinite variance and correlation function ℰ{N(f)N*(f ′)} = R(f)δ(f − f ′) where δ(·) denotes the Dirac delta function, see e.g. 33. Hence, the limiting process above is formal and the integral (23) should be understood in the sense of a Lebesgue–Stieltjes integral 23,34.

2.5. Fisher information and the SVD of the forward operator

It is a close connection between the FIO analysis based on (22) and (23), and an SVD analysis of the corresponding linearized forward operator. To see this connection, let 𝒥 denote the Fréchet derivative (or Jacobian) of the forward operator ψ(f, θ) where (see, e.g. 1,3,5) (24) Further, define the scalar product ⟨·, ·⟩₁ for measurements ξ(f) and η(f) as (25) where R_N(f) is the power spectral density employed in (22) and (23). The adjoint operator 𝒥* is given by (26) where ⟨𝒥δθ, ξ⟩₁ = ⟨δθ, 𝒥*ξ⟩ (see, e.g. 3,24).

A maximum likelihood (ML) estimation criterion 23 based on the same limiting process as described in Section 2.4 above leads to the error functional , where the norm is based on the scalar product given in (25) above. The first- and second-order variations of F are given by δF = ⟨δθ, g⟩ = ⟨δθ, 2𝒥*(ψ(f, θ)−ξ)⟩ and δ²F = ⟨δθ, Hδθ⟩ = ⟨δθ, 2𝒥*𝒥δθ⟩ + 2⟨δ²ψ(f, θ), ψ(f, θ) − ξ⟩₁, where g = 2𝒥*(ψ(f, θ) − ξ) denotes the gradient and H the Hessian, respectively. The Fisher information operator defined by (22) or (23) can now be identified as the self-adjoint operator (27) and where ℐ = ℰ{H } (see also 22 for the finite-dimensional case).

In conclusion, under the assumption of Gaussian noise with power spectral density R_N(f), an eigenspace analysis of the Fisher information ℐ = 2𝒥*𝒥 is equivalent to performing an SVD analysis 3 of the linearized forward operator 𝒥 based on the scalar product (25). This interpretation facilitates an appropriate, statistically optimum spectral weighting of the measurement data. For multiple measurements, the scalar product in (25) can be straightforwardly extended by using a summation over all measurement configurations.

3. Two-dimensional inverse scattering problem

Consider the two-dimensional electromagnetic inverse scattering problem of imaging an isotropic circular cylinder of radius a in a homogeneous and isotropic background space (Figure 1). Let (ρ, φ, z) denote the cylindrical coordinates, the corresponding unit vectors and the two-dimensional radius vector with coordinates (ρ, φ). Let ε(ρ) denote the unknown relative permittivity function to be estimated, defined on the compact two-dimensional spatial domain Ω = {ρ|ρ ≤ a} where a > 0 (Figure 1).

Figure 1. Two-dimensional inverse scattering problem with a relative permittivity function ε(ρ) over a cylinder ρ ≤ a. Measurement cylinder of radius b > a with excitation at (b, ϕ) and measurement at (b, φ). The background space is homogeneous and isotropic with ε(ρ) = ε for ρ > a.

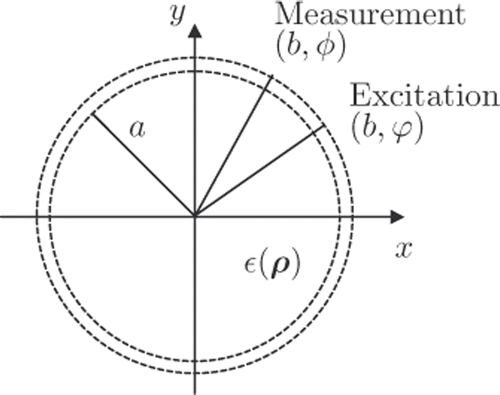
Both the excitation (line) source J and hence the electric field E are assumed to be linearly polarized with and , and both fields depend on the two-dimensional spatial domain ρ ∈ R². The measurement is performed on a cylinder of radius b > a with near-field excitation at (b, ϕ) and measurement at (b, φ). As will be shown below, the condition b > a implies continuity of the Fisher information integral kernel, and hence compactness of the corresponding integral operator (cf. Section 2.2). The inverse problem consists of estimating the relative permittivity function ε(ρ) within the cylindrical object for ρ ≤ a, based on measurements (or observations) of the electric field ψ(φ, ϕ, t) = ψ(ρ, t) at ρ = b, i.e. for (φ, ϕ, t) ∈ [0, 2π] × [0, 2π] × [−T/2, T/2] where T is the length of the observation interval. Here, ε(ρ) is the relative permittivity within the cylinder, and ϵ its value outside. Hence, ε(ρ) = ε for ρ > a.

In the frequency domain, the Maxwell's equations yield the following wave equation for the scalar field ψ, i.e. the Helmholtz equation in cylindrical coordinates (28) where k = ω/c is the wave number, ω = 2π f the angular frequency with the time convention e^iωt, c the speed of wave propagation in free space and η the wave impedance of free space. The corresponding Green's function G(ρ, ρ′) = G(ρ, φ, ρ′, φ′) for a line source at ρ′ = (ρ′, φ′) satisfies {∇² + k²ε(ρ)}G(ρ, ρ′) = −δ(ρ − ρ′) where δ(·) is the spatial impulse or Dirac delta function.

For a homogeneous background with ε(ρ) = ε, the background Green's function is given by (29) where J_m(·) and are the Bessel function and the Hankel function of the second kind, respectively, both of order m (see e.g. 35). Here, ρ_< = min{ρ, ρ′} and ρ_> = max{ρ, ρ′}. Assuming that the source is a line source at ρ′ with J(ρ) = S(f)δ(ρ − ρ′), the solution to (28) is given by (30) where S(f) is the Fourier transform of the excitation signal. Hence, in the frequency domain, the observed field is given by ψ(φ, ϕ, f) = ψ(ρ, f)|_ρ=b = −ikηS(f)G(b, φ, b, ϕ). Further, let the two-dimensional Fourier coefficients of the 2π × 2π periodic function ψ(φ, ϕ, f) be defined by (31) where ψ(φ, ϕ, f) is the Fourier transform of ψ(φ, ϕ, t). For the homogeneous background, it then follows from (29) that .

3.1. Measurements over frequency and space

The results in Section 2.4 are now generalized to include measurements over the spatial region [0, 2π] × [0, 2π], under the assumption of additive Gaussian measurement noise. Consider the following statistical measurement model for the space and time domain (32) for (φ, ϕ, t) ∈ [0, 2π] × [0, 2π] × [−T/2, T/2], which is a two-dimensional extension of the (single spatial point) measurement model in (19), and where the argument θ in ψ(φ, ϕ, t) has been suppressed for simplicity. The measurement signal ψ(φ, ϕ, t) is assumed to be real and the noise N(φ, ϕ, t) is assumed to be sampled from a spatially uncorrelated real Gaussian stochastic process with zero mean and correlation function (33) where δ(·) denotes an impulse function with period 2π. Here, r_N(τ) denotes the temporal correlation function with power spectral density , as defined in Section 2.4. The complex time-domain Hilbert pair corresponding to (32) is given by (34) where Ñ(φ, ϕ, t) is a zero mean complex Gaussian stochastic process with the corresponding temporal power spectral density . A discrete measurement model is obtained by assuming that the stochastic process in (32) is periodic with period 2π × 2π × T, and considering the corresponding temporal-spatial Fourier series representation (35) where the Fourier series coefficients are given by (36) Following the arguments in Section 2.4, it is straightforward to show that the noise terms Ñ_mnp are zero mean complex Gaussian distributed with covariance function (37) Hence, from (18) with δ_θ(r) = δ_θ(ρ), and the model (35), it follows that (38) as T → ∞, where the integral is a Lebesgue–Stieltjes integral as in (23) above, and where the relations and have been used. Since ψ(φ, ϕ, t) is real and , the Fisher information integral kernel is finally given by (39)

3.2. Gradients and Fisher information

To obtain the gradient used in (39), a first-order perturbation analysis is considered in (28) where ε(ρ) → ε(ρ) + hδε(ρ) and ψ(ρ) → ψ(ρ) + hδψ(ρ) + 𝒪(h²) where δε(ρ) ∈ C[Ω] and ‖𝒪(h²)‖ ≤ Ch² as h → 0. The resulting non-homogeneous wave equation for the first variation δψ(ρ) is (40) where ψ(ρ) is the solution to (28). The solution to (40) is given by (41) and the corresponding gradient is obtained as (42)

Since the excitation is a line source at (b, ϕ) and ψ(ρ′) = −ikηS(f)G(ρ′, φ′, b, ϕ) as given by (30), the gradient of the observed field ψ(φ, ϕ, f) is (43) where the symmetry G(ρ, ρ′) = G(ρ′, ρ) of the Green's function has been employed.

For a homogeneous background with ε(ρ) = ε, the two-dimensional Fourier series representation of (43) follows by applying (29). Hence, (44)

Assuming that the parameter function ε(ρ) is real valued, the Fisher information in (39) can now be expressed as (45)

Next, suppose that the noise power spectral density and the excitation is constant over the relevant bandwidth, i.e. R_N(f) = N₀ and ωS(f) = ω₀S(f₀), respectively, for ω ∈ ω₀[1 − B/2, 1 + B/2], where ω₀ is the centre frequency and B the normalized bandwidth. Further, let ν = ω/ω₀ = f/f₀ = k/k₀ denote the normalized frequency variable, and define the dimensionless signal to noise ratio SNR by (46) The Fisher information in (45) can then be expressed as (47) For simplicity, we choose SNR = 1 in the following. It is also convenient to consider the Fisher information with respect to the dimensionless spatial variable ρ ↔ k₀ρ, given by (48) where the corresponding dimensionless eigenvalues and eigenfunctions are and , respectively, and where μ_l and ϑ_l (ρ) are defined in (12). Note that the singularity of the Green's function in (43) is avoided since ρ′, ρ′′ ≤ a < b, and the kernel defined in (48) is therefore continuous. Hence, the operator ℐ is compact and self-adjoint (cf. 24).

3.3. Dispersive material models and parameter scaling

An application for the Fisher information analysis is with sensitivity analysis and preconditioning for inverse scattering problems (see, e.g. 21,36). Here, it is important to treat dispersive material models involving complex valued parameters. A generic example is given by the complex permittivity (49) where ϵ_r, α, τ₀ and β are dimensionless real valued parameters of a combined Debye and conductivity model. The sensitivity of the parameter θ ∈ {ϵ_r, α, β} is given by (50) where , P_α(ν) = 1/(1 + iντ₀) and P_β = 1/iν and where is given by (44). By employing that θ is real and hence (51) the Fisher information for the parameter θ is obtained from (39), (44) and (50) as (52) where the dimensionless spatial variable (ρ ↔ k₀ρ) has been used and where SNR = 1.

Of particular interest is the diagonal of this integral kernel, which is given here by (53) and which depends only on the radial coordinate ρ due to the circular symmetry. A preconditioner that is suitable for gradient-based quasi-Newton inversion algorithms is obtained by scaling the parameters such that the new parameter functions have uniform sensitivity in the sense of the diagonal Fisher information corresponding to some known background 21. Hence, a suitable scaling is given here by (54) where the parameter θ₀ corresponds to the known background. The scaling, the gradients and the new Fisher information are hence given by (55) respectively. Note that uniformly over ρ ∈ Ω as well as over θ ∈ {ε_r, α, β} when θ corresponds to the known background parameter θ₀.

3.4. The eigenvalue problem

For simplicity, the case with ε = 1 is treated below. The general case with complex ε can be treated similarly. Due to the circular symmetry and a reorganization of the double summation, the Fisher information in (48) can be expressed as (56) where φ = φ′ − φ′′, and where the Fourier series coefficients in (56) are given by (57) Note that the Fourier series coefficients ℐ_q(ρ′, ρ′′) are real and symmetric, i.e. ℐ_−q(ρ′, ρ′′) = ℐ_q(ρ′, ρ′′).

The eigenvalue problem in (12) can now be stated as (58) or, equivalently, as the following Fourier series representation: (59) where −∞ < q < ∞, and (60)

Let q be an arbitrary integer, and let ϑ_lq(ρ) be an eigenfunction of (59) with eigenvalue μ_l. Then ϑ_l (ρ, φ) = ϑ_lq(ρ)e^iqφ is an eigenfunction of (58) with the same eigenvalue μ_l. Since the integral operator ℐ defined by (58) is compact and self-adjoint, the eigenspace corresponding to any particular eigenvalue μ_l is finite dimensional 24, and hence the Fourier series representation in (60) is finite (where the summation limits depend on l).

For q = 0, eigenvalues μ_l and eigenfunctions are generated, where are the corresponding real eigenfunction solutions of (59). Since the Fisher information is real with ℐ_−q(ρ′, ρ′′) = ℐ_q(ρ′, ρ′′), any pair (q, −q) with q ≥ 1 will generate (at least) two linearly independent eigenfunctions ϑ_lq(ρ)e^iqφ and ϑ_l,−q(ρ)e^−iqφ sharing the same eigenvalue μ_l. Real eigenfunctions (corresponding to the real parameter function θ(ρ, φ)) satisfying the conjugate symmetry are obtained as (61) where are the real eigenfunction solutions of (59) for q ≥ 1. The set of all eigenvalues and eigenfunctions of (58) may be obtained as the union of all the eigenvalues and eigenfunctions generated by (59) for −∞ < q < ∞, counted with multiplicity.

To solve the eigenvalue problem (58) numerically, let the Fourier series in (56) be truncated with |q| ≤ Q. Any suitable quadrature method for one-dimensional numerical integration 24 can now be used to approximate (59) using a finite-dimensional matrix formulation given by (62) where _q is an N × N matrix, an N × 1 vector and N is the number of quadrature points.

4. Numerical examples

4.1. A comparison between the finite- and infinite-dimensional Fisher information analysis techniques

The Fisher information analysis presented in 12,13,21 is based on a finite-dimensional presumption. However, there are no contradictions between the FIM and FIO approaches. They are consistent. As an example, by comparing the two-dimensional expressions for the Fisher information given in 13,28 with the present results, it is observed that the expressions (4.2) and (4.5) in 21 for small pixel sizes correspond asymptotically to the uniformly sampled FIO kernels given above in (52). The Fisher information analysis presented in 13,21 is of course still valid. However, the present infinite-dimensional formulation provides a simplified asymptotic analysis (as ka → ∞) and more general results since no a priori assumptions have to be made about the pixel positions, shape and orientation, etc. As an example, in the evaluation of the Fisher information which is presented in Figure 6 in 21, a deviation can be observed between the FIM and FIO techniques, as illustrated in Figure 2.

Figure 2. Radial Fisher information for the parameter ε_r corresponding to a lossy background with relative permittivity , ε_r = 78 and β = 3.6. The solid line shows the FIO technique (53) and the dashed lines the FIM technique for the varying pixel sizes d = {0.13, 0.26, 0.40, 0.53} as shown in Figure 6 in 21. All plots have been normalized to a maximum of 0 dB. Here, the size of the cylinder is a = 0.1 m, the centre frequency f₀ = 1 GHz and the relative bandwidth B = 1.

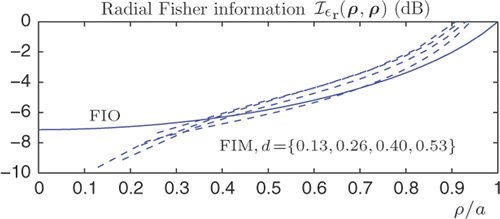
In particular, the FIM calculation in 13,21 is based on circularly symmetrical pixels with equal area and radially varying shape, and shows a large deviation (under-estimation of the ‘true’ Fisher information) close to the centre of the object, i.e. in a region where the assumed pixels become excessively thin and ‘needle’-like. Note that this ‘artifact’ is not an error, and it has no significant impact on the qualitative results of 13,21. The advantage of the FIO technique is, however, that it is able to yield the sensitivity for the whole domain, with no regard to any a priori assumed pixel shapes.

4.2. Two-dimensional inverse scattering problem

Consider the two-dimensional electromagnetic inverse scattering problem described in Section 3. For simplicity, the case with ε = 1 is treated below. The general case with complex ϵ can be treated similarly. The dimensionless Fisher information is defined in (48) and decomposed in a Fourier series in (56) and (57). The spectral properties of the corresponding integral operator defined by (58) is investigated below. A numerical scheme is used here where (57) is truncated with |q| ≤ Q and |m| ≤ 2Q. The simple, and frequently used composite Simpson's rule 24 is employed to approximate the one-dimensional integral operators in (59), yielding the finite-dimensional eigenvalue problems stated in (62). In the numerical examples below, the Fourier series truncation is set to Q = 40, the number of radial quadrature points is N = 31, and hence there is a total of 2511 eigenvalues (counting multiplicity). The measurement cylinder radius is b = 1.1a.

Consider the narrowband case B → 0, which is easily accounted for by putting ν = 1, dν = B and neglecting the integral over ν in (57). Let λ₀ denote the wavelength and k₀ = 2π/λ₀, the wave number. The eigenvalues of the integral operator in (58) is shown in Figure 3 for k₀a = 2π{1, 2, 4, 8}. Figure 3(a) shows the eigenvalues in decreasing order (counting multiplicity). Note that the resolution limit is given here approximately by the sharp ‘knee’, or ‘threshold’, at which the eigenvalues starts to drop off in exponential decay.

Figure 3. (a) Eigenvalues μ_l as a function of index (counting multiplicity) corresponding to the Fisher information kernel for a two-dimensional circular domain. (b) Eigenvalues μ_l as a function of resolution limit in fractions of the wavelength λ₀. Here, B = 0 (narrowband case) and k₀a = 2π{1, 2, 4, 8}.

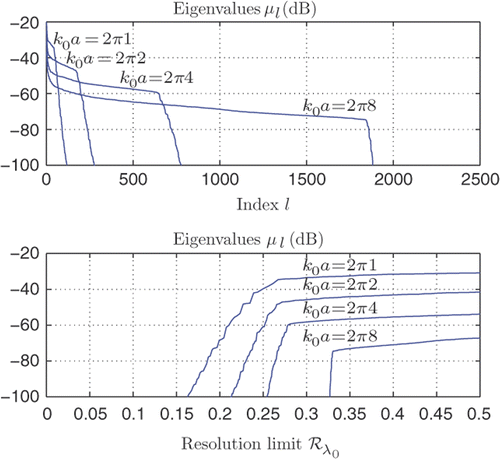
The resolution limit may be further quantified as follows. A dimensionless measure of the cylinder cross-section area is and the corresponding resolution limit based on l useful eigenfunctions is defined by (63) in dimensionless fractions of the wavelength λ₀. Figure 3(b) shows the eigenvalues μ_l as a function of the resolution limit defined in (63).

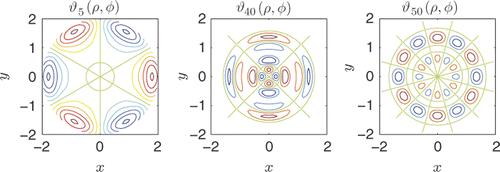
In Figure 4 a selection of useful eigenfunctions with various spatial variability, chosen within the resolution limit for k₀a = 2π2 is shown. It is concluded from Figure 3 that a resolution limit of corresponds approximately to l = 180 eigenfunctions.

Figure 4. A selection of useful eigenfunctions ϑ_l (ρ, φ) with l = {5, 40, 50} within the resolution limit (l = 180) for k₀a = 2π2, corresponding to the Fisher information operator for a two-dimensional circular domain. The cartesian x and y axes shown are normalized to the wavelength and the radius of the circular domain is a = 2λ₀.

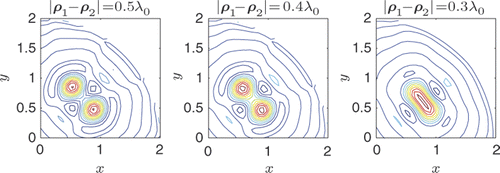
To demonstrate the actual resolution capability versus the predicted , an eigenfunction expansion of two closely spaced impulse functions δ(ρ − ρ₁) + δ(ρ − ρ₂) is carried out. In Figure 5 is shown an expansion using the first 180 eigenfunctions. The distance between the impulses is d = |ρ₁ − ρ₂| = λ₀{0.5, 0.4, 0.3}. This eigenfunction expansion may be used to quantify the minimum resolvable distance between two small and closely spaced objects. The numerical example verifies the rather coarse definition (63) with reasonable precision.

Figure 5. Eigenfunction expansion of two closely spaced impulse functions δ(ρ − ρ₁) + δ(ρ − ρ₂) using the eigenfunctions ϑ_l (ρ, φ) for l = 1, … , 180, corresponding approximately to the resolution limit for k₀a = 2π2. The distance between the impulses are |ρ₁ − ρ₂| = λ₀{0.5, 0.4, 0.3}. The cartesian x and y axes shown are normalized to the wavelength and the radius of the circular domain is a = 2λ₀.

4.3. Application example in microwave tomography

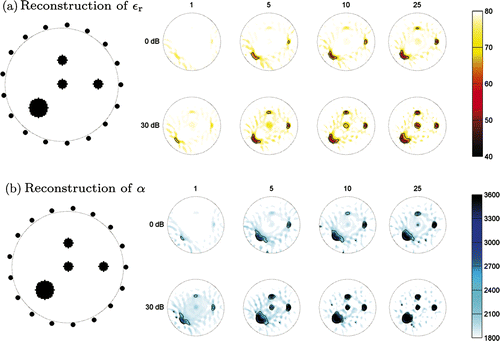
As an application example, the Fisher information operator is employed as a tool to perform parameter sensitivity analysis and preconditioning for gradient-based inverse scattering algorithms. The basic ideas have been briefly outlined in Section 3.3, and can be used in microwave tomography 21. A two-dimensional microwave tomography set-up is considered here as in 21, consisting of 17 antennas placed on a circle of radius a = 0.1 m (Figure 6). The computer simulation and inversion algorithm is based on an FDTD electromagnetic solver and a time-domain least-squares optimization approach based on the conjugate-gradient algorithm, as described in 6,7,37,38. The synthetic data is generated using a 1 mm calculation grid and noise is added corresponding to a signal to noise ratio of 60 dB. The reconstructions are performed using a 2 mm grid.

Figure 6. Reconstruction results for (a) ε_r and (b) α, corresponding to a background with ε_r = 80, α = 1800 and τ₀ = 100. To the left is shown the antenna positions and the simulated true values of ε_r and α, respectively. To the right is shown the reconstruction results for iteration 1, 5, 10, 25 without (0 dB) and with (30 dB) the radial gradient scaling (55) incorporated, respectively.

The centre frequency is chosen to f₀ = 1 GHz corresponding to k₀a = 2.1 and the bandwidth f_B = 1 GHz, and hence B = 1. The following Debye model is considered (64) where the background parameters are ε_r = 80, α = 1800 and τ₀ = 100. With this choice of background parameters, the wavelength at f = 1.5 GHz is λ = 22 mm. It is noted that with this choice of parameters, ε is very close to a conductivty model ε = ε_r + β/iν where β = σ/ω₀ε₀ and σ = 1 Sm⁻¹. These model parameters have been chosen mainly to illustrate the importance of proper parameter scaling when relatively high losses are present, such as with salty water (ε_r ∼ 80 and σ ∼ 1 Sm⁻¹). In Figure 6 is shown the simulated true values of the relative permittivity ε_r and the Debye parameter α. The scatterer consists of four cylindrical objects, one object with radius 16 mm and three objects with radius 8 mm which are all modelled with ε_r = 40 and α = 3600. The reconstruction algorithm has furthermore been designed to include a simple threshold, maintaining the a priori information that ε_r ≤ 80 and α ≥ 1800.

The Fisher information corresponding to the background parameters is calculated according to (53), and is shown in Figure 7 for 10 log SNR = 100 dB. In Figure 7 is also shown the Fisher information for the parameter α₁ according to the alternative model (65) where α₁ = α/τ₀. As can be seen in Figure 7, this simple intuitive choice of parameter scaling results in very similar sensitivity for the two parameters ε_r and α₁. Note however, that the parameter scaling given by (54) and (55) is a systematic approach to performing sensitivity equalization not only between different parameters as ε_r and α, but also with regard to the spatial domain Ω.

Figure 7. Radial Fisher information corresponding to the background with ε_r = 80, α = 1800 and τ₀ = 100. The relative bandwidth is B = 1 and k₀a = 2.1. The solid line shows , dashed line and dash-dotted line ℐ_α.

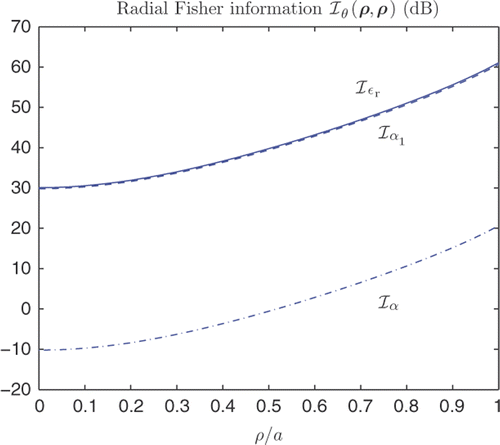
The reconstruction results are illustrated in Figure 6, without (0 dB) and with (30 dB) the radial gradient scaling (55) incorporated, respectively. Note that the radial dynamics of the Fisher infomation for all the three parameters ε_r, α and α₁ is about 30 dB in this example (cf. Figure 7). The example illustrates the importance of employing proper parameter scaling and preconditioning for gradient-based quasi-Newton optimization approaches, in particular with high contrast imaging when losses are relatively high (see also 21).

5. Summary

The FIO has been defined by using a variational formulation, with a specific application to inverse scattering problems and microwave tomography. In particular, the derivation yields a gradient-based formulation which is useful in connection with analytical Green's function techniques. The spectral decomposition of this compact and self-adjoint operator contains all the essential information about the invertability and the resolution limit for a weak scattering inverse problem. The analysis can be performed without having to resort to any particular assumptions about the shape, orientation and positions of discrete image pixels, etc., as with the finite-dimensional FIM analysis approach. It has been illustrated how the integral kernel can be calculated explicitely for a two-dimensional inverse scattering problem, and that the related eigenvalue problem can be solved efficiently by using suitable quadrature methods for numerical integration. As an application example in microwave tomography, a simulation study has been performed to illustrate the parameter sensitivity analysis and to demonstrate the effect of the related preconditioning for gradient-based quasi-Newton inverse scattering algorithms.

Acknowledgements

The research leading to these results has received funding from the European Union's Seventh Framework Programme (FP7/2007–2013) under grant agreement no. 225663. The work has also been supported by the Swedish Research Council as well as the Swedish Foundation for Strategic Research within the Strategic Research Center Charmant.

Notes

Notes

1. A realistic example is the generalized normal distribution 27 with exponential parameter p ≥ 1 where the exponent p = 1 corresponds to the Laplacian density, p = 2 to the Gaussian density and p = ∞ to the uniform density, etc. Basic expressions for the corresponding FIM are given in 27.

2. The analytic time-domain signal is , where denotes the Hilbert transform (see, e.g. 32).

3. Note that the Fourier series representation of a real Gaussian process is not necessarily complex Gaussian (cf. 22,23,31).